Теория игр. Позиционные игры. Антагонистические позиционные игры. Нормализация позиционной игры. Позиционные игры с полной информацией. Критерии принятия решений с помощью дерева решений. Безусловный денежный эквивалент игры. Средний выигрыш. Ожидаемая денежная оценка. Ожидаемая ценность точной информации
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Теория игр
Лекция
4
Тема
лекции 4: «Позиционные игры»

Разделы лекции:
1. Антагонистические позиционные игры.
Нормализация позиционной игры.
2. Позиционные игры с полной
информацией.
3. Критерии принятия решений с помощью
дерева решений.

РАЗДЕЛ 1. АНТАГОНИСТИЧЕСКИЕ ПОЗИЦИОННЫЕ
ИГРЫ. НОРМАЛИЗАЦИЯ ПОЗИЦИОННОЙ ИГРЫ.
КАКАЯ
ИГРА НАЗЫВАЕТСЯ ПОЗИЦИОННОЙ ИГРОЙ?
Во многих практически важных
конфликтных ситуациях стороны-участницы, располагая той или иной информацией о
прошлом развитии конфликта, совершают свой выбор не раз и навсегда, а
последовательно во времени, шаг за шагом. Тем самым, они используют стратегии,
отражающие как динамику конфликта, так и степень собственной информированности
о фактически складывающейся обстановке в развитии этого конфликта.
Одним
из классов игр, описывающих конфликты, динамика
которых оказывает влияние на поведение участников, являются так
называемые позиционные игры.
ПОЗИЦИОННАЯ
ИГРА — ЭТО БЕСКОАЛИЦИОННАЯ ИГРА,
МОДЕЛИРУЮЩАЯ ПРОЦЕССЫ ПОСЛЕДОВАТЕЛЬНОГО ПРИНЯТИЯ РЕШЕНИЙ ИГРОКАМИ В
УСЛОВИЯХ МЕНЯЮЩЕЙСЯ ВО ВРЕМЕНИ И, ВООБЩЕ ГОВОРЯ, НЕПОЛНОЙ ИНФОРМАЦИИ.
Процесс
самой игры состоит в последовательном переходе от одного состояния игры к
другому состоянию, который
осуществляется либо путем выбора игроками одного из возможных действий в
соответствии с правилами игры, либо случайным образом (случайный ход). В
качестве примеров позиционных игр можно привести крестики-нолики, шашки, шахматы, карточные
игры, домино и др. Интересно, что право выбора первого хода в этих играх
часто определяется случайным образом.
СОСТОЯНИЯ
ИГРЫ ПРИНЯТО НАЗЫВАТЬ ПОЗИЦИЯМИ (ОТСЮДА И НАЗВАНИЕ — ПОЗИЦИОННЫЕ ИГРЫ), А
ВОЗМОЖНЫЕ ВЫБОРЫ В КАЖДОЙ ПОЗИЦИИ — АЛЬТЕРНАТИВАМИ.
ЧТО
ТАКОЕ ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПОЗИЦИОННОЙ ИГРЫ?
В
исследовании позиционной игры большую пользу приносит наглядное графическое
изображение конкретной позиционной игры в виде так называемого дерева игры.
ЧТО
ТАКОЕ ДЕРЕВО ИГРЫ?
Характерной
особенностью позиционной игры является возможность
представления множества позиций в виде древовидного упорядоченного множества,
которое называется деревом игры
(рисунок
1).








1 2 1 2 1 2 1 2





1 2
1 2

1 2
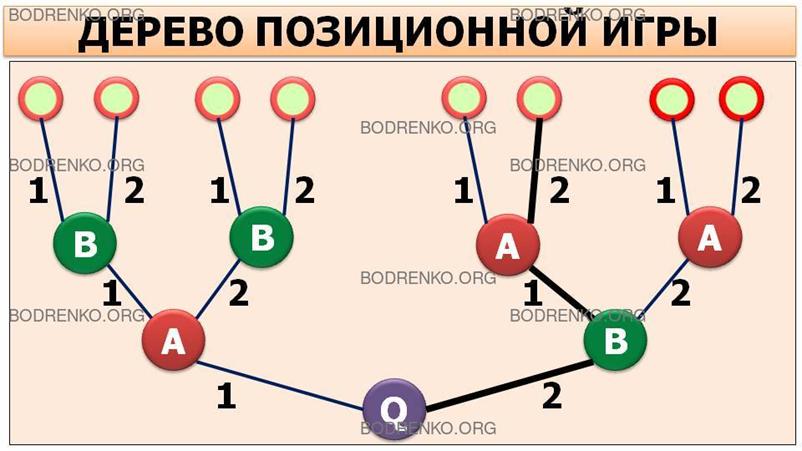
Рисунок 1. Дерево позиционной игры.
Если говорить более подробно, то деревом позиционной игры называется плоская фигура, состоящая из узлов и конечного числа направленных вверх прямолинейных отрезков, соединяющих эти узлы; каждый узел обозначается цифрой (или другим символом), соответствующей номеру игрока, делающего ход, и изображает ход этого игрока, поэтому каждому ходу соответствует набор узлов, расположенных на одном определенном уровне. На самом низшем уровне имеется только один узел — основание дерева (начальная вершина), каждый узел соединяется только с одним узлом на низшем уровне, каждый прямолинейный отрезок означает выбор, сделанный игроком на данном ходе, и обозначается номером, соответствующим сделанному выбору. Если в игре используется ход, осуществляемый не игроком, а случайным механизмом (иногда его называют «ПРИРОДОЙ»), то обычно узлу, соответствующему данному ходу, присваивается номер 0 (нуль) или, например, символ Q (как на рисунке 1). Окончательными вершинами дерева (окончательными позициями) являются окончания прямолинейных отрезков, исходящих из узлов последнего уровня. Ветвью дерева называется ломаная линия, состоящая из прямолинейных отрезков дерева, которая начинается в самом нижнем узле (начальная вершина) и идет вверх последовательно через соответствующие узлы до окончательной вершины дерева.
ЗАМЕЧАНИЕ. Например, в позиционной игре,
представленной на рисунке 1 своим деревом, первый ход производится случайно (символ
Q).
Символы Q,
А или B
в кружке указывают, кто из игроков (Q, А или В) делает очередной ход в
данной позиции.
КАК
ГРАФИЧЕСКИ ИЗОБРАЖАЕТСЯ ПАРТИЯ ПОЗИЦИОННОЙ ИГРЫ?
Пользуясь
графическим описанием игры в виде дерева игры, можно заметить, что процесс игры
состоит в переходе от начальной позиции (начальная вершина) к окончательной позиции (окончательная
вершина), через непосредственно следующие одна за другой промежуточные позиции.
Каждая
окончательная вершина определяет
единственную цепь (последовательность идущих друг за другом звеньев),
связывающую начальную вершину с
данной (окончательной вершиной) (рисунок 1). Такая
цепь (то есть ветвь дерева) называется партией. На рисунке 1 одна из партий выделена жирными линиями. Число различных партий равно числу
окончательных вершин (позиций). В каждой окончательной позиции задан числовой
выигрыш игрока А.
Используя
понятие ветви дерева игры, можно
сказать, что каждая ветвь дерева игры изображает партию игры.
Например,
в шахматах функция выигрышей игрока A (белых) определяется так:
(+1)
на выигрываемых партиях,
0
на ничейных партиях,
(-1)
на проигрываемых партиях.
Функция
выигрышей игрока B (черных) отличается от
функции выигрышей игрока A (белых) только знаком.
ЗАМЕЧАНИЕ.
Позиционная
игра может быть представлена графически в виде дерева, которое дает наглядное
представление об игре. С другой стороны, графическое представление игры,
выполненное с соблюдением правил его построения, дает основание для формального
представления позиционной игры, и можно рассматривать теоретически не сами
позиционные игры, а их графическое представление в виде дерева.
РАЗЛИЧАЮТ ПОЗИЦИОННЫЕ ИГРЫ С ПОЛНОЙ
ИНФОРМАЦИЕЙ И ПОЗИЦИОННЫЕ ИГРЫ С
НЕПОЛНОЙ ИНФОРМАЦИЕЙ.
В позиционных играх с полной
информацией
(пример — шашки, шахматы) каждый игрок
при своем ходе знает ту позицию дереза
игры, в которой он находится.
В позиционных играх с неполной информацией (пример — домино) игрок, делающий ход, не знает точно, в какой именно позиции дерева игры он фактически находится. Этому игроку известно лишь некоторое множество позиций, включающее в себя его фактическую позицию. Такое множество позиций называется информационным множеством. Позиции, принадлежащие одному и тому же информационному множеству, объединяются пунктирными линиями. В каждое информационное множество входят только неразличимые для игрока узлы, т. е. только те узлы, для каждой пары из которых соответствующий игрок не может точно указать, в какой точке дерева он находится, делая этот ход.
Составляя
информационные множества, следует помнить следующее:
(а) в одно информационное множество
могут входить только узлы, относящиеся к одному игроку;
(б) любая линия игры (ветвь дерева,
отображающая партию игры) не должна пересекать одно и то же информационное
множество больше одного раза.
Условие
(б) можно сформулировать еще так: в одно информационное множество не должно
входить больше одного узла каждой ветви, отображающей партию игры.
ЧТО
ТАКОЕ ПОЗИЦИОННАЯ ИГРА С ИДЕАЛЬНОЙ ПАМЯТЬЮ?
Игры
с идеальной памятью являются интересным обобщением игр с полной информацией. Игрой
с идеальной памятью называется игра, в которой каждый из игроков всегда помнит
все, что он делал или знал во время каждого из своих ходов. Например, всякая
игра двух игроков, в которой могут играть лишь два человека (а не команда),
способные помнить всю информацию о выборах в любом ходе, является игрой с
идеальной памятью.
Используя
понятие информационного множества, игру с идеальной памятью можно определить
более точно.
Позиционная
игра — это игра с идеальной памятью, если для нее выполняются следующие
условия.
Пусть
Χ и Υ — любые два хода,
выполняемые одним игроком и такие, что в некоторой партии игры ход Χ предшествует ходу Υ;
-
U и V — информационные множества, содержащие соответственно Χ и Υ;
-
каждая точка информационного множества U дает k альтернатив;
-
Ui (i = 1, 2, ..., k) — множество всех узлов
дерева (ходов), которые можно достигнуть, выбрав i-ю альтернативу в некоторой точке
множества U,
тогда
для любого i имеет место соотношение: информационное множество V содержится во
множестве Ui.
ПРИМЕРЫ
АНТАГОНИСТИЧЕСКИХ ПОЗИЦИОННЫХ ИГР.
Ниже
мы рассмотрим два примера позиционных игр, в каждой позиции которых, кроме
окончательных позиций, ровно две
альтернативы — первая и вторая; игры в этих двух примерах (примеры 1, 2)
будут состоять из двух ходов, которые
последовательно делают участвующие в ней игроки A и B. Начинает игрок A: он выбирает одну из двух
возможных альтернатив — число x, равное
либо 1 (первая альтернатива), либо 2 (вторая альтернатива). На ход игрока A игрок B отвечает своим ходом, выбирая одну из двух возможных альтернатив —
число y, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива). В результате игрок A получает вознаграждение или вынужден
платить штраф.
ПРИМЕР 1.
1-й
ход. Игрок A выбирает число x из множества двух чисел {1,2}.
2-й
ход. Игрок B выбирает число y из множества двух чисел {1,2}, зная
выбор числа x игроком А.

Функция
W(x,
у) выплат игроку A за счет игрока B задается так:
W(1,1) = 10;
W(2,1) = -20;
W(1,2) = -10;
W(2,2) = 20.

На
рисунке 2 показаны дерево игры и информационные множества для примера 1.
1 -1 -2 2





 1 2 1 2
1 2 1 2


 1 2
1 2

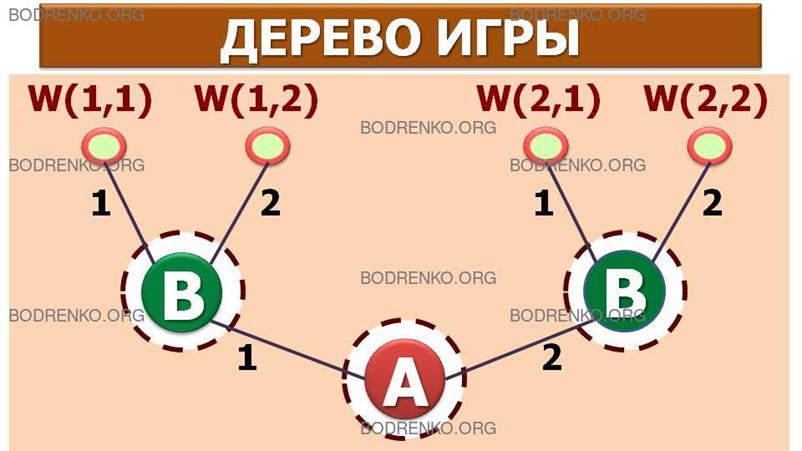
Рисунок 2. Дерево позиционной игры.
ПРИМЕР 2. В случае, когда выполнены все условия предыдущего примера 1,
кроме одного — игрок B на 2-м ходе выбирает число y из множества двух чисел {1,2}, не зная
выбора числа x игроком A, — информационные множества выглядят
так, как показано на рисунке 3.
10 -10 -20 20




1
2 1 2

1 2


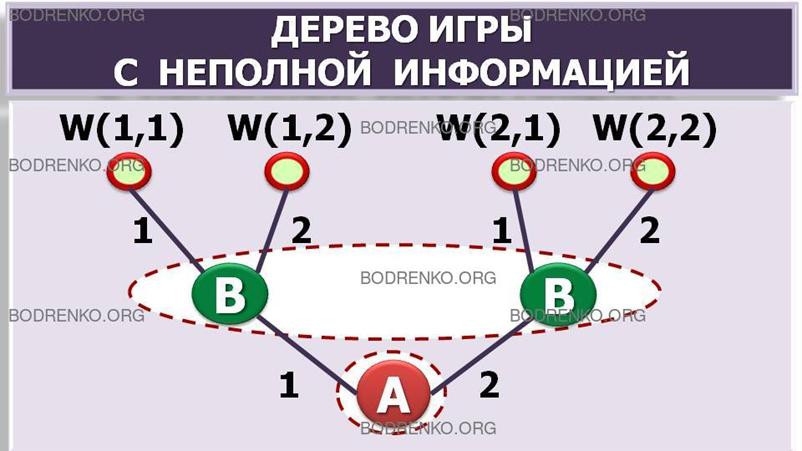
Рисунок 3. Дерево позиционной игры.
Это
игра с неполной информацией: игрок B при своем ходе знает, в каком
информационном множестве он находится, но ему неизвестно, в какой именно
позиции этого множества — левой или правой.
НОРМАЛИЗАЦИЯ ПОЗИЦИОННОЙ ИГРЫ.
Заранее
определенную последовательность ходов игрока,
выбранную им в зависимости от информации о ходах другого игрока и ходах
игрока Q
(«ПРИРОДЫ»), будем называть чистой стратегией
этого игрока. В том случае, если в игре нет случайных ходов (игрок Q в игре не участвует), выбор игроком A и игроком B чистых стратегий однозначно определяет исход игры — приводит к
окончательной позиции, где игрок A и получает свой выигрыш. Это
обстоятельство позволяет сводить позиционную игру к матричной игре.
В
ЧЕМ ЗАКЛЮЧАЕТСЯ НОРМАЛИЗАЦИЯ ПОЗИЦИОННОЙ ИГРЫ?
ПРОЦЕСС
СВЕДЕНИЯ АНТАГОНИСТИЧЕСКОЙ ПОЗИЦИОННОЙ ИГРЫ К МАТРИЧНОЙ ИГРЕ НАЗЫВАЕТСЯ
НОРМАЛИЗАЦИЕЙ ПОЗИЦИОННОЙ ИГРЫ.
Покажем
на нескольких примерах, как это делается.
ПРИМЕР
1 (ПРОДОЛЖЕНИЕ).
Опишем
стратегии игроков.
Стратегию
игрока A
можно задать одним числом x, показывающим, какую альтернативу, первую или вторую, выбрал
игрок.
Тем
самым, у игрока A две чистых стратегии:
Α1
— «выбрать x = 1»,
A2
— «выбрать x = 2».
Стратегию
игрока B
(принимая во внимание, что выбор игрока A на 1-м ходе ему известен) удобно
описывать упорядоченной парой [y1, y2].
Здесь
y1 (y1 = 1,2) — альтернатива, выбираемая игроком B при условии, что игрок A выбрал первую альтернативу (x = 1),
а
y2 (y2 = 1,2) — альтернатива, выбираемая
игроком B
при условии, что игрок A выбрал вторую альтернативу (x = 2).
Например,
выбор игроком B стратегии [2,1] означает, что если на
1-м ходе игрок A выбрал x = 1, то игрок B на своем ходе должен выбрать у = 2.
Если
же на 1-м ходе игрок A выбрал x = 2, то согласно этой стратегии игрок B на своем ходе должен выбрать у = 1.
Таким образом, у игрока B четыре чистых стратегии:
B1
— [1,1] («у = 1 при любом выборе x»);
B2 — [1,2] («у = x при любом выборе «x»);
B3 — [2,1] («у ≠ x при любом выборе «x»);
B4
— [2,2] («у = 2 при любом выборе «x»).

Покажем
теперь, как рассчитываются выигрыши игрока A в зависимости от примененных
стратегий.
Пусть,
например, игрок A выбрал стратегию А1 — (1), а игрок В —
стратегию В2 — [1,2]. Тогда x = 1, а из стратегии [1,2] вытекает,
что у = 1. Отсюда
W(x, y)
= W(1,1) = 10.
Остальные
выигрыши рассчитываются совершенно аналогично.
Результаты
расчетов записываются обычно или в виде таблицы
выигрышей игрока A (таблица 1)
Таблица
1.
|
Игрок B Игрок A |
B1 [1,1] |
B2 [1,2] |
B3 [2,1] |
B4 [2,2] |
|
A1 (x=1) |
W(1,1) |
W(1,1) |
W(1,2) |
W(1,2) |
|
A2 (x=2) |
W(2,1) |
W(2,2) |
W(2,1) |
W(2,2) |

или
в виде матрицы игры:
|
10 |
10 |
-10 (*) |
-10 |
|
-20 |
20 |
-20 |
20 |

где,
как обычно, строки соответствуют стратегиям игрока A, а столбцы — стратегиям игрока В. Полученная матрица имеет седловую точку,
которая отмечена (*).
Оптимальные
стратегии игроков: Α1 — (x=1) и B3 — [2,1]. Тем самым, игрок A на 1-м ходе выбирает x = 1, а игрок B на 2-м ходе выбирает у = 2. Цена игры
ν = -10.
ПРИМЕР
2 (ПРОДОЛЖЕНИЕ). Опишем стратегии игроков.
У
игрока A
они те же, что и в предыдущем примере 1:
Α1
— «выбрать x = 1»,
А2
— «выбрать x = 2».
Так
как игроку B
выбор игрока A
неизвестен,
то есть игрок B не знает, в какой именно из двух
позиций он находится (см. рис. 3), то у него те же две стратегии:
Β1
— «выбрать у = 1»,
В2
— «выбрать у = 2».

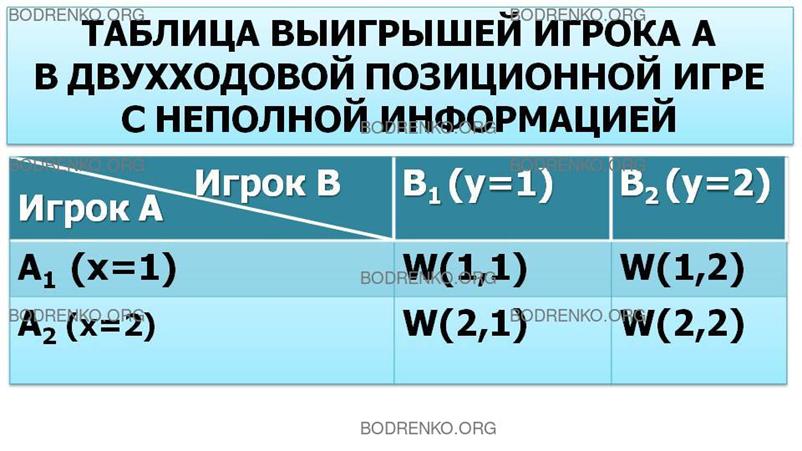
Таблица
выигрышей игрока A имеет следующий вид (таблица 2):
Таблица
2.
|
Игрок B Игрок A |
B1 (y=1) |
B2 (y=2) |
|
A1 (x=1) |
W(1,1) |
W(1,2) |
|
A2 (x=2) |
W(2,1) |
W(2,2) |
Матрица
игры имеет следующий вид:
|
10 |
-10 |
|
-20 |
20 |

Полученная
матрица седловой точки не имеет.
Оптимальные
смешанные стратегии игроков следующие.
S1 – оптимальная смешанная стратегия
игрока A:
|
A1 |
A2 |
|
2/3 |
1/3 |
S2 – оптимальная смешанная стратегия
игрока B:
|
B1 |
B2 |
|
1/2 |
1/2 |
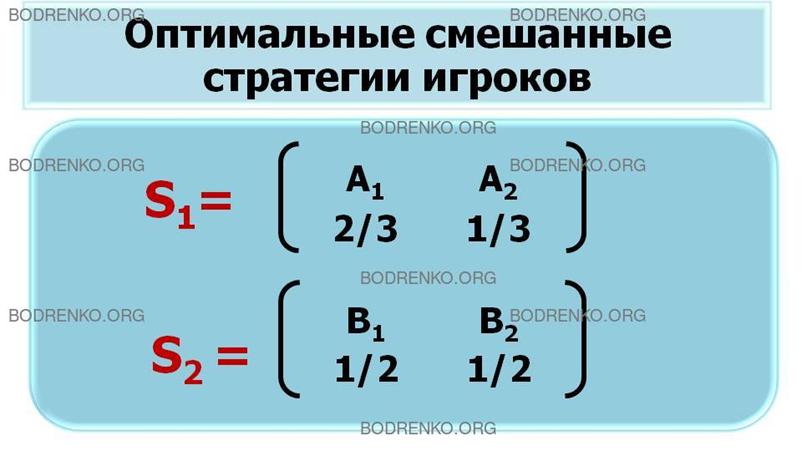
Цена
игры ν = 0.
ЗАМЕЧАНИЕ. На этих двух примерах хорошо видно,
что результат сведения позиционной игры к матричной игре напрямую зависит от
степени информированности игроков. В
частности, отсутствие у игрока B сведений о выборе, сделанном игроком A, приводит к уменьшению количества его
возможных стратегий.
РАЗДЕЛ 2. ПОЗИЦИОННЫЕ ИГРЫ С ПОЛНОЙ
ИНФОРМАЦИЕЙ.
КАКАЯ
ПОЗИЦИОННАЯ ИГРА НАЗЫВАЕТСЯ ИГРОЙ С ПОЛНОЙ ИНФОРМАЦИЕЙ?
Позиционная
игра называется игрой с полной информацией, если в каждой позиции любой ее
партии игрок, делающий ход, знает, какие
альтернативы были выбраны на предыдущих ходах. В графическом описании каждая вершина дерева
такой игры представляет собой отдельное информационное множество. Примерами
позиционных игр с полной информацией могут служить крестики-нолики,
шашки и шахматы.
В
ЧЕМ ЗАКЛЮЧАЕТСЯ ОСНОВНАЯ ОСОБЕННОСТЬ АНТАГОНИСТИЧЕСКОЙ ПОЗИЦИОННОЙ ИГРЫ С
ПОЛНОЙ ИНФОРМАЦИЕЙ?
Основная
особенность антагонистической позиционной игры с полной информацией состоит в том, что
соответствующая ей матрица выигрышей всегда имеет седловую точку, то есть в
игре с полной информацией существуют оптимальные чистые стратегии и, значит,
равновесная ситуация.
Сказанное
означает, что в шахматах (крестиках-ноликах, шашках) уже в начальной позиции
либо имеется способ выигрыша за белых, либо способ выигрыша за черных, либо как
та, так и другая сторона способна форсировать ничью. Однако известное доказательство существования равновесной
ситуации неконструктивно и не дает эффективных приемов фактического
нахождения решения игры в общем случае.
Иное дело с игрой крестики-нолики: стратегий в ней немного и она разобрана до
самого конца — существуют оптимальные
чистые стратегии, ведущие игроков к ничьей.
Рассмотрим
несколько примеров позиционных игр с полной информацией.
1.
Как нетрудно заметить, двухходовая игра из примера 1 является игрой с полной
информацией. Ее нормализация приводит к матрице с седловой точкой (пример 1).
2.
«Выкладывание монет на стол». Два игрока поочередно кладут монеты одинаковых размеров на обыкновенный стол,
всякий раз выбирая произвольное
доступное место для монеты (взаимное накрывание монет не допускается).
Тот из игроков, кто положит монету, не оставляющую места для новых монет, выигрывает. Это игра с полной информацией.
Существует вполне определенная
стратегия, обеспечивающая выигрыш тому из игроков, кто начинает
игру: начинающий игру должен положить
первую монету точно в центр стола и на каждый ход противника отвечать
симметричным ходом. Исход игры от стратегии
второго игрока не зависит.
ПРИМЕР 3. «ПЕРЕГОВОРЫ».
В
переговорах участвуют две стороны A и B. В слегка идеализированном варианте это может
выглядеть, например, так. Сначала сторона A высказывает одно из нескольких
предложений, способных заинтересовать
сторону B.
Затем сторона B, ознакомившись с предложением стороны A, высказывает одно из нескольких
встречных предложений, способных, по ее
мнению, заинтересовать сторону A. В свою очередь, сторона A, ознакомившись с реакцией стороны B на сделанные предложения, высказывает
ей новое предложение, внеся одну из нескольких возможных корректировок в свое первоначальное
предложение с учетом мнения стороны B и т. д. Если предмет переговоров
сложен, то подобный обмен ходов может
затянуться. Однако любые переговоры непременно заканчиваются. И там, на
финише, ждет функция выигрышей.
Попробуем
смоделировать короткий переговорный процесс при помощи трехходовой позиционной
игры. Предположим, что переговоры
заканчиваются через три хода, на каждом из которых соответствующая
сторона имеет возможность выбора из двух альтернатив, и опишем
соответствующую позиционную игру.
1-й
ход делает сторона A: она выбирает одно из двух
возможных предложений — число x из множества двух чисел {1,2}.
2-й
ход делает сторона B: она выбирает число у из множества
двух чисел {1,2}, зная число х, предложенное стороной A.
3-й
ход делает сторона A: она выбирает число z из множества двух чисел {1,2}, зная о предложении стороны B на 2-м ходе и помня собственное
предложение на 1-м ходе.

После
этого сторона A либо получает вознаграждение
(например, в виде кредита от стороны В), либо выплачивает стороне B штраф. Все эти возможности описываются
функцией выигрышей W(x, у, z),
заданной следующей таблицей.
W (1,1,1) = a;
W (1,1,2) = b;
W (1,2,1) = c;
W (1,2,2) = d;
W (2,1,1) = e;
W (2,1,2) = f;
W (2,2,1) = g;
W (2,2,2) = h.

Ясно,
что описанная позиционная игра является игрой с полной информацией.
Графическое
представление этой игры показано на рисунке 4. Сделаем необходимые пояснения к
данному рисунку. Поскольку первый ход делает первый игрок (сторона A), то самый нижний узел
соответствует ходу первого игрока (сторона A) и обозначен буквой A. Из этого узла исходят
два отрезка (ветви), соответствующие выбору 1 или 2, которые обозначены
соответственно цифрами 1 и 2. Второй ход делает второй игрок (сторона B), поэтому узлы второго уровня обозначены буквой B. Поскольку второму игроку известен выбор
первого игрока на первом ходе, то второй
игрок (сторона B), делая свой ход, знает, в
каком месте дерева (на какой ветви дерева) находится. Если первый игрок (сторона
A), на первом ходе выбрал
число 1, то второй игрок (сторона B) находится на левой ветви
дерева, если же первый игрок (сторона A) на первом ходе выбрал число 2, второй (сторона B) находится на правой ветви дерева. Таким образом, левый узел с буквой
B образует
отдельное информационное множество. Аналогично и правый узел с буквой B также образует информационное
множество. Поскольку третий ход делает первый игрок (сторона A), то третий уровень узлов обозначен
буквой A.
Первый игрок, делая третий ход, помнит о своем выборе на первом ходе, и
поэтому он знает, на какой ветви дерева находится второй игрок, делая второй
ход. Далее, так как первому игроку
известен выбор второго игрока, то он точно знает, в каком месте дерева сам
находится, делая выбор на третьем ходе. Поэтому каждый узел третьего уровня
образует отдельное информационное множество. Каждая партия игры представляется
на дереве в виде отдельной ветви, которая идет от самого нижнего узла через
один узел каждого
уровня и заканчивается одной верхней точкой. Всего может быть восемь
возможных партий (по количеству самых верхних точек). Любая партия игры
характеризуется точкой, координата которой соответствует выбору определенного
игрока. Всего может быть 8 точек:
(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2). Каждой
точке соответствует выигрыш первого игрока согласно функции W (х, у, z). Так как часто над каждой верхней
точкой проставляют выигрыш первого игрока в соответствующей партии, то для
рассматриваемой игры получим рисунок 4.
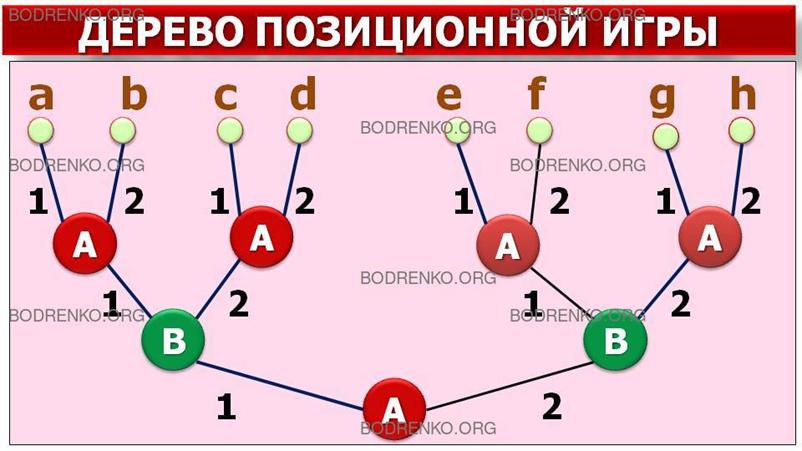
Рисунок 4. Дерево позиционной игры.
Для
нормализации этой позиционной игры сначала опишем возможные стратегии игрока B. Поскольку игроку B выбор игрока A на 1-м ходе известен, то у игрока B те же четыре стратегии, что и в
примере 1:
Таким
образом, у игрока B четыре чистых стратегии:
B1
— [1,1] («у = 1 при любом выборе x»);
B2 — [1,2] («у = x при любом выборе «x»);
B3 — [2,1] («у ≠ x при любом выборе «x»);
B4
— [2,2] («у = 2 при любом выборе «x»).

Другими
словами, у второго игрока столько стратегий, сколько имеется способов
отображения множества {1, 2} в себя.
С
описанием возможных стратегий игрока A дело обстоит немного посложнее — их восемь. Стратегия для первого
игрока должна учитывать результаты сделанных ранее выборов. При каждом выборе
на первом ходе может быть два выбора на втором ходе, т. е. уже имеется четыре
варианта, а при каждом из этих вариантов может быть сделано два выбора, т. е. всего
8 возможных стратегий. Обозначим через (i, [i1, i2])
стратегию первого игрока. Число i (i = 1,2) означает выбор первым игроком
на первом ходе; i1 (i1 = 1,2) - выбор первым игроком на
третьем ходе, если второй игрок на втором ходе выбрал число 1; i2 (i2 = 1,2) — выбор первым игроком на
третьем ходе, если второй игрок на втором ходе выбрал число 2.
Таким образом, чистая стратегия игрока A в данной игре описывается упорядоченной тройкой (i, [i1, i2]).
A1: (1, [1,1]); A2: (1, [1,2]); A3: (1, [2,1]); A4: (1, [2,2]);
A5: (2, [1,1]); A6: (2, [1,2]); A7: (2, [2,1]); A8: (2, [2,2]).

Например,
стратегия A3: (1, [2, 1]) означает следующую
стратегию первого игрока: на первом ходе он выбирает число 1 (первая цифра в
скобках), а на третьем ходе он выбирает число 2, стоящее на втором месте в
скобках, если второй игрок на втором ходе выбрал число 1; если же второй игрок
на втором ходе выбрал число 2, то первый игрок на третьем ходе должен выбрать
число 1, стоящее на третьем месте в скобках. Выигрыши первого игрока
определяются так. Пусть, например, первый
игрок применяет стратегию A3:
(1, [2, 1]), а второй — первую стратегию B1:
[1,1]. Тогда
из из стратегии A3: (1, [2, 1]) следует, что х= 1,
далее, второй игрок, невзирая на х, выбирает у = 1, а из стратегии A3: (1,[2, 1]) следует, что первый игрок
выдаст z
= 2. Получим выигрыш W (х, у, z) = W (1, 1, 2) = b.
Аналогично
рассчитываются остальные выигрыши. Теперь приведем матрицу выигрышей первого
игрока (игрок A) в зависимости от применяемых
стратегий (таблица 3), где столбцы соответствуют стратегиям второго игрока (игрок
B),
а строки — стратегиям первого игрока (игрок A).
Другими словами, составляем матрицу выигрышей первого игрока (игрок A) в матричной игре двух игроков с
нулевой суммой (таблица 3).
Таблица
3.
|
ИГРОК B ИГРОК
A |
B1: [1,1] |
B2: [1,2] |
B3: [2,1] |
B4: [2, 2] |
|
A1: (1,[1,1]) |
W(1,1,1) |
W(1,1,1) |
W(1,2,1) |
W(1,2,1) |
|
A2: (1,[1,2]) |
W(1,1,1) |
W(1,1,1) |
W(1,2,2) |
W(1,2,2) |
|
A3: (1,[2,1]) |
W(1,1,2) |
W(1,1,2) |
W(1,2,1) |
W(1,2,1) |
|
A4: (1,[2,2]) |
W(1,1,2) |
W(1,1,2) |
W(1,2,2) |
W(1,2,2) |
|
A5: (2,[1,1]) |
W(2,1,1) |
W(2,2,1) |
W(2,1,1) |
W(2,2,1) |
|
A6: (2,[1,2]) |
W(2,1,1) |
W(2,2,2) |
W(2,1,1) |
W(2,2,2) |
|
A7: (2,[2,1]) |
W(2,1,2) |
W(2,2,1) |
W(2,1,2) |
W(2,2,1) |
|
A8: (2,[2,2]) |
W(2,1,2) |
W(2,2,2) |
W(2,1,2) |
W(2,2,2) |
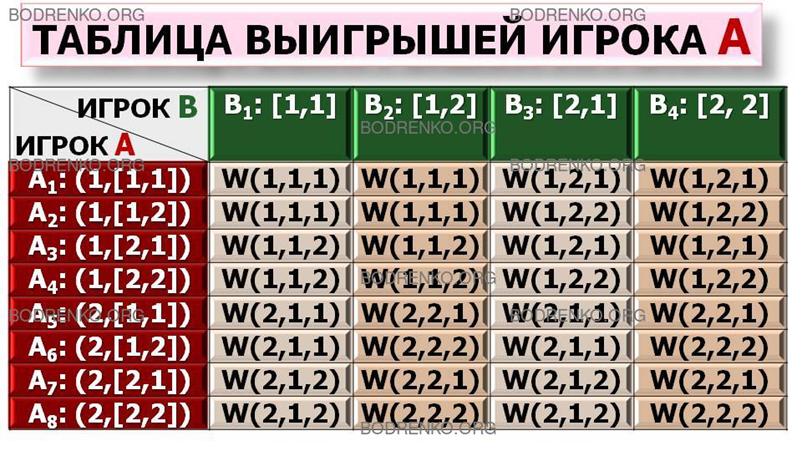
Вследствие
того, что рассматриваемая позиционная игра является игрой с полной информацией,
полученная матрица имеет седловую точку при любой функции выигрышей.
|
a |
a |
c |
c |
|
a |
a |
d |
d |
|
b |
b |
c |
c |
|
b |
b |
d |
d |
|
e |
g |
e |
g |
|
e |
h |
e |
h |
|
f |
g |
f |
g |
|
f |
h |
f |
h |
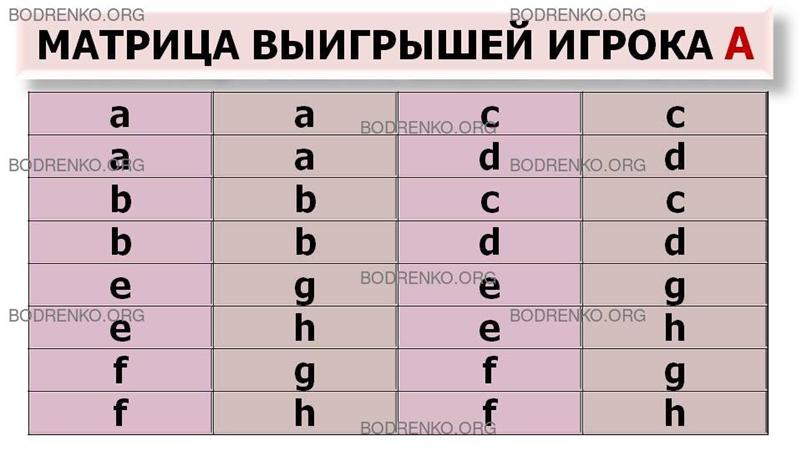
В
этом легко убедиться, задавая произвольно значения параметров a, b, c, d, e, f, g, h.
Пусть,
например, функция W(х, у, z) задана следующим образом:
W (1,1,1) = -2; W (1,1,2) = -1; W (1,2,1) = 3; W (1,2,2) = -4; W (2,1,1) =5; W (2,1,2) = 1;
W
(2,2,1) = 2; W (2,2,2) = 6.

Тогда
получим следующую матрицу выигрышей игрока A.
|
-2 |
-2 |
3 |
3 |
|
-2 |
-2 |
-4 |
-4 |
|
-1 |
-1 |
3 |
3 |
|
-1 |
-1 |
-4 |
-4 |
|
5 |
2 |
5 |
2 |
|
5 (*) |
6 |
5 (*) |
6 |
|
1 |
2 |
1 |
2 |
|
1 |
6 |
1 |
6 |
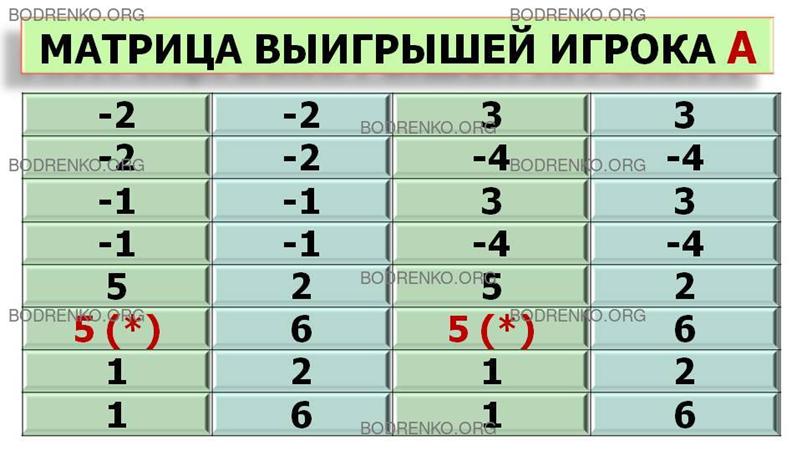
Исследуя
эту игру обычными способами, приходим к решению: имеется две седловые точки,
отмеченные звездочкой в платежной матрице игрока A. Оптимальная стратегия первого игрока A6: (2, [1, 2]) состоит в выборе числа х
= 2 на первом ходе и числа z — на третьем ходе, равного числу у, выбранного
вторым игроком на втором ходе. У второго игрока имеется две оптимальные
стратегии: первая и третья. То есть выбирать число у = 1, невзирая на х, или
выбирать число у, отличное от х: y≠ x. Цена игры равна 5.
Рассмотрим
некоторую интерпретацию этой игры. Например, имеются две страны, которые хотят
установить между собой деловые связи. Они должны решить вопрос о строительстве
завода. Первая страна может построить завод для второй страны. Эту ситуацию
упрощенно представим в виде следующей позиционной игры.
Ход
1. Первая страна (первый игрок A) делает выбор из двух альтернатив: 1-я
— предложить второй стране построить завод для производства автомобилей, 2-я —
построить завод для переработки сельскохозяйственной продукции.
Ход
2. Вторая страна (второй игрок B), зная, какую альтернативу выбрала
первая страна на первом ходу, делает выбор из двух альтернатив: 1-я — строить
завод по производству автомобилей и предложить это первой стране, 2-я — строить
завод по переработке сельскохозяйственной продукции и предложить это первой
стране.
Ход
3. Первая страна, зная выбор второй страны на втором ходу и помня свой выбор на
первом ходу, делает выбор из двух альтернатив: 1-я—согласиться с предложением
второй страны, 2-я — не согласиться с ним. После того, как сделаны все три
хода, первая страна получает сумму W (х, у, z), где х выбор 1 или 2 на
первом ходу, у — выбор 1 или 2 на втором ходу, z — выбор 1 или 2 на третьем
ходу. Функция W (х, у, z) совпадает с функцией,
определенной в игре примера 3.
При
увеличении числа ходов стратегии в позиционной игре с полной информацией строятся по аналогичной
схеме.
В
рассмотренных примерах основное внимание было уделено описанию процесса нормализации позиционной
игры — построению дерева игры и информационных множеств, выработке стратегий
игроков и вычислению элементов платежной матрицы. Следующий естественный шаг — отыскание
цены игры и оптимальных стратегий
игроков — проводится методами, о которых рассказывалось в лекции 2, посвященной
антагонистическим играм.
Мы
достаточно подробно остановились на позиционных играх двух лиц, где были явно
выражены интересы одного из игроков (игрока А). Следует, однако, иметь в виду,
что в одних случаях интересы игрока B могут быть полностью
противоположными интересам игрока А, в
то время как в других вполне может оказаться, что то, что хорошо для одного
игрока, не обязательно плохо для другого.
РАЗДЕЛ 3. КРИТЕРИИ ПРИНЯТИЯ РЕШЕНИЙ С
ПОМОЩЬЮ ДЕРЕВА РЕШЕНИЙ.
Приведенные
выше примеры не исчерпывают всех возможных вариантов даже в этом, самом
простом, случае двухходовых позиционных игр. Рассмотрим более сложные
(позиционные, или многоэтапные) решения в условиях риска. Одноэтапные игры с
природой, таблицы решений, удобно использовать в задачах, имеющих одно
множество альтернативных решений и одно множество состояний среды. Многие
задачи, однако, требуют анализа последовательности решений и состояний среды,
когда одна совокупность стратегий игрока и состояний природы порождает другое
состояние подобного типа. Если имеются два (или более) последовательных
множества решений, причем последующие решения основываются на результатах
предыдущих, и/или два (или более) множества состояний среды (т.е. появляется
целая цепочка решений, вытекающих одно из другого, которые соответствуют
событиям, происходящим с некоторой вероятностью), используется дерево решений.
КАКОЙ СМЫСЛ ИМЕЕТ ТЕРМИН «ДЕРЕВО
РЕШЕНИЙ»?
Дерево решений — это графическое изображение последовательности
решений и состояний
среды с указанием соответствующих вероятностей и выигрышей
для любых комбинаций альтернатив и состояний среды.
В постановочном плане рассмотрим несколько задач, которые
могут быть решены с помощью данного метода.
ЗАДАЧА 1. РАЗВЕДЫВАТЕЛЬНОЕ БУРЕНИЕ
СКВАЖИН.
Некоторая нефтяная разведывательная партия должна решить,
стоит ли бурить скважины на данном участке до того, как истечет срок контракта.
Для руководителей партии не ясны многие обстоятельства:
- в какую сумму обойдется стоимость бурения, зависящая от
качества грунта, глубины залегания нефти и т.д.;
- на какие запасы
нефти в этом месте можно рассчитывать;
- сколько
будет стоить эксплуатация скважины.
В распоряжении руководства имеются объективные данные об
аналогичных и не вполне похожих скважинах этого типа. При помощи сейсмической разведки можно получить
дополнительную информацию, которая, однако, не дает исчерпывающих сведений о
геофизической структуре разведываемого участка. Кроме того, получение сейсмической
информации стоит недешево, поэтому еще до того, как будет принято окончательное
решение (бурить или нет), следует определить, есть ли необходимость собирать
эти сведения.
ЗАДАЧА 2. ВЫПУСК НОВОГО ТОВАРА.
Большая химическая компания успешно завершила исследования
по усовершенствованию строительной краски. Руководство компании должно решить,
производить эту краску самим (и если - да, то какой мощности строить завод)
либо продать патент или лицензию, а также технологию независимой фирме,
которая имеет дело исключительно с производством и сбытом строительной краски.
Основные источники неопределенности следующие:
- рынок
сбыта, который фирма может обеспечить при продаже новой краски по данной цене;
- расходы на
рекламу, если компания будет сама производить и продавать краску;
- время, которое потребуется конкурентам, чтобы выпустить на
рынок подобный товар (успеет ли компания за этот срок окупить затраты,
понесенные для того, чтобы стать лидером в данной сфере производства).
Компания может получить некоторые дополнительные сведения,
имеющие косвенное отношение к проблемам проникновения конкурентов на рынок
сбыта, опросив часть поставщиков краски. Но к материалам опросов следует относиться
с осторожностью, ибо поставщики в действительности могут поступать не так, как
они первоначально предполагают. В качестве подтверждения последнего суждения
можно привести исследования, проведенные
американскими автомобильными корпорациями для того, чтобы определить спрос на
большие легковые автомобили. Несмотря на надвигающийся энергетический кризис
1971-1973 гг., результаты анкетирования показали, что американские покупатели
по-прежнему предпочитают многоместные легковые автомобили. Однако на деле все
произошло с точностью до «наоборот», и на рынке стали пользоваться спросом
небольшие, экономичные машины. Такие результаты опроса могут быть частично
объяснены скрытностью человеческого характера, и это должно учитываться при
принятии решений.
КАКОВЫ ОСНОВНЫЕ ЭТАПЫ АНАЛИЗА И РЕШЕНИЯ
ЗАДАЧ С ПОМОЩЬЮ ДЕРЕВА РЕШЕНИЙ?
Процесс принятия решений с помощью дерева решений в общем
случае предполагает выполнение следующих пяти этапов.
ЭТАП 1. Формулирование
задачи. Прежде всего, необходимо отбросить не относящиеся к проблеме
факторы, а среди множества оставшихся факторов выделить существенные и несущественные.
Это позволит привести описание задачи принятия решения к поддающейся анализу
форме.
На данном этапе должны быть выполнены следующие основные процедуры:
- определение возможностей сбора информаций для
экспериментирования и реальных действий;
- составление перечня событий, которые с определенной
вероятностью могут произойти;
- установление временного порядка расположения событий, в
исходах которых содержится полезная и доступная информация, и тех
последовательных действий, которые можно предпринять.
ЭТАП 2. Построение дерева решений.
ЭТАП 3. Оценка
вероятностей состояний среды, т.е. сопоставление шансов возникновения
каждого конкретного события. Следует отметить, что указанные вероятности
определяются либо на основании имеющейся статистики, либо экспертным путем.
ЭТАП 4. Установление
выигрышей
(или проигрышей, как выигрышей со
знаком минус) для каждой возможной комбинации альтернатив (действий) и
состояний среды.
ЭТАП 5. Решение задачи.
РЕШЕНИЕ ИГРОВЫХ ЗАДАЧ С ПОМОЩЬЮ ДЕРЕВА РЕШЕНИЙ.
Прежде чем продемонстрировать процедуру применения дерева
решений, введем ряд определений.
В зависимости от отношения к риску решение задачи может выполняться
с позиций так называемых «объективистов»
и «субъективистов». Поясним эти
понятия на следующем примере.
ПРИМЕР. Пусть предлагается лотерея: за 100
рублей (стоимость лотерейного билета)
игрок с равной вероятностью p
= 0,5
может ничего не выиграть или выиграть 1000 рублей. Один индивид пожалеет и 100
рублей за право участия в такой лотерее, то есть просто не купит лотерейный
билет; другой индивид готов заплатить
за лотерейный билет 500 рублей; а третий заплатит даже 600 рублей за
возможность получить 1000 рублей (например, когда ситуация складывается так,
что, только имея 1000 рублей, игрок может достичь своей цели, поэтому возможная
потеря последних денежных средств, а у него их ровно 600 рублей, не меняет для
него ситуации).
ЧТО ТАКОЕ ОЖИДАЕМАЯ ДЕНЕЖНАЯ ОЦЕНКА ИГРЫ?
Ожидаемая
денежная оценка (ОДО)
игры рассчитывается как сумма
произведений размеров выигрышей на вероятности этих выигрышей.
Например, для нашей лотереи ОДО = 0,5*0 + 0,5*1000 = 500
рублей.
ЧТО ТАКОЕ БЕЗУСЛОВНЫЙ ДЕНЕЖНЫЙ ЭКВИВАЛЕНТ ИГРЫ?
Безусловным
денежным эквивалентом (БДЭ) игры называется максимальная сумма денег, которую ЛПР готов
заплатить за участие в игре (лотерее), или (что то же) та минимальная сумма
денег, за которую он готов отказаться от игры. Каждый индивид имеет свой БДЭ.

КОГО УСЛОВНО НАЗЫВАЮТ «ОБЪЕКТИВИСТОМ»
ИЛИ «СУБЪЕКТИВИСТОМ»?
«Объективистом» условно называют индивида, для которого безусловный денежный эквивалент (БДЭ) игры
совпадает с ожидаемой денежной оценкой
(ОДО) игры, то есть со средним выигрышем в игре (лотерее). То есть для
«объективиста» БДЕ = ОДО.
«Субъективистом» условно называют индивида, для которого БДЭ ≠ ОДО. Если «субъективист» склонен к риску, то
его БДЭ > ОДО. Если «субъективист»
не склонен к риску, то его БДЭ < ОДО.
Предположим, что решения принимаются с позиции объективиста.
И рассмотрим процедуру принятия решения на примере следующей задачи.
ЗАДАЧА 3. Руководство
некоторой компании решает, создавать ли для выпуска новой продукции крупное
производство, малое предприятие или продать патент другой фирме. Размер
выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного
состояния рынка (рисунок 5). Вероятность благоприятного и неблагоприятного
состояний экономической среды равна 0,5.
|
Номер стратегии |
Действия компании |
Выигрыш компании при состоянии экономической обстановки |
|
|
благоприятном (pБл= 0,5) |
неблагоприятном (pНбл = 0,5) |
||
|
A1 |
Строительство крупного предприятия |
200 000 у.е. |
- 180 000 у.е. |
|
A2 |
Строительство малого предприятия |
100 000 у.е. |
- 20 000 у.е. |
|
A3 |
Продажа патента |
10 000 у.е. |
10 000 у. е. |
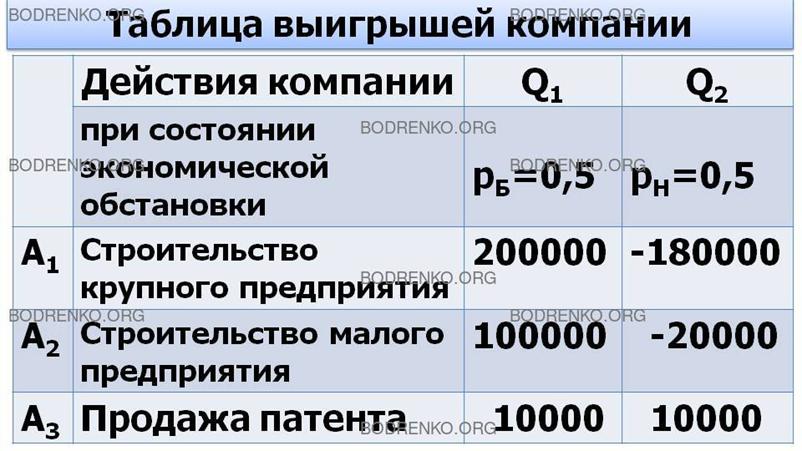
Рисунок 5. Таблица выигрышей компании.
На основе данной таблицы выигрышей (потерь) можно построить
дерево решений (рисунок 6).
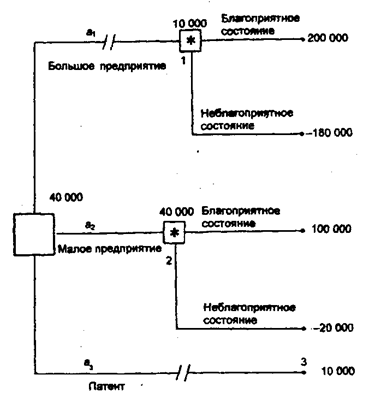
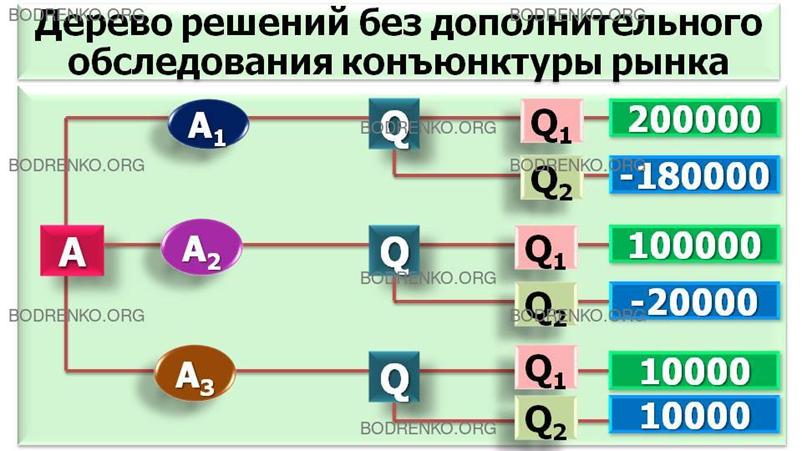
Рисунок
6. Дерево решений без дополнительного
обследования конъюнктуры рынка.
В рисунке 6 используются следующие обозначения: ÿ - решение (решение принимает ЛПР); [*]
- случай (решение "принимает" случай); // - отвергнутое решение.
Процедура принятия решения заключается в вычислении для
каждой (окончательной) вершины дерева (при движении справа налево) ожидаемых
денежных оценок (ОДО), отбрасывании неперспективных ветвей и выборе ветвей,
которым соответствует максимальное значение ОДО.
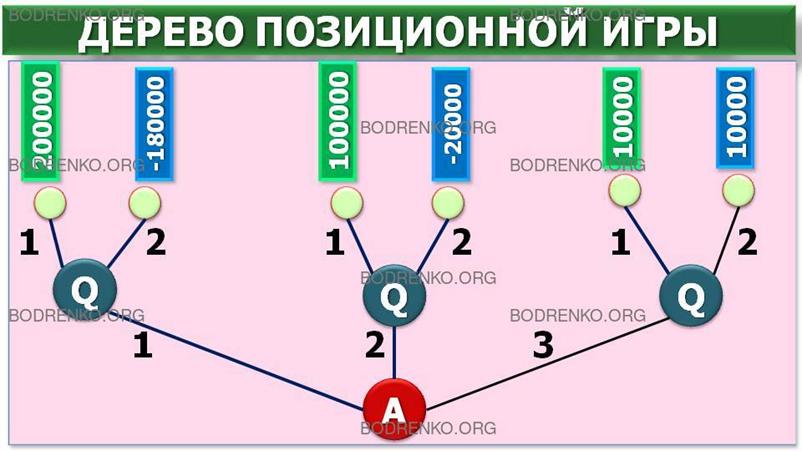
Заметим,
что данную задачу можно представить в виде позиционной игры, построив
соответствующее дерево игры.
Определим
средний ожидаемый выигрыш (ОДО):
1)
для альтернативы 1 (выбор стратегии A1) ОДО1
= 0,5*200 000 + 0,5(-180 000) = 10 000 у.е.;
2)
для альтернативы 2 (выбор стратегии A2) ОДО2
= 0,5*100 000 + 0,5(-20 000) = 40 000 у.е.;
3)
для альтернативы 3 (выбор стратегии A3) ОДО3
= 10 000 у.е.

ВЫВОД. НАИБОЛЕЕ ЦЕЛЕСООБРАЗНО ВЫБРАТЬ
СТРАТЕГИЮ A2,
Т.Е. СТРОИТЬ МАЛОЕ ПРЕДПРИЯТИЕ, А ВЕТВИ (СТРАТЕГИИ) A1 И A3 ДЕРЕВА РЕШЕНИЙ МОЖНО ОТБРОСИТЬ.
Ожидаемая денежная оценка (ОДО) наилучшего решения равна 40 000 у.е.
Следует отметить, что наличие состояния с вероятностями 50%
неудачи и 50% удачи на практике часто означает, что истинные вероятности игроку
(ЛПР), скорее всего, неизвестны и он всего лишь принимает такую гипотезу (так
называемое предположение «fifty - fifty» - пятьдесят на пятьдесят).
Усложним
рассмотренную выше задачу.
ЗАДАЧА 4. Пусть в условиях задачи 3 перед тем,
как принимать решение о строительстве, руководство компании должно определить,
заказывать ли дополнительное исследование состояния рынка или нет, причем предоставляемая
услуга обойдется компании в 10 000 у.е.
Руководство понимает, что дополнительное исследование
по-прежнему не способно дать точной информации, но оно поможет уточнить
ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей. Относительно
фирмы, которой можно заказать прогноз, известно, что она способна уточнить значения
вероятностей благоприятного или неблагоприятного исхода. Возможности фирмы в виде
условных вероятностей благоприятности и неблагоприятности рынка сбыта представлены
в таблице (рисунок 7).
|
Прогноз фирмы |
Фактически |
|
|
Благоприятный |
Неблагоприятный |
|
|
Благоприятный |
0,78 |
0,22 |
|
Неблагоприятный |
0,27 |
0,73 |
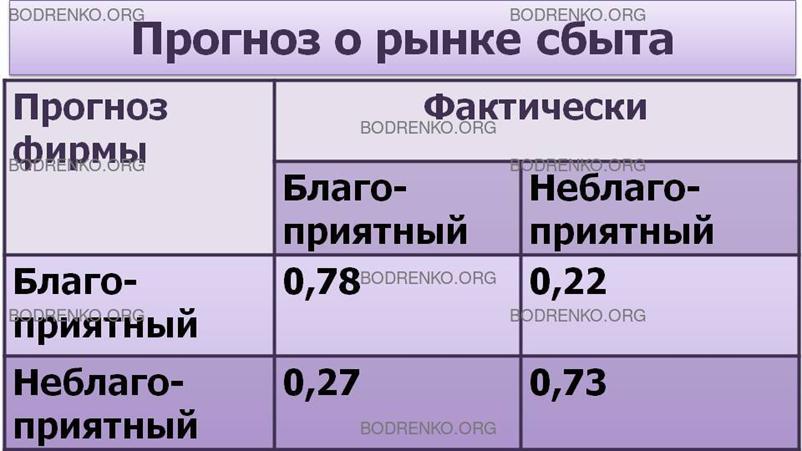
Рисунок 7. Прогноз фирмы о рынке сбыта.
Например, когда фирма утверждает, что рынок благоприятный,
то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут
возникнуть неблагоприятные условия), прогноз фирмы о неблагоприятности рынка
оправдывается с вероятностью 0,73.
Предположим,
что фирма, которой заказали прогноз состояния рынка, утверждает:
1)
ситуация будет благоприятной с
вероятностью 0,45;
2)
ситуация будет неблагоприятной с
вероятностью 0,55.
На основании дополнительных сведений можно построить новое
дерево решений (рисунок 8), где развитие событий происходит от корня дерева к
исходам, а расчет прибыли выполняется от конечных состояний к начальным.
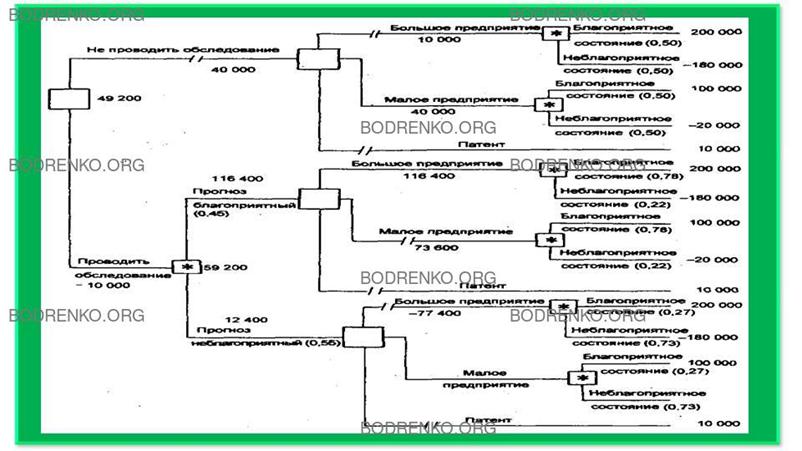
Рисунок
8. Дерево решений при дополнительном обследовании рынка.
В рисунке 8 используются следующие обозначения: ÿ - решение (решение принимает ЛПР); [*]
- случай (решение "принимает" случай); // - отвергнутое решение.
Определим средний ожидаемый выигрыш
(ОДО), если прогноз благоприятный:
1)
для альтернативы 1 (выбор стратегии A1) ОДО1
= 0,78*200000 + 0,22(-180000) = 116400 у.е.;
2)
для альтернативы 2 (выбор стратегии A2) ОДО2
= 0,78*100000 + 0,22(-20000) = 73600
у.е.;
3)
для альтернативы 3 (выбор стратегии A3) ОДО3
= 10000 у.е.

Определим средний ожидаемый выигрыш
(ОДО), если прогноз неблагоприятный:
1)
для альтернативы 1 (выбор стратегии A1)
ОДО1 = 0,27*200 000 + 0,73(-180 000) = – 77400 у.е.;
2)
для альтернативы 2 (выбор стратегии A2)
ОДО2 = 0,27*100 000 + 0,73(-20 000) = 12400 у.е.;
3)
для альтернативы 3 (выбор стратегии A3) ОДО3
= 10000 у.е.

Анализируя
дерево решений, можно сделать следующие выводы.
ВЫВОДЫ.
Необходимо проводить дополнительное исследование конъюнктуры
рынка, поскольку это позволяет существенно уточнить принимаемое решение; Если
фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно строить большое
предприятие (ожидаемая максимальная прибыль 116 400 у.е.), если прогноз не благоприятный
- малое (ожидаемая максимальная прибыль 12 400 у.е.).
КАК
РАССЧИТАТЬ ОЖИДАЕМУЮ ЦЕННОСТЬ ТОЧНОЙ ИНФОРМАЦИИ?
Предположим, что консультационная фирма за определенную плату
готова предоставить информацию о
фактической ситуации на рынке в тот момент, когда руководству компании надлежит
принять решение о масштабе производства. Принятие предложения зависит от соотношения
между ожидаемой ценностью (результативностью) точной информации и величиной
запрошенной платы за дополнительную (истинную) информацию, благодаря которой
может быть откорректировано принятие решения, т.е. первоначальное действие может
быть изменено.
ОЖИДАЕМАЯ ЦЕННОСТЬ ТОЧНОЙ ИНФОРМАЦИИ О ФАКТИЧЕСКОМ СОСТОЯНИИ
РЫНКА РАВНА РАЗНОСТИ МЕЖДУ ОЖИДАЕМОЙ ДЕНЕЖНОЙ ОЦЕНКОЙ (ОДО) ПРИ НАЛИЧИИ ТОЧНОЙ
ИНФОРМАЦИИ И МАКСИМАЛЬНОЙ ОЖИДАЕМОЙ ДЕНЕЖНОЙ ОЦЕНКОЙ ПРИ ОТСУТСТВИИ ТОЧНОЙ
ИНФОРМАЦИИ.
Рассчитаем ожидаемую ценность точной информации для примера,
в котором дополнительное обследование
конъюнктуры рынка не проводится. При отсутствии точной информации, как уже было
показано выше, максимальная ожидаемая денежная оценка равна:
ОДО
= 0,5 * 100 000 - 0,5 * 20 000 = 40
000 у.е.
Если точная информация об истинном состоянии рынка будет
- благоприятной: ОДО =200 000 у.е. (рисунок 8), принимается
решение строить крупное производство;
- если неблагоприятной, то наиболее целесообразное решение -
продажа патента (ОДО=10 000 у.е.).
Учитывая, что вероятности благоприятной и неблагоприятной
ситуаций равны 0,5, значение ОДОт.и (ОДО точной информации) определяется выражением:
ОДОт.и
= 0,5 * 200 000 + 0,5 * 10 000 = 105 000 у.е.
Тогда ожидаемая ценность точной информации (ОЦт.и)
равна:
ОЦт.и
= ОДОт.и - ОДО = 105 000 - 40 000 = 65 000 у.е.

Значение ОЦт.и показывает, какую максимальную
цену должна быть готова заплатить компания за точную информацию об истинном
состоянии рынка в тот момент, когда ей это необходимо.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Вентцель
Е.С. Элементы теории игр. М.: Физматгиз, 1961.
[2] Данилов
В.И. Лекции по теории игр. М.: Российская экономическая школа, 2001.

[3] Печерский
С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс. Учебное пособие.
СПб.: 2001.
[4] Фомин Г.П. Математические методы и модели в
коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы
и статистика, 2005. — 616 с: ил.
[5] Шикин Е. В. От игр к играм. Математическое
введение. Изд. 2-е, исправл. — М.: Едиториал УРСС, 2003. — 112 с.
