Теория игр. Антагонистические игры. Понятие матричной игры. Решение игры в чистых стратегиях. Ситуации равновесия. Седловые точки. Понятие смешанной стратегии. Аналитическое решение игры 2*2. Максиминная стратегия. Минимаксная стратегия. Теорема Неймана. Оптимальные смешанные стратегии. Платежная матрица
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость

1.
Понятие матричной игры.
2. Решение игры в чистых стратегиях.
Ситуации равновесия. Седловые точки.
3. Понятие смешанной стратегии.
Аналитическое решение игры 2*2.

РАЗДЕЛ 1. ПОНЯТИЕ МАТРИЧНОЙ ИГРЫ.
КАКИЕ ИГРЫ НАЗЫВАЮТСЯ АНТАГОНИСТИЧЕСКИМИ ИГРАМИ?
Игра — это идеализированная математическая модель
коллективного поведения: несколько индивидуумов (участников, игроков) влияют на
ситуацию (исход игры), причем их интересы
(их выигрыши при различных возможных ситуациях)
различны. Антагонизм интересов рождает конфликт, в то время как совпадение
интересов сводит игру к чистой координации, для осуществления которой
единственным разумным поведением является кооперация. Важным случаем в теории игр является
ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. налицо
прямой конфликт между игроками. Парные игры с нулевой суммой называются
антагонистическими играми.
Рассмотрим сначала простой пример
формализации конфликтной ситуации.
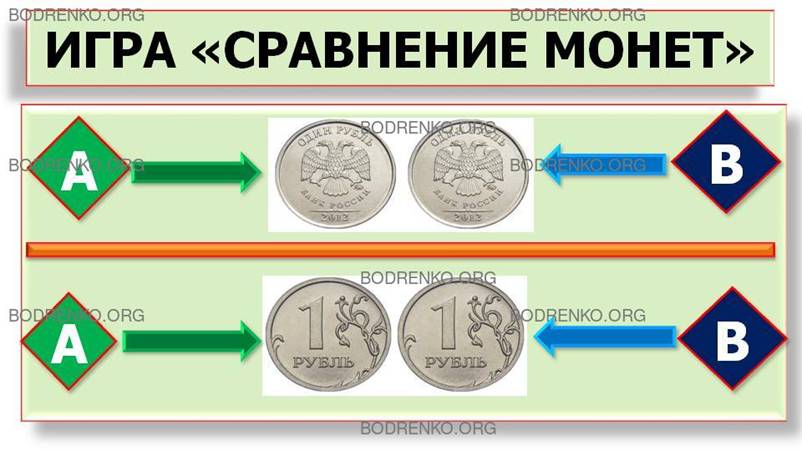
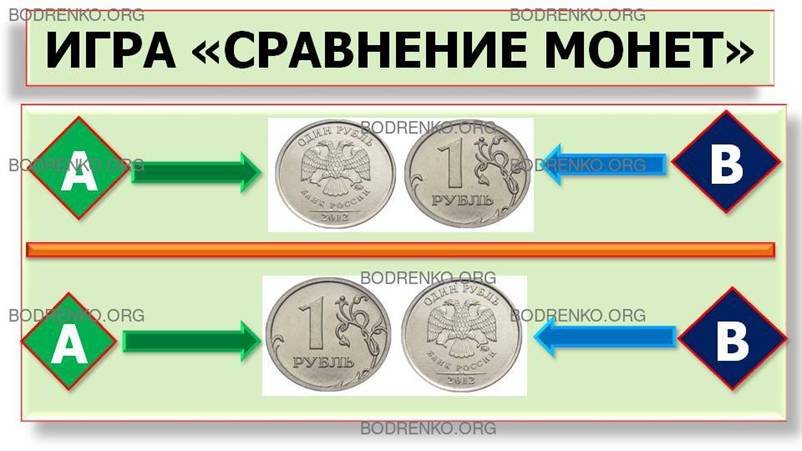
ПРИМЕР 1. ИГРА «СРАВНЕНИЕ МОНЕТ».
Каждый из двух
игроков одновременно и независимо друг от друга накрывает рукой монету вверх
гербом (эта сторона монеты по-другому называется «Орел») или вверх числом (эта
сторона монеты по-другому называется «Решка»).

Если оба игрока накрывают монеты вверх
«Орлом» или вверх «Решкой», то 1-й игрок выигрывает 1 рубль, а второй игрок
проигрывает 1 рубль. В ситуациях, когда оба игрока выбирают различные стороны
монет, то 1-й игрок проигрывает 1 рубль, а 2-й игрок соответственно этот 1
рубль выигрывает.
ЧТО
ОЗНАЧАЕТ ТЕРМИН «МАТРИЧНАЯ ИГРА»?
В
случае конечной игры двух лиц функции выигрыша каждого из игроков удобно
представлять в виде матрицы выигрышей, где строки представляют стратегии одного
игрока, столбцы — стратегии другого игрока, а в клетках матрицы указываются
выигрыши каждого из игроков в каждой из образующихся ситуаций. Данная форма
представления конечных игр двух лиц объясняет общее для них название –
матричные игры.
Например, в случае игры «сравнение монет» каждый из игроков имеет по две
стратегии, именуемые «Орел» и «Решка». Если игроки выбирают одинаковые стратегии, т.е. в случаях, если оба
накрывают монеты вверх «Орлом» или оба накрывают
монеты вверх «Решкой», то 1-й игрок выигрывает 1 рубль, а 2-й игрок проигрывает 1 рубль. В ситуациях, когда оба игрока выбирают различные стратегии, 1-й игрок проигрывает 1
рубль, а 2-й игрок соответственно этот 1
рубль выигрывает.

В итоге матрица выигрышей 1-го игрока
А, выглядит следующим образом:
|
Стратегии 1-го игрока |
Стратегии 2-го игрока |
|
|
«Орел» |
«Решка» |
|
|
«Орел» |
1 |
-1 |
|
«Решка» |
-1 |
1 |

Соответственно матрица выигрышей 2-го
игрока В имеет вид:
|
Стратегии 1-го игрока |
Стратегии 2-го игрока |
|
|
«Орел» |
«Решка» |
|
|
«Орел» |
-1 |
1 |
|
«Решка» |
1 |
-1 |

Для антагонистических игр, в которых
выигрыш одного игрока равен проигрышу другого (игр с нулевой суммой),
выполняется матричное
равенство В = – А. Игра «сравнение монет»,
очевидно, является примером
такой игры. Матричное соотношение В = – А показывает, что при анализе антагонистической игры
можно рассматривать выигрыши только одного из игроков. Пусть это будут,
например, выигрыши первого игрока A.
Начнем изучение теории игр с простейшей
статической модели — матричной игры, в которой участвуют два игрока, множество
стратегий каждого из игроков конечно, а выигрыш одного игрока равен проигрышу
другого.
Для
того чтобы составить экономико-математическую модель конфликтной ситуации в виде матричной игры, необходимо
построить матрицу выигрышей. Это весьма нетривиальная задача особенно для игр
большой размерности. В общем виде матрица игры (платежная матрица) строится
следующим образом:
1) перечисляем
все возможные чистые стратегии Ai
и Bj
игроков;
2) формализуем правила, по которым развивается
конфликт, в виде функции выигрышей
![]()
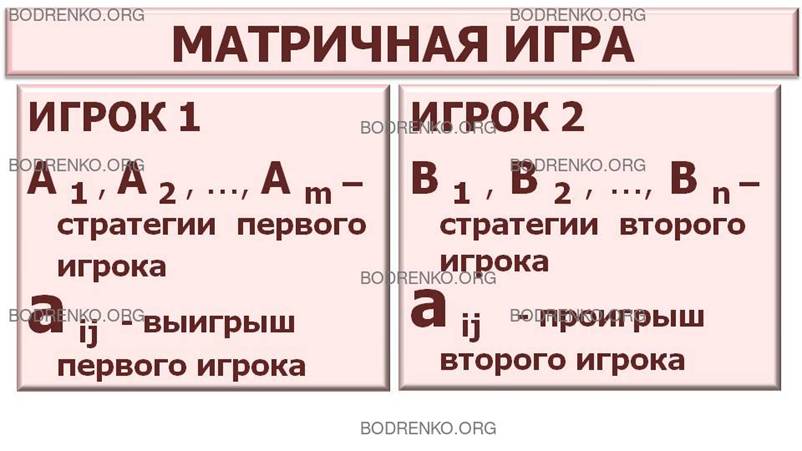
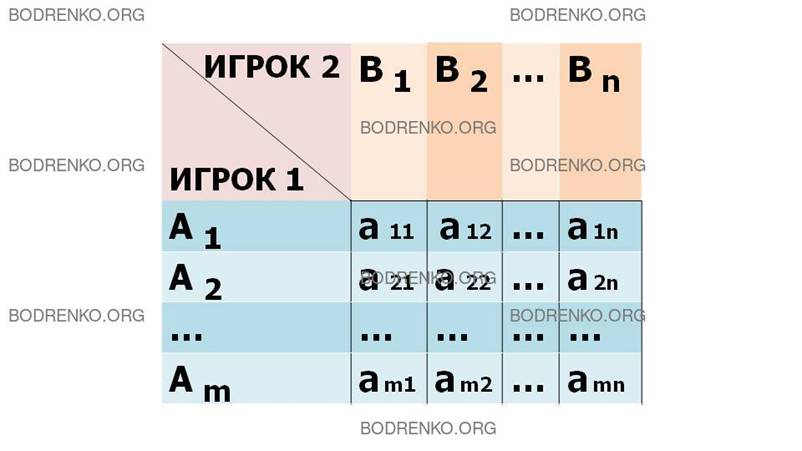
В общем
случае платежная матрица матричной игры
является прямоугольной (рис. 1).
|
Игрок 2 Игрок 1 |
B1 |
B2 |
… |
Bn |
|
A1 |
a11 |
a12 |
… |
a1n |
|
A2 |
a21 |
a22 |
… |
a2n |
|
… |
… |
… |
… |
… |
|
Am |
am1 |
am2 |
… |
amn |
Рис. 1. Платежная матрица.
Номер строки матрицы соответствует
номеру стратегии, применяемой игроком 1. Номер столбца соответствует номеру стратегии
игрока 2. Выигрыш игрока 1 является элементом матрицы. Выигрыш игрока 2 равен
проигрышу игрока 1. Матричные игры всегда имеют решения в смешанных стратегиях.
Они могут быть решены методами линейного программирования.
ПРИМЕР 2. ИГРА «ПОСТАВКА ТОВАРОВ».
На каждой из двух баз ассортиментный
минимум составляет один и тот же набор
из n видов товаров. Каждая база должна поставить в
свой магазин только одни из этих n видов товаров.
Магазины, назовем их «магазин A» и «магазин B»,
конкурируют между собой. Один и тот же вид товара продается в обоих магазинах
по одной и той же цене. Однако товар, поставляемый в «магазин B», более
высокого качества. Если
«магазин A»
завезет с базы товар i-го
вида, а «магазин B»
завезет с базы товар j-го вида, отличный от товара i-го вида (то есть i ≠ j), то товар i-го вида в
«магазине A»
будет пользоваться спросом, и «магазин A» получит
прибыль Ci
у.е.
Если же в «магазин A» и «магазин B» завезены
товары одинакового вида (то есть i = j),
то товар i-го
вида в «магазине A»
не будет пользоваться спросом, так как
такой же товар, но более высокого качества, продается в «магазине B» по такой же
цене. В этом случае (i=j) «магазин A» получит убытки Dj у.е. по транспортировке, хранению и,
возможно, порче товара i-го
вида в этом магазине. Требуется
составить платежную матрицу игры.
Решение. Формализуем
данную конфликтную ситуацию. Назовем ее игрой «Поставка товаров». Пусть в
качестве Игрока 1 выступает «магазин A», а в качестве Игрока 2 выступает «магазин B». Игрок 1 с целью достижения прибыли
имеет возможность выбрать одну из n стратегий Ai –
завезти со своей базы товар i-го вида. Игрок 2 также имеет возможность
выбрать одну из n стратегий Bj
– завезти со своей базы товар j-го
вида. Пусть игроки выбрали
стратегии {Ai,
Bj}.
Тогда можно определить следующую
функцию выигрышей Игрока 1.
![]()
Для каждого фиксированного номера i (i = 1, …, n)
имеем:
f(1,j) = C1
при 1 ≠ j,
f
(1,1) = - D1,
j
= 1, … n;
f(2,j) = C2
при 2 ≠ j,
f
(2,2) = - D2,
j
= 1, … n;
…
f(n,j) = Cn
при n
≠ j,
f
(n,n) = - Dn, j = 1, … n
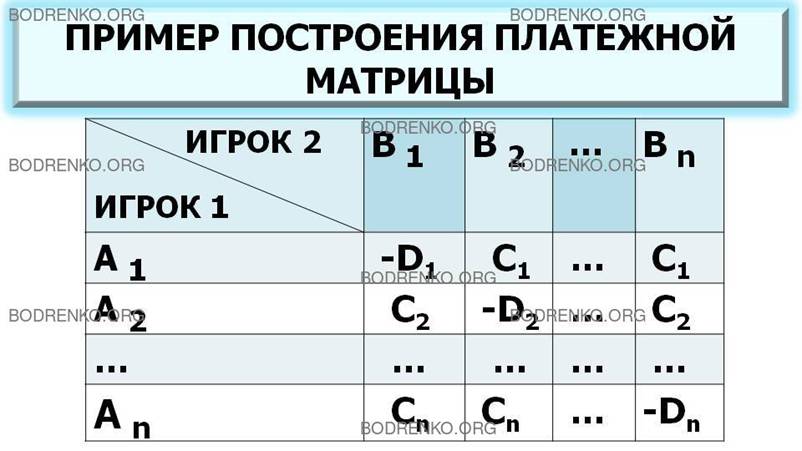
Платежная матрица (квадратная матрица
порядка n)
будет иметь следующий вид (рис. 2).
|
Игрок 2 Игрок 1 |
B1 |
B2 |
… |
Bn |
|
A1 |
-D1 |
C1 |
… |
C1 |
|
A2 |
C2 |
-D2 |
… |
C2 |
|
… |
… |
… |
… |
… |
|
An |
Cn |
Cn |
… |
-Dn |
Рис.
2. Платежная матрица игры «Поставка товаров».
МАТРИЧНАЯ ИГРА «m
x n».
Пусть игрок 1 имеет m стратегий A1,
A2,
…, Am , а игрок 2 имеет n стратегий B1, B2,
…, Bn
.
Игра может быть названа «игрой m
x n».
Представим матрицу игры двух лиц с нулевой суммой, сопроводив ее необходимыми обозначениями
(рис. 3).
|
Игрок 2 Игрок
1 |
B1 |
B2 |
… |
Bn |
αi |
|
A1 |
a11 |
a12 |
… |
a1n |
α1 |
|
A2 |
a21 |
a22 |
… |
a2n |
α2 |
|
… |
… |
… |
… |
… |
… |
|
Am |
am1 |
am2 |
… |
amn |
αm |
|
βj |
β1 |
β2 |
… |
βn |
|
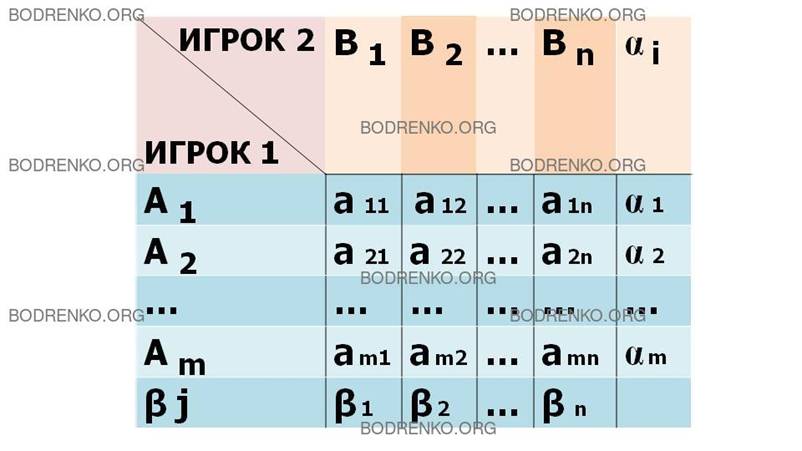
Рис.
3. Платежная матрица игры «m
x n».
В данной матрице элементы aij — это значения выигрышей игрока 1, они
могут означать и математическое ожидание
выигрыша (среднее значение), если выигрыш является случайной величиной.
Величины α1,
α2, …, αm
– это минимальные значения элементов a ij по строчкам.
Величины β1,
β2, …, βn –
это максимальные значения элементов a
ij по столбцам.
![]()
![]()
Их содержательный смысл будет отражен
ниже.
РАЗДЕЛ 2. РЕШЕНИЕ ИГРЫ В ЧИСТЫХ СТРАТЕГИЯХ. СИТУАЦИИ
РАВНОВЕСИЯ. СЕДЛОВЫЕ ТОЧКИ.
Рассмотрим матричную игру,
представленную матрицей выигрышей m x n,
где число строк равно числу m, а число столбцов равно числу n (рис. 3). Применим принцип получения максимального
гарантированного результата при наихудших условиях. Игрок 1 стремится принять такую стратегию,
которая должна обеспечить максимальный проигрыш игрока 2. Соответственно игрок 2 стремится принять
стратегию, обеспечивающую минимальный выигрыш игрока 1.

Рассмотрим оба этих подхода.
Подход игрока 1.
Он должен получить максимальный гарантированный результат при наихудших
условиях.
Значит, при выборе отвечающей этим
условиям своей чистой i-й стратегии (на рис. 3 этой стратегии соответствует i-я
строка выигрышей) он должен выбрать гарантированный результат в наихудших
условиях, т.е. наименьшее значение своего выигрыша a ij , которое обозначим αi
.
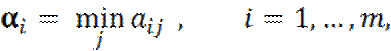
Чтобы этот гарантированный эффект в
наихудших условиях был максимальным, нужно из всех αi выбрать наибольшее значение.
Обозначим его α и назовем чистой
нижней ценой игры («максимин»):
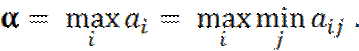
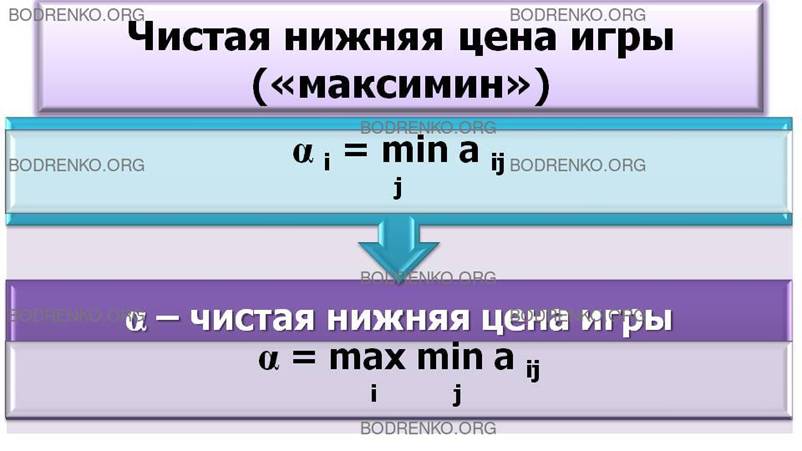
Таким образом, максиминной стратегии
отвечает строка матрицы, которой соответствует элемент α. Какие
бы стратегии ни применял игрок 2, игрок 1 максиминной чистой стратегией
гарантировал себе выигрыш не меньший, чем α.
Таково оптимальное поведение игрока 1.
Подход игрока 2.
Своими оптимальными стратегиями он стремится уменьшить выигрыш игрока 1,
поэтому при каждой j-й чистой стратегии он отыскивает величину своего
максимального проигрыша βj в каждом j-м столбце
![]()
То есть игрок 2 определяет максимальный выигрыш игрока 1,
если игрок 2 применит j-ю чистую стратегию.
Из всех своих n чистых стратегий B1, B2,
…, Bn игрок 2 отыскивает такую, при которой игрок 1
получит минимальный выигрыш, то есть
игрок 2 определяет ![]() - чистую верхнюю цену игры («минимакс»):
- чистую верхнюю цену игры («минимакс»):
![]()
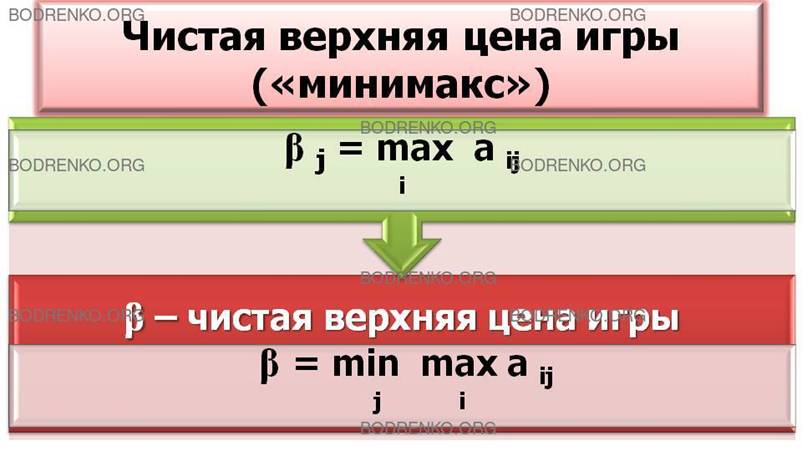
Чистая верхняя цена игры показывает,
какой максимальный выигрыш может гарантировать игрок 1, применяя свои чистые
стратегии, – выигрыш, не меньший, чем α.
Игрок 2 за счет указанного выше выбора
своих чистых стратегий не допустит, чтобы иuрок 1 мог получить выигрыш, больший,
чем β.
Таким образом, минимаксная стратегия отображается столбцом платежной матрицы, в
котором находится элемент β (рис. 3).
Она является оптимальной чистой
гарантирующей стратегией игрока 2, если он ничего не знает о действиях игрока
1.
Чистая цена игры ν
есть цена данной игры, если
нижняя и верхняя ее цены совпадают, то есть
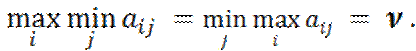
В этом случае игра называется игрой с седловой точкой.
ЧТО ТАКОЕ
«СЕДЛОВАЯ ТОЧКА»?
Элемент aij, матрицы выигрышей А,
соответствующий максиминной и минимаксной стратегиям, называется седловой точкой матрицы
A (это объясняется формой графика
функции выигрыша в точке aij: она напоминает седло, убывая при изменении одной из переменных и возрастая при
изменении другой переменной.
КАКАЯ АНТАГОНИСТИЧЕСКАЯ ИГРА НАЗЫВАЕТСЯ
СПРАВЕДЛИВОЙ?
В случае, если цена антагонистической
игры равна нулю: v = 0, то игра называется справедливой.
В итоге будет разумно ожидать, что в
описанной выше игре с седловой точкой противники будут придерживаться избранных
стратегий.
Матричная игра, для которой max min aij
= min max aij, называется вполне определенной, или игрой, имеющей
решение в чистых стратегиях.
Однако далеко не все матричные игры являются
вполне определенными, и в общем случае игры, в которых выполняется строгое
неравенство: max min aij < min
max aij, называются не полностью определенными играми (или
не имеющими решения в чистых стратегиях играми.
ПРИМЕР 3.
Определить верхнюю и нижнюю цены при
заданной матрице игры и указать максиминную и минимаксную стратегии.
Задана матрица игры (рис. 4).
|
Игрок 2 Игрок
1 |
B1 |
B2 |
B3 |
αi |
|
A1 |
2 |
1 |
3 |
1 |
|
A2 |
4 |
5 |
6 |
4 |
|
βj |
4 |
5 |
6 |
|
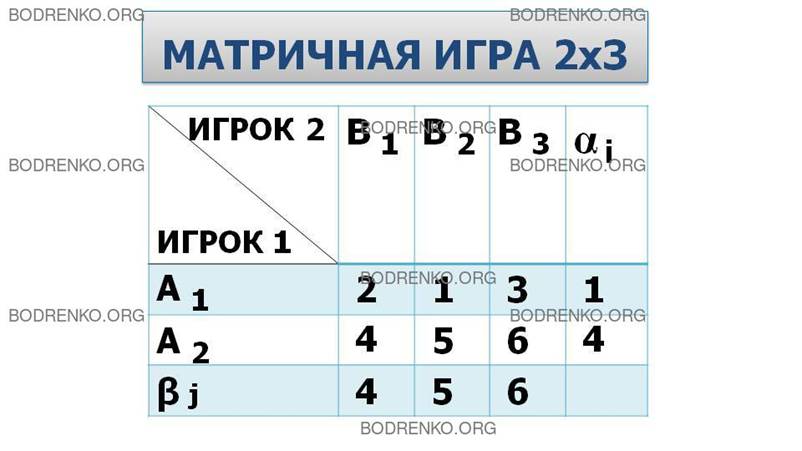
Рис.
4. Матричная игра 2 x
3 с седловой точкой.
Решение. Определим нижнюю цену игры
α:
α 1 = 1; α 2
= 4; α = 4 (см. столбец αi).
Определим верхнюю цену игры β:
β 1 = 4; β 2
= 5; β 3 = 6; β = 4 (см. строку βj).
Таким образом, α = β = 4,
т.е.
![]()
Значит, α = β = ν
= 4 – чистая цена игры при стратегиях А2 и В 1 . Следовательно, имеем игру с седловой точкой. Максиминная
стратегия игрока 1 – A2,
минимаксная стратегия игрока 2 – B1.

ПРИМЕР 4.
Определим максиминную и минимаксную
стратегии игроков при заданной платежной матрице (рис. 5).
|
Игрок 2 Игрок
1 |
B1 |
B2 |
B3 |
B4 |
αi |
|
A1 |
2 |
7 |
9 |
10 |
2 |
|
A2 |
8 |
5 |
4 |
6 |
4 |
|
βj |
8 |
7 |
9 |
10 |
|
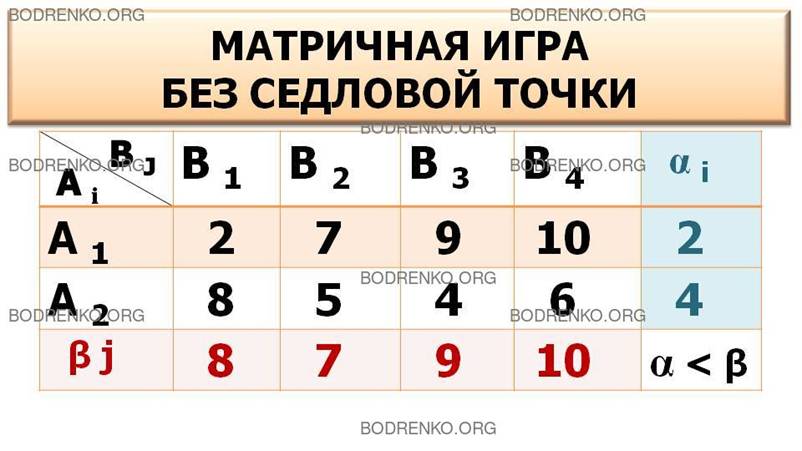
Рис. 5. Матричная игра «2 x 4»
без седловой точки.
Решение. Определим максиминную
стратегию:
α 1 = 2; α 2
= 4; α = 4 (см. столбец αi).
Максиминная стратегия игрока 1 – А2 .
Определим минимаксную стратегию:
β 1 = 8; β 2
= 7; β 3 = 9; β 4 = 10; β = 7 (см.
строку βj).
Минимаксная стратегия игрока 2 –
В2 . Здесь α< β, следовательно, седловой точки
нет.

Рассмотрим следующий пример
подобной игры.
ПРИМЕР 5.
Предприниматель располагает тремя
видами товаров: А1, А2, А3, которые он стремится реализовать на рынке, где
возможна продажа конкурентом аналогичных товаров: В1, В2, В3, соответственно. Предпринимателю не
известно, какой вид товаров
преимущественно конкурент будет продавать на рынке, а конкуренту не
известно, какие товары предпринимателя на этом рынке появятся. Предприниматель
располагает данными о том, какова
вероятность продать тот или иной товар при наличии на рынке товаров
конкурента. Эти данные образуют матрицу игры (таблица 1). Необходимо дать предпринимателю
рекомендации по рациональному выбору
вида товаров для продвижения их на рынок в условиях конкуренции, при котором
обеспечивается получение наилучшего возможного результата - наибольшей
вероятности продаж, что бы ни предпринимал конкурент.
Таблица 1.
|
Предприниматель |
Конкурент |
|||
|
B1 |
B2 |
B3 |
ai |
|
|
A1 |
0,5 |
0,4 |
0,9 |
0,4 (*) |
|
A2 |
0,2 |
0,9 |
0,1 |
0,1 |
|
A3 |
0,8 |
0,0 |
1,0 |
0,0 |
|
bj |
0,8 (*) |
0,9 |
1,0 |
|
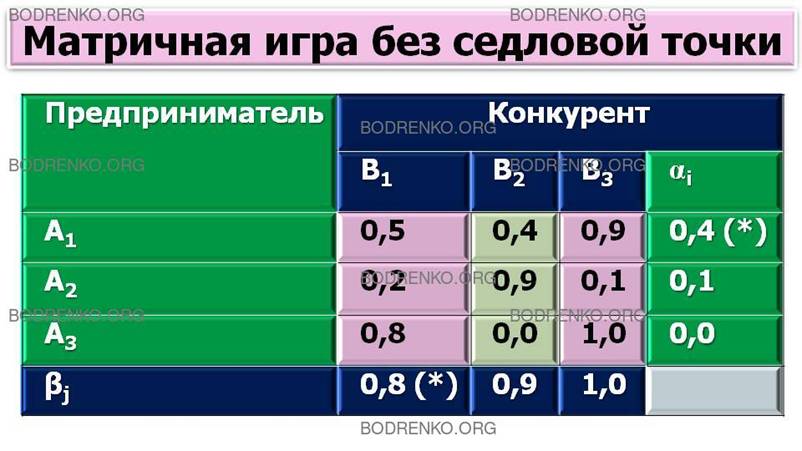
Решение.
Выписываем в крайнем правом столбце минимумы
значений по строкам и из них выбираем наибольший a1 = 0,4 (отмечен звездочкой). Это нижняя
цена игры, или максимин. Затем выписываем в нижней строке максимумы значений по столбцам и
из них выбираем наименьший b1 = 0,8 (отмечен звездочкой). Это верхняя цена
игры, или минимакс. Решение заключается в том, что необходимо систематически применять максиминную
стратегию - товар типа А1. При этом предпринимателю гарантируется результат не менее p
= 0,4, что бы ни предпринимал конкурент (его замыслы нам не известны). Для
конкурента наилучшая стратегия - выбор товара вида В1; при этом он гарантирует себе
результат не более p = 0,8 (чем прибыль предпринимателя больше, тем для него
хуже). Поскольку в рассмотренном примере нет седловой точки (α < β), это означает, что полученные
рекомендации верны лишь для случая, когда конкурент не располагает данными об
избранном предпринимателем решении. Это так называемая неустойчивая стратегия.
Если конкурент узнает о том, что предприниматель стал применять товар типа А2,
он сразу же начнет применять товар вида В3 и тем самым улучшит свой результат
до p = 0,1. В тех случаях, когда в подобной
задаче конкурент располагает данными о
выборе предпринимателя, необходимо искать
решение в смешанных стратегиях.
ВЫБОР ОПТИМАЛЬНЫХ СТРАТЕГИЙ.
1.
В игре с седловой точкой.
Если матрица игры содержит элемент,
минимальный в своей строке и максимальный в своем столбце, то он, как уже
сказано выше, является седловой точкой. В этом случае мы имеем игру с седловой
точкой.
Если
в игре с седловой точкой один игрок придерживается седловой точки, тогда другой
получит лучший результат, если также будет придерживаться этой точки. Лучшее
поведение игрока не должно повлечь уменьшение его выигрыша. Зато худшее
поведение может привести к этому. В данном случае решением игры являются:
•
чистая стратегия игрока 1;
•
чистая стратегия игрока 2;
•
седловой элемент.
В данном случае оптимальные чистые
стратегии – это чистые стратегии, образующие седловую точку.
2.
В игре без седловой точки.
Если игрок 1 информирован о стратегии,
принятой игроком 2, он сможет принять оптимальную стратегию, которая не
совпадает с максиминной.
Рассмотрим следующий пример.
ПРИМЕР 6.
Дана матрица игры (рис. 6):
|
Игрок 2 Игрок
1 |
B1 |
B2 |
B3 |
B4 |
B5 |
αi |
|
A1 |
7 |
5 |
3 |
6 |
11 |
3 |
|
A2 |
8 |
4 |
6 |
7 |
9 |
4 |
|
βj |
8 |
5 |
6 |
7 |
11 |
|

Рис. 6. Матричная игра «2 x 5»
без седловой точки.
Определим минимаксную стратегию игрока
2:
β 1 = 8; β 2
= 5; β 3 = 6; β 4 = 7; β 5 = 11; β = 5 (см.
строку βj).
Верхняя цена игры β = 5;
минимаксная стратегия игрока 2 – В2 .
Допустим, что игроку 1 стало известно,
что игрок 2 принял минимаксную стратегию. Игрок 1 должен выбрать оптимальную стратегию
при условии, что В2 – стратегия игрока 2 (β =5).
Решение.
Определим максиминную стратегию игрока
1:
α 1 = 3; α 2
= 4; α = 4 (см. столбец αi).
Максиминная стратегия игрока 1 – А2 .
Здесь α< β (4<5),
следовательно, седловой точки нет.
Выберем оптимальную стратегию для
игрока 1 при условии, что игрок 1 знает, что игрок 2 принял минимаксную
стратегию B2.
Ею будет не максиминная А2,
дающая игроку 1 выигрыш α = 4, а та стратегия, которая соответствует
максимальному элементу в столбце В2.
То есть max
a i2 = 5 – это элемент a 12, который находится в первой строке
матрицы - в строке A1.
В этом случае максимальный
гарантированный выигрыш игрока 1 будет равен верхней цене игры β = 5,
поэтому игрок 1 выбирает свою оптимальную стратегию А1 , зная, что
игрок 2 выбрал свою стратегию В2 .
Таким образом, рассмотренный пример
дает результат, отличный от результата при игре с седловой точкой. На примере 6
показано, что бывают ситуации, когда игрок 1 может получить выигрыш,
превосходящий максиминный, если ему известны намерения игрока 2.
Стратегия является оптимальной, если ее
применение обеспечит игроку наибольший гарантированный выигрыш при любых
возможных стратегиях другого игрока. При многократном повторении игры в сходных
условиях можно добиться гарантированного среднего выигрыша, превосходящего для
игрока 1 максиминный.
РАЗДЕЛ 3. ПОНЯТИЕ СМЕШАННОЙ СТРАТЕГИИ. АНАЛИТИЧЕСКОЕ
РЕШЕНИЕ ИГРЫ 2*2.
ПОНЯТИЕ СМЕШАННОЙ СТРАТЕГИИ.
Рассмотрим теперь подробнее случай,
когда в игре отсутствует седловая точка, то есть случай, когда α < β. Если в матричной игре отсутствует седловая
точка в чистых стратегиях, то находят верхнюю и нижнюю цены игры. Они
показывают, что игроку 1 гарантирован выигрыш, не меньший нижней цены игры
α. А игрок 2 может обеспечить себе проигрыш, не больший β, то
есть игрок 1 не получит выигрыша,
превосходящего верхнюю цену игры β.
В примере 6 игрок 1 получил при своей
оптимальной стратегии А1, отличной от максиминной, выигрыш, равный верхней цене игры β = 5.
Такова плата за информированность о стратегии игрока 2. Это крайний случай. Не улучшится ли результат игрока 1, если
информация о действиях противной стороны будет отсутствовать, но игрок будет
многократно применять чистые стратегии случайным образом с определенной
вероятностью? Возникает вопрос, как «справедливо» разделить разность (β – α > 0)
между игроками? Оказывается, что компромиссного распределения разности (β
– α) между игроками можно добиться путем случайного чередования игроками
чистых стратегий. При этом игрок 1 может получать выигрыши, в среднем большие
нижней цены игры α, но меньшие верхней цены игры β. Для этого применяют смешанные стратегии,
которые можно представить в виде случайных величин, возможными значениями
которых являются чистые стратегии.
Пусть для
игрока 1 смешанная стратегия S1
заключается в применении
чистых стратегий А1, А2,..., Аm с соответствующими вероятностями р1,
р2, ..., pm:
![]()
где
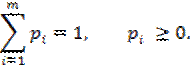

Число ![]() – это
вероятность того, что игрок 1 применит чистую стратегию
– это
вероятность того, что игрок 1 применит чистую стратегию ![]()
Для игрока 2 смешанная стратегия S2
заключается в применении чистых стратегий B1, B2,
… Bn с вероятностями q1, q2,
…, qn:
![]()
где


Число ![]() –
это вероятность того, что игрок 2 применит чистую стратегию
–
это вероятность того, что игрок 2 применит чистую стратегию ![]() .
.
В случае,
когда pi = 1 , для
игрока 1 имеем чистую стратегию Ai:
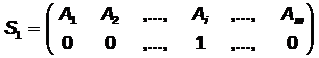
Если мы
окажемся в ситуации {Ai,
Bj},
то есть когда игрок 1 применит стратегию Ai, а игрок 2 при этом применит стратегию
Bj,
то она реализуется с вероятностью
![]() .
.
В матричной
игре, зная платежную матрицу A
(она относится и к игроку 1, и к игроку 2), можно определить средний выигрыш
игрока 1:
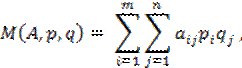
где p, q
– векторы с компонентами pi,
qj,
соответственно.
Стратегии ![]() и
и ![]()
называются
оптимальными смешанными стратегиями игроков, если выполнено следующее условие
оптимальности:
![]() (*)
(*)

Поясним
полученные соотношения.
Левая часть
этого неравенства
![]()
означает, что
если первый игрок отклоняется от оптимальной стратегии p0, то его
выигрыш может только уменьшиться при условии, что второй игрок придерживается
оптимальной стратегии q0.
Аналогично,
неравенство
![]()
означает, что
если второй игрок отклоняется от оптимальной стратегии q0, то его
проигрыш может только увеличиться.
Условие оптимальности (*) аналогично условию:
![]()
Величина
![]()
называется
ценой игры.
Решить игру
означает найти цену игры и оптимальные стратегии. То есть решением игры
является нахождение «набора» (![]() . Естественно,
что возникают следующие вопросы.
. Естественно,
что возникают следующие вопросы.
КАКИЕ МАТРИЧНЫЕ ИГРЫ ИМЕЮТ РЕШЕНИЕ В
СМЕШАННЫХ СТРАТЕГИЯХ И КАК НАЙТИ ЭТО РЕШЕНИЕ, ЕСЛИ ОНО СУЩЕСТВУЕТ?
Ответ на этот
вопрос дает основная теорема теории матричных игр.
ТЕОРЕМА (НЕЙМАНА).
Для матричной
игры с любой матрицей A
величины
![]()
![]()
существуют и
равны между собой:
![]()
Более того,
существует, по крайней мере, одна ситуация
![]() ), для которой выполняется соотношение:
), для которой выполняется соотношение:
![]()


Другими
словами, любая матричная игра имеет решение в смешанных стратегиях.
В состав оптимальных смешанных стратегий игроков могут входить не все чистые
стратегии Ai, B j. То есть вероятности некоторых из них
будут равны нулю: ![]() ,
, ![]()
Значит, не
все заданные чистые стратегии игроков будут входить априори в их оптимальные
смешанные стратегии. Тогда те чистые
стратегии, которые входят в оптимальные смешанные стратегии, называются активными чистыми стратегиями.
Справедлива
следующая теорема.
ТЕОРЕМА.
Оптимальная смешанная стратегия p0 первого
игрока смешивается только из тех чистых стратегий Ai,
![]() , для которых справедливы равенства:
, для которых справедливы равенства:
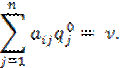
А в
оптимальной смешанной стратегии q0 второго
игрока смешиваются только те стратегии Bj,
![]() , для которых
справедливы равенства:
, для которых
справедливы равенства:
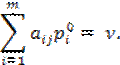


Перечислим
условия применения смешанных стратегий:
1. Игра
без седловой точки;
2. Игроки
используют случайную смесь чистых стратегий с заданными вероятностями;
3. Игра
многократно повторяется в сходных условиях;
4. При
любом ходе ни один из игроков не информирован о
стратегии другого игрока;
5. Допускается
усреднение результатов игр.

ОПТИМАЛЬНЫЕ СМЕШАННЫЕ СТРАТЕГИИ В
МАТРИЧНОЙ ИГРЕ «2x2».
Рассмотрение
методов нахождения оптимальных смешанных стратегий для матричных игр начнем с
простейшей игры, описываемой матрицей «2х2». При отсутствии седловой точки можно получить
две оптимальные смешанные стратегии. Как уже отмечалось, эти смешанные
стратегии записываются так:
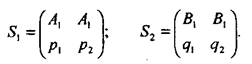
Значит, имеется платежная матрица
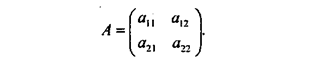
При этом
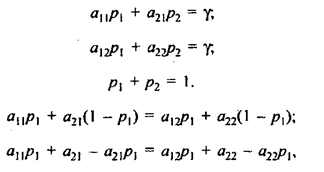
откуда получаем оптимальные значения ![]() и
и ![]() :
:
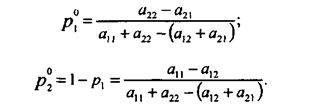

Зная ![]() и
и ![]() находим ν:
находим ν:
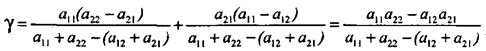
Вычислив ν, находим ![]() и
и ![]() :
:
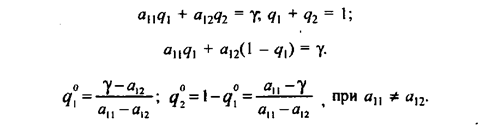

Задача решена, так как найдены векторы
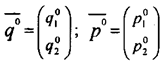
и цена игры ν.
ДОМИНИРОВАНИЕ СТРАТЕГИЙ.
Вообще говоря, оптимальные стратегии
легко находятся для небольших
игр, но вычисления становятся достаточно сложными с ростом числа стратегий. Для поиска
оптимальных стратегий рекомендуется
несколько подходов. Для уменьшения размерности игры используется доминирование строк
и столбцов. Доминирование представляет
отношение между стратегиями, наличие которого во многих практических случаях
дает возможность сократить размеры исходной платежной матрицы игры.
Обычно говорят, что k-я
строка матрицы A доминирует i-ю
строку (т.е. одна чистая стратегия доминирует другую), если aij < = akj для всех j, и при этом aij < akj хотя бы для одного j. То есть k-я строка является доминирующей строкой.
Аналогично, s-й столбец доминирует j-й столбец, если ais < = aij для всех i, и при этом ais < aij хотя бы для одного i. То есть s-й столбец является доминирующим столбцом в платежной матрице.
Смысл этих определений состоит в том, что доминирующая стратегия никогда не хуже, а в некоторых случаях даже лучше,
чем доминируемая стратегия. Отсюда следует, что игроку нет необходимости использовать доминируемую стратегию. В самом
деле, будут существовать оптимальные смешанные стратегии, при которых вероятность использования доминируемых строк и столбцов
равна нулю, и при решении игры все доминируемые строки и столбцы могут быть отброшены, что позволяет
уменьшить размеры матрицы. Этот
подход может использоваться также при поиске решения игры в чистых стратегиях.
Рассмотрим
это понятие на примере матрицы
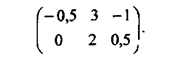
Рассуждая с
позиции игрока 2, можно обнаружить преимущество его третьей стратегии перед
второй, поскольку при первой стратегии игрока 1 выигрыш игрока 2 равен —3
(вторая стратегия) и 1 (третья стратегия), а при второй стратегии игрока 1
выигрыш игрока 2 равен —2 (вторая стратегия) и - 0,5 (третья стратегия).
Таким
образом, при любой стратегии игрока 1 игроку 2 выгоднее применять свою третью
стратегию по сравнению со второй; при наличии третьей стратегии игрок 2, если
он стремится играть оптимально, никогда не будет использовать свою вторую
стратегию, поэтому ее можно исключить из игры, т.е. в исходной платежной
матрице можно вычеркнуть 2-й столбец:
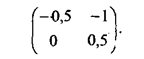
С позиции
игрока 1 его первая стратегия оказывается хуже второй, так как по первой
стратегии он только проигрывает. Поэтому первую стратегию можно исключить, а
матрицу игры преобразовать к виду:
(0 0,5).
Учитывая
интересы игрока 2, следует оставить только его первую стратегию, поскольку,
выбирая вторую стратегию, игрок 2 оказывается в проигрыше (0,5 - выигрыш игрока
1), и матрица игры принимает простейший вид: (0), т.е. имеется седловая точка.
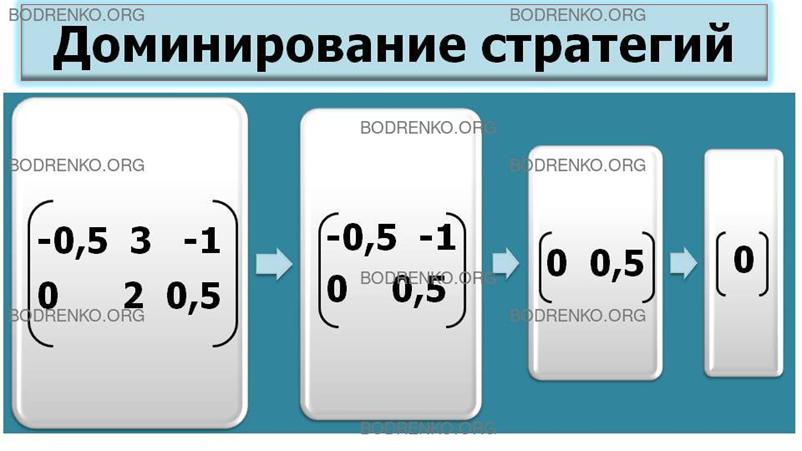
Доминирование
можно распространить и на смешанные стратегии. Если элементы одной строки не
все меньше (или равны) соответствующих элементов других строк, но все меньше
(или равны) некоторых выпуклых линейных комбинаций соответствующих элементов
других строк, то эту стратегию можно исключить, заменив ее смешанной
стратегией с соответствующими частотами использования чистых стратегий. В
качестве иллюстрации к сказанному рассмотрим матрицу игры:
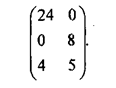
Для первых двух чистых стратегий игрока
1 возьмем частоты их применения (вероятности) равными 0,25 и 0,75. Третья
стратегия игрока 1 доминируется линейной выпуклой комбинацией первой и второй
чистых стратегий, взятых с частотами 0,25 и 0,75 соответственно, т.е.
смешанной стратегией:
24*0,25
+ 0*0,75 = 6 > 4;
0*0,25
+ 8*0,75 = 6 > 5.
Поэтому
третью стратегию игрока 1 можно исключить, используя вместо нее указанную выше
смешанную стратегию.

Аналогично, если
каждый элемент некоторого столбца больше или равен некоторой выпуклой линейной
комбинации соответствующих элементов некоторых других столбцов, то этот
столбец можно исключить из рассмотрения (вычеркнуть из матрицы). Например, для
матрицы
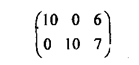
третья
стратегия игрока 2 доминируется смешанной стратегией из первой и второй его
чистых стратегий, взятых с частотами 0,5 и 0,5:
10*0,5
+ 0*0,5 = 5 < 6;
0*0,5
+ 10*0,5 = 5 < 7.
Таким
образом, исходная матрица игры эквивалентна матрице следующего вида:
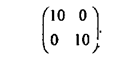
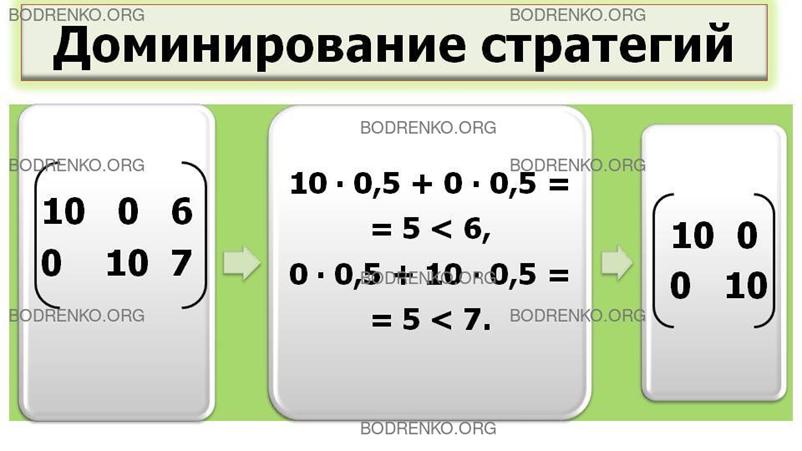
Как видно,
возможности доминирования смешанными стратегиями в отличие от чистых
значительно менее прозрачны (нужно должным образом подобрать частоты
применения чистых стратегий), но такие возможности есть, и ими полезно уметь
пользоваться.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Вентцель Е.С. Элементы теории игр. М.: Физматгиз, 1961.
[2] Данилов В.И. Лекции по теории игр. М.: Российская
экономическая школа, 2001.

[3] Печерский С.Л., Беляева А.А. Теория игр для экономистов.
Вводный курс. Учебное пособие. СПб.: 2001.
[4] Фомин Г.П.
Математические методы и модели в коммерческой деятельности: Учебник. — 2-е
изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.
[5] Шикин Е.
В. От игр к играм. Математическое введение. Изд. 2-е, исправл. — М.: Едиториал
УРСС, 2003. — 112 с.
