Теория риска и моделирование рисковых ситуаций.

 

Лекция 4.  Игры с природой в условиях стохастической неопределенности.

1. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ РИСКА (СТОХАСТИЧЕСКОЙ НЕОПРЕДЕЛЕННОСТИ).

2. КРИТЕРИИ ПРИНЯТИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ В УСЛОВИЯХ РИСКА.

3. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА В ИГРАХ С ПРИРОДОЙ.

1. ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ РИСКА (СТОХАСТИЧЕСКОЙ НЕОПРЕДЕЛЕННОСТИ).

 

Методы принятия решений в играх «с природой» зависят от того, известны или нет вероятности состояний (стратегий) «ПРИРОДЫ» Q.

Принятие решений в условиях риска характеризуется тем, что поведение природы (среды) Q имеет случайный характер. Это проявляется в том, что существует некоторая вероятностная мера, в соответствии с которой возникают (наступают) те или иные состояния Qj природы Q. При этом лицо, принимающее решение, имеет определенную информацию о вероятностях появления состояний Qj «ПРИРОДЫ», которая по своему характеру может быть весьма разнообразна. Например, если имеются три состояния «ПРИРОДЫ» Q1, Q2 и Q3, то дополнительная информация о появлении этих состояний может заключаться в том, что состояние Q1 наименее вероятно, а состояние Q3 наиболее вероятно.

 

Статистические модели принятия решений представляют собой игру двух лиц (человека и природы) с использованием человеком дополнительной статистической информации о состояниях природы.  Создателем теории статистических игр считается А. Вальд. Он показал, что в теории принятия решений статистические игры являются основным подходом, если решение принимается в условиях риска.

Статистическая игра существенно отличается от антагонистической игры двух лиц с нулевой суммой, где выигрыш одного равен проигрышу другого (то есть матричной игры). В статистической игре «ПРИРОДА» не является разумным игро­ком, который стремится выбрать для себя оптимальные стратегии. Этот игрок не заинтересован в выигрыше. Другое дело – человек, в данном случае статистик. Он имеет целью выиграть игру с воображаемым противником, т. е. с ПРИРОДОЙ. Игрок-ПРИРОДА не выбирает оптимальной стратегии, но статистик должен стремиться к определению распределения вероятностей состояния природы.

 

Следовательно, основными отли­чиями статистической игры от стратегической являются:

- отсутствие стремления к выигрышу у игрока-ПРИРОДЫ, т. е. отсутствие антагонистического противника;

- возможность игрока - статистика провести статис­тический эксперимент для получения дополнительной информа­ции о стратегиях природы.

Так, например, статистик, работающий в фирме «Одежда», может изучить многолетние данные о погодных условиях в местностях, где одежда будет продаваться, и в зависимости от наиболее вероятного состояния погоды выработать рекомендации, куда и какое количество партий изделий отправлять, где выгоднее и на каком уровне провести сезонное снижение цен и т. д.

Таким образом, теория статистических решений является теорией проведения статистических наблюдений, обработки этих наблюдений и их использования.

Для принятия решений в условиях риска используют методы теории вероятностей, если это возможно, по причине массовости явления. В таком случае факторы, например, состояния среды представляют собой либо случайные величины, либо случайные функции. Они описываются какими-либо статистическими ха­рактеристиками, например математическим ожиданием и дисперсией, и обладают статистической устойчивостью.

Ситуации, в которых риск связан не с сознательным противодействием противоположной стороны (среды), а с недостаточной осведомленностью о ее поведении или состоянии лица, принимающего решение,  исследуются с помощью теории статистических решений.

 

Пусть события, состоящие в том, что «ПРИРОДА» Q находится в одном из своих состояний Q1, …, Qn,  несовместны  и составляют полную группу событий.   При этом  вероятности pj  состояний «ПРИРОДЫ» Qj известны, то есть известны значения

 

 

где выполнены условия:     

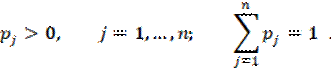
В этом случае мы отступаем от условий полной неопределенности, и будем находиться в ситуации принятия решений в условиях риска.  

 

Рассмотрим «игру с природой» в условиях риска. Пусть у игрока A имеется m возможных стратегий A1, А2, ..., Am,  и можно сделать n предположений о состояниях природы (среды) Q1, Q2, ..., Qn,  с известными вероятностями их появления p1, p2, …, pn, соответственно.

Пусть известен выигрыш aij, i = 1, …, m, j = 1, …, n, который получает игрок A при выборе стратегии Ai для каждого состояния природы Qj.

 

Рассмотрим  вероятностный вектор  p = (p1, p2, …, pn), где элементы pj > 0  - это вероятности соответствующих состояний Qj природы Q.

Тогда можно составить платежную матрицу игры «с природой»  следующего вида:

 

Таким образом, матрица выигрышей игры с «ПРИРОДОЙ» в условиях риска может быть представлена в следующем виде (рис.1)

 

Стратегии игрока A	Состояния природы Q
	p1	…	pj	…	pn
	Q1	…	Qj	…	Qn
A1	a11	…	a1j	…	a1n
…	…	…	…	…	…
Ai	ai1	…	aij	…	ain
…	…	…	…	…	…
Am	am1	…	amj	…	amn

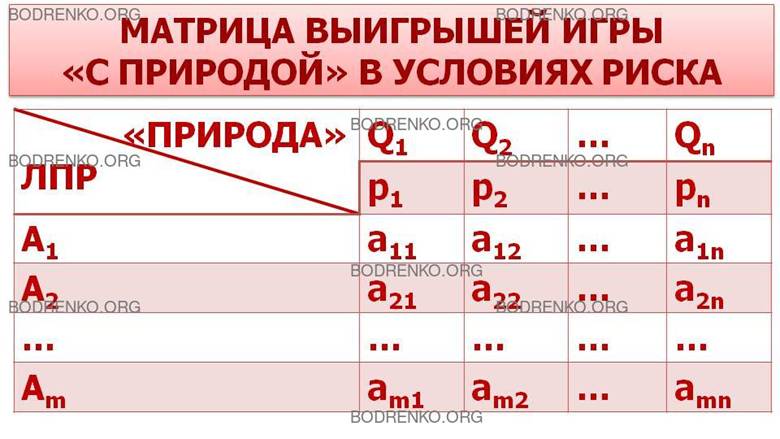
Рис. 1. Платёжная матрица игры «с природой» с вероятностным вектором состояний «природы».  

 

Выбирая стратегию Ai, игрок A знает, что получит один из выигрышей ai1, …, ain с вероятностями p1, …, pn, соответственно. Следовательно, исходом для игрока A  при выборе им стратегии Ai,  является случайная величина

 

 

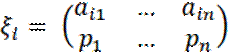
Итак, сравнение двух стратегий Ai и Ak сводится к сравнению соответствующих им случайных величин ξi и ξk.

 

2. КРИТЕРИИ ПРИНЯТИЯ ОПТИМАЛЬНЫХ РЕШЕНИЙ В УСЛОВИЯХ РИСКА.

 

Мы изучим  следующие критерии принятия решений в игре с «природой» в условиях риска (стохастической неопределенности).

 

1. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ (КРИТЕРИЙ МАКСИМУМА ОЖИДАЕМОГО СРЕДНЕГО ВЫИГРЫША).

2. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО РИСКОВ (КРИТЕРИЙ МИНИМУМА ОЖИДАЕМОГО СРЕДНЕГО РИСКА).

3. КРИТЕРИЙ ЛАПЛАСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ (КРИТЕРИЙ «НЕДОСТАТОЧНОГО  ОСНОВАНИЯ» ЛАПЛАСА).

4. КРИТЕРИЙ ЛАПЛАСА ОТНОСИТЕЛЬНО РИСКОВ.

5. КРИТЕРИЙ ХОДЖА-ЛЕМАНА.

6. КРИТЕРИЙ ГЕРМЕЙЕРА.

7. КРИТЕРИЙ ПРОИЗВЕДЕНИЙ С УЧЕТОМ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ «ПРИРОДЫ».

8. МАКСИМАКСНЫЙ КРИТЕРИЙ С УЧЕТОМ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ «ПРИРОДЫ»

9. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С УЧЕТОМ ОТНОСИТЕЛЬНЫХ ЗНАЧЕНИЙ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ ПРИРОДЫ.

10. КРИТЕРИЙ МИНИМИЗАЦИИ СРЕДНЕГО КВАДРАТИЧНОГО ОТКЛОНЕНИЯ (ВАРИАЦИИ).

 

В  случае стохастической неопределенности, когда неуправляемым факторам (состояниям природы) поставлены в соответствие вероятности, заданные экспертно, или вычисленные, решение часто принимается на основе критерия максимума ожидаемого среднего выигрыша (критерий Байеса относительно выигрышей) или минимума ожидаемого среднего риска (критерий Байеса относительно рисков).

 

1. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ.

 (КРИТЕРИЙ МАКСИМУМА ОЖИДАЕМОГО СРЕДНЕГО ВЫИГРЫША).

 

Обозначим показатель эффективности стратегии Аi по критерии Байеса относительно выигрышей через Bi.

 

Для показателя эффективности Bi имеем формулу:

 

 

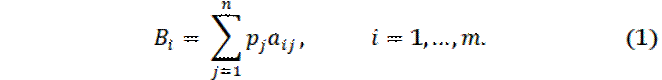
Таким образом, показатель эффективности Bi стратегии Аi по критерию Байеса равен  среднему значению (математическому ожиданию) выигрыша с учетом вероятностей pj всех возможных состояний Qj, j = 1, …, n,  «ПРИРОДЫ» Q.

 

Цена игры по критерию Байеса  (обозначим ее через B) находится по формуле:

 

 

Оптимальной среди чистых стратегий по критерию Байеса является стратегия Ak с максимальным показателем эффективности:

 

Сформулируем правило выбора оптимальных решений в соответствии с критерием Байеса относительно выигрышей. 

 

Матрица выигрышей дополняется ещё одним столбцом с элементами B_i , i = 1, …, m,  – показателями эффективности стратегий A_i  . Действительное  число B_i  равно среднему значению (математическому ожиданию) выигрыша игрока A при применении им стратегии Ai  и определяется по формуле (1). 

Среди всех чистых стратегий A₁,  A₂, …, A_m , необходимо выбрать те стратегии A_k , у которых показатель эффективности B_k  является максимальным (то есть B_k = B, где B определяется по формуле (2)).

 

Таким образом,  решение, выбранное согласно критерию Байеса, является оптимальным не в каждом отдельном случае, а «в среднем».

При этом предполагается, что ситуация, в которой  принимается решение, характеризуется следующими  обстоятельствами:

 

- вероятности появления состояний природы Qj известны и не  зависят от времени;

 

-  решение реализуется (теоретически) бесконечно много раз;

 

- для малого числа реализаций решения допускается  некоторый риск.

 

 

Исходная позиция применяющего критерий Байеса предполагает  более высокий уровень информированности о вероятностях состояний Qj «ПРИРОДЫ» и достаточно длинные реализации. При достаточно большом количестве реализаций среднее значение постепенно стабилизируется. Поэтому при полной (бесконечной) реализации какой-либо риск практически исключен.

 

Рассмотрим  применение критерия Байеса относительно выигрышей на следующем примере.

 

ВЫБОР ОПТИМАЛЬНОГО ВАРИАНТА КАПИТАЛОВЛОЖЕНИЙ ПРИ СТРОИТЕЛЬСТВЕ ЭЛЕКТРОСТАНЦИЙ.

 

Необходимо построить в регионе электростанцию большой мощности. В данном регионе имеются следующие возможности:

- A1 - построение большого водохранилища и гидроэлектростанции;

- A2 - сооружение тепловой электростанции на основном (газовом) топливе и резервном (мазуте);

- A3 - сооружение атомной электростанции.

Игрок A имеет три возможных решения A1, A2, A3. Экономическая эффективность каждого варианта рассчитана проектным институтом, который учитывал затраты на строительство и эксплуатационные расходы.

- На эксплуатационные расходы гидроэлектростанции влияют климатические условия, например, такие, как погодные условия, определяющие уровень воды в водохранилищах.

- Большое число случайных факторов воздействует на экономическую эффективность тепловой станции: цены на мазут и газ, срывы поставок мазута из-за неритмичности работы транспорта в зимнее время, особенно во время снегопадов и продолжительных морозов.

- Экономическая эффективность атомной электростанции будет зависеть от больших затрат на строительство и устойчивости агрегатов и системы управления во время эксплуатации.

 

Таким образом, погодные условия будут в основном сказываться на расходах по эксплуатации гидроэлектростанции и тепловой электростанции. Следовательно, на эффективность тепловой электростанции будут влиять как погодные условия, так и цены на газ и мазут.

 

Случайные факторы, от которых зависит экономическая эффективность вариантов капиталовложений, объединим в четыре возможных состояния природы - Q = (Q1, Q2, Q3, Q4) с учетом окупаемости:

 

Q1 - цены на газ и мазут низкие и климатические условия благоприятные;

Q2 - цены на газ и мазут высокие и климатические условия благоприятные;

Q3 - цены на газ и мазут низкие и климатические условия неблагоприятные;

Q4 – цены на газ и мазут высокие и климатические условия неблагоприятные.

 

Полученные расчеты эффективности капиталовложений при строительстве электростанций приведены в следующей матрице эффективности (рис. 2).

 

 

Состояния «ПРИРОДЫ»   Стратегии игрока A	Q1	Q2	Q3	Q4
A1 - ГИДРОЭЛЕКТРОСТАНЦИЯ	75	75	35	35
A2 – ТЕПЛОВАЯ ЭЛЕКТРОСТАНЦИЯ	60	35	50	30
A3 – АТОМНАЯ ЭЛЕКТРОСТАНЦИЯ	45	45	45	45

Рис. 2. Матрица эффективности.

 

С помощью имеющихся временных рядов можно получить апостериорную информацию, поскольку о влиянии на цены за газ, мазут таких состоянии, как наводнения, засухи, морозы, сильные снегопады и т.п., существует статистическая информация.

По данным многолетней статистики цен и состояний получены оценки апостериорного распределения состояний Qj природы Q.

 

Данные непосредственного наблюдения состояний природы позволили получить апостериорное распределение состояний природы:

 

p1 =  P(Q1) = 0,15;    p2 =  P(Q2) = 0,30;     p3=    Р(Q3) = 0,20; p4 = P(Q4) = 0,35.

 

С учетом вероятностей состояний «ПРИРОДЫ» вычислим показатели эффективности стратегий A1, A2, A3 согласно критерию Байеса.

Получим следующие значения математических ожиданий выигрыша для каждой стратегии игрока A.

 

B1 = p1∙ a11+ p2∙ a12 + p3 ∙a13 + p4 ∙ a14 = 0,15 ∙ 75 + 0,30 ∙ 75 + 0,20 ∙ 35 + 0,35 ∙ 35 = 53;

B2 = p1∙ a21+ p2∙ a22 + p3 ∙a23 + p4 ∙ a24 = 0,15 ∙ 60 + 0,30 ∙ 35 + 0,20 ∙ 50 + 0,35 ∙ 30 = 40;

B3 = p1∙ a31+ p2∙ a32 + p3 ∙a33 + p4 ∙ a34 = 0,15 ∙ 45 + 0,30 ∙ 45 + 0,20 ∙ 45 + 0,35 ∙ 45 = 45;

Цена игры по критерию Байеса равна

B = max {53, 40, 45} = 53.

 

Вывод. В соответствии с критерием Байеса относительно выигрышей оптимальным решением будет инвестирование средств в проект A1 - в строительство гидроэлектростанции.

 

2. Критерий Байеса относительно рисков (критерий минимума ожидаемого среднего риска).

 

Для применения критерий Байеса относительно рисков по исходной платежной матрице строится матрица рисков R = {Rij}(mxn).

 

Показателем эффективности BRi стратегии Ai по критерию Байеса относительно рисков называется математическое ожидание рисков, расположенных в i-й строке матрицы рисков {Rij}:

 

 

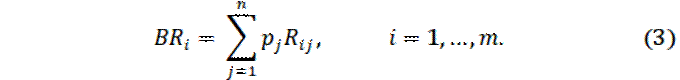
Оптимальной будет стратегия с минимальным значением среднего риска

 

Чистая стратегия Ak  игрока A  будет оптимальной стратегией, если BRk = BR.

 

Сформулируем правило выбора оптимальных решений в соответствии с критерием Байеса относительно рисков (критерий минимума ожидаемого среднего риска). 

Матрица рисков дополняется ещё одним столбцом с элементами BR_i , i = 1, …, m,  – показателями эффективности стратегий A_i  . Действительное  число BR_i  равно среднему значению (математическому ожиданию) риска  игрока A при применении им стратегии Ai  и определяется по формуле (3). 

Среди всех чистых стратегий A₁,  A₂, …, A_m , необходимо выбрать те стратегии A_k , у которых показатель эффективности BR_k  является минимальным (то есть BR_k = BR, где BR определяется по формуле (4)).

 

При этом справедливо утверждение о том, что критерии Байеса относительно выигрышей и относительно рисков эквивалентны, то есть по обоим критериям оптимальной будет одна та же стратегия.

 

Рассмотрим применение критерия минимума ожидаемого среднего риска на следующем примере.

 

 

 

На промышленном предприятии готовятся к переходу на выпуск новых видов продукции A1, A2 , A3 , A4 . Результаты принятых решений существенно зависят от степени обеспеченности производства материальными ресурсами Q1 , Q2 , Q3 .

 

Каждому сочетанию (Ai, Qj) решений A i , i = 1,2, 3, 4,  и состояний среды Qj , j = 1,2,3, соответствует определенный выигрыш  aij –  эффективность выпуска новых видов продукции. Всевозможные выигрыши представлены в матрице эффективности (рис. 3):

 

Состояния «ПРИРОДЫ»   Стратегии игрока A	Q1	Q2	Q3
A1	35	45	50
A2	80	30	40
A3	45	95	30
A4	90	20	45

Рис. 3. Матрица эффективности выпуска новых видов продукции.

 

Найдем оптимальную стратегию игрока A в предположении, что известны вероятности состояний «ПРИРОДЫ»: p1= 0,15; p2 = 0,35, p3 = 0,5.  

 

Построим матрицу рисков для данной игры «с природой» (рис. 4). Мы имеем

 

Состояния «ПРИРОДЫ»   Стратегии игрока A	Q1	Q2	Q3
A1	R11 = 55	R12 =  50	R13 =   0
A2	R21=  10	R22 =  65	R23 = 10
A3	R31=  45	R32 =    0	R33=  20
A4	R41=    0	R42 =  75	R43 =   5

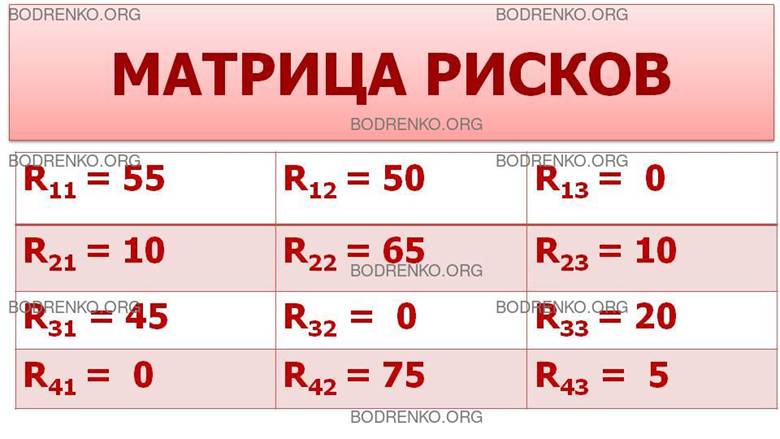
Рис. 4. Матрица рисков.

 

Находим ожидаемые средние риски игрока A.

 

BR1 = p1∙ R11+ p2∙ R12 + p3 ∙R13 = 0,15 ∙ 55 + 0,35 ∙ 50 + 0,50 ∙ 0  = 25,75;

BR2 = p1∙ R21+ p2∙ R22 + p3 ∙R23 = 0,15 ∙ 10 + 0,35 ∙ 65 + 0,50 ∙ 10 = 29,25;

BR3 = p1∙ R31+ p2∙ R32 + p3 ∙R33 = 0,15 ∙ 45 + 0,35 ∙ 0 + 0,50 ∙ 20 = 16,75;

BR4 = p1∙ R41+ p2∙ R42 + p3 ∙R43 = 0,15 ∙ 0 + 0,35 ∙ 75 + 0,50 ∙ 5 = 28,75;

BR = min {25,75; 29,25; 16,75; 28,75} = 16,75.

 

Вывод. В соответствии с критерием Байеса относительно рисков оптимальным решением будет стратегия A3.

 

Замечание.  По критерию Байеса относительно выигрышей показатели эффективности Bi стратегий Ai  имеют следующие значения: B1 = 46;  B2= 42,5;   B3 = 55;  B4 = 43.

 

Следовательно, цена игры

B = max {46; 42,5; 55; 43} = 55.

Значит, оптимальной является стратегия A3.

 

3. Критерий Лапласа относительно выигрышей (критерий «недостаточного основания»)

 

В предыдущих двух критериях Байеса известные вероятности состояний природы могли быть получены, например, на основании статистических исследований. Однако часто складывается такая ситуация, при которой мы лишены возможности определить эти вероятности. Но, желая принять решение в условиях риска, мы вынуждены оценивать эти вероятности состояний природы субъективно.

Существуют различные методы численной субъективной оценки степени правдоподобности состояний природы. Один из таких способов заключается в том, что мы считаем состояния природы Qj равновероятными: p1 = p2 = ... = pn = 1/n. То есть мы не можем отдать предпочтение ни одному из состояний Qj «ПРИРОДЫ» Q. Этот принцип называют еще принципом «недостаточного основания» Лапласа.

 

Таким образом, показатель эффективности Li стратегии Ai будет равен:

Li = 1/n ∑ aij,

 

Цена игры по критерию Лапласа равна

L = max Li.

 

Оптимальная стратегия Ak определяется по формуле: Lk = L.

 

Найдем  оптимальную стратегию в условиях по критерию Лапласа для игры «с природой», заданной матрицей эффективности (рис. 3).

 

Решение. Вычислим средние выигрыши:

 

L1 = 1/3(35+45+50) = 130/3;

L2 = 1/3 (80+30+40) = 150/3;

L3 = 1/3 (45+95+30) = 170/3;

L4 = 1/3 (90+20+45) = 155/3.

Следовательно, оптимальной по критерию Лапласа является стратегия A3, так как показатель эффективности L3 = max Li.

 

4. Критерий Лапласа относительно рисков.

Для применения критерий Лапласа относительно рисков по исходной платежной матрице строится матрица рисков R = {Rij}(mxn).

 

Показателем эффективности LRi стратегии Ai по критерию Лапласа относительно рисков называется среднее значение рисков, расположенных в i-й строке матрицы рисков {Rij}:

 

 

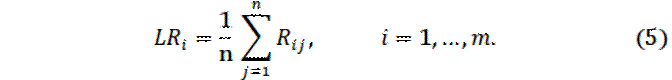
Оптимальной будет стратегия с минимальным значением среднего риска

 

Чистая стратегия Ak  игрока A  будет оптимальной стратегией, если LRk = LR.

Найдем  оптимальную стратегию в условиях по критерию Лапласа относительно рисков для игры «с природой», заданной матрицей эффективности (рис. 3).

 

Решение. Вычислим средние риски:

 

LR1 = 1/3(55+50+0) = 105/3;

LR2 = 1/3 (10+65+10) = 85/3;

LR3 = 1/3 (45+0+20) = 65/3;

LR4 = 1/3 (0+75+5) = 80/3.

Вывод: оптимальной стратегией по критерию Лапласа относительно рисков является стратегия A3.

 

5. КРИТЕРИЙ ХОДЖА-ЛЕМАНА.

 

Этот критерий опирается одновременно на критерий Вальда и критерий Байеса.

 

Пусть Wi = min aij - показатель эффективности  стратегии Аi по критерию Вальда.

           

Пусть Bi  - показатель эффективности стратегии Аi по критерию Байеса.

 

Показатель эффективности стратегии Ai по критерию Ходжа-Лемана определяется по формуле:

 

HLi = (1-h) Wi + h Bi, где 0≤  h ≤ 1.

То есть показатель эффективности HLi чистой стратегии Аi равен:

 

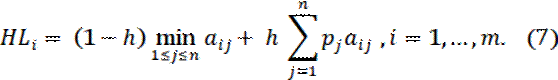
В правой части формулы (7) коэффициент h есть количественный показатель степени доверия игрока А  данному распределению вероятностей pj= p(Qj), j=1,…,n, состояний природы Qj, j=1,…,n, а коэффициент (1 – h) характеризует количественно степень пессимизма игрока А.

Чем больше доверия игрока А данному распределению вероятностей состояний природы, тем меньше пессимизма и наоборот. Если доверие велико, то доминирует критерий Байеса, в противном случае – критерий Вальда.

 

Цену игры HL по критерию Ходжа-Лемана находим по формуле:

 

HL = max HLi

 

Оптимальной стратегией по критерию Ходжа-Лемана является стратегия Аk с наибольшим показателем эффективности:

 

HLk= HL.

Отметим, что критерий Ходжа-Лемана является как бы промежуточным критерием между критериями Байеса и Вальда.

 

При h =1, из (7) имеем: HLi=Bi,  и потому критерий Ходжа-Лемана

превращается в критерий Байеса.

А при h =0, из (7): HLi=Wi,  и, следовательно, из критерия Ходжа-Лемана получаем

критерий Вальда.

 

Выбор параметра h субъективен,  так как  определить степень достоверности какой-либо функции распределения довольно сложно.

 

Для применения критерия Ходжа - Лемана желательно, чтобы ситуация в которой принимается решение, удовлетворяла свойствам:

 

- вероятности появления состояния Qj неизвестны, но некоторые предположения о распределении вероятностей возможны;

 

- принятое решение теоретически допускает бесконечно много реализаций;

 

- при малых числах реализации допускается некоторый риск.

 

6. КРИТЕРИЙ ГЕРМЕЙЕРА.

 

Показатель эффективности GWi стратегии Аi по критерию Гермейера определяем по формуле

 

GWi =  min pj aij (8)

 

Если игрок А придерживается стратегии Аi, то вероятность выигрыша aij при этой стратегии и при состоянии природы Qj равна, очевидно, вероятности pj этого состояния природы. Поэтому формула (8) показывает, что показатель эффективности GWi стратегии Аi по критерию Гермейера есть минимальный выигрыш при этой стратегии с учетом его вероятности.

Цена игры по критерию Гермейера определяется по формуле:

 

GW = max GWi

 

Оптимальной стратегией по критерию Гермейера считается стратегия Аk с наибольшим показателем эффективности:

 

GWk= GW.

Матрица Гермейера.

Умножая каждый выигрыш aij, i = 1, …, m, на вероятность pj состояния природы Qj получим элементы матрицы Гермейера: элемент gij = pj · aij, i = 1, …, m, j = 1, …, n.

Из элементов gij формируем матрицу Гермейера G.

 

Состояния «природы» Стратегии игрока A	Q1	Q2	…	Qn
	p1	p2	…	pn
A1	G11 = p1 a11	G12 = p2 a12	…	G1n = pn a1n
A2	G 21 = p1 a21	G22 = p2 a22	…	G2n = pn a2n
…	…	…	…	…
Am	Gm1 = p1 am1	Gm2 = p2 am2	…	Gmn = pn amn

Рис. 4. Матрица Гермейера G.

 

С учетом введенных обозначений  числа Gi = min gij, (j = 1,..., n) являются показателями эффективности стратегии Aj по критерию Гермейера.  Таким образом, критерий Гермейера можно интерпретировать как критерий Вальда, применимый к игре с «ПРИРОДОЙ» с матрицей Гермейера Gij (mxn).

 

Критерий Гермейера так же,как и критерий Вальда является критерием крайнего пессимизма игрока А, но, в отличие от критерия Вальда, игрок А, принимая решение с максимальной осмотрительностью, учитывает вероятности состояний природы.

 

Условия  применимости критерия Геймейера таковы:

 

- вероятности появления состояний Qj известны;

- с появлением тех или иных состояний Qj, отдельно или в комплексе, необходимо считаться;

- допускается некоторый риск;

- решение может реализоваться один или много раз.

 

Если функция распределения известна не очень надежно, а числа реализаций малы, то, следуя критерию Геймейера, получают, вообще говоря, неоправданно большой риск. Таким образом, здесь остается некоторая свобода для субъективных действий.

 

В случае равномерного распределения вероятностей состояний природы: pj=1/n,  j=1,…,n, показатель эффективности стратегии Аi, в силу формулы (*), будет равен

 

GWi= 1/n min aij.

 

Следовательно, критерий Гермейера в этом случае эквивалентен критерию Вальда.

То есть стратегия, оптимальная по критерию Гермейера, в случае, когда мы считаем  все состояния природы Qj равновероятными, оптимальна и по критерию Вальда, и наоборот.

 

7. КРИТЕРИЙ ПРОИЗВЕДЕНИЙ (С УЧЕТОМ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ «ПРИРОДЫ»).

 

Пусть матрицей выигрышей игрока А является матрица А, все элементы которой положительны: aij>0, i=1,…, m; j=1,…, n.

 

Известны вероятности pj=p(Qj), j=1,…,n, состояний природы Qj, j=1,…, n, и удовлетворяют условию (1).

 

Показатель эффективности стратегии Аi по критерию произведений (с учетом вероятностей состояний «природы») определим по формуле:

 

PGi = ∏ pj aij = ∏ gij , где gij — элемент матрицы Гермейера.

 

Цена игры по критерию произведений вычисляется по формуле:

 

PG = max PGi

 

Оптимальной стратегией по критерию произведений является стратегия Аk с наибольшим показателем эффективности:

 

PGk=PG.

Отметим, что для критерия произведений является существенным положительность всех состояний вероятностей состояний природы и всех выигрышей игрока А.

 

8. МАКСИМАКСНЫЙ КРИТЕРИЙ С УЧЕТОМ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ «ПРИРОДЫ».

 

Теперь опишем максимаксный критерий, применяемый к матрице Гермейра, который для краткости будем называть MG-критерием. Максимаксный критерий, применяемый к матрице Гермейера можно назвать максимаксным критерием с учетом вероятностей

 состояний «ПРИРОДЫ».

 

Наибольший элемент в i-й строке матрицы Гермейра G

MGi = max gij (j=1, …, n) 

назовем показателем эффективности стратегии Ai по MG-критерию

 

(или MG-показателем эффективности стратегии Ai ).

 

Наибольший из MG-показателей эффективности стратегий

 

MG = max MGi (i = 1, …, m)

назовем ценой игры по MG-критерию (или MG-ценой игры).

 

Получим

MG  = max  max gij (9)

В соответствии с этим равенством M-цену игры можно назвать

 

также максимаксом матрицы Гермейера G.

 

Из равенства (9) очевидно, что MG-цена игры является максимальным элементом среди всех элементов матрицы Гермейера G.

 

Оптимальной по MG-критерию назовем стратегию Ak , MG-показатель эффективности которой совпадает с MG-ценой игры: MGk =  MG.

Каждая стратегия, в соответствующей строке матрицы Гермейера G которой стоит максимальный элемент, будет MG-оптимальной.

 

 

9. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С УЧЕТОМ ОТНОСИТЕЛЬНЫХ ЗНАЧЕНИЙ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ ПРИРОДЫ.

 

Предположим, что вероятности состояний природы нам неизвестны, но мы имеем представление о том, какие состояния природы более правдоподобны, какие — менее правдоподобны. Это позволит представить (проранжировать) неизвестные вероятности состояний природы в виде убывающей или возрастающей числовой последовательности.

 

Например, можно считать, что последовательность неизвестных вероятностей pj состояний природы Qj пропорциональна членам некоторой монотонной последовательности положительных чисел t1 ,  t2 , ..., tn :

 

p1 : p2 : ... : pn = t1 : t2 : ... : tn .

 

Учитывая, что

 

 

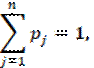
можем получить следующие оценки вероятностей:

 

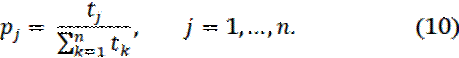
ПРИМЕР.

Найдем оптимальную стратегию в условиях (рис. 3),  если есть основания считать, что вероятности состояний природы образуют строго убывающую числовую последовательность, пропорциональную убывающей арифметической прогрессии 3, 2, 1, то есть:

 

p 1 : p 2 : p 3 = 3 : 2 : 1 .

 

Решение. Вычислим оценки вероятностей состояний природы по формуле (10):

 

p 1 =  1/2, p 2 = 1/3 , p 3 = 1/6.

 

Тогда средние выигрыши Vi будут равны:

 

V1 = 35/2 + 45/3 + 50/6 = 245/6;

V2 = 80/2 + 30/3 + 40/6 = 340/6;

V3 = 45/2 +  95/3 + 30/6 = 355/6;

V4 = 90/2 + 20/3 + 45/6 =  355/6.

Следовательно, игроку A можно порекомендовать сделать выбор между стратегиями А3 и A4 с максимальными средними выигрышами.

 

Аналогичный критерий можно рассмотреть и для матрицы рисков.

 

10. КРИТЕРИЙ МИНИМИЗАЦИИ СРЕДНЕГО КВАДРАТИЧНОГО ОТКЛОНЕНИЯ В УСЛОВИЯХ РИСКА. 

 

При принятии решений в условиях риска можно применить и критерий, основанный на применении среднего квадратичного отклонения — критерий минимизации среднего квадратичного отклонения (вариации).

 

Вычислим математические ожидания выигрышей игрока A при применении им чистой стратегии Ai.

 

B1 = p1∙ a11+ p2∙ a12 + p3 ∙a13 = 0,15 ∙ 35 + 0,35 ∙ 45 + 0,50 ∙ 50  = 46;

B2 = p1∙ a21+ p2∙ a22 + p3 ∙a23 = 0,15 ∙ 80 + 0,35 ∙ 30 + 0,50 ∙ 40 = 42,5;

B3 = p1∙ a31+ p2∙ a32 + p3 ∙a33 = 0,15 ∙ 45 + 0,35 ∙ 95 + 0,50 ∙ 30 = 55;

B4 = p1∙ a41+ p2∙ a42 + p3 ∙ a43 = 0,15 ∙ 90 + 0,35 ∙ 20 + 0,50 ∙ 45 = 43;

Следовательно, по критерию Байеса предпочтения игрока A можно проранжировать так:

 

A 3 » A 1 » A 4 » A 2 .

 

Вычислим средние квадратичные отклонения выигрышей:

S1 ² = 35 ² × 0,15 + 45 ² × 0,35 + 50 ² × 0,5 – (46) ² = 2142,5 – 2116  = 26,5 ;  S1 ≈ 5,15;

 

S2 ² = 80 ² × 0,15 + 30 ² × 0,35 + 40 ² × 0,5 –  (42,5) ² = 2075 – 1806,25  = 268,75 ,  S2 ≈ 16,4;

 

S3 ² = 45 ² × 0,15 + 95 ² × 0,35 + 30 ² × 0,5   – (55) ² = 3912,5 –3025 = 887,5,  S3 ≈ 29,8;

 

S4 ² = 90 ² × 0,15 + 20 ² × 0,35 + 45 ² × 0,5  –  (43) ² = 2367,5  – 1849 = 518,5 ,   S4 ≈ 22,77.

Таким образом, по критерию минимизации среднего квадратичного отклонения, получаем:

 

A1   »  A 2  »  A 4  »  A 3 .

То есть наиболее предпочтительной является стратегия A 1 с наименьшим значением (5,15) среднего квадратичного отклонения.

 

Данная ситуация наиболее характерна для задач принятия решений, когда стратегия, наиболее предпочтительная по критерию максимизации среднего выигрыша, наименее выгодна по критерию минимизации среднего квадратичного отклонения.

 

Таким образом, в данных условиях  игроку A предстоит сделать выбор между двумя стратегиями A1 и A3 , один из которых ( A 3 ) характеризуется и большим средним выигрышем и большим риском одновременно.

 

В этом случае можно порекомендовать использование особой меры риска — коэффициента вариации:

 

CV ( Ai ) = CVi = (Si/Bi) x 100 % .

Этот коэффициент отражает риск, который приходится на единицу выигрыша (доходности), и дает базу для сравнения стратегий игрока, когда и их средний выигрыш и их средний риск неодинаковы.

 

В данных условиях можно получить:

 

CV1 = (5,15/46) x 100 % = 11,2 % ;

 

CV2 = (16,4/42,5) × 100 % =  38,6 % ;

 

CV3 = (29,8/55) x 100 % = 54,2 % ;

 

CV4  = (22,77/43) x 100 %  = 53 % .

 

Следовательно, по критерию минимизации коэффициента вариации, предпочтения игрока можно проранжировать так:

 

A 1 »  A 2 »  A 4 »  A 3.

 

То есть наиболее предпочтительной является стратегия A1 .

 

Заметим также, что когда речь идет о среднем выигрыше, то речь идет о возможности многократного повторения игры (акта принятия решений). И условность рассмотренных выше критериев состоит в том, что требуемого количества повторений чаще всего может и не быть.

 

3. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА В ИГРАХ С ПРИРОДОЙ.

При принятии решений в условиях неопределенности существенную помощь может оказать эксперимент, цель которого: уточнить условия в определенной ситуации. Проблема заключается в том, что проведение эксперимента предполагает наличие  определенных затрат. Целесообразность эксперимента определяется корреляцией между суммой  необходимых затрат на его проведение и величиной ожидаемого выигрыша.

Рассмотрим, имеет ли смысл предпринимать эксперимент «Кси» для уточнения условий в некоторой ситуации.   

Рассмотрим теперь вопрос о том, в каких случаях следует проводить эксперименты с целью получения дополнительной статистической информации о состояниях природы для принятия более эффективных решений в условиях риска.

 

Случай 1. Рассмотрим сначала так называемый «идеальный» эксперимент Ω, в результате проведения которого игрок получает точную информацию о том, какое состояние природы будет иметь место в данной ситуации. В качестве критерия принятия решений рассмотрим критерий Байеса.

Без проведения эксперимента Ω в качестве оптимальной стратегии по критерию Байеса относительно выигрышей выбиралась стратегия Ak  с максимальным показателем эффективности  

Bk = B.

Если в результате проведенного эксперимента Ω  выяснилось, например, что природа будет находиться в состоянии Qj , то в качестве оптимальной надо выбирать стратегию Ai, при которой достигается максимальный выигрыш: βj = max a ij , где i = 1, …,  m.

где βj , j = 1, …,  n — показатель благоприятности состояния природы Qj.

 

То есть надо выбирать такую стратегию, чтобы наибольший элемент βj j-го столбца матрицы A находился в строке, соответствующей этой стратегии. Однако такое решение мы можем принять только после проведения эксперимента Ω .

А нам нужно решить заранее вопрос о целесообразности проведения эксперимента Ω , про который известно только, что он является идеальным, и неизвестно, в каком именно состоянии Q j будет находиться природа Q, то есть нам не известен размер будущего выигрыша игрока A.

 

Таким образом, разумно рассмотреть взвешенное среднее выигрышей βj с весовыми коэффициентами pj , то есть выигрыш в случае идеального эксперимента Ω  можно определить так:

 

β = ∑ pj ∙ βj.

 

Из математического  ожидания среднего выигрыша вычтем стоимость C эксперимента Ω  и получим средний выигрыш с проведением идеального эксперимента: β - С. Без проведения идеального эксперимента Ω  средний выигрыш равен В.

Тогда средний выигрыш игрока A с применением идеального эксперимента Ω вырастет на величину β - B.

Таким образом, проведение эксперимента Ω имеет смысл, если β – С < B.  Следовательно, стоимость C такого эксперимента удовлетворяет условию:

 

C <  β – B (11).

 

 

Определим стоимость С идеального эксперимента Ω  в условиях (рис. 3).

 

Решение. Вычислим показатели благоприятности состояний природы:

 

β1 = 90 ;  β2 = 95 ;  β3 = 50.

 

Тогда

 

β = 90 × 0,15 + 95 × 0,35 + 50 × 0,5 = 71,75.

 

Так как B = 55 , то стоимость C эксперимента  Ω  будет меньше, чем

 

С < β – B = 71,75 – 55 = 16,75 ед.

 

То есть, если стоимость эксперимента С ≥ 16,75 ед., то эксперимент Ω проводить невыгодно.

 

Можно решить эту задачу и в терминах рисков, а именно:

Рассмотрим неравенство C <  β – B

β – B =  ∑ pj ∙ βj – max ∑ pj ∙ aij

 

Тогда С < min (∑ pj (βj -  aij)) = min ∑ pj Rij = R0.

 

Таким образом, стоимость эксперимента C в терминах рисков удовлетворяет условию:

 

С < R0 = min ∑ pj Rij

 

При этом получаются те же самые результаты, что и по условию (11).

Таким образом, правило решения о проведении эксперимента Ω  приобретает следующий вид.

Эксперимент Ω надо проводить, если затраты C на его осуществление меньше  минимального среднего риска  R0: C < R0.

В противном случае от эксперимента следует воздержаться и применить ту стратегию Ak, для которой достигается минимум среднего риска.

 

Случай 2. Теперь рассмотрим вопрос о проведении эксперимента, не являющегося идеальным, то есть позволяющего лишь уточнить вероятности состояний природы.

«Неидеальный эксперимент» не приводит к выяснению в точности состояния природы Qj, но дает косвенные сведения в пользу того или иного состояния природы. В общем случае можно предположить, что такой эксперимент Z приводит к появлению одного из несовместных событий Zr , r = 1, …, k (исходов эксперимента), вероятности которых зависят от того состояния природы Q j , при котором он проводился.

 

Предположим, что эти условные вероятности p P (Zr |Qj) событий Z = Zr, при условии, что природа находится в состоянии Q = Qj , известны.

Таким образом, исходными данными для «неидеального» эксперимента являются:

- матрица выигрышей A = {aij}(m x n);

- «априорные» вероятности pj состояний природы Qj, j = 1, …, n;

- матрица условных вероятностей {P (Zr|Qj)} = {Prj}(k x n);

- затраты C  на проведение «неидеального» эксперимента Z.

 

Пусть «неидеальный» эксперимент Z дал исход Zr.

После проведения эксперимента, давшего исход Zr, где 1≤ r ≤ k, необходимо пересчитать вероятности состояний природы Qj при условии, что эксперимент Z дал исход Zr.

То есть необходимо вычислить  p j|r = P (Qj |Zr) — «апостериорные» вероятности состояний природы Qj, при условии, что результатом эксперимента будет Z = Zr;

 

Применим формулу Байеса для условных вероятностей и пересчитаем вероятности состояний природы Qj:

 

P (Q | Z) =[P (Q) × P ( Z |Q )]/   P(Z)

 

или

 

p j|r = P (Q=Q j | Z=Zr) =  [P (Q = Qj) × P(Z =Zr | Q = Qj)]/ P (Z = Zr),

 

где P (Q = Qj) = pj — «априорные» вероятности состояний природы Qj;

Вычислим по формуле полной вероятности

 

P (Z = Zr) =  ∑ P(Q = Qj) × P (Z = Zr |Q = Qj) (12).

где суммирование по j = 1, …, n.

 

Вероятности P (Z = Zr) — вероятности исхода Zr эксперимента.

Поскольку «априорные» вероятности pj состояний природы Qj после эксперимента, давшего исход Zr, заменяются «апостериорными» вероятностями pj|r, то показатели эффективности стратегии Ai по критерию Байеса необходимо пересчитать.

Вычислим показатель эффективности стратегии A i по критерию Байеса с «апостериорными вероятностями» p j|s состояний Qj природы  Q:

 

B i|r = ∑ p j|r ∙ aij,  i = 1, …,  m , где  1 ≤ r ≤  k.  

Пусть  D r – максимальный средний выигрыш после проведения эксперимента, давшего исход Zr:    

D r = max B i|r (i= 1, …, m).

 

Обозначим D  =  ∑ P ( Z = Zr) × Dr — среднее взвешенное максимальных выигрышей Dr с весовыми коэффициентами, равными полным вероятностям P (Z = Zr) событий Zr, вычисляемым по формулам (12).

 

Без проведения «неидеального» эксперимента Z в качестве оптимальной стратегии по критерию Байеса относительно выигрышей выбиралась стратегия Ai  с максимальным показателем эффективности 

Bi = B.

 

Тогда средний выигрыш игрока A с применением «неидеального» эксперимента вырастет на величину D  – B.

Таким образом, проведение эксперимента имеет смысл, если стоимость такого эксперимента C удовлетворяет условию:

 

C < D  – B

МОЖНО РЕШИТЬ ЭТУ ЗАДАЧУ И В ТЕРМИНАХ РИСКОВ. ПРИ ЭТОМ РЕЗУЛЬТАТ ОЦЕНКИ СТОИМОСТИ ЭКСПЕРИМЕНТА  НЕ ИЗМЕНИТСЯ.

 

Мы рассмотрели вопрос о том — выгодно, или невыгодно проводить единичный эксперимент. Аналогичным образом можно заранее выяснить, выгодно ли провести эксперимент несколько раз.

 

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Дубров А.М.,  Лагоша Б.А., Хрусталев Е.В. Моделирование рисковых ситуаций в экономике и бизнесе.- М.: Финансы и статистика, 2000. – 176 с. 

[2]  Колобашкина Л.В., Алюшин М.В. Информационные технологии принятия решений в условиях конфликта. Учебное пособие для вузов. В двух частях. Часть I. Основы теории игр. - М.: НИЯУ МИФИ, 2010. – 164 с.

[3]  Мушик Э., Мюллер П. Методы принятия технических решений: Пер. с нем. – М.: Мир, 1990. – 208 с., ил.

[4]  Садовин Н.С., Садовина Т.Н. Основы теории игр. Учебное пособие. – Йошкар-Ола, 2011. – 119 с.

[5]  Шапкин А.С., Шапкин В.А. Теория риска и моделирование рисковых ситуаций. Учебник. - М.: Издательско-торговая корпорация «Дашков и К⁰», 2005. - 880 с.