Методы принятия управленческих решений. Экспертные методы принятия решений. Метод экспертных оценок. Метод Дельфи. Отбор экспертов и организация их работы. Анализ согласованности оценок экспертов. Метод ранговой корреляции Спирмена. Коэффициент конкордации Кендалла. Открытый вопрос. Закрытый вопрос. Ранжирование
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Методы принятия управленческих решений
Лекция
4
Тема
лекции 4: «Экспертные методы принятия решений»

Разделы лекции:
1. Метод экспертных оценок. Метод
Дельфи.
2. Отбор экспертов и организация их
работы.
3. Анализ согласованности оценок
экспертов.

РАЗДЕЛ 1. МЕТОД ЭКСПЕРТНЫХ ОЦЕНОК. МЕТОД ДЕЛЬФИ.
ИСПОЛЬЗОВАНИЕ «МЕТОДОВ ЭКСПЕРТНЫХ
ОЦЕНОК».
Использование информации, полученной от
специалистов, особенно плодотворно, если для ее сбора, обобщения и анализа
применяются специальные логические приемы и математические методы – методы
экспертных оценок. Экспертный метод в значительной мере может обеспечить
объективность, многосторонность, комплексность и компетентность принимаемых
практических решений. На сегодня этот метод достаточно разработан и применяется
у нас и за рубежом как средство повышения надежности решения научных и
управленческих проблем. Однако следует помнить, что он не должен быть
единственным основанием для принятия решений и должен сопровождаться
сопоставлением с объективной информацией, полученной другими методами.
При решении сложных проблем один
специалист не в состоянии учесть все факторы и взаимосвязи между ними или
оценить вероятности большого числа альтернатив. Поэтому групповые экспертизы
получили широкое распространение. Преимуществом их является возможность разностороннего анализа
количественных и качественных аспектов сложных проблем. Примером таких проблем
являются прогнозы в области политики, науки и техники, для обоснования которых
нет адекватной информации.
При использовании мнений группы
специалистов предполагается, что взаимодействие между ними позволит
скомпенсировать смещение оценок отдельных членов группы и что сумма информации,
имеющейся в распоряжении группы экспертов, будет больше, чем информация любого
члена группы. Очевидно также, что сумма факторов, которые имеют отношение к
данной проблеме и могут быть рассмотрены группой экспертов, как правило, больше
или, по крайней мере, так же велика, как сумма факторов, которые может учесть
отдельный эксперт.
В общем случае мнение группы экспертов
надежнее, чем мнение отдельного индивида, а две группы одинаково компетентных
экспертов с большей вероятностью дадут аналогичные ответы на ряд вопросов, чем
два индивида. Предполагается также, что интервал оценок, полученных от группы экспертов,
включает в себя «истинную» оценку. Эти предположения не очевидны, особенно если
учесть проблемы групповой динамики. К примеру, мнения специалистов, даже
работающих в одной узкой области, могут расходиться. Более того, и
однозначность ответов не является гарантией их обоснованности. Во всяком
случае, нет способа проверить это в момент проведения экспертизы. Можно
предположить, что взятое наудачу мнение любого из экспертов будет так же
достоверно, как и групповая оценка, поскольку никто не может заранее сказать,
каков «истинный» результат. В то же время основное преимущество групповой
оценки заключается в уменьшении различий во мнениях, в возможности получения
более обобщенного, более представительного мнения. Сочетание индивидов,
обладающих разными стилями мышления, несомненно, позволяет повысить надежность
решения задач. В то же время, очевидно,
что количество неверной информации у группы экспертов будет больше или, по крайней мере, такое же, как и у одного из них. Немалое
влияние на надежность решений может оказывать также групповой конформизм.
Экспериментально установлено, что,
несмотря на эти недостатки, групповые оценки более надежны, чем индивидуальные,
при условии соблюдения определенных требований, важнейшими из которых являются:
а) приемлемое «гладкое» распределение
оценок, полученное от экспертов, указывающее на независимость их мнений. В
случае многомодального распределения должна быть установлена причина, по
которой различные эксперты по-разному интерпретируют одну и ту же проблему;
б) групповая надежность, означающая,
что две групповые оценки по определенной проблеме, данные двумя одинаковыми
подгруппами, выбранными случайным образом, будут близкими. Корреляция по ряду
таких оценок должна быть высокой.
ЧТО ТАКОЕ «ЭКСПЕРТНАЯ ОЦЕНКА»?
Экспертные оценки – это качественные оценки, основанные
на информации неколичественного (качественного) характера, которые могут быть
получены только с помощью специалистов – экспертов. Эксперт – это
высококвалифицированный специалист, полагающийся на свои знания, опыт, интуицию
и умение оценивать сложные факторы (явления) и способный создать собственную
обоснованную (интуитивную) модель анализируемого явления (проблемы), если он
располагает необходимой для этого исходной информацией.
В ЧЕМ СОСТОИТ СУЩНОСТЬ МЕТОДА ЭКСПЕРТНОГО
ОЦЕНИВАНИЯ?
Метод экспертного оценивания
относится к инструментарию количественной оценки качества альтернатив в
условиях слабоформализуемой проблемной ситуации. Сущность метода экспертных
оценок заключается в логико-интуитивном анализе внутренней и внешней среды
организации, разработке альтернатив и количественной оценке их качества.
Обобщенное мнение экспертов служит основанием для осуществления выбора.
КАКИЕ ТИПОВЫЕ ЗАДАЧИ РЕШАЮТСЯ МЕТОДОМ
ЭКСПЕРТНОГО ОЦЕНИВАНИЯ?
Методом экспертного оценивания решаются
следующие типовые задачи:
1) определение состава возможных
событий в какой-либо системе в определенном интервале времени;
2) определение вероятностей событий и
временных интервалов во множестве событий;
3) структурирование проблемного поля
организации и определение приоритетности решения проблем;
4) дифференциация целей управления до
задач и определение приоритетности их решения;
5) генерирование альтернатив;
6) фильтрация множества альтернатив и
оценка их предпочтительности.
ЧТО ТАКОЕ ЭКСПЕРТНЫЕ СУЖДЕНИЯ?
Экспертные суждения – содержательные высказывания (определяющие
состав, структуру, функциональность исследуемой системы, сущностей и их
атрибутов), количественная или качественная оценка какой-либо сущности (т.е.
определение количественных и качественных атрибутов и их значений).
В ЧЕМ ЗАКЛЮЧАЕТСЯ СУЩНОСТЬ ЭКСПЕРТНОГО
РАНЖИРОРАНИЯ?
Экспертное ранжирование применяется в
случаях, когда невозможна или нецелесообразна непосредственная оценка. При этом
ранжирование объектов содержит лишь информацию о том, какой из них более
предпочтителен, и не содержит информации о том, насколько или во сколько раз один
объект предпочтительнее другого.
Ранг – степень отличия по какому-либо
признаку, а ранжирование – процесс
определения рангов, относительных количественных оценок степеней отличий по
качественным признакам.
КАКИЕ ОСНОВНЫЕ МЕТОДЫ РАНЖИРОВАНИЯ
ИСПОЛЬЗУЮТСЯ?
Используются следующие основные методы
ранжирования: МЕТОД ПРОСТОЙ РАНЖИРОВКИ; МЕТОД НЕПОСРЕДСТВЕННОЙ ОЦЕНКИ; МЕТОД
ПАРНЫХ СРАВНЕНИЙ, МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРЕДПОЧТЕНИЙ.
В ЧЕМ ЗАКЛЮЧАЕТСЯ МЕТОД ПРОСТОЙ
РАНЖИРОВКИ?
При решении многих практических задач
часто оказывается, что факторы, определяющие конечные результаты, не поддаются
непосредственному измерению. Расположение этих факторов (альтернатив) в порядке
возрастания или убывания какого-либо присущего им свойства называется
ранжированием. Нередко рассматриваемые явления имеют различную природу и в
связи с этим несоизмеримы. В этих случаях установление их относительной
значимости с помощью экспертов и присвоение чисел натурального ряда,
определяющих порядок (место) каждого явления в исследуемой совокупности,
облегчает выбор наиболее предпочтительной из альтернатив.
Метод простой ранжировки заключается в
том, что эксперты располагают объекты ранжирования (например, критерии) в
порядке убывания их значимости (скажем, для альтернатив - это убывание
предпочтительности). Ранги обозначаются цифрами от 1 до n, где n – количество
рангов. Сумма рангов Sn при этом будет равна следующей сумме натуральных чисел:
Sn
= n(n+1)/2.
Следует иметь в виду, что ранги,
присвоенные объектам, не являются числовой мерой изучаемого качества. Ранги
представляют собой только символы, указывающие предпочтения одного объекта
перед другим. Поэтому к математическим операциям с ними надо подходить с
большой осторожностью. Некоторые специалисты считают задачу количественной
оценки качественного признака некорректной и полагают, что измерение
качественного признака возможно только в номинальной или порядковой шкале.
Однако на практике количественные оценки качественных признаков широко и
достаточно успешно применяются. Они используются для оценки предпочтительности
альтернатив при подготовке решений, для оценки важности позиций плана, при
решении задачи оптимального распределения по этим позициям ограниченных
ресурсов и т.д.
ЧТО ТАКОЕ «ШКАЛА СААТИ»?
В литературе рассматриваются различные
шкалы для измерения степени превосходства f
одного объекта над другим, например шкала Т. Саати, представленная в таблице 1.
Таблица 1.
|
f |
Определение |
Пояснение |
|
1 |
Объекты одинаково важные. |
Оба объекта вносят одинаковый вклад в
достижение цели. |
|
3 |
Слабое превосходство. |
Эксперт отдает некоторое предпочтение
первому объекту пары. |
|
5 |
Сильное превосходство. |
Эксперт определенно считает первый
объект более значимым, чем второй. |
|
7 |
Явное превосходство. |
Первый объект явно предпочтительней
второго, и опыт это подтверждает. |
|
9 |
Абсолютное превосходство. |
Превосходство первого объекта не
вызывает никаких сомнений. |
|
2, 4, 6, 8 |
Значения, соответствующие
промежуточным суждениям. |
Для случаев, когда выбор между
соседними значениями основной шкалы вызывает затруднения. |
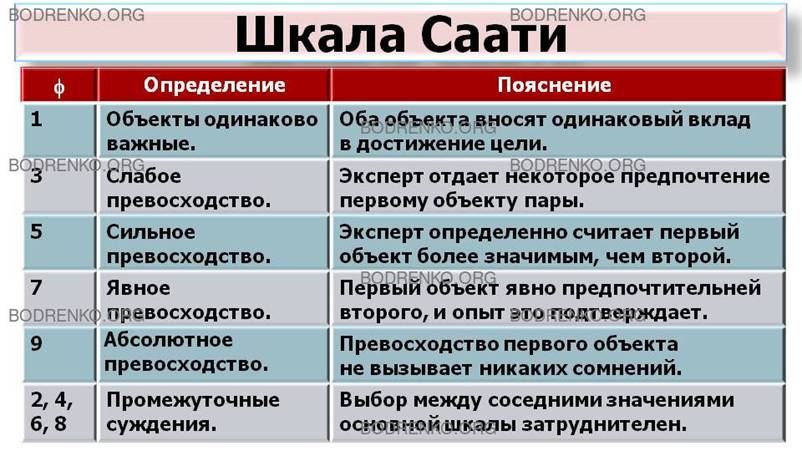
Рисунок
1.
Шкала Т. Саати степени превосходства одного объекта над другим.
Порядковая шкала, получаемая в
результате ранжирования, должна удовлетворять условию равенства числа рангов N
числу ранжируемых объектов n. Однако бывает, что эксперт не в состоянии указать
порядок следования для двух или нескольких объектов или присваивает разным
объектам один и тот же ранг. В таких случаях объектам присваивают так
называемые стандартизованные ранги. Для этого общее число стандартизированных
рангов полагают равным n, а объектам, имеющим одинаковые ранги, присваивают
стандартизованный ранг, значение которого представляет собой среднее значение
суммы мест, поделенных между собой объектами с одинаковыми рангами.
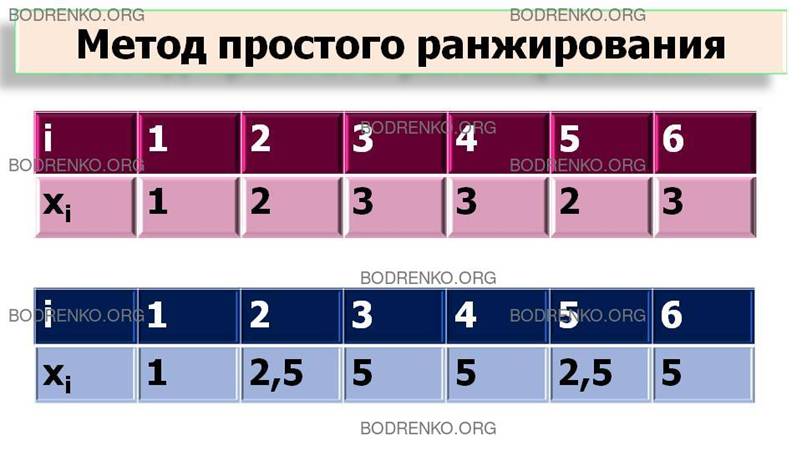
Пусть, например, шести альтернативам
присвоены следующие ранги:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
|
xi |
1 |
2 |
3 |
3 |
2 |
3 |
Тогда альтернативам 2 и 5, поделившим
между собой второе и третье места, присваивается стандартизованный ранг S = (2
+ 3)/2 = 2,5, а альтернативам 3, 4 и 6, поделившим 4, 5 и 6 места,
присваивается стандартизованный ранг S = (4+5+6)/3 = 5.
В итоге получаем следующую нормальную
ранжировку:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
|
xi |
1 |
2,5 |
5 |
5 |
2,5 |
5 |
Таким образом, сумма рангов Sn , полученная
в результате ранжирования объектов, будет равна следующей сумме натуральных
чисел:
Sn = Σ xi = n(n+1)/2,
где xi – ранг i-го объекта.
При ранжировании рационально сначала
выделить самую важную переменную, приписав ей вес 100, и наименее важную, по
возможности, также указав ее вес. Затем путем попарного сравнения присвоить
ранги всем переменным одной группы. В случае, когда ряду переменных присвоены
одинаковые ранги, следует дополнительно определить стандартизованные ранги.
Метод ранжирования редко используется в
чистом виде. Обычно его сочетают с другими методами, облегчающими различимость
альтернатив для экспертов. К примеру, сначала может быть произведена оценка
величин, а уж затем их ранжирование. Для установления более тесной связи между
оценками, приписываемыми экспертами отдельным объектам, их зачастую нормируют.
Нормирование любой меры означает, что представляющее ее число для всего
множества в целом принимается равным единице. Для нормирования каждой
конкретной оценки сначала суммируются оценки по всем объектам, а затем каждая
из них делится на полученную сумму. Когда в экспертизе участвуют несколько
экспертов, обычно стремятся получить усредненную оценку (вес) для каждого
объекта. Для этого нормированные оценки каждого объекта суммируются, а затем
полученная сумма делится на число экспертов.
В ЧЕМ ЗАКЛЮЧАЕТСЯ МЕТОД
НЕПОСРЕДСТВЕННОЙ ОЦЕНКИ?
Метод непосредственной оценки
заключается в отнесении объекта оценки к определенному значению по оценочной
шкале. То есть в присвоении объекту оценки определенного количества баллов в
определенном интервале, например, от 0 до 10 – в соответствии с предпочтением
по какому-либо признаку или их группе (альтернативы, например, оцениваются по
предпочтению; критерии – по значимости; факторы внешней среды – по оказываемому
влиянию; проблемы – по приоритетности решения).
В ЧЕМ ЗАКЛЮЧАЕТСЯ СУЩНОСТЬ МЕТОДА ПАРНЫХ
СРАВНЕНИЙ?
Метод парных сравнений. Точность и
надежность процедуры ранжирования сильно зависит от количества объектов
ранжирования. Чем меньше таких объектов, тем легче эксперту их различать.
Поэтому количество ранжируемых объектов не должно быть больше 20, а желательно,
чтобы их было меньше 10. При малом числе объектов возможно их непосредственное
ранжирование, а при числе объектов 7 ± 2 эксперт может иметь заметные трудности
в выборе наилучшего объекта. Дело в том, что человек в состоянии выбрать
наилучший объект, не прибегая к парным сравнениям только когда число объектов
не больше емкости его кратковременной памяти, которая не превышает 9 единиц
информации. Иначе результат непосредственного ранжирования становится
ненадежным.
При большом числе объектов интуитивные
оценки экспертов становятся ненадежными, и приходится прибегать к
формализованным процедурам экспертного оценивания. В этом случае эксперт должен
представить для дальнейшей обработки результаты проведенных им парных сравнений
объектов. В зависимости от типа решаемой задачи эксперт должен либо определить
более предпочтительный объект каждой рассматриваемой пары (или признать объекты
пары равноценными по рассматриваемому признаку), либо указать, во сколько раз
один из объектов предпочтительнее другого. Полученная таким образом исходная
информация обрабатывается формальными логически обоснованными методами.
Сравнивая два объекта, эксперт может определить более предпочтительный из них,
либо признать эти объекты эквивалентными. В методе парных сравнений от эксперта
не требуется последовательности в суждениях, т.е. предпочтения эксперта не
обязательно должны быть транзитивными. Это условие особенно существенно при
большом числе оцениваемых объектов, когда эксперту даже при желании трудно
запомнить высказанные им ранее суждения о предпочтениях. Нетранзитивность
экспертных предпочтений отнюдь не является редким событием Установлено, что
число таких суждений велико и может достигать 30% от их общего количества,
особенно при сравнении нечетких множеств. Основная причина этого явления
заключается в способе мышления человека, который обычно стремится заменить
сложную проблему последовательностью более простых задач. Выбор по сложному
качественному признаку также может быть представлен как выбор по совокупности
нескольких более простых признаков. А далее может происходить следующее:
эксперт, сравнивая одну пару объектов, принимает за решающий один частный
признак, а сравнивая другую пару объектов, может посчитать более важным другой
частный признак. Это и приводит к противоречивости его суждений.
ЧТО ТАКОЕ МАТРИЦА ПАРНЫХ СРАВНЕНИЙ?
При использовании метода парных
сравнений составляется матрица парных сравнений. Метод парных сравнений заключается в определении предпочтений
элементов, расположенных в левом столбце, над элементами, расположенными в верхней
строке составляемой таблицы (матрицы парных сравнений). При использовании
данного метода составляется матрица, по строкам и столбцам которой располагают сравниваемые
объекты. В этом методе ранги объектов подсчитывают после составления матрицы. Рассмотрим
пример составления матрицы парных сравнений для четырех объектов A1, A2, A3, A4 (таблица 2)
и вычислим их ранги.
Таблица 2.
|
|
A1 |
A2 |
A3 |
A4 |
Ранг |
|
A1 |
--- |
1 (A1,2) |
0 (A1,3) |
1 (A1,4) |
2 |
|
A2 |
0 (A2,1) |
--- |
0 (A2,3) |
1 (A2,4) |
1 |
|
A3 |
1 (A3,1) |
1 (A3,2) |
--- |
1 (A3,4) |
3 |
|
A4 |
0 (A4,1) |
0 (A4,2) |
0 (A4,3) |
--- |
0 |

Рисунок
2.
Пример матрицы парных сравнений.
Пусть, например, элемент A1 получает
большую оценку, чем элемент A2.
Тогда в ячейку (A1,2)
вписываем единицу. Соответственно в ячейку (A2,1) вписываем ноль.
Пусть, например, элемент A1 получает
меньшую оценку, чем элемент A3.
Тогда в ячейку (A1,3) вписываем ноль. Так как при этом элемент
А3 получает большую оценку, чем элемент A2, то соответственно в ячейке (А3,1) пишем единицу.
Пусть, например, элемент A1 получает
большую оценку, чем элемент A4.
Тогда в ячейку (A1,4) вписываем единицу. Так как при этом
элемент A4
получает меньшую оценку, чем элемент A1, то соответственно
в ячейке (A4,1)
пишем ноль.
Далее, пусть, например, элемент A2 получает
меньшую оценку, чем элемент A3.
Тогда в ячейку (A2,3) вписываем ноль. Так как при этом элемент
А3 получает большую оценку, чем элемент A2, то соответственно в ячейке (А3,2) пишем единицу.
Пусть, например, элемент A2 получает
большую оценку, чем элемент A4.
Тогда в ячейку (A2,4) вписываем единицу. Так как при
этом элемент A4
получает меньшую оценку, чем элемент A2, то соответственно
в ячейке (A4,2)
пишем ноль.
Далее, пусть, например, элемент A3 получает
большую оценку, чем элемент A4.
Тогда в ячейку (А3,4) вписываем единицу 1, соответственно в ячейку (A4,3) вписываем
ноль.
Для получения рангов объектов суммируем
полученные значения по строкам. В данном примере получаем следующие ранги: ранг
A1
= 2, ранг A2
= 1, ранг A3
= 3, ранг A4
= 0.
В ЧЕМ ЗАКЛЮЧАЮТСЯ ПРЕДПОСЫЛКИ
ПРИМЕНЕНИЯ МЕТОДА ПОСЛЕДОВАТЕЛЬНЫХ ПРЕДПОЧТЕНИЙ?
Общим дефектом показателей, получаемых
на основе суммирования баллов, является то, что недостаток качества по одному
из них можно компенсировать за счет другого, получая один и тот же результат
при различной значимости факторов. Поэтому для повышения надежности подобных
оценок важно выявление связей и установление зависимостей между всеми значимыми
факторами. Суммирование баллов, расчет результирующих рангов и оценок должны
быть основаны не только на их упорядочении, но и еще на некоторых логических
допущениях о зависимостях, используя которые можно более или менее обоснованно
приписывать качественно разным факторам веса в одинаковых единицах по общей
шкале измерения.
Перечислим основные логические допущения,
применяемые в методе последовательных предпочтений.
1. Каждому результату (событию,
фактору) соответствует действительное неотрицательное число vj ,
рассматриваемое как оценка истинной значимости Oj;
2.
Если результат Oj более важен, чем результат Ok , то vj > vk , и если
Oj равноценен Ok , то vj = vk ;
3. Если оценки vj и vk соответствуют
результатам Oj и Ok , то оценка vj + vk соответствует общему результату Oj + Ok.
Это допущение выполняется, когда результаты дискретны, непротиворечивы и
взаимно независимы.
В ЧЕМ СОСТОИТ ПРОЦЕДУРА
ПОСЛЕДОВАТЕЛЬНЫХ СРАВНЕНИЙ?
Процедура последовательных сравнений
состоит в следующем.
Эксперту предоставляется перечень
факторов (критериев, альтернатив, результатов), которые необходимо оценить по
их относительной важности (значимости), и он производит их ранжирование.
Наиболее важному фактору придается вес (v1), равный единице, а остальным
факторам оценки между единицей и нулем в порядке их относительной важности.
Затем эксперт устанавливает, является ли фактор с оценкой 1 более важным, чем
комбинация остальных факторов. Если это так, то он увеличивает оценку v1 (если
это необходимо), чтобы она была больше суммы всех остальных факторов. Если нет,
то он корректирует оценку v1 (если это необходимо) так, чтобы она была меньше
суммы всех остальных факторов.
Далее определяется, является ли второй
по важности фактор с оценкой v2 более важным, чем все остальные факторы,
получившие более низкие оценки; повторяется та же процедура, что и для v1 .
Процедура последовательных сравнений
продолжается вплоть до (n–1)-го фактора.
НА КАКОМ ПРЕДПОЛОЖЕНИИ ОСНОВАНО ПРИМЕНЕНИЕ
МЕТОДА ПОСЛЕДОВАТЕЛЬНЫХ ПРЕДПОЧТЕНИЙ?
Применение метода последовательных предпочтений
основано на предположении о том, что если задан некоторый интервал
действительного переменного, скажем от 0 до 1, то эксперт, основываясь на
имеющейся у него информации, может установить предварительные оценки для
каждого события, а затем уточнить их на основе сравнения с помощью определенной
логической процедуры. Поскольку множества, содержащие 7 и более элементов,
трудно упорядочить этим методом, целесообразно разбивать их на подмножества с
числом элементов до шести. Трудности использования ранжирования,
непосредственной оценки и метода последовательных сравнений при выявлении
предпочтений для большого числа объектов (факторов, альтернатив) можно в определенной степени уменьшить, если
воспользоваться методом парных сравнений, который позволяет установить в каждой
паре наиболее важный (значимый) элемент.
ПРИМЕР ПРИМЕНЕНИЯ МЕТОДА
ПОСЛЕДОВАТЕЛЬНЫХ ПРЕДПОЧТЕНИЙ.
Порядок действий следующий.
Шаг 1. Упорядочить результаты в
соответствии с их значимостью (относительной важностью) с точки зрения
эксперта. Пусть О1 представляет наиболее важный результат, О2 – следующий по
степени важности и т.д., а Оm – наименее важный.
Шаг 2. Приписать вес 1,00 результату О1
(т.е. v1 =1,00) и другие веса – всем остальным результатам.
Шаг 3. Сравнить О1 с О2 + О3 +... + Оm,
при этом:
а) если О1 предпочтительнее О2 + О3
+... + Оm , изменить (в случае необходимости) значение v1 так, чтобы
выполнялось неравенство v1 > v2 + v3 + ... + vm . При этой корректировке,
так же как и при всех остальных, следует стремиться к тому, чтобы веса набора
(v2 , v3 и т.д.) остались без изменений. Далее следует перейти к шагу 4;
б) если О1 и О2 + О3 +... + Оm
равноценны, то изменить (в случае необходимости) значение v 1 так, чтобы
выполнялось равенство v 1 = v 2 + v 3 +... + v m , и затем перейти к шагу 4;
в) если результат О1 менее
предпочтителен, чем О2 + О3 +... + Оm , то изменить (в случае необходимости)
значение v1 так, чтобы выполнялось неравенство v1 < v2 + v3 +... + vm .
Далее сравнить О1 с О2 + О3 +... + О m-1 и повторять описанную процедуру до тех
пор, пока О1 будет или предпочтительнее, или равноценен всем остальным
результатам.
Шаг 4. Сравнить О2 с О3 + О4 +... + Оm
и выполнить весь шаг 3.
Шаг 5. Продолжить шаг 4 до тех пор,
пока не будет выполнено сравнение Оm-2 с Оm-1 + Оm.
Шаг 6. Преобразовать каждое полученное
значение vj в нормированное v’j. Для
этого соответствующие веса делят на
сумму всех vj . В итоге сумма всех значений v’j должна быть равна 1,00.
ПРИМЕР.
Пусть возможны четыре альтернативы,
которые необходимо «взвесить» по их значимости. Пусть О1 считается наиболее
важной из них, О2 – следующая, далее идут О3 и О4 .
Допустим, что эксперт приписал
результатам О1, О2, О3 и О4 веса 1,00; 0,80; 0,50 и 0,30 соответственно.
Обозначим эти величины символами v1 , v2 , v3 и v4 и будем рассматривать их как
первые оценки «истинных» значений О1, О2 , О3 и О4.
Мы имеем: v1 = 1,00; v2 = 0,80; v3 =
0,50; v4 = 0,30.
Кроме того предположим, что эксперт
утверждает, что О1 предпочтительнее суммы остальных альтернатив. Кроме того,
эксперт утверждает, что О3 + О4 предпочтительнее, чем О2 .
Заметим, что v2 + v3 + v4 = 0,80 + 0,50 + 0,30 = 1,60.
Поскольку эксперт утверждает, что О1
предпочтительнее суммы остальных альтернатив, следует изменить оценку v1 так,
чтобы выполнялось неравенство v1 > v2 + v3 + v4 . Например, можно принять,
что v1 = 2,00. При этом значения оценок v2 , v3
и v4 оставим без изменений (v2 = 0,80; v3 = 0,50; v4 = 0,30).
Заметим, что v3 + v4 = 0,50 + 0,30 = 0,80.
Далее, поскольку эксперт считает, что
О3 + О4 предпочтительнее, чем О2 , требуется дальнейшее изменение
первоначальных оценок.
Например, можно принять v1 = 2,00; v2 = 0,70; v3 = 0,50; v4 = 0,30. Если эти
оценки не противоречат мнениям экспертов, можно их нормировать, разделив каждую
из них на сумму всех оценок, которая в данном случае равна 3,50.
Обозначив нормированные оценки
символами v’j, получим:
v’1 = 2,00/3,50 = 0,57;
v’2 = 0,70/3,50 = 0,20;
v’ 3 = 0,50/3,50 = 0,14;
v’4 = 0.30/3,50 = 0,09.
Для
нормированных оценок имеем: v’1+
v’2 + v’3 + v’4 = 0,57 + 0,20 + 0,14 + 0,09 = 1,00.

КАКОВЫ ОСНОВНЫЕ РАЗНОВИДНОСТИ ЭКСПЕРТНЫХ
ОПРОСОВ?
Метод экспертных оценок предполагает
ряд процедур, направленных на получение необходимого и достаточного набора
суждений специалистов, их интеграции в общий практический вывод. Различают
очные и заочные (как правило, анонимные) опросы, а также одноразовые и
многоразовые (в несколько туров) опросы.
Основными разновидностями очного опроса
являются «мозговая атака», которая достаточно подробно была описана на лекции 1
«Основы методологии принятия управленческих решений», «метод комиссии» и «метод
отнесенной оценки».
Основные заочные техники – разовый
анонимный опрос и метод Дельфи.
В ЧЕМ СОСТОИТ СУЩНОСТЬ МЕТОДА ДЕЛЬФИ?
Одним из широко распространенных
методов групповой оценки является метод Дельфи (Дельфы – греческий город,
мудрецы которого славились предсказаниями будущего). Этот метод был разработан для составления всевозможных прогнозов. В
основу метода положена идея о потенциальной возможности самообучения экспертов
при проведении заочного опроса в несколько туров. Гарантируется соблюдение
анонимности респондентов (во избежание «давления авторитетов» и опасения
«потерять лицо» при неудачном ответе). Респондентам предоставляется возможность
знакомиться с материалами предыдущего тура и последовательно уточнять свои
оценки по мере изучения новых аргументов.
КАКОВЫ ОСНОВНЫЕ ПРЕДПОСЫЛКИ ПРИМЕНЕНИЯ
МЕТОДА ДЕЛЬФИ?
Основные предпосылки применения метода
Дельфи:
1) поставленные вопросы должны
допускать возможность выражения ответа в виде числа;
2) эксперты должны располагать
достаточной информацией для того, чтобы дать оценку;
3) ответ на каждый из вопросов (оценка)
должен быть обоснован экспертом.
Технология проведения экспертизы
методом Дельфи помогает экспертам избавиться от сковывающих факторов (мнения
руководителей, господствующих взглядов большинства, эмоционального воздействия
оппонентов, затруднительности публичного отказа от ранее высказанного мнения и
т.п.). Вместе с тем сохраняется ценная возможность не только высказывать
оригинальные суждения, но и менять их с учетом новой информации без риска для
своей репутации.
КАКОВЫ ОСНОВНЫЕ ЧЕРТЫ ПРОЦЕДУР,
ПРИМЕНЯЕМЫХ В МЕТОДЕ ДЕЛЬФИ?
Процедуры, используемые в методе
Дельфи, характеризуются тремя основными чертами: анонимностью, регулируемой
обратной связью и групповым ответом.
Эксперты заполняют анонимные анкеты или
подключаются к компьютерной сети, что повышает скорость опроса при сохранении
анонимности. Анонимность опроса позволяет уменьшить влияние отдельных
доминирующих экспертов.
Регулируемая обратная связь
обеспечивается за счет проведения нескольких туров опроса, причем результаты
каждого тура обрабатываются с помощью статистических методов и сообщаются
экспертам. Статистическая обработка осуществляется так, чтобы уменьшить разброс
индивидуальных оценок и получить групповой ответ, в котором правильно отражено
мнение каждого эксперта. Регулируемая обратная связь позволяет уменьшить
случайные отклонения, вызванные влиянием индивидуальных и групповых интересов,
не связанных с решаемой проблемой. Введение обратной связи вносит элемент
объективности и делает оценки более надежными.
Проведение опросов в несколько туров, в
течение которых осуществляется ряд последовательных итераций (экспертов
информируют о результатах предыдущих этапов опроса и предлагают в ряде случаев
обосновать свое мнение), позволяет уменьшить колебания в индивидуальных
ответах, ограничивает внутригрупповые колебания. Это не значит, конечно, что
частные заключения меньшинства или одиночек не должны приниматься во внимание.
Напротив, их стоит исследовать особенно тщательным образом. Но для рекомендаций
в сфере планирования и управления, прежде всего, важны максимально надежные оценки. В этом
отношении согласованное мнение большой группы первоклассных экспертов имеет
важное значение.
В
ЧЕМ СОСТОИТ ЦЕЛЬ МЕТОДА ДЕЛЬФИ?
Цель метода Дельфи заключается в том,
чтобы получить согласованную информацию высокой степени достоверности от группы
экспертов. Метод разработан сотрудниками американской фирмы Rand Corporation в
1964 году. В нем реализована попытка устранить противоречие, возникающее при организации
работы группы экспертов. Суть его заключается в том, что если опрашивать
экспертов независимо друг от друга, то возможны отклонения в больших пределах.
А если позволить экспертам взаимодействовать, обмениваться мнениями в процессе
работы, то это может привести к появлению оценок, навязанных авторитетными
коллегами. Поэтому при применении метода Дельфи осуществляется процедура, обеспечивающая
обмен информацией о доводах и ответах, без непосредственного взаимодействия
экспертов друг с другом. Прямые дискуссии экспертов заменяются индивидуальными
опросами, проходящими по определенной программе в несколько этапов (рисунок 3).
Первый этап. Формирование рабочей
группы.
Второй этап. Выбор экспертов.
Третий этап. Составление анкеты (опросного
листа).
Четвертый этап. Опрос экспертов.
На четвертом этапе (опрос экспертов)
происходит:
- уточнение объекта опроса и получение
мнений экспертов;
- вероятностная оценка рабочей модели;
- согласование оценок экспертов.
Пятый этап. Обобщение экспертных
заключений и подготовка рекомендаций по исследуемой проблеме.
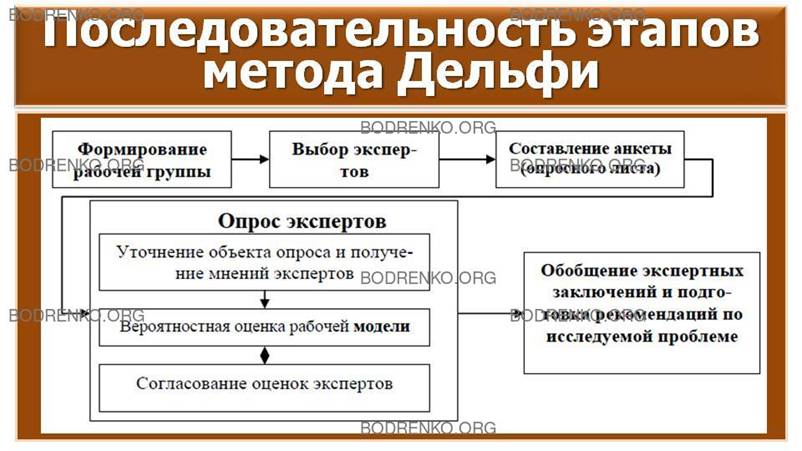
Рисунок
3. Последовательность этапов метода Дельфи.
Этапы опроса повторяют столько раз,
сколько необходимо для достижения согласованного решения.
КАК ПРОВОДИТСЯ ОПРОС ЭКСПЕРТОВ ПО
МЕТОДУ ДЕЛЬФИ?
Обычно опрос проводится в четыре тура,
если, конечно, эксперты не пришли к согласию ранее. Во время каждого тура
эксперт должен выразить свое мнение в виде числа на заранее подготовленной
шкале оценок. Аналитики обрабатывают полученные оценки и рассчитывают медиану и
квартили.
После первого тура каждому эксперту
сообщается значение медианы и размах между крайними квартилями. По существу
после первого тура эксперты знакомятся с итоговыми характеристиками позиции
группы в целом. Экспертов, чьи оценки оказались в крайних квартилях, просят
обосновать причины расхождения с групповым мнением. Эксперты могут приводить
любые аргументы и возражения, как и во время любой дискуссии. Они могут
пересмотреть свои мнения и при желании исправить оценки. С полученными
обоснованиями знакомят остальных экспертов, не указывая при этом, чьи они.
Такая процедура позволяет всем экспертам принять в расчет обстоятельства,
которые они могли случайно пропустить или которыми пренебрегли во время первого
тура опроса.
Во втором туре эксперты получают
возможность либо сблизить свое мнение с позицией большинства, либо изучить и
обсудить причину отклонения. В последующих турах участников просят учесть
возражения и прокомментировать их.
Практика показывает, что типичным для
первого тура опроса является широкий разброс индивидуальных ответов. По мере
применения итерации и обратной связи сходимость индивидуальных ответов
увеличивается. Эксперименты позволяют предполагать, что при использовании
метода Дельфи наличие в группе менее компетентных экспертов оказывает меньшее
влияние на групповую оценку, чем при простом усреднении оценок, поскольку
итерация помогает этим экспертам улучшить свои оценки за счет информации,
получаемой от более компетентных специалистов. С другой стороны, компетентные
специалисты все же не располагают той полнотой информации, которая имеется у
всех входящих в группу экспертов, что позволяет и им улучшать свои оценки в
процессе опроса.
В КАКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПРОИСХОДИТ
РАЗРАБОТКА ЭКСПЕРТНОГО РЕШЕНИЯ ПО МЕТОДУ ДЕЛЬФИ?
Разработка экспертного решения по
методу Дельфи осуществляется в следующей последовательности:
1) членам группы предлагается ответить
на детально сформулированный перечень вопросов по рассматриваемой проблеме;
2) каждый участник отвечает на вопросы
независимо и анонимно;
3) результаты ответов собираются в
центре, и на их основании составляется интегральный документ, содержащий все
предлагаемые варианты решений;
4) каждый член группы получает копию
этого материала;
5) ознакомление с предложениями других
участников может изменить мнение по поводу возможных вариантов решения;
6) предыдущие два шага повторяются
столько раз, сколько необходимо для достижения согласованного решения.
КАКОВЫ УСЛОВИЯ ПРИМЕНЕНИЯ МЕТОДА
ДЕЛЬФИ?
Метод Дельфи применим,
когда нет ограничений по времени выработки решения и согласованные решения
принимаются самими экспертами. Метод Дельфи часто используют в
случаях, когда сбор группы невозможен. Более того, в соответствии с методикой
членам группы не разрешается встречаться и обмениваться мнениями по поводу
решаемой проблемы, обеспечивается независимость мнений. Однако затраты времени
на разработку решений существенно растут.
К недостаткам метода Дельфи следует
отнести значительные затраты времени на процедуру экспертизы, а также
невозможность прямого столкновения мнений экспертов, что не всегда стимулирует
генерирование идей, возникающее при личных контактах специалистов.
РАЗДЕЛ 2. ОТБОР ЭКСПЕРТОВ И ОРГАНИЗАЦИЯ
ИХ РАБОТЫ.
ИСПОЛЬЗОВАНИЕ ЭКСПЕРТНЫХ ОЦЕНОК.
Индивидуальные качества эксперта
зависят от его знаний, опыта, интеллекта, способности предвидеть будущее и ряда
других факторов, измерить которые сложно или вообще невозможно. Факторы,
влияющие на способность индивидуума выдавать полезную информацию в условиях
неопределенности, разделяют, на
внутренние (индивидуальные) и внешние (социальные).
Внутренние факторы могут привести к
отклонениям в оценках, даваемых экспертом. Эти отклонения могут быть как
ненамеренными, т.е. связанными с излишне оптимистическим или пессимистическим
отношением эксперта к рассматриваемой проблеме, так и намеренными, зависящими
от индивидуальной установки эксперта.
Внешние факторы включают те влияния на
оценки эксперта, которые в большей степени зависят не от его личности, а от его
взаимодействия с окружающей средой (коллективом, обществом). Эти влияния могут
быть вызваны целями организации, в которой работает эксперт, его положением в
структуре этой организации, степенью ответственности за результаты экспертизы и
т.п. Применение формализованных процедур получения экспертных оценок, их
обработка с помощью методов теории вероятностей и математической статистики
позволяет в определенной мере скомпенсировать смещение индивидуальных оценок,
уточнить структуру решаемой проблемы и снизить уровень ее неопределенности по
сравнению с исходным состоянием.
Основные ограничения, возникающие при
использовании экспертов в качестве источников информации и ведущие к
возникновению погрешностей, можно свести в пять групп:
1) уровень доступной информации;
2) несовершенство информации;
3) двусмысленность вопросов;
4) несовершенство модели;
5) прочие погрешности.
Когда вся доступная информация о
вероятностном событии использована, остающаяся неопределенность может быть
описана с помощью распределения вероятностей возможных исходов. Никакие
дальнейшие опросы специалистов или другой анализ имеющейся информации не снизят
неопределенность ниже этого уровня. Снижение уровня неопределенности может быть
достигнуто лишь при получении новой информации. Помимо погрешностей,
возникающих вследствие недостатка информации, большое влияние на результаты
экспертизы оказывают смещения, вносимые самой процедурой сбора и анализа мнений
экспертов.
КАКОВЫ ОСНОВНЫЕ ЭТАПЫ ПРОВЕДЕНИЯ
ЭКСПЕРТИЗЫ?
Основные этапы проведения экспертизы,
последовательность и содержание которых может меняться в зависимости от
реальных условий и ограничений, включают:
1) четкое и однозначное формулирование
цели экспертизы и разработку процедуры опроса;
2) формирование группы
специалистов-аналитиков;
3) проведение опроса;
4) анализ и обработку информации,
полученной от экспертов;
5) синтез объективной (статистической)
информации, полученной в результате экспертизы, с целью приведения ее в форму,
удобную для принятия решения.
Разработать методы отбора экспертов,
гарантирующих полную достоверность получаемой от них информации, практически
невозможно. Задача заключается в обеспечении процедуры отбора экспертов,
минимизирующей искажения информации, возникающие вследствие некомпетентности
отобранных специалистов или их нежелания давать достоверную и надежную информацию.
Целый ряд таких процедур описан в научной литературе.
Следует обратить внимание также на
необходимость выявления потенциально возможных целей экспертов, противоречащих
целям экспертизы. Нужно выяснить наличие причин, которые могут вызвать сознательное
смещение групповой оценки в направлении, желательном для данного эксперта или
группы экспертов. Рекомендуется исключать из рассмотрения те события, в
результатах которых эксперты лично заинтересованы, либо заменить саму группу
экспертов.
КАКОВЫ ОБЯЗАТЕЛЬНЫЕ УСЛОВИЯ ВЫБОРА
ЭКСПЕРТОВ?
При выборе экспертов должны быть
поставлены следующие обязательные условия.
1) УСЛОВИЕ ПОЛНОТЫ СИСТЕМЫ ПРЕДПОЧТЕНИЙ
ЭКСПЕРТОВ: эксперты должны быть в состоянии для всех объектов множества A
(a, b, c , ..., m Î
A) указать для каждой пары объектов свои предпочтения (a << b или a >>
b). Эксперт должен быть компетентным в
тех вопросах, которые выносятся на экспертизу;
2) УСЛОВИЕ ТРАНЗИТИВНОСТИ СИСТЕМЫ
ПРЕДПОЧТЕНИЙ ЭКСПЕРТОВ. Это условие соблюдается, если для трех любых
компетенций a , b , c из a >> b и b >> c следует a >> c;
3) Эксперт не должен являться лицом,
принимающим решение на основе полученной информации. Он может быть только
советником того, кто берет на себя ответственность за постановку цели, план, программу
или проект. В противном случае возникает соблазн «подчинения» экспертизы
заранее запланированному решению, прикрытия воли руководителя ссылкой на
«мнение экспертов»;
4) Необходимым является также
оптимальное сочетание узкой специализации и общего кругозора эксперта, а также
оптимальное сочетание его индивидуальных качеств.
5) Еще одним весьма важным критерием
отбора является наличие у эксперта высоких моральных качеств. Ясно, что это
очень трудно оценить, однако очевидно, что без должного морального уровня эксперта
остальные его качества могут оказаться бесполезными, способными лишь увеличить
опасность получения псевдопрогноза.
КАКОВЫ ОСНОВНЫЕ МЕТОДЫ ОТБОРА
ЭКСПЕРТОВ?
Методы отбора экспертов сводятся к двум
основным подходам: объективному и субъективному.
В ЧЕМ СОСТОИТ ОБЪЕКТИВНЫЙ ПОДХОД В ОТБОРЕ
ЭКСПЕРТОВ?
Объективный подход имеет, в свою очередь, два варианта – документальный и экспериментальный.
Документальный метод
предусматривает подбор экспертов на основе анкетных и социально-демографических
данных.
Экспериментальный метод проводится
на основе испытания, тестирования кандидата в эксперты, либо по результатам эффективности
его прежней экспертной деятельности.
Оба методических приема требуют большой
деликатности по отношению к будущему эксперту. Так, тестирование не всегда приемлемо
с этической точки зрения. Кроме того, валидность и надежность тестов нередко
вызывает сомнения.
В ЧЕМ СОСТОИТ СУБЪЕКТИВНЫЙ ПОДХОД В ОТБОРЕ
ЭКСПЕРТОВ?
Субъективный подход при отборе экспертов
также распадается на несколько приемов.
Один из них – аттестация, когда подбор экспертов осуществляется с помощью
открытого или тайного голосования потенциальных членов будущей экспертной
группы с отводом тех из них, кто не набрал определенного минимума голосов.
Здесь могут использоваться методики с расширяющимися кругами экспертов в
несколько туров. В первом туре круг экспертов составляет списки кандидатов в
эксперты. Туры повторяются до тех пор, пока состав кандидатов в эксперты не стабилизируется.
Затем проводится расчет коэффициентов компетентности экспертов в зависимости от
числа включений в списки.
Сам по себе этот прием достаточно
эффективен, но лишь при условии, что члены будущей группы хорошо знают друг
друга и обладают высокой добросовестностью. В противном случае возникает
опасность отвода по случайным, непринципиальным мотивам.
Другой прием – метод взаимной оценки будущих экспертов (в баллах или
ранжированием) – является по существу разновидностью первого со всеми его
особенностями и ограничениями.
Третий прием – метод самооценки степени компетентности и объективности. Здесь,
правда, имеется опасность завышенных самооценок. Но практика показывает, что
серьезные эксперты, напротив, склонны несколько занижать свои оценки и
стремятся не принимать участие в экспертизах, выходящих за рамки их интересов.
На практике часто применяется способ,
когда каждый эксперт оценивает компетентность всех членов экспертной группы, в
том числе и свою собственную, используя заранее установленную балльную шкалу.
Например, в таблице 3 используются следующие числовые значения: 1 – слабая
компетентность в рассматриваемой области, 2 – удовлетворительная
компетентность, 3 – хорошая компетентность, 4 – высокая компетентность в этой
области.
Таблица 3.
|
Ф.И.О. эксперта |
№ эксперта |
слабая компетентность |
удовлетворительная компетентность |
хорошая компетентность |
высокая компетентность |
|
|
1 |
|
|
+ |
|
|
|
2 |
|
+ |
|
|
|
|
3 |
|
|
|
+ |

Рисунок
4. Балльная шкала компетентности экспертов в рассматриваемой области.
Вместе с тем, очевидно, что ни один из
перечисленных методов и приемов отбора экспертов не является универсальным и
что методика отбора должна базироваться на сочетании различных приемов.
КАК МОЖЕТ БЫТЬ ОРГАНИЗОВАНА РАБОТА
ЭКСПЕРТОВ?
На практике численность экспертной
группы большей частью составляет примерно 5 – 7, максимально 10 – 15 человек
при очных опросах и 20 – 30, максимально 60 – 80 человек при заочных опросах, в
зависимости от характера экспертизы. За этими пределами увеличение числа
экспертов не дает существенного прироста новой информации ни в деталях, ни,
главное, по качеству. Кроме того, требуется разумное сочетание экспертов
различного возраста, темперамента, различного служебного положения, производственного
и жизненного опыта. Известно, что члены экспертной группы не любят начинать работу
с «чистого листа». Набор конкретных вопросов, а в ряде случаев и вероятных
ответов помогает эксперту лучше понять поставленную задачу.
Поэтому в большинстве экспертных
методов экспертам предлагают анкету, которая обычно содержит три группы вопросов:
1) объективные данные о самом эксперте
(возраст, образование, профессия, стаж работы, ученое звание, узкая
специализация и т.п.);
2) характеристики, позволяющие оценить
мотивы, которыми руководствуется эксперт при оценке исследуемой проблемы;
3) основные вопросы, касающиеся
существа исследуемой проблемы.
КАКИЕ ФОРМЫ ВОПРОСОВ ПРЕДЛАГАЮТСЯ
ЭКСПЕРТАМ?
По форме вопросы могут быть ОТКРЫТЫМИ,
ЗАКРЫТЫМИ, ПРЯМЫМИ И КОСВЕННЫМИ.
КАКОЙ ВОПРОС НАЗЫВАЕТСЯ ОТКРЫТЫМ?
Вопрос называется открытым или свободным, если ответ на него может быть дан в любой
форме.
КАКОЙ ВОПРОС НАЗЫВАЕТСЯ ЗАКРЫТЫМ?
Вопрос называется закрытым, если в его формулировке содержатся варианты возможных
ответов (перечень альтернатив) и эксперт должен остановить свой выбор на одном
или нескольких из них. Одной из разновидностей закрытого вопроса является
дихотомический вопрос, в котором возможна только альтернатива «да – нет».
В ЧЕМ СОСТОЯТ ОСНОВНЫЕ ПРЕИМУЩЕСТВА И
НЕДОСТАТКИ ОТКРЫТЫХ ВОПРОСОВ?
Основным преимуществом открытых
вопросов является то, что с их помощью можно обнаружить новый, совершенно
неожиданный для аналитиков аспект проблемы. Основными недостатками являются возможная
несопоставимость данных опроса и сложность анализа.
В ЧЕМ СОСТОЯТ ОСНОВНЫЕ ПРЕИМУЩЕСТВА И
НЕДОСТАТКИ ЗАКРЫТЫХ ВОПРОСОВ?
Преимущество закрытых вопросов состоит
в том, что они строго и однозначно интерпретируются и требуют меньше времени на
обработку. Вместе с тем анкета с закрытыми вопросами таит в себе опасность
навязывания эксперту ответов, особенно в тех случаях, когда по тому или иному
вопросу он вообще не имеет своего сложившегося мнения или же когда его мнение
не совпадает с ответами анкеты.
КОГДА ПРИМЕНЯЮТСЯ КОСВЕННЫЕ ВОПРОСЫ?
Цели опросной анкеты могут быть
замаскированными, и тогда признаки анкеты называют косвенными. Такие анкеты
применяются, когда нет уверенности в том, что эксперт по данному вопросу сумеет
(или захочет) дать определенную информацию.
При подборе вопросов анкеты необходимо
провести проверку того, чтобы они не допускали двойного толкования. С этой целью
полезно «проиграть» анкету самим аналитикам. Если распределение суждений по
некоторому вопросу обладает значительным стандартным отклонением, то можно
предположить, что этот вопрос двусмыслен.
РАЗДЕЛ 3. АНАЛИЗ СОГЛАСОВАННОСТИ
ЭКСПЕРТНЫХ ОЦЕНОК.
ОСНОВЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
ИНФОРМАЦИИ, ПОЛУЧЕННОЙ ОТ ЭКСПЕРТОВ.
Групповое ранжирование объектов,
полученное на основе близких индивидуальных ранжирований, вызывает обычно
большее доверие, чем ранжирование, полученное на основе существенно
различающихся индивидуальных ранжирований. Известно, что групповая оценка может
считаться достаточно надежной только при условии хорошей согласованности
ответов опрашиваемых специалистов. Поэтому статистическая обработка информации,
полученная от экспертов, должна включать:
1) оценку степени согласованности
экспертов по каждому признаку в отдельности и по всему набору признаков в
целом;
2) выделение подгрупп экспертов с
близким мнением в случае существенных расхождений в ответах;
3) выявление причин разброса мнений,
определяющих влияние характеристик экспертов на содержание ответов, и
осуществление мероприятий, позволяющих повысить достоверность оценок экспертов.
Количественная оценка согласованности
экспертных ранжирований и выяснение причин имеющихся расхождений очень важны
для анализа результатов экспертизы. Такой анализ позволяет обнаружить ошибки
расчета, а в ряде случаев выявляет существенное различие в подходах экспертов к
оценке некоторых объектов. Экспертные оценки нельзя считать случайными
величинами, если экспертами являются компетентные (по вопросам данной
экспертизы) специалисты.
В специальной литературе
рассматривается целый ряд методов статистической обработки информации,
позволяющих решить сформулированные задачи. К наиболее распространенным методам относятся расчет коэффициентов
ассоциации, метод ранговой корреляции, расчет коэффициентов конкордации и др.
КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ
КЕНДАЛЛА.
Для оценки согласованности двух
экспертных ранжирований можно использовать коэффициент ранговой корреляции Кендалла
«тау».
Данные для анализа представлены в порядковой шкале. Мерой связи, которая соответствует шкале порядка, является коэффициент ранговой корреляции Кендалла. Коэффициент корреляции «тау» Кендалла имеет те же свойства, что и коэффициент Спирмена (изменяется от –1 до +1, для независимых случайных величин равен нулю), однако он считается более информативным. Он основан на подсчете несовпадений в порядке следования ранжировок Х и Y. Для каждой пары подсчитывается число совпадений и инверсий: совпадение, если их порядок по Х и Y одинаков; инверсия, если порядок различен. Разница числа «совпадений» и числа «инверсий», деленная на N(N–1)/2, (N – число ранжируемых признаков, черт) дает коэффициент «тау». Число совпадений обозначим через P, число инверсий – через Q. Эмпирическое значение коэффициента ранговой корреляции «тау» вычисляется по формуле:
t = 2(P – Q)/ N(N-1).

Коэффициент ранговой корреляции Кендалла «тау» принимает значения от –1 до +1. При
полном совпадении экспертных ранжирований «тау» = 1, а при строго
противоположных ранжированиях «тау» = –1.
КОЭФФИЦИЕНТ КОНКОРДАЦИИ КЕНДАЛЛА.
В качестве показателя согласованности
группового ранжирования М.Кендалл ввел коэффициент конкордации W (англ. concord – согласие), оценивающий относительную
величину суммы квадратов разности рангов. При этом рассматривается разность между суммой
рангов si,
приписываемых всеми экспертами i-му объекту, и средним значением такой суммы sср.
Коэффициент конкордации (согласованности) Кендалла используется в
случае, когда совокупность объектов характеризуется несколькими
последовательностями рангов, исследователю необходимо установить статистическую
связь между этими последовательностями. Такие задачи возникают, например, при
анализе экспертных оценок: несколько экспертов ранжируют одни и те же объекты по
определенному качеству, а для проведения углубленного анализа ситуации и
принятия обоснованного решения требуется определить степень согласованности
мнений группы экспертов.
Значения коэффициента конкордации W, в отличие от коэффициента корреляции, заключены в интервале 0 ≤ W ≤ 1 . Коэффициент конкордации равен единице при полном совпадении всех ранговых последовательностей. Если мнения экспертов (ранговые последовательности) полностью противоположны, коэффициент конкордации равен нулю (коэффициент корреляции в этом случае будет равен –1).
При решении практических задач близость
показателя согласованности экспертных ранжирований к одному из крайних значений
считаются нежелательной. Если величина показателя согласованности близка к
нулю, то это обычно свидетельствует либо о недостаточной компетентности по
крайней мере части экспертов, либо о нечеткой формулировке организаторами
экспертизы того качественного признака, по которому объекты сравниваются между
собой. Сложный качественный признак может пониматься экспертами по-разному, в
этом случае они могут оценивать объекты на основе несовпадающих частных
признаков.
Величина показателя согласованности
оказывается близкой к единице чаще всего в случаях, когда задача ранжирования
объектов тривиальна и в действительности нет необходимости в создании
экспертной группы для ее решения.
КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ
СПИРМЕНА.
Часто для обработки данных, полученных
с помощью шкалы порядка, используют коэффициент
rS ранговой корреляции Спирмена,
его рекомендуют применять в том случае, если одно измерение произведено по
шкале порядков, а другое — по шкале интервалов. Метод ранговой корреляции
Спирмена, является непараметрическим методом, он является универсальным и
работает с данными, измеренными в любых
шкалах, и прост в применении. Уникальность метода ранговой корреляции состоит в
том, что он позволяет сопоставлять не индивидуальные показатели, а
индивидуальные иерархии, или профили, что недоступно ни одному из других статистических
методов, включая метод линейной корреляции. Коэффициент ранговой корреляции Спирмена
рекомендуется применять в тех случаях, когда нам необходимо проверить, насколько совпадают индивидуальные ранговые
показатели у двух отдельных экспертов или у эксперта и группы экспертов.
Метод ранговой корреляции Спирмена
позволяет определить тесноту (силу) и направление корреляционной связи между
двумя признаками или двумя профилями (иерархиями) признаков.
Для подсчета коэффициента ранговой
корреляции Спирмена необходимо иметь два ряда значений, которые могут быть
проранжированы. Вначале показатели
ранжируются отдельно по каждому из признаков A,
B. Каждая из двух совокупностей
располагается в виде вариационного ряда с присвоением каждому члену ряда
соответствующего порядкового номера (ранга), выраженного положительным числом.
Одинаковым значениям ряда присваивают среднее ранговое число. Сравниваемые
признаки можно ранжировать в любом направлении как в сторону ухудшения качества
(ранг 1 получает самый большой, быстрый, умный и т. д. испытуемый), так и
наоборот. Главное, чтобы обе переменные
были проранжированы одинаковым способом. Как
правило, меньшему значению признака начисляется меньший ранг.
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА РАНГОВОЙ
КОРРЕЛЯЦИИ СПИРМЕНА.
Коэффициент ранговой корреляции
Спирмена находится по формуле:
rs = 1 – (6 ∑di2)/(N3 – N) (1),
где di – разность рангов для каждой i–пары из N наблюдений.
![]()

Коэффициент rS ранговой корреляции Спирмена изменяется от –1 до +1. Для подсчета коэффициента ранговой корреляции Спирмена rs необходимо определить разности di = xi - yi между рангами, полученными по обоим признакам. Затем эти значения di подставляем в формулу (1). Чем меньше разности между рангами, тем больше будет rs, тем ближе он будет к (+1). Если корреляция отсутствует, то все ранги будут перемешаны и между ними не будет никакого соответствия. Формула (1) составлена так, что в этом случае rs окажется близким к 0. В случае отрицательной корреляции низким рангам испытуемых по одному признаку будут соответствовать высокие ранги по другому признаку, и наоборот. Чем больше несовпадение между рангами испытуемых по двум переменным, тем ближе rs к (– 1).
Если в вариационных рядах для Xi и Yi встречаются члены ряда с одинаковыми ранговыми числами, то в формулу для коэффициента корреляции Спирмена необходимо внести поправки TX и TY на одинаковые ранги:
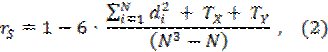

Где TX и TY вычисляются по формулам:
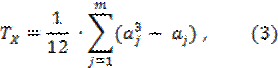
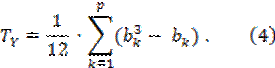

В формуле (3) m – количество групп в ранговом ряду X с одинаковыми ранговыми числами; Соответственно, a1, a2, …, am (aj > 1) – это объемы каждой группы с одинаковыми рангами в первом ранговом ряду X.
В формуле (4) p – количество групп в ранговом ряду Y с одинаковыми ранговыми числами. Соответственно, b1, b2, …, bp (bk > 1) – это объемы каждой группы с одинаковыми рангами во втором ранговом ряду Y.
При решении управленческих задач
структура и процесс решения проблем во многих случаях не могут быть достоверно
определены. Поэтому точность результатов решения не может превышать точности
принятых предположений. Это обстоятельство предопределяет выбор
соответствующего математического аппарата. Нет смысла применять более сложный
математический аппарат, поскольку это отнюдь не гарантирует получение более
точного результата. Использование логических методов и приемов в сочетании с
чисто математическими методами принятия решений позволяет принимать более
качественные решения и в тех случаях, когда численные оценки затруднены или
невозможны.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Балдин
К.В., Воробьев С.Н., Уткин В.Б. Управленческие решения: Учебник. – 2-е изд.
– М.: Издательско-торговая корпорация
«Дашков и К0», 2006, 496 с.
[2] Дульзон
А.А. Разработка управленческих решений: Учебник. – Томск: Изд-во Томского
политехнического университета, 2009. – 295 с.

[3] Смирнов Э.А. Управленческие
решения. (Серия «Вопрос-Ответ»). М.:
ИНФРА-М, 2001. – 264 с.
[4] Трофимова Л.А., Трофимов В.В.
Методы принятия управленческих решений: Учебное пособие. – СПб. : Изд-во
СПбГУЭФ, 2012. – 101 с.
[5] Черноруцкий И.Г. Методы принятия
решений. Учебное пособие. – СПб.: БХВ-Петербург, 2005. – 416 с., ил.
