Математические методы исследования экономики. Функции и графики в экономическом моделировании. Способы задания и исследования функций. Построение и анализ графиков функций. Графики в экономическом моделировании. Функция Торнквиста. Функция дохода. Функция спроса. Кривая безразличия. Теория потребительского спроса
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Математические методы исследования
экономики
Лекция 2
Тема лекции 2: «Функции и графики в экономическом моделировании»

Разделы лекции
1. Способы задания и исследования функций.
2. Построение и анализ графиков функций.
3. Графики в экономическом моделировании.

РАЗДЕЛ 1. СПОСОБЫ ЗАДАНИЯ И ИССЛЕДОВАНИЯ ФУНКЦИЙ.
Многочисленные наблюдения и
исследования показывают, что в окружающем нас мире величины (например,
цена какого-либо товара и величина спроса на этот товар, прибыль фирмы и объем производства этой фирмы, инфляция и
безработица и т.п.) существуют не
изолированно друг от друга, а напротив, они связаны между собой определенным
образом. Понятие функции или функциональной зависимости - одно из
основных математических понятий при помощи
которых моделируются взаимосвязи между различными величинами, количественные и
качественные отношения между различными экономическими характеристиками и показателями. Понятие
функции, как и понятие множества, относится к числу начальных
понятий, поэтому оно не определяется, а поясняется.
Говорят, что задана числовая функция f: A→B, если дан закон, согласно которому каждому значению х из некоторого числового множества А
ставится в
соответствие одно вполне определённое значение у из некоторого числового
множества В.
Функциональная зависимость между
величинами х и у символически
обозначается так: y=f(x), говорят, что х
- аргумент (независимая
переменная), а у- функция (зависимая переменная). Совокупность всех значений аргумента,
каждому из которых соответствует вполне
определенное значение функции, называется областью
определения функции. Множество значений, принимаемых у, называется областью
значений функции.
Функцию можно задавать различными
способами. Наиболее распространенные и важные среди них - задание функции
формулой, таблицей и графиком. При задании
функций, например, в программировании
используется также алгоритмический способ задания.
ПРИМЕР.
В качестве примера рассмотрим
взаимосвязь между ценой продукта,
которую мы обозначим через р и величиной спроса на этот продукт,
которую мы обозначим через q. Эта связь может быть, к примеру,
представлена следующей таблицей (рисунок 1), отражающей отрицательную взаимосвязь величин (убывание
величины спроса с возрастанием цены).
|
Цена продукта, p, руб. |
100 |
150 |
200 |
250 |
300 |
|
Величина спроса, q, тыс.шт. |
18 |
15 |
12 |
9 |
6 |

Рисунок 1.
Табличное задание функции.
Эта же взаимосвязь величин может быть
представлена в виде графика на
рисунке 2.
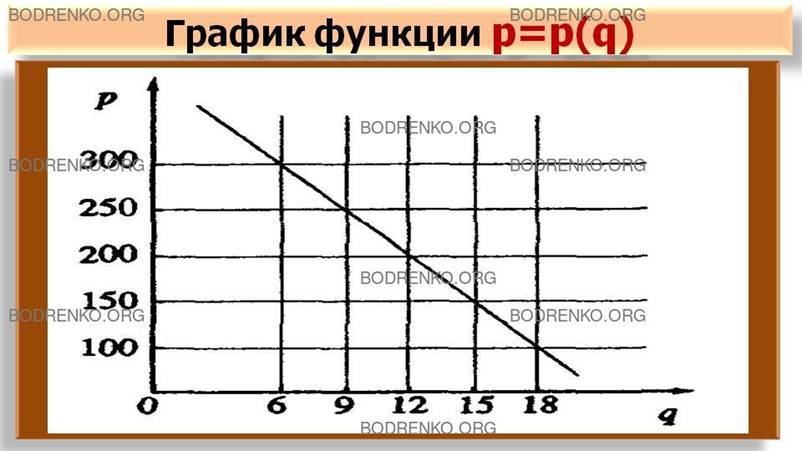
Рисунок 2. Графическое
задание функции.
ЧТО ТАКОЕ ГРАФИК ФУНКЦИИ?
ОПРЕДЕЛЕНИЕ.
Графиком функции y=f(x) называется геометрическое место (множество) точек на координатной плоскости XOY, имеющих координаты (х; f(x)), у которых абсциссами служат
рассматриваемые значения
независимой переменной х, а ординатами - соответствующие
значения функции y=f (x).
Для того, чтобы построить график
функции, имея ее табличное
представление, например график функции
спроса, достаточно отложить
значения величин, приведенных в таблице на
соответствующих координатных осях,
восстановить перпендикуляры к осям из точек,
соответствующих определенному значению цены или спроса, и нанести точки пересечения перпендикуляров на координатную плоскость.
Функциональная зависимость между
величинами x и у может быть задана также в виде формулы у = f(x) , в которой в
качестве f(x)
фигурирует конкретная функция. В данном случае зависимость между ценой и величиной спроса выражается формулой:
р = 400 - 50q/3
(или q = 24 - 0,06∙p).

Подставляя в последнюю формулу значения
цены, представленные в верхней строке таблицы, мы легко убедимся в
том, что в результате получаются соответствующие ценам величины спроса, представленные в нижней строке
таблицы.
Таким образом, зная формулу функции,
несложно получить табличное и графическое представление
этой функции.
СВОЙСТВА ФУНКЦИЙ.
Функции характеризуются рядом свойств,
к важнейшим из которых (для построения и исследования графиков) относятся:
четность, нули, периодичность, монотонность, ограниченность функции, наличие у
функций асимптот и обратной функции. Рассмотрим
вкратце эти свойства функций.
1.
ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ. Функция y=f(x) называется четной, если для любых значений аргумента x из области ее
определения A выполняется
равенство: f(-x) = f(x), "xÎA.
Например, y = |x| -
четная функция; y = cos (x) – четная функция.
Сумма, разность, произведение и частное четных функций есть функция четная.
ОПРЕДЕЛЕНИЕ. Функция y=f(x) называется нечетной, если для любого значения
аргумента x из области определения A функции выполняется равенство: f(-х) = -f(x), "xÎA.
К нечетным функциям относятся, например, функция y=sin (x); функция y = 3x.

Не всякая функция является либо четной,
либо нечетной. Например,
функция y = x/(x+4) не является ни четной, ни нечетной (так называемая, аморфная
функция).
Заметим, что если функция y=f(x) четная
или нечетная, то область ее определения симметрична относительно начала координат O. Поэтому, например, функции y = exp (x); y=lg (x) и т.д. не могут быть ни четными, ни нечетными.
Сумма и разность нечетных функций есть
функция
нечетная, а произведение и частное
нечетных функций — функция
четная.
График четной функции симметричен
относительно оси 0Y, а
нечетной - относительно центра О.
2. НУЛИ ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ. Нулем функции y=f(x) называется такое значение
аргумента x, при котором значение функции равно нулю: f(х) = 0.
Графически нулями функции являются
точки пересечения графика
функции с осью абсцисс. Например,
нулями функции y= (х-1)(х+2) будут корни уравнения у = 0, т.е. х = 1
и х = -2.
3. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ. Функция у=f(x) называется периодической,
если существует число T≠0 такое, что для каждого значения аргумента
х из области ее определения A имеет место равенство: f(x+T) = f(х), "xÎA. Число T называют периодом этой функции.
Приведем примеры периодических функций.
y = sin(x); y = cos(x); (для них
наименьший положительный
период равен 2«пи»: T= 2π).
y = tg(x); y = ctg(x) (для них наименьший положительный
период равен «пи»:T = π).

4. МОНОТОННЫЕ ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ. Функция у=f(x) называется монотонно возрастающей на некотором промежутке (a,b), если для любых значений аргумента х из этого промежутка, большему значению аргумента соответствует
большее значение функции, т.е. если х1< х2,
то f(x1)< f(x2).
ОПРЕДЕЛЕНИЕ. Функция у=f(x) называется монотонно убывающей на некотором промежутке (a,b), если для
любых значений х из этого промежутка, большему значению аргумента
соответствует меньшее значение функции, т.е. если x1< х2, то f(x1)>f (x2).

Как возрастающие, так и убывающие
функции называются монотонными функциями.
5. АСИМПТОТЫ.
Асимптотой графика функции называется
прямая,
к которой сколь угодно близко
приближается график данной функции при стремлении аргумента к бесконечности или
к некоторому числу а (в случае вертикальной асимптоты). Асимптоты могут быть вертикальными, горизонтальными и наклонными.
Вертикальная асимптота - это прямая х=
а, если lim{x→a} f(x) = ∞.
Горизонтальная асимптота - это прямая у
= b, если lim{x→∞} f(x) = b.
Наклонная асимптота - это прямая у = kх
+ b, если lim{x→∞}(f(x)
— kx) = b.
Угловой
коэффициент k находится путем вычисления предела
lim{x→∞}(f(x)/x)
6. ОГРАНИЧЕННЫЕ ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ. Функция y=f(x) называется ограниченной сверху
(снизу), если существует такое число М, что для всех значений аргумента х из области
определения A функции
выполняется неравенство: f(x) < M, "xÎA (f(x) > М, "xÎA) (рисунок 3 а, б).
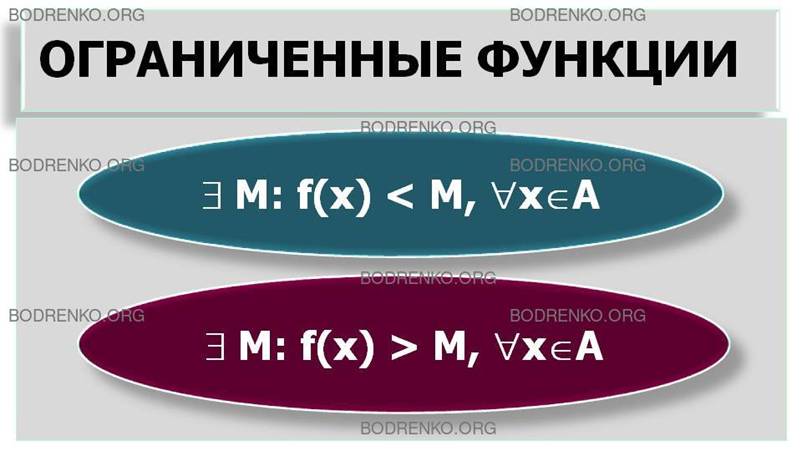
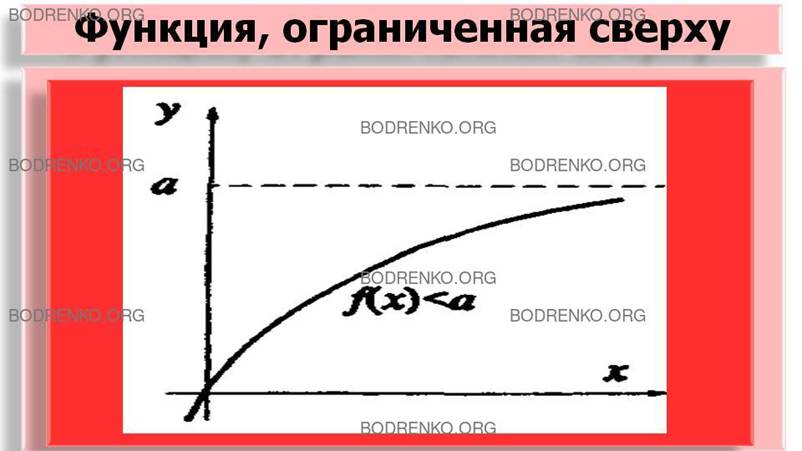
Рисунок 3а.
Функция, ограниченная сверху.
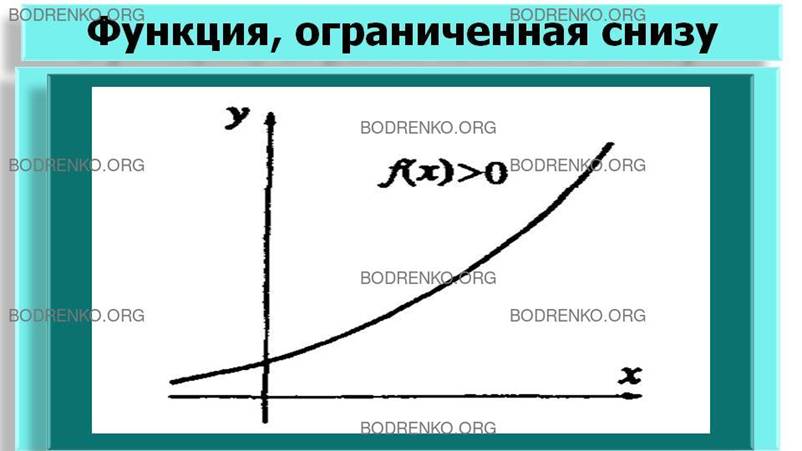
Рисунок 3б.
Функция, ограниченная снизу.
ОПРЕДЕЛЕНИЕ. Функция y=f(x) называется ограниченной, если существует такое
число
M> 0, что для всех значений аргумента х из области определения A функции выполняется неравенство: |f(x)| < М, "xÎA
(рисунок 3в).
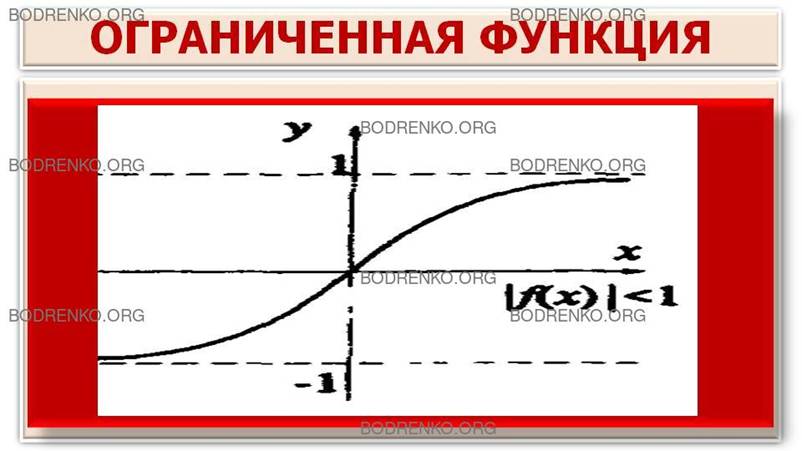
Рисунок 3в.
Ограниченная функция.
7. ОБРАТНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК.
Дана функция y = f(x). Выразим x как
некоторую функцию от у: х= g(y), т.е. представим у как аргумент; х - как функцию. Тогда
функция х= g(y) называется обратной по отношению к функции у = f(x), если при
подстановке её
вместо аргумента получаем
тождественное равенство: y ≡ = f(g(y)). Отметим, что не всякая функция имеет обратную.

Равенство функций называется
тождественным, если оно справедливо при всех значениях аргумента из области
определения.
ПРИМЕР.
Дана функция у= x/3 + 1. Разрешим ее относительно х. Мы имеем: x = 3y - 3. Функция х= 3y – 3 будет обратной по отношению к функции у= x/3 + 1,
так как выполняется тождество y = (3y – 3)/3 + 1.

Отметим, что область определения и множество значений функции
y= f(x) и функции х= g(y), обратной к ней, меняются
ролями.
8. СЛОЖНАЯ ФУНКЦИЯ.
Функция, заданная в виде у =f(h(x)), называется сложной функцией аргумента х или суперпозицией функций f и h. Сложную функцию часто записывают в виде у = f(u), где u = h(x). При этом аргумент х называют независимой переменной, а u - промежуточным аргументом.

9. НЕЯВНАЯ ФУНКЦИЯ.
Функция, заданная в виде уравнения F(x,y) = 0, не разрешенном относительно y,
называется неявной функцией х.
РАЗДЕЛ 2. ПОСТРОЕНИЕ И АНАЛИЗ ГРАФИКОВ ФУНКЦИЙ.
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ МЕТОДОМ ПРЕОБРАЗОВАНИЯ
ГРАФИКОВ.
Для построения графиков функция имеется
несколько способов, одним из которых является преобразование графика подходящей элементарной функции до его совпадения
с графиком данной функции. Этот
способ особенно удобен, если данная функция может быть выражена через одну из элементарных функций в виде: f(x) = k1∙G(k2∙(x – a)) + b, где G – некоторая элементарная функция, k1, k2, a, b – некоторые константы.
Тогда график этой функции будет представлять комбинацию
сдвигов (горизонтальных и вертикальных), а также сжатий-растяжений графика соответствующей элементарной функции. Рассмотрим более подробно приемы построения графиков функций через
их преобразования.
КАКИЕ ОСНОВНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ СУЩЕСТВУЮТ?
ОСНОВНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ.
1. Вертикальный сдвиг f(x) → f(x) + b.
2. Горизонтальный сдвиг f(x) → f(x + a).
3. Комбинированный сдвиг f(x) → f(x + a) + b.
4. Отражение:
а) функции f(x) → -f(x) , б) аргумента f(x) → f(-x) .
5. Растяжение (k > 1) / Сжатие (0 < k <
1):
а) функции f(x) → k f(x) , б) аргумента f(x) → f(k x) .
6. Взятие модуля:
а) функции f(x) → |f(x)| , б) аргумента f(x) → f(|x|).
1) Построить график функции y = f(x) + b, если
дан график функции y = f(x).
Если b > 0, то каждая ордината увеличится на величину b и график «сдвинется вверх» вдоль оси OY. Если b < 0,то график «сдвинется
вниз»
на величину b вдоль оси OY (рисунок 4).
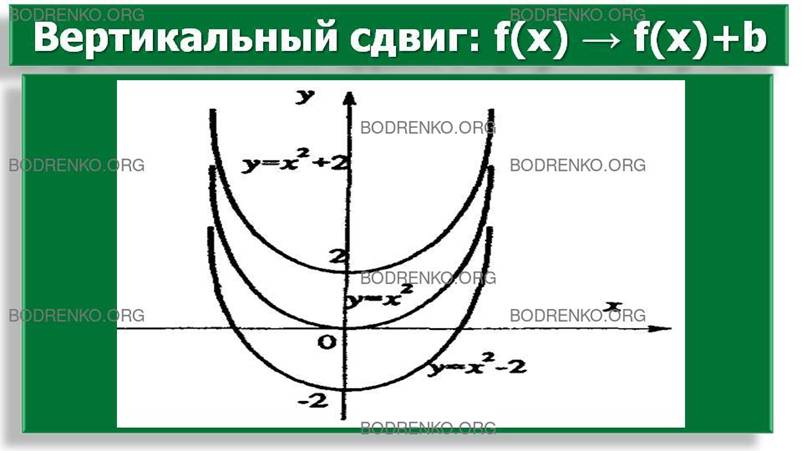
Рисунок 4. Вертикальный сдвиг
графика функции.
2) Построить график функции y = f(x + a), если задан
график функции y = f(x).
Имеем f(x0) = f(x1 + a) = y0. Откуда следует, что x0 = x1 + a , следовательно, x1 = x0 – a .
Если а > 0, то точка x0 переходит в точку x1 путём сдвига влево на а единиц.
Если а < 0, то точка x0 переходит в точку
x1 путём сдвига вправо на |a| единиц (рисунок 5) .
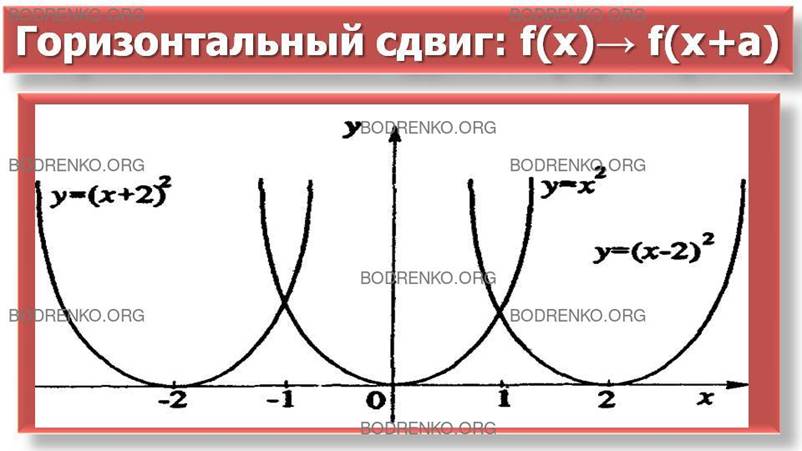
Рисунок 5. Горизонтальный
сдвиг графика функции.
3) Дан график функции
у = f(x) (на рисунке 6 он обозначен пунктиром). Построить график функции y = f(x+a) + b.
Строим новую систему координат x’O’y’ с началом в точке О’ с координатами (-а; b)
и осями координат O’x’параллельной оси Ox ,
и O’y’параллельной оси Oy. Относительно этих осей строим
график y = f(x). Полученный график будет искомый в системе координат
xOy (рисунок 6).

Рисунок 6. Комбинированный
сдвиг графика функции.
4а) Построить график у
= -f(x), если дан график у = f(x).
Каждому значению независимой переменной
х будет соответствовать противоположное по знаку значение ординаты у. Следовательно, график новой функции будет зеркальным
отражением прежней функции относительно оси Ох (рисунок 7а).
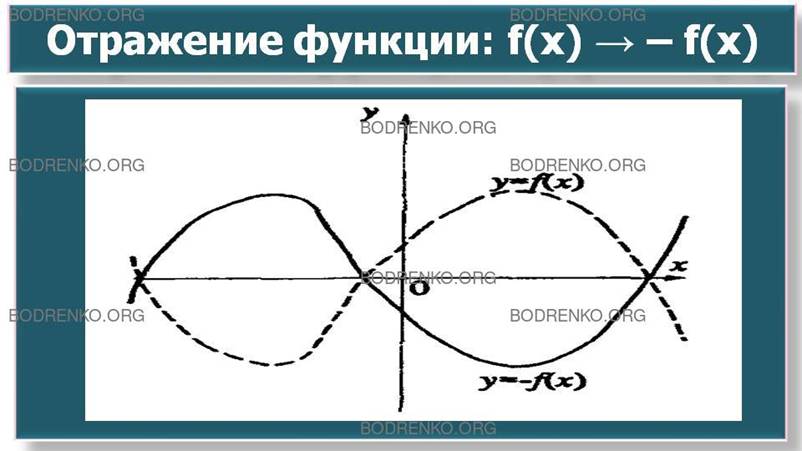
Рисунок 7а.
Отражение функции.
4б)
Построить график функции y = f(-x), если задан график функции y = f(x).
Каждому значению ординаты у будет
соответствовать противоположное
по знаку значение независимой переменной х. Следовательно,
график новой
функции будет зеркальным отражением прежней функции относительно оси ОY
(рисунок 7б).
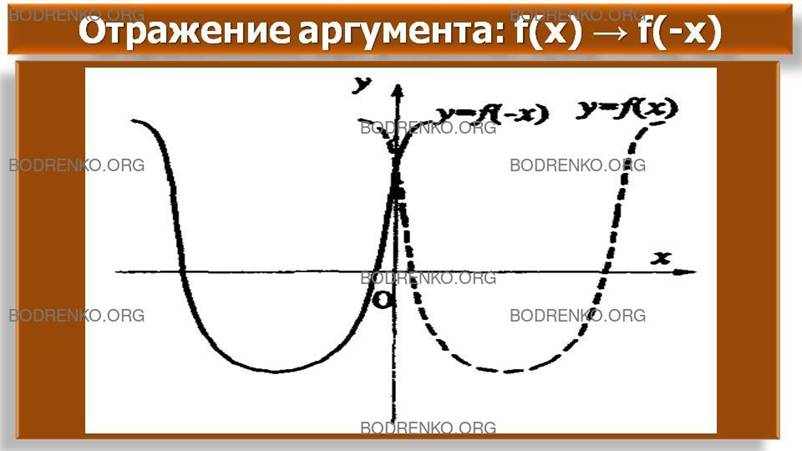
Рисунок 7б.
Отражение аргумента.
5а) Построить график функции y = kf(x), если задан график функции y = f(x).
Если k> 1,то каждая ордината увеличится в k
раз, и
график «растянется» вдоль оси Оу (рисунок 8). Если k <
1, то график «сожмется» в k раз вдоль оси Oy.
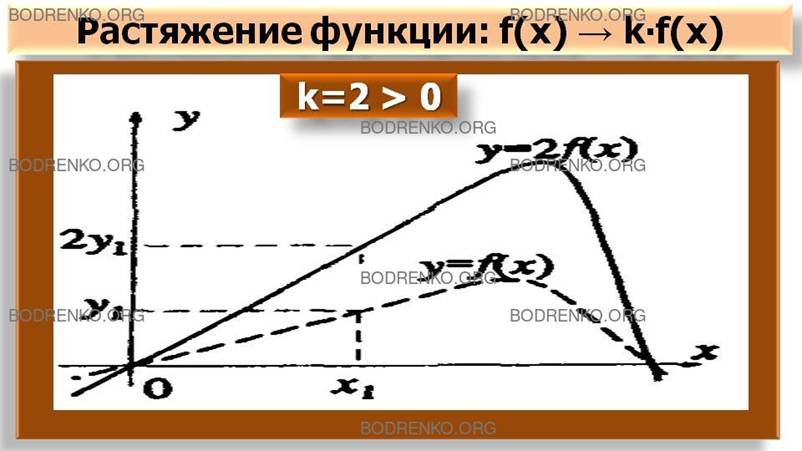
Рисунок 8.
Растяжение (сжатие) функции.
5б) Построить график функции y = f(k x), если задан график y = f(x).
Если k > 1, то график «сожмется» в k раз вдоль оси Ох. Если k < 1, то график «растянется» в k раз
вдоль оси Ох (рисунок 9).
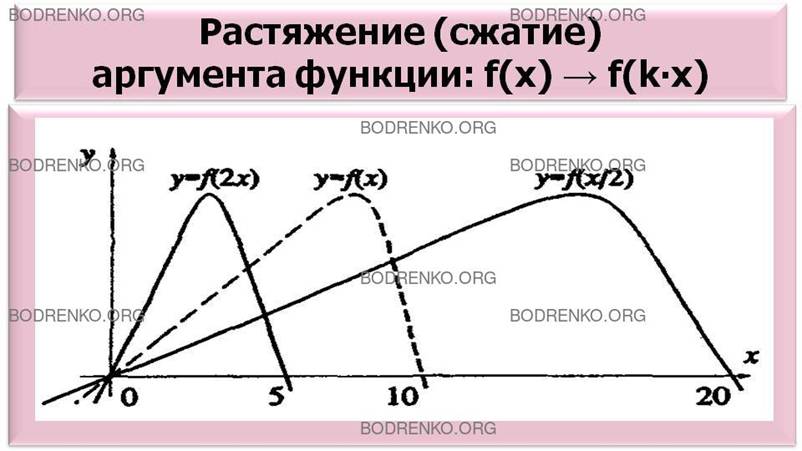
Рисунок 9.
Растяжение (сжатие) аргумента.
6а)
Пусть дан график функции у = f(x) (пунктирный). Надо построить график функции y = |f(x)|.
Если f(x) > 0, то |f(x)| = f(x), следовательно, часть графика функции у = f(x), расположенную в верхней полуплоскости,
надо оставить без изменения.
Если f(x) < 0, то |f(х)| = - f(x), значит часть графика, расположенную в нижней полуплоскости, надо отобразить в верхнюю полуплоскость
симметрично относительно оси OX (рисунок 10а).
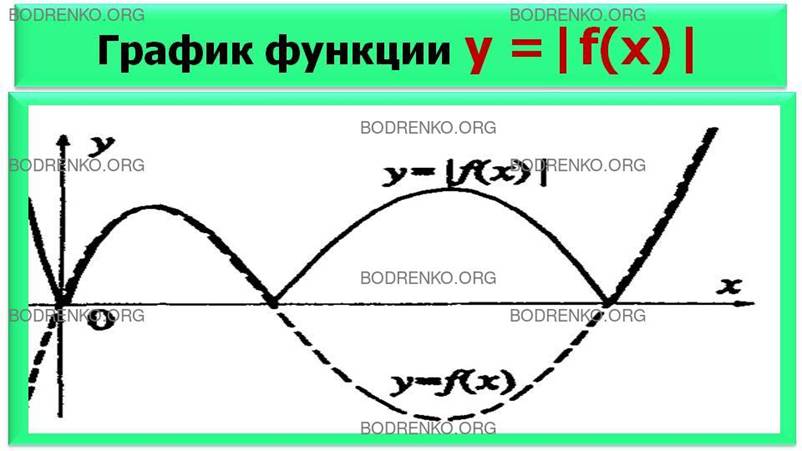
Рисунок 10а. График
функции y = |f(x)|.
6б) Пусть дан график функции
у = f(x) (пунктирный). Надо построить
график функции y =f (|x|).
Эта функция y =f (|x|) четная, поэтому график ее симметричен относительно оси Оу.
Но при х > 0 имеем f(|х|) = f(х), т.е. при х > 0
графики функций y = f(|х|) и y = f(х)
совпадают.
Итак, для построения графика нужно часть графика, расположенную в правой полуплоскости,
отобразить в левую
полуплоскость симметрично относительно оси OY (рисунок 10б).
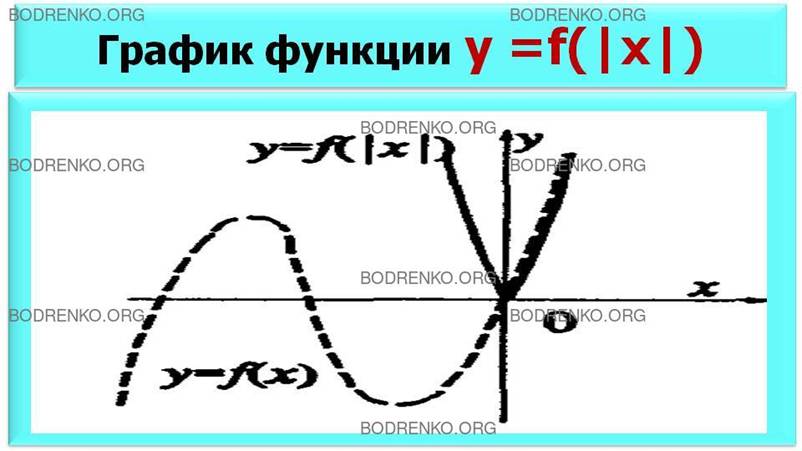
Рисунок 10б.
График функции y = f(|x|).
ПРИМЕР ПОСТРОЕНИЯ И АНАЛИЗА ГРАФИКА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.
Дана дробно-линейная функция у = (ах + b)/(cx + d).
Данная функция определена при x ≠ –d/c. Множество значений функции (-∞, +∞). Преобразуем выражение, задающее функцию, выделением целой части:
y = ((a/c)cx
+b)/(cx+d) =((a/c)(cx+d) – (ad)/c +b)/(cx+d)= a/c + (b-(ad)/c)/(cx+d)= a/c +
((bc-ad)/c∙c)/(x+d/c).

Введем обозначения: y0=a/c, x0= –d/c, k=(bc-ad)/c∙c.
В этих обозначениях можно записать дробно-линейную функцию в следующем виде:
y = y0 + k/(x –
x0).

Из такой формы записи сразу видно, что графиком дробно-линейной
функции у=(ах+b)/(cx+d) является гипербола, центр которой
смещен в точку (x0, y0), то есть в точку (–d/c, a/c).
Если у гиперболы у =k/x асимптотами
были оси координат OX, OY, то у дробно-линейной
функции у = (ах + b)/(cx + d) асимптотами будут прямые x= - d/c, у = a/c. Знак числа k указывает, в каких четвертях относительно асимптот будет лежать
гипербола на координатной плоскости, и во сколько
раз график надо
сжать или растянуть.
В качестве примера построим график функции у = (2x+4)/(x+3).
1. Выделим целую часть. Мы получим: у = 2 – 2/(x+3).

2. На координатной плоскости во вспомогательной системе координат x’O’y’строим график функции y’ = 2/x’. Он расположен во второй и четвертой
четвертях (рисунок 11).
3. Построим исходную систему
координат хОу с помощью вспомогательной системы координат х’O’y’, осуществив параллельный перенос осей координат O’X’ и O’Y’ (на 3 единицы вправо и на 2 единицы вниз). В системе хОу построенный ранее график будет графиком заданной функции у = (2x+4)/(x+3).
Причем, действительно, прямые: x= –3 и у= 2 являются асимптотами.
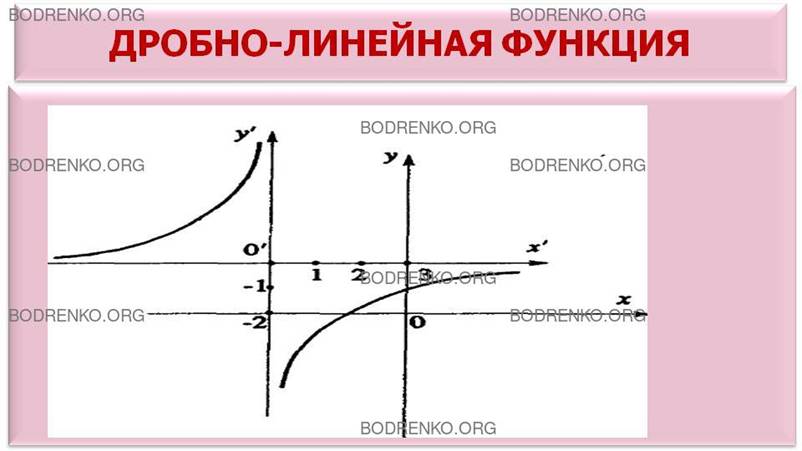
Рисунок 11. График
дробно-линейной функции y = (2x+4)/(x+3).
В качестве экономического примера дробно-линейной зависимости рассмотрим одну из функций Торнквиста: x(I) = (αI)/(I+β). (Здесь I - аргумент).
Функция x(I) описывает зависимость величины спроса
на предметы первой
необходимости от величины дохода. Преобразуем эту функцию к виду:
x(I) = (α(I + β – β))/(I+β) = α – (α∙β)/(I+β).

Таким образом, задача построения
графика этой
функции сводится к преобразованию графика гиперболы x=1/I путем
ее растяжения в α∙β раз, инвертирования отражения относительно горизонтальной оси и сдвига на
величину α вдоль оси X и на величину (–β) вдоль
оси I.
Например, для
случая α=2, β=3 получим функцию Торнквиста x(I) = 2I/(I+3). Построение графика этой функции аналогично предыдущему
примеру. В частности, прямые x= –β, y= α являются
асимптотами.
РАЗДЕЛ 3. ГРАФИКИ В ЭКОНОМИЧЕСКОМ МОДЕЛИРОВАНИИ.
ФУНКЦИЯ ПОТРЕБЛЕНИЯ И ЛИНИЯ БЮДЖЕТНОГО
ОГРАНИЧЕНИЯ.
В теории потребительского спроса на два
блага х и у (к примеру,
исследуемое х и все остальные у)
предпочтения потребителя
описываются кривой безразличия U(x,y) =
U0,
а бюджетное ограничение
(расходы потребителя ≤
его дохода) в случае, когда потребитель тратит весь свой доход на рассматриваемые
блага: х ∙р1
+ у ∙р2
= I, где I - доход потребителя, а р1 и р2 - цены благ х и у соответственно. Для того, чтобы построить графики этих неявно заданных функций
y(x) в системе координат, где по оси
абсцисс отложена величина блага х, а по оси ординат - у, нужно выразить в явном виде величину у
как функцию x для
обеих зависимостей. Сделаем это для простейшей функции полезности U(x,y)=xy.
Для уровня полезности (благосостояния)
U0
и дохода I получаем следующие функции:
y = U0/x, y = I/p2 — (x∙p1)/p2.

Графиком первой из этих функций (кривой безразличия)
является гипербола, а графиком второй (бюджетного ограничения) - прямая линия, имеющая
отрицательный угловой коэффициент («наклон»), равный по абсолютной величине относительной цене блага x и точку
пересечения с осью ординат I/p2,
соответствующую количеству блага у, которое можно
приобрести по цене p2, если потратить на него весь доход I (рисунок 12).
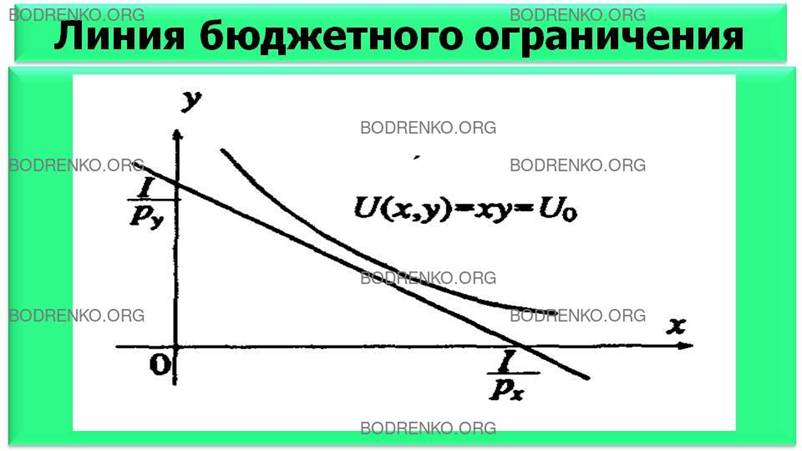
Рисунок 12. Линия
бюджетного ограничения.
КРИВЫЕ СПРОСА И ПРЕДЛОЖЕНИЯ.
Другим примером функций в экономике
служат функции спроса и предложения p(q), выражающие связь цены блага и
величины спроса или
предложения блага при постоянных вкусах потребителей, ценах на другие блага и других параметрах.
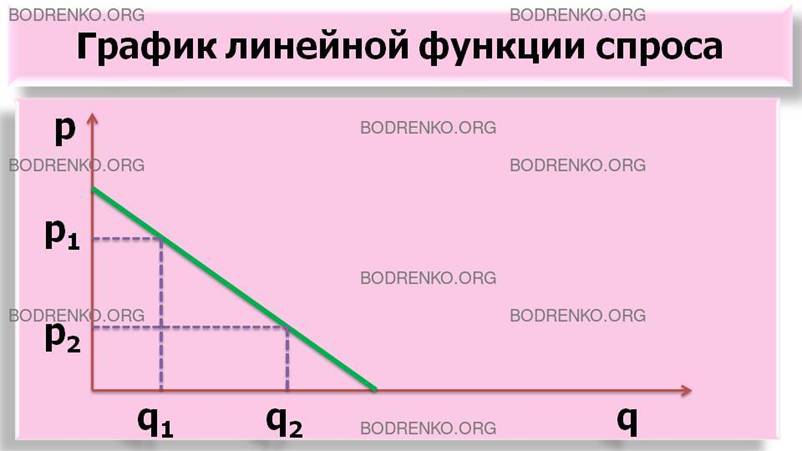
Пример графика линейной
функции спроса приводился в первом разделе
этой лекции (рисунок 2).
Аналогично строится и график функции
предложения, но в отличие от функции
спроса он отражает положительную связь переменных p и q (рисунок 13).

Рисунок 13. Кривые спроса и
предложения.
ЗАВИСИМОСТИ ВЕЛИЧИНЫ СПРОСА ОТ ДОХОДА.
В модели потребительского спроса
используются также функции Торнквиста, моделирующие связь между величиной
дохода (I) и величиной
спроса потребителей (х) на:
а) малоценные товары
x = αI(I+β)/(I∙I+γ) ;
б) товары первой необходимости
x = αI/(I+β) ;
в)
товары второй необходимости
(относительной роскоши)
x = α(I–γ)/(I+β) ;
г) предметы роскоши
x = αI∙(I–γ)/(I+β).
Соответствующие им графики приведены на
рисунке 13.
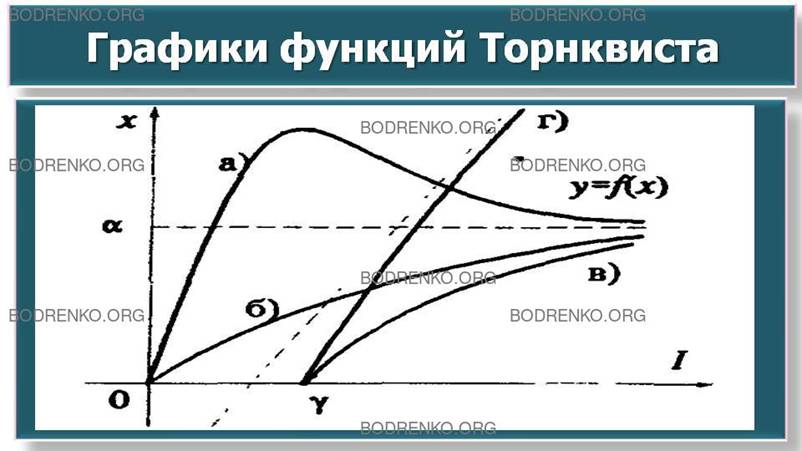
Рисунок 13. Графики
функций Торнквиста.
ГРАФИКИ ЗАВИСИМОСТИ ИЗДЕРЖЕК И ДОХОДА
ОТ ОБЪЕМА ПРОИЗВОДСТВА.
Рассмотрим функции издержек C(q) и дохода фирмы R(q) =qp(q) в
зависимости от объема производства
q. Поведение функции дохода определяется функцией спроса p(q),
рассмотренной выше. Поэтому рассмотрим более подробно поведение функции издержек. В типичном случае издержки фирмы велики при
небольшом объеме производства q и вначале растут быстрее, чем
доход. С увеличением объема производства скорость роста
издержек уменьшается и в какой-то момент они сравниваются с доходом и фирма
начинает получать прибыль. При увеличении объема производства прибыль увеличивается, достигая
максимума
при оптимальном значении q. При
дальнейшем увеличении объема производства
издержки снова начинают расти быстрее дохода (исчерпаны эффективные ресурсы,
нужны дополнительные помещения,
сырье, квалифицированная рабочая сила) и прибыль фирмы
уменьшается,
достигая отрицательных
значений при достаточно
больших объемах производства.
Типичные графики функций дохода, издержек и прибыли приведены на рисунке 14. Им, например, могут
соответствовать функции:
R(q) = q(a — bq), C(q) = cq – q(d–eq)q.

Рисунок 14. Графики функций издержек C(q), дохода R(q) и прибыли П(q).
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Замков О.О., Толстопятенко А.В.,
Черемных Ю.М. Математические методы в экономике: Учебник. 2-е изд. - М.: МГУ
им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. — 368 с.
[2] Фомин Г. П. Математические
методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и
доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

[3] Шелобаев
С. И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. —
М.: ЮНИТИ - ДАНА, 2001. - 367 с.
[4] Шикин Е.
В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб.
пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический
университетский учебник»).
[5]
Экономико-математические методы и прикладные модели: Учебное пособие для вузов/
В.В. Федосеев, А.Н. Гармаш, Д.М.
Дайитбегов и др.; Под ред. В.В. Федосеева. — М.: ЮНИТИ, 1999. - 391 с.
