Математическое моделирование экономических систем. Линейные динамические модели макроэкономики с непрерывным временем. Применение теории обыкновенных дифференциальных уравнений в задачах экономики. Глобальные имитационные модели системной динамики. Модели системной динамики «Мир-1», «Мир-2», «Мир-3»
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Математическое моделирование экономических систем
Лекция 8
Тема лекции 8: «Линейные динамические модели макроэкономики
с непрерывным временем»

Разделы лекции:
1. Применение теории
обыкновенных дифференциальных уравнений в задачах экономики.
2. Глобальные имитационные
модели системной динамики.
3. Модели системной динамики «Мир-1»,
«Мир-2», «Мир-3».

РАЗДЕЛ 1. ПРИМЕНЕНИЕ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ В ЗАДАЧАХ ЭКОНОМИКИ.
ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ.
Дифференциальные уравнения занимают особое
место в математике и имеют многочисленные приложения в большом спектре наук.
Исследования природных процессов и изучение закономерностей общественных
процессов приводят к построению математических моделей, основой которых являются
дифференциальные уравнения.
В дифференциальных уравнениях неизвестная
функция содержится вместе со своими производными. Основной задачей теории
дифференциальных уравнений является изучение функций, представляющих собой
решения этих уравнений.
Задачи, решаемые экономической
наукой и практикой, делятся,
в зависимости от учета фактора времени, на статические и динамические. Статика изучает состояния
экономических объектов, относящиеся к определенному моменту или периоду
времени, без учета
изменения их параметров во времени. В динамических задачах
отражается не только зависимость переменных от времени, но и их
взаимосвязи во времени. Например, динамика инвестиций определяет динамику величин основного
капитала, что в свою очередь является важнейшим фактором
изменения объема выпуска.
Время в экономической динамике
может рассматриваться как непрерывное или дискретное.
Непрерывное время удобно для моделирования, так как
позволяет использовать аппарат дифференциального исчисления и дифференциальных
уравнений. Дискретное
время удобно для приложений, поскольку статистические данные
всегда дискретны и относятся к конкретным единицам времени.
Для дискретного времени может использоваться аппарат разностных уравнений. Заметим, что большинство известных моделей экономической динамики существуют как в непрерывном, так и в дискретном вариантах. В обоих вариантах для них могут быть получены, как правило, аналогичные результаты, и уровень сложности самих моделей примерно одинаков.
В экономической теории важным является понятие равновесия, то есть такого состояния объекта, которое он сохраняет при отсутствии внешних воздействий. Задачи экономической динамики включают как описание процессов выхода к состоянию равновесия, так и процессов трансформации самого этого состояния под воздействием внешних сил.
Рассмотрим простую экономическую систему в состоянии равновесия и опишем движение такой системы в непрерывном случае. Покажем, что динамика системы описывается с помощью дифференциального уравнения.
Дифференциальное уравнение связывает изменения показателя (пусть наша система описывается одним показателем x(t), или просто х) со скоростью его движения х't, или ẋ Будем считать, что скорость изменения показателя x пропорциональна величине его отклонения от равновесного значения xE. Иными словами, чем дальше показатель отклонился от равновесного значения, тем быстрее он стремится вернуться к нему. Если в уравнении присутствует только первая производная x по времени, а сама связь линейна, то это линейное дифференциальное уравнение. Пусть оно имеет, например, следующий вид:
x't = k∙(x – xE),
где k – некоторый коэффициент. В этом уравнении k∙xE – свободный член; без него уравнение будет иметь вид:
x't = к∙x,
это уравнение называется однородным и его общее решение x = С∙ekt.
Исходное неоднородное уравнение имеет частное решение x = xE (если величина x находится в состоянии равновесия), а общее его решение есть сумма любого частного решения и общего решения однородного уравнения, то есть х = xE+ c∙ekt. Учитывая, что при t = 0 величина x равна x(0), получаем C = x(0) — xE .
Тогда
x(t) = xE + (x(0)
— xE)ekt.

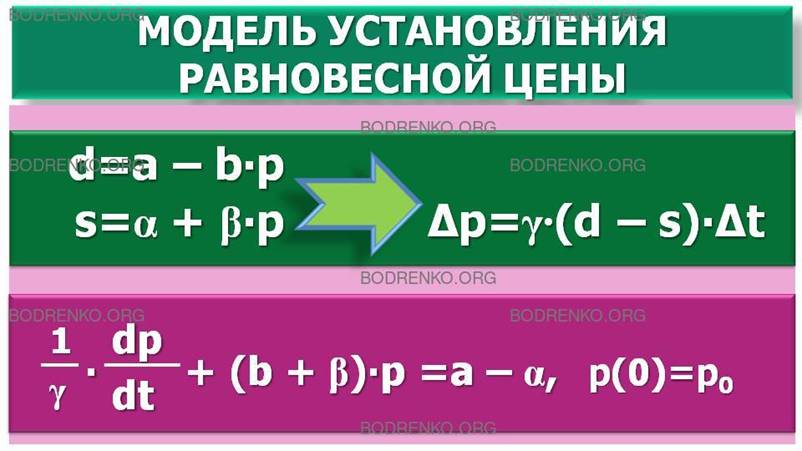
МОДЕЛЬ УСТАНОВЛЕНИЯ РАВНОВЕСНОЙ ЦЕНЫ.
В модели рассматривается рынок одного товара, время t считается непрерывным, спрос d и предложение s линейно зависят от цены:
d = a — b∙p, s = α + β∙p,
где
a> α, a>0, b>0, α >0, β>0.
Основное предположение модели состоит в том, что изменение цены пропорционально превышению спроса над предложением:
∆p = γ∙(d – s)∙∆t, где γ > 0.
То есть в случае действительного превышения спроса над предложением цена возрастает, в противном случае — падает.
Из основного предположения модели вытекает следующее дифференциальное уравнение для цены:
(1/γ)∙(dp/dt) + (b+β)∙p=(a – α),
и p(0) = p0.
т.е. процесс описывается линейным дифференциальным уравнением первого порядка.
Равновесная цена pE =(a – α)/(b+β)
(точка пересечения прямых спроса и предложения).
МОДЕЛЬ ОСВОЕНИЯ ВВЕДЕННЫХ ПРОИЗВОДСТВЕННЫХ МОЩНОСТЕЙ.
Обозначим через х (х = const) введенную производственную мощность, а через y(t) — фактическое производство на базе этой мощности в момент времени t (фактическое использование мощности, y(t) < x).
Сделав предположение, что прирост производства пропорционален недоиспользованной мощности:
∆у = у∙(x – у)∙∆t,
приходим к линейному дифференциальному уравнению:
T∙(dy/dt) + у = х , (1)
где T = 1/y, у(0) = у0 , у0 <х.

В соответствии с теорией линейных дифференциальных уравнений общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и частного решения неоднородного.
Общее решение однородного уравнения
T∙(dy/dt) + y = 0 (2)
имеет вид:
y = C∙eλt
Подставив его в (2), получим:
(T∙λ+1)∙y = 0.
Но y ≠ 0, поэтому приходим к характеристическому уравнению (относительно x):
T∙λ+1 = 0,
Отсюда λ= (-1/T).

Поскольку частным решением
неоднородного уравнения (1)
является у = х, то общее решение этого уравнения примет вид:
y = x + C∙e-t/T
Константу C находим из начального условия:
y(0) = x + C= y0, C = y0 – x.
Поэтому окончательно имеем
y (t) = x + (y0 – x)∙e-t/T.

Переходный процесс освоения производственных мощностей, описываемый этим решением, завершается выходом на заданный размер мощности
lim y(t) = х.
t→∞
При y0 = 0 решение примет вид:
y(t) = x∙(1 — e-t/T).
На этой лекции мы также рассмотрим
следующий пример применения теории дифференциальных уравнений в непрерывной модели
экономики, где независимой переменной является время t. Такие модели достаточно эффективны при исследовании эволюции
экономических систем на длительных интервалах времени; они являются предметом
исследования экономической динамики.
МОДЕЛЬ РЫНКА С ПРОГНОЗИРУЕМЫМИ ЦЕНАМИ.
Рассмотрим модель рынка с прогнозируемыми
ценами. В простых моделях рынка спрос и предложение обычно полагают зависящими
только от текущей цены на товар. Однако спрос и предложение в реальных
ситуациях зависят еще и от тенденции ценообразования и темпов изменения цены.
В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и
второй производными функции цены P(t).
Рассмотрим конкретный пример. Пусть функции спроса D и предложения S имеют следующие зависимости
от цены Р и ее производных:
D(t) = 3P′′ –
P′ – 2P +18,
S(t) = 4P′′ +
P′ + 3P + 3. (4)
Принятые в (4) зависимости вполне
реалистичны: поясним это на слагаемых с производными функции цены.
1. Спрос
"подогревается" темпом изменения цены: если темп растет (Р" > 0), то рынок увеличивает интерес
к товару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому
слагаемое с первой производной функции цены входит со знаком минус.
2. Предложение в еще большей
мере усиливается темпом изменения цены, поэтому коэффициент при Р"
в функции S(t) больше,
чем в D(t).
Рост цены также увеличивает предложение, потому слагаемое, содержащее Р', входит в выражение для S(t) со знаком плюс.
Требуется установить
зависимость цены от времени. Поскольку равновесное состояние рынка
характеризуется равенством D = S, приравняем правые части уравнений (4). После приведения подобных
получаем
P′′ + 2P′ + 5P = 15. (5)

Соотношение (5) представляет
линейное неоднородное дифференциальное уравнение второго порядка относительно
функции P(t).
Как было установлено в предыдущем пункте,
общее решение такого уравнения состоит из суммы какого-либо его частного
решения и общего решения соответствующего однородного уравнения
P′′ + 2P′ + 5P = 0. (6)
Характеристическое уравнение имеет вид
k2 + 2k + 5 = 0.
Его корни — комплексно-сопряженные числа: k1,2 = -1 ± 2i, и, следовательно, общее
решение уравнения (6) дается формулой
Pод(t) = e–t (C1 cos 2t + C2
sin 2t),
где С1
и С2 — произвольные
постоянные.

В качестве частного решения неоднородного
уравнения (5) возьмем решение Р = Pst —
постоянную величину как установившуюся цену. Подстановка в
уравнение (5) дает значение Pst:
Pst = 3.
Таким образом, общее решение уравнения (5)
имеет вид
P(t)
= 3 + e-t (C1 cos
2t + C2 sin 2t). (7)

Нетрудно видеть, что P(t) ![]() Pst = 3 при t
Pst = 3 при t ![]()
![]() , т.е. все интегральные кривые имеют горизонтальную асимптоту Р =
3 и колеблются около нее. Это означает, что все цены стремятся к
установившейся цене Pst с колебаниями около нее, причем амплитуда этих
колебаний затухает со временем.
, т.е. все интегральные кривые имеют горизонтальную асимптоту Р =
3 и колеблются около нее. Это означает, что все цены стремятся к
установившейся цене Pst с колебаниями около нее, причем амплитуда этих
колебаний затухает со временем.
Частные
решения: задача Коши и смешанная задача.
Приведем частные решения этой задачи в двух
вариантах: задача Коши и смешанная задача.
1. Задача
Коши. Пусть
в начальный момент времени известна цена, а также тенденция ее изменения. Т.е.
при t=0
P(0) =
4, P′(0) = 1.
Подставляя первое условие в формулу общего
решения (7), получаем Р(0) = С1 + 3 = 4, откуда С1 = 1, т.е.
имеем
P(t)
= 3 + e–t (cos 2t + C2
sin 2t). (8)
Дифференцируя, имеем отсюда
P′(t)
= e–t [(2C2 – 1) cos
2t – (C2 +2) sin 2t].
Теперь реализуем второе условие задачи Коши:
Р'(0) = 2C2 — 1 = 1, откуда C2 = 1. Окончательно получаем, что
решение задачи Коши имеет вид
P(t)
= 3 + e–t (cos 2t + sin 2t).

или в более удобной форме:
![]()
2. Смешанная
задача.
Пусть в начальный момент времени известны цена и спрос. Т.е.
при t=0
P(0) = 4, D(0) = 16.
Поскольку первое начальное условие такое же,
как и в предыдущем случае, то имеем и здесь решение (18). Тогда производные
функции Р(t) выражаются формулами
P′(t)
= e–t [(2C2 – 1) cos
2t – (C2 +2) sin 2t].
P′′(t)
= –e–t [(4C2 +3) cos 2t – (3C2 –5) sin 2t].
Отсюда Р'(0) =2C2 - 1 и Р"(0) =
-4C2 - 3. Подставляя эти равенства
во второе условие задачи, т.е. D(0) = 16, имеем с учетом вида D(t) из первой формулы (4): С2
= -1. Итак, решение данной задачи имеет вид
P(t) = 3 + e–t (cos 2t – sin 2t),

или в более удобной форме:
![]() .
.
Интегральные кривые, соответствующие задачам
1 и 2, изображены на рисунке 1.
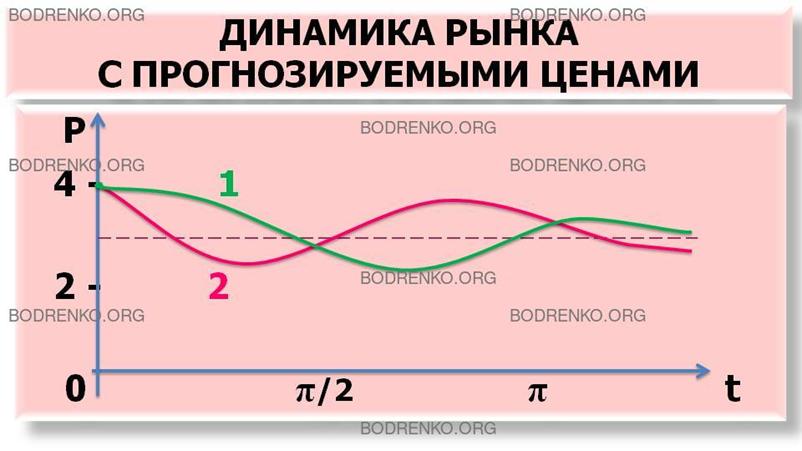
Рисунок
1.
РАЗДЕЛ 2. ГЛОБАЛЬНЫЕ ИМИТАЦИОННЫЕ МОДЕЛИ СИСТЕМНОЙ ДИНАМИКИ.
СЛЕДУЕТ ОТМЕТИТЬ НОВЫЙ КОНЦЕПТУАЛЬНЫЙ ПОДХОД – ПЕРЕХОД ОТ ПОНЯТИЯ
ЭКОНОМИЧЕСКОЙ СИСТЕМЫ К ПОНЯТИЮ ЭКОЛОГО-ЭКОНОМИЧЕСКОЙ СИСТЕМЫ.
В ЧЕМ СОСТОЯТ ОСНОВНЫЕ ПРЕДПОСЫЛКИ
НОВОГО ПОДХОДА?
Связь социального и экономического
впервые стала изучаться в рамках
классической политэкономии Кэне-Смита-Рикардо. Однако в конце XIX века, после
«революции Вальраса» и появления
«неоклассической» политэкономии, был выдвинут принцип «чистой экономии»
как науки. Основное внимание уделялось вопросам рынка, эволюции цен, движения
капитала и др. До сих пор вокруг этих проблем
сосредоточены основные усилия исследователей, они служат основой для
создания математических моделей и новых математических методов, создан разнообразный
и эффективный инструментарий,
позволяющий решать многочисленные и важные задачи. Однако
оказалось, что практическое решение задач оптимизации, эффективное на короткие
периоды времени в микроэкономическом
масштабе, приводит к существенным затратам в макроэкономическом плане в
силу возрастания эффекта накопления техногенного воздействия на окружающую среду. Масштабы
этого воздействия уже с середины XX
столетия стали приближаться к планетарным. В семидесятых годах XX
столетия становится очевидным, что
подобные подходы не могут обеспечить количественный анализ перспектив
экономического развития и оценку альтернативных вариантов целенаправленных международных действий, а
также решение сложных проблем взаимодействия человечества и окружающей среды.
Начало новым подходам положил Дж.
Форрестер; в его фундаментальной работе «Мировая динамика» с целью описания
глобального экологического процесса
впервые оказались «завязанными» в одну
математическую модель процессы развития экономики, демографии и загрязнения окружающей среды. Новый аспект
был развит в работах Д. Медоуза, Η. Η. Моисеева и других
исследователей. Важным результатом этой деятельности явилось осознание того,
что существуют глобальные проблемы кризисного характера, в которых экономика неотделима
от экологии. В условиях глобализации мировой экономики обеспечение жизнедеятельности мирового
сообщества в планетарных масштабах
становится главной задачей, носящей глобальный характер. Именно это обстоятельство обусловливает новый
концептуальный подход — переход от понятия экономической системы к понятию
эколого-экономической системы. Естественно, что в рамках такого подхода возникают новые специфические задачи и
модели.
КАКОВЫ ОСНОВНЫЕ АСПЕКТЫ ВЗАИМОДЕЙСТВИЯ
ЧЕЛОВЕКА И ОКРУЖАЮЩЕЙ СРЕДЫ?
В многовековом процессе эволюции
человека нагрузка на биосферу, как результат его производственной деятельности,
неуклонно возрастала. Еще на заре
цивилизации увеличение масштабов деятельности людей приводило к необратимым
изменениям в окружающей среде. Так, в Китае, например, огромные площади рисовых
полей совершенно изменили природные
ландшафты, вытеснили существовавшую
ранее фауну и флору и привели к новым климатическим условиям на больших
территориях. Известный российский ученый академик В. И. Вернадский в начале
30-х годов XX века ввел специальный термин «ноосфера», обозначающий среду
обитания сообщества людей, переделанную
под их нужды и существенно отличающуюся от природных условий. По сути дела к
ноосфере можно отнести все масштабные
изменения в природной обстановке, обусловленные производственной
активностью человечества: мегаполисы, сельское хозяйство, добычу природных
ресурсов, техногенные воздействия на биосферу при освоении новых территорий.
Ресурсная экосистема поддерживает
функционирование биосферы и цивилизации на нашей планете. Все ее ресурсы можно
условно разделить на возобновимые и
невозобновимые. Различие между ними
состоит в длительности периодов их восстановления; если для первой группы ресурсов период восстановления
сравнительно невелик (десятки лет), то для второй группы он превышает 1000 лет.
Масштабы деятельности людей стали уже
планетарными, что требует создания нового класса моделей развития с целью
выработки рекомендаций по координации
экономической активности государств для сохранения условий жизни на нашей
планете, а, следовательно, и успешного
развития мировой экономики. Здесь необходимо
рассмотреть основные аспекты проблемы.
ЭНЕРГЕТИЧЕСКИЙ АСПЕКТ.
Вместе с ростом производительности
труда, совершенствованием технологий и повышением квалификации
технологический уклад прошлых лет характеризовался все возрастающей энергоемкостью производства. В
прошлые века это было оправдано, поскольку происходил переход от
малопродуктивной системы производства к
высокопродуктивной системе. Основной вклад в развитие производительности труда
дала энергетика, именно она развивалась
опережающими темпами. Особенно наглядно это видно в развитии сельского
хозяйства; в середине XX в. средняя урожайность зерновых в развитых странах
возросла в три раза в результате роста энергозатрат на производство одной тонны
зерна почти на два порядка. Однако в
последнее время появились новые формы деятельности и технологии, требующие
значительно меньших затрат энергии:
микроэлектроника, биотехнологии, робототехника. Происходит совершенствование современных технологий
прежде всего в направлении уменьшения энергозатрат. Эта тенденция проявляется,
прежде всего, в том, что энергоемкие производства перемещаются из экономически
развитых стран в развивающиеся страны, иными словами, энергоемкость становится одной из важнейших
характеристик производства. Кроме того, в развивающихся странах значительно
дешевле рабочая сила, а также дешевле практически все: аренда, земля, электричество.
Поэтому туда и перемещают производства, а также для того, чтобы не тратить свои
энергоресурсы.
ПРОБЛЕМА ЗАМКНУТЫХ ТЕХНОЛОГИЙ.
Производственную деятельность людей можно рассматривать как глобальный
технологический процесс обеспечения
цивилизации всем необходимым. В последние
столетия эта технология стала принципиально незамкнутой: она не может существовать без использования
невозобновимых запасов земных недр. Имеет место не только истощение ископаемых
природных ресурсов, но и нехватка
возобновимых ресурсов, например, пресной воды. Именно поэтому во всех странах с
развитой экономикой предпринимаются
значительные усилия для создания и использования замкнутых технологий,
использующих возобновимые ресурсы, в том числе и энергетические.
АСПЕКТ ЗАГРЯЗНЕНИЙ.
Из экономически развитых стран идет
выталкивание в развивающиеся страны не только энергоемких технологий, но
и производств с большими загрязнениями биосферы. К ним относятся, например, добыча невозобновимых природных
ресурсов, черная металлургия, некоторые
виды химического производства. Именно с этим связан большой рост экспорта из
развивающихся стран сырья и металлов. Кроме, того, наблюдается тенденция
выталкивания и отходов высокотехнологичных производств передовых стран в
развивающиеся страны — например, вывоз радиоактивных отходов. Однако этот процесс представляется опасным, прежде всего,
тем, что он увеличивает разрыв между передовыми странами и развивающимися
странами не только в технологическом плане, но и в плане уровня жизни населения
и увеличения глобальной опасности разрушения биосферы.
ОСНОВНЫЕ ВИДЫ ЗАГРЯЗНЕНИЙ ОКРУЖАЮЩЕЙ
СРЕДЫ.
Можно сказать, что отходы производства
— это загрязнение окружающей среды при
незамкнутом производственном цикле. XX век охарактеризовался еще и ядерными
отходами с большим жизненным циклом. В природный круговорот оказались активно
включены инородные для природы компоненты — продукты антропогена, что приводит
к значительным и подчас необратимым изменениям в биосфере.
Число видов этих загрязнений велико, и
здесь мы укажем основные из них.
1. Прежде всего — это загрязнения
атмосферы. К ним относятся хлорфторуглеводороды, выбросы углекислого газа,
сернистых и азотнокислых соединений. Поднимаясь в верхние слои атмосферы Земли,
они вызывают процессы, отрицательно воздействующие на естественные природные
циклы биосферы. Наиболее опасным следует
признать разрушение озонового слоя в стратосфере, являющегося природным экраном от губительного
«жесткого» излучения Солнца.
2. Разработка и использование природных
ресурсов переводит потребляемые ресурсы
в потраченные (истощенные), которые
являются отходами производства. Наиболее массовые из них — это отходы черной и цветной металлургии и зола
ТЭЦ. Крупные по масштабам загрязнения
имеют место при разработке и использовании углеводородов. Отходы сельского хозяйства
представляют собой в основном
биозагрязнения и загрязнения от использования химикатов.
3. Сравнительно небольшие по объему, но
особо опасные по воздействию на
окружающую среду отходы, связанные с употреблением химических технологий:
выбросы тяжелых металлов, смесей,
растворов, излучений.
Указанные в п. 2 и п. 3 загрязнения
воздействуют на почвенный слой и источники воды (в том числе и подземные),
оказывая при больших масштабах губительное воздействие на окружающую среду.
ОРГАНИЗАЦИОННЫЙ АСПЕКТ.
Развитие технологий и научно-технический
прогресс требуют непрерывного совершенствования
организационных структур производственной деятельности, в том числе и на
международном уровне. Эти проблемы затрагивают взаимодействие человека и
биосферы в глобальном плане. Возникает необходимость учета социальных и
экологических факторов и долгосрочных
последствий принимаемых решении. Модели, позволяющие описать эти
процессы, фактически еще не созданы.
ЧТО ОЗНАЧАЕТ ТЕРМИН УСТОЙЧИВОЕ РАЗВИТИЕ?
Вопрос об устойчивом развитии впервые
был поставлен на международном уровне в
докладе Международной комиссии ООН
по окружающей среде и развитию в 1987 году.
Термин «устойчивое развитие» подразумевает следующие закономерности эволюции
цивилизации:
удовлетворение потребностей настоящего
времени, не ставящее под угрозу способность будущих поколений удовлетворять
свои потребности; учет социальных и
экологических факторов; учет
долгосрочных последствий принимаемых решений.
В экономическом плане это означает, что
при устойчивом развитии будут соблюдаться условия цивилизованного отношения
между настоящим и будущим:
-
на последующие поколения не возлагаются дополнительные
затраты;
-
отрицательные внешние эффекты между поколениями сводятся к
минимуму;
-
обеспечивается простое и/или расширенное
воспроизводство производственного
потенциала на перспективу;
-
обеспечивается жизнь человечества на проценты с
природного капитала.
Здесь следует отметить, что уменьшение
природоемкости является необходимым условием для перехода к устойчивому
развитию для отдельных стран и для
мировой экономики в целом. Движение по
траектории устойчивого развития подразумевает, прежде всего, снижение потребления природных ресурсов за
счет использования новых и
совершенствования функционирующих производственных технологий.
Целевыми ориентирами устойчивого
развития являются качество жизни,
уровень экономического развития, экологическая стабильность. Естественным
образом встает вопрос о мерах по обеспечению
устойчивого развития. Поэтому возникла концепция критического природного капитала как необходимых для жизни
природных благ, которые невозможно заменить искусственным путем. К ним
относятся: ландшафты, редкие виды флоры
и фауны, озоновый слой о верхней части земной атмосферы, глобальный климат и т.
д. Этот критический природный капитал необходимо сохранять при любых
сценариях экономического развития.
Остальная часть природного капитала может быть заменена искусственным путем —
прежде всего, имеются в виду
возобновимые и некоторая часть невозобновимых природных ресурсов (например, природные энергоресурсы
могут быть заменены на солнечную энергию, одного процента которой с избытком
хватило бы на обеспечение современной потребности человечества).
С учетом критического природного
капитала N* устойчивое развитие может быть дополнено ограничением на исчерпание
во времени этой величины.
ИЗ КАКИХ БЛОКОВ СОСТОИТ МОДЕЛИРОВАНИЕ И
АНАЛИЗ ЭКОЛОГО-ЭКОНОМИЧЕСКИХ СИСТЕМ?
Моделирование и анализ
эколого-экономических систем (ЭЭС) состоит из двух больших блоков: модели
загрязнения окружающей среды и модели использования ресурсов.

КАКИЕ МОДЕЛИ РАССМАТРИВАЮТСЯ В ПЕРВОМ
БЛОКЕ?
В случае глобальной модели ЭЭС в первом
блоке используются в основном модели загрязнения атмосферы; для моделей регионального плана используются также и
модели загрязнения водной среды и ландшафтов.

КАКИЕ МОДЕЛИ РАССМАТРИВАЮТСЯ ВО ВТОРОМ
БЛОКЕ?
Во втором
блоке рассматриваются три вида моделей использования
ресурсов:
-
неоклассическая экономическая модель (без учета ограниченности запасов ресурсов в ресурсной экосистеме и накапливания
отрицательных последствий их использования);
- природоохранная
модель (с необходимостью жестких ограничений на техногенную
деятельность и даже с концепцией «нулевого роста» — одним из основных требований движения «зеленых»);
- обобщенная
модель (учитывающая
условия устойчивого развития).

При построении модели основное внимание
уделяется структуре системы, которая
воспроизводила бы динамику протекающих в ней
процессов. В качестве своеобразных «кирпичиков» используются контуры
обратной связи; при этом параметры задания обратной связи могут быть заданы со
значительными погрешностями — это несущественно скажется на результатах
моделирования. Указанное свойство
системно-динамических моделей позволяет моделировать сложные системы при
наличии неполноты исходной информации или с использованием преимущественно
качественной информации.
КАКИЕ УСЛОВИЯ УЧИТЫВАЮТСЯ ПРИ
ИДЕНТИФИКАЦИИ СИСТЕМНО-ДИНАМИЧЕСКИХ МОДЕЛЕЙ?
Идентификация системно-динамических
моделей состоит из следующих основных
моментов:
-
модель должна выходить на все равновесные траектории,
присущие системе;
-
модель должна адекватно отражать время перехода от состояния
к состоянию (равновесные или квазистационарные состояния);
-
модель должна отражать характер динамики процессов, протекающих в системе — как установившихся,
так и переходных.

При соблюдении указанных условий
системно-динамический подход может служить удобным инструментом изучения
сложных систем в различных сферах экономики и находить оптимальные стратегии
при принятии решений.
РАЗДЕЛ
3. МОДЕЛИ СИСТЕМНОЙ ДИНАМИКИ «МИР-1»,
«МИР-2», «МИР-3».
Как мы уже отметили, основателем этого
направления является Дж. Форрестер. В
фундаментальной работе Дж. Форрестера «Мировая динамика» с целью описания
глобального экологического процесса
впервые оказались «завязанными» в одну математическую
модель процессы развития экономики, демографии и загрязнения окружающей среды. На основе
теории систем, аппарата дифференциальных уравнений и компьютерного моделирования Дж. Форрестер
разработал аппарат «системной динамики», позволяющий имитировать развитие
ситуаций. Им были созданы модели мировой
динамики «Мир-1» и «Мир-2» (1971—1972),
положившие начало глобальному моделированию. Впоследствии, в рамках
этого направления появились усовершенствованные модели и проекты.
Структура системно-динамических моделей ЭЭС включает в себя шесть секторов:
- население,
- капиталовложения (фонды),
- сельскохозяйственные фонды,

- ресурсы,
- загрязнение и
- управление.

Такая
структура была впервые предложена Дж. Форрестером и реализована в модели «Мир-2».
МАТЕМАТИЧЕСКИМ АППАРАТОМ СИСТЕМНОЙ
ДИНАМИКИ ЯВЛЯЮТСЯ ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА.
Модель «Мир-2» была построена с использованием 82 уравнений, описывающих взаимосвязи между элементами
системы. Первоначально построение и
анализ системно-динамических моделей носили скорее алгоритмический, нежели аналитический
характер. Сейчас, благодаря созданию объектно-ориентированных языков
программирования, стало возможным
создание больших моделей, включающих тысячи переменных, которые могут на
достаточно достоверном уровне описывать
динамику сложных систем.
В качестве иллюстрации можно привести
модель одного из шести указанных выше секторов — модель использования природных
ресурсов в ресурсном секторе модели
«Мир-3», разработанной в МГУ и
включающей в себя всего около 280 уравнений. Для каждого из
перечисленных выше секторов составляются системы
дифференциальных уравнений, причем все неизвестные функции «зацеплены» друг
с другом рядом соотношений.
В качестве примера результатов имитационного моделирования приведем результаты расчетов, проведенных по модели «Мир-2», разработанной еще Дж. Форрестером и Д. Медоузом. Здесь нам важна качественная интерпретация этих результатов, которая по-прежнему остается актуальной.
В качестве нулевого отсчета
времени был выбран 1900 год. Для разных сценариев (вариантов
переменных модели) рассчитывалась динамика восьми величин:
(1) – невозобновимые ресурсы;
(2) – производство продуктов питания;
(3) – численность населения;
(4) – выпуск промышленной продукции на душу
населения;

(5) – загрязнение окружающей среды;
(6) – общий темп смертности;
(7) – общий темп рождаемости;
(8) – производство услуг на душу населения в
год (в долларовом эквиваленте).

На рисунке 2 показаны соответствующие графики как результаты расчетов на 200 лет вперед в предположении о том, что никаких изменений в характере функционирования в глобальной ЭЭС не произойдет.
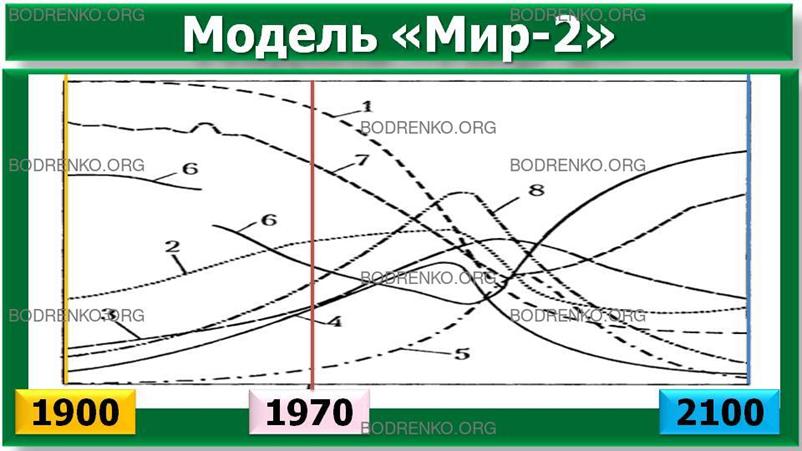
Рисунок 2. Графики как результаты расчетов по модели «Мир-2».
Следует сразу отметить, что масштабы кривых по вертикальной оси разные, однако здесь важна, прежде всего, тенденция и направленность процессов во времени. Результаты говорят о крахе системы в результате истощения невозобновимых природных ресурсов к 2100 году, хотя в 1970 году запас ресурсов еще около 95% от 1900 года. Рост капитала приводит к расходованию большей части ресурсов, а когда цены на них начинают расти, вследствие возрастания объема инвестиций в ресурсных отраслях объемы инвестиций в других отраслях падают. Наступает крах промышленной производственной базы, что обусловливает деградацию сельскохозяйственного производства и производства услуг.
Вследствие инерционного роста населения социальная обстановка ухудшается — увеличивается темп смертности из-за недостатка питания и медицинских услуг. Переход к стадии деградации приходится примерно на первую половину XXI века, после пика развития. Точное время наступления этих событий не является значимым из-за высокого уровня агрегирования переменных модели, однако значение имеет тот факт, что рост прекращается задолго до 2100 года.
Все сценарии без контроля над загрязнением дают пессимистические прогнозы для жизнедеятельности человека: даже при «неограниченных» ресурсах общий темп смертности к 2100 году нарастает вследствие быстрого роста загрязнения окружающей среды, падает численность населения, хотя выпуск продукции и услуг на душу населения растет.
При реализации в модели достижений
научно-технического прогресса,
позволяющих избежать истощения ресурсов и быстрого загрязнения окружающей среды (полагалось, что
с 1975 года загрязнения от всех источников снижаются в 4 раза), но в условиях
прежних стратегий использования ресурсов
результаты прогноза являются более
оптимистичными (рисунок 3).
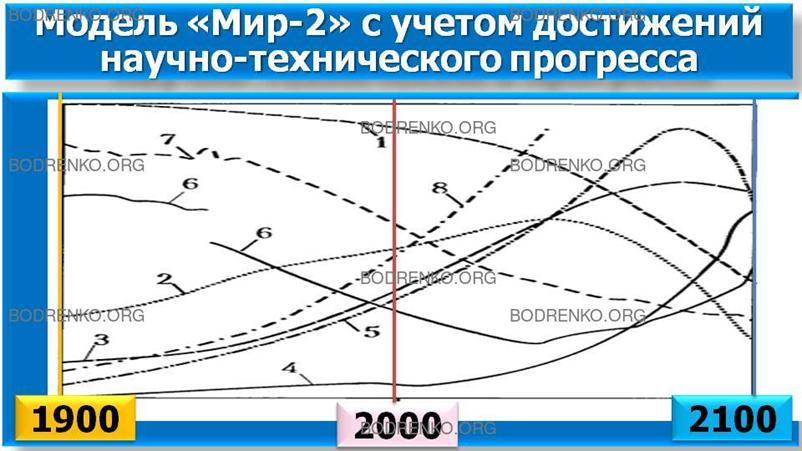
Рисунок 3. Графики как результаты расчетов по модели «Мир-2» с учетом достижений научно-технического прогресса.
Все пики смещаются к 2100 году, причем
общий уровень загрязнения окружающей среды возрастает. При достижении предела
орошаемых земель производство продуктов питания падает, и рост промышленной
продукции замедляется из-за оттока капитала в сектор производства продуктов
питания.
ЧТО ПРЕДСТАВЛЯЕТ СОБОЙ
«СТАБИЛИЗИРОВАННАЯ МОДЕЛЬ МИР-1»?
В так называемой «Стабилизированной
модели Мира-1» к ограничивающим
стратегиям добавлены также стратегии научно-технического прогресса, включающие
в себя:
- вторичную переработку ресурсов,
- контроль над окружающей средой,
- увеличение срока службы капитала всех
видов,
- восстановление утраченных из
сельскохозяйственного оборота земель.
Аспект управления состоит в том, что
усилен акцент на производство услуг и продуктов питания, остановлен
прирост населения, инвестиции в промышленный
капитал равны его амортизации. Результаты этого сценария показаны на рисунке 4.
При снижении ресурсов примерно на треть все основные показатели стабилизируются на уровне примерно 2000 года.
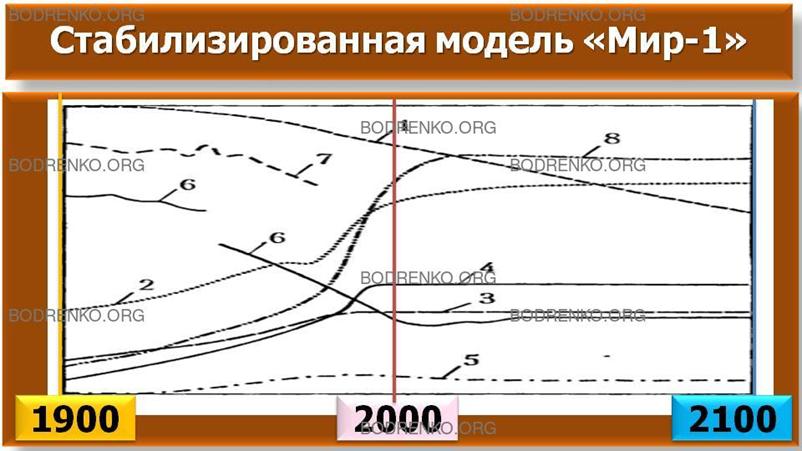
Рисунок 4. Графики как расчеты по модели «Стабилизированная модель Мир-1».
Анализируя системно-динамический подход
в целом, необходимо отметить следующие
аспекты прогнозирования.
1. Все сценарии прогноза нужно
воспринимать, прежде всего, с
качественной стороны, что само по себе уже крайне важно.
2. Прогнозы на длительные сроки
заведомо неустойчивы, поскольку они представляют собой экстраполирование
современных экономических и
технологических возможностей на далекое будущее.
3. Как известно, мультипликатор
научно-технического прогресса является
экспоненциально растущим во времени. В силу этого высокие технологии
обновляются всего за несколько лет. Следовательно, мы сейчас стоим на
пороге разработки и внедрения
принципиально новых ресурсосберегающих, ресурсозаменяющих и замкнутых
технологий производства. Разумеется,
процесс использования таких технологий будет далеко не равномерным по разным
странам и регионам.
4. По-видимому, в ближайшем будущем
имеет смысл проводить прогноз с
использованием системно-динамических моделей с
обновленными программными модулями, отражающими новые технологии, причем в силу возрастающей
интенсивности темпов развития этих технологий вряд ли имеет смысл
прогнозирование на период более 50 лет.
5. Ввиду активизации процессов
глобализации мировой экономики следует уделять большее внимание аспекту
координированного управления экономическими процессами и техногенным влиянием человека на биосферу и окружающую
среду с целью выбора оптимальных
стратегий эволюции эколого-экономических систем.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Занг
В.-Б. Синергетическая экономика. Время и перемены в нелинейной экономической
теории. Пер. с англ. – М.: Мир, 1999. - 335 с.: ил.
[2] Колемаев В.А. Математическая экономика: Учебник для вузов.
— 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2002. - 399 с.

[3] Красс М.С., Чупрынов Б.П. Основы
математики и ее приложения в экономическом образовании: Учебник. 4-е изд.,
испр. – М.: Дело, 2003. – 688 с.
[4] Фомин Г. П.
Математические методы и модели в
коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и
статистика, 2005. — 616 с: ил.
[5] Шикин Е.
В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб.
пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический
университетский учебник»).
