Хранилища данных. Многомерные хранилища данных. Многомерная модель данных. Многомерные кубы: определение и свойства. Хранение и эффективный расчет OLAP-кубов. Хранилища данных и системы бизнес-аналитики. Модели и методы добычи данных. Архитектура хранилищ данных.
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Хранилища данных
Лекция 2
Тема лекции: «Многомерные
хранилища данных»

1.
Многомерная модель данных.
2.
Многомерные кубы: определение и свойства.
3.
Хранение и
эффективный расчет OLAP-кубов.

1.
МНОГОМЕРНАЯ МОДЕЛЬ ДАННЫХ.
Тема создания и использования хранилищ данных
(ХД) сегодня становится все более популярной как в публикациях
специализированных СМИ и частных беседах специалистов, так и в коммерческих
предложениях компаний. Это заставляет задумываться не только об организационных
и технических аспектах проблемы, или о вопросе «КАК?», но и требует ответа на
вопрос «ЗАЧЕМ?» С другой стороны, когда мы говорим о технологиях, которые
рождены какой-то одной компанией, наше видение проблем ограничено возможностями
рассматриваемых продуктов. Ценным является понимание границ возможностей
конкретных продуктов и технологий.
Попытаемся ответить на вопросы, ЗАЧЕМ
создавать хранилища данных, и КАК это делать. И очертим границы, в которых
имеет смысл использовать эти технологии.
Давайте обратим внимание на
происхождение задачи создания хранилищ данных. Автоматизация или
компьютеризация предприятий, как правило, происходит исторически и «снизу
вверх» (за исключением случаев полной реорганизации, которые имеют достаточно
мало удачных финалов). Определенные подразделения, которые заняты массовыми
операциями по обработке данных (выписка счетов, учет производства, складской
учет, работа с поставщиками и пр.), подвергаются процессу целевой
автоматизации. Это означает, что массовые задачи будут производиться с помощью
компьютеров, которые заменят работу с бумажными носителями информации
(документы, бланки) на режим, в котором действия отражаются в базах данных, или
(что чаще всего и происходит) информация будет дублироваться как на бумажных
носителях, так и в базах данных.
В силу того, что компьютеризации (или
отражению в базе данных) подвергается каждый раз небольшой фрагмент процессов
предприятия, и это происходит не всегда согласованно, большинство баз данных
плохо согласованы друг с другом. Фраза «плохо согласованы» означает, что в
различных базах данных одинаковые объекты реального мира могут быть отражены по-разному
(например, Иванов И. И. при начислении заработной платы и Иванов Иван Иванович
при получении материальных ценностей в подотчет). Эта проблема может решаться
введением централизованных справочников и словарей уровня предприятия, что само
по себе является нетривиальным техническим процессом.
Над целевыми базами данных исполняются
целевые транзакции (например, занесение в таблицу записи с параметрами
выписанного счета, оприходованной фактуры или любого другого факта). Такие системы обычно называют системами
оперативной обработки транзакций, или OLTP-системами. Целевые транзакции
изменяют состояние баз данных и приводят их в соответствие текущему состоянию
того фрагмента реального мира, который моделирует база данных. Таким образом,
основным назначением целевых баз данных является обработка транзакций.
Другой большой пласт задач над целевыми
базами данных связан с созданием отчетов за определенный период существования
базы данных. Форма этих отчетов может незначительно меняться и, как правило,
определяется внешними правилами (правила ведения бухгалтерского учета) и
внутренними правилами (должностные инструкции, приказы и распоряжения), в
рамках которых существует предприятие.
Создаваемые в процессе такой
автоматизации базы данных, как правило, максимально оптимизированы для быстрого
выполнения необходимых транзакций, рассчитаны на производство небольшого
количества отчетов и хранят данные за небольшой временной период.
Если постепенно (или единовременно)
автоматизации подверглись все бизнес-процессы предприятия, то ситуация обычно
будет отличаться лишь тем, что уже началось решение проблемы плохого
согласования данных, или эта проблема уже решена. В тот момент, когда мы
наблюдаем подобную ситуацию, можно задать себе вопросы: «Какие процессы
подверглись автоматизации? Работа какого
персонала была автоматизирована и облегчена?» Ответы на эти вопросы достаточно
очевидны: автоматизирована работа исполнителей, которые выполняют типовые
процедуры. Автоматизация почти не затронула управленцев – персонал,
ответственный за принятие решений.
Создание «хранилищ данных» (а также, «витрин
данных») позволяет произвести следующий этап автоматизации деятельности
предприятия – создать средства поддержки принятия решений. Основным отличием
деятельности по принятию решений от исполнительской деятельности, с точки
зрения используемых данных, является потребность во всестороннем видении
процессов во всем многообразии параметров, от которых они зависят, за различные
временные промежутки. Можно сказать, что исполнители работают с данными о
происходящих процессах, тогда как управленцам необходима информация для
принятия решений. Этот факт определяет и используемые данные. Для создания систем
поддержки принятия решений необходима полная, непротиворечивая, информация за
различные временные промежутки, которая может быть, как обобщена
(просуммирована или агрегирована другим способом), так и детализирована. Именно
эти требования являются определяющими при создании хранилищ данных как
базиса для создания систем поддержки принятия решений.
ДЛЯ ПРОЦЕССА ПРИНЯТИЯ РЕШЕНИЙ СОЗДАЮТСЯ
СРЕДСТВА ИЗ ТРЕХ БОЛЬШИХ ГРУПП:
-
средства
генерации отчетов (Reporting tools);
-
средства
оперативного анализа (OLAP tools);
-
средства
добычи данных (Data Mining tools);

Средства генерации отчетов
предназначены для получения данных в виде таблиц и диаграмм (иногда
используются и другие формы представления данных, например, диаграммы,
нанесенные на геокарты, и пр.). Этот класс средств позволяет управленцам
контролировать происходящие процессы, имея некоторое количество фиксированных
взглядов на показатели этих процессов.
Средства оперативного анализа
нацелены на проверку гипотез, они позволяют найти данные, которые подтверждают
или опровергают сформулированные управленческие гипотезы. Гипотезы могут
формулироваться как очень определенно (падение прибыли произошло из-за
повышения себестоимости), так и более нечетко (есть параметры деятельности,
которые наиболее сильно отличают подразделение, принесшее наибольшую прибыль),
в результате положительного ответа на такой вопрос можно также узнать, какое
это подразделение, и какие параметры его деятельности наиболее сильно
отличаются. Эта информация позволяет управленцам изменять процессы предприятия
для достижения определенных целей.
Средства добычи данных
предназначены для создания гипотез на основе существующих данных. Этот класс
средств наиболее сильно зависит от предметной области и структуры исходных
данных. Однако наличие подобных средств просто необходимо в случае больших
объемов данных и большого количества параметров, от которых эти данные зависят,
т. к. они позволяют обнаружить (или, другими словами, сделать видимыми,
отображаемыми) факты и тенденции, которые совершенно неочевидны при обычном
просмотре огромных массивов данных.
Специфические формы использования
данных (в отличие от обработки транзакций над целевыми базами данных) порождают
соответствующие требования к используемым моделям хранения и представления
данных. Если целевые базы данных были максимально оптимизированы для
представления фрагмента всех данных, которые используются на предприятии, и для
выполнения целевых транзакций с максимальной производительностью, то для хранилищ
данных характерно представление информации обо всех взаимосвязанных процессах
предприятия. С другой стороны, хранилища данных и целевые базы данных
существенно различаются типами запросов к ним. Целевые транзакции сочетают в
себе не только запросы для просмотра данных, но и процедуры модификации данных
и занесения новых данных. В случае хранилищ данных мы будем иметь дело, в
первую очередь, с получением данных, основная масса запросов к хранилищам
данных — это запросы по выборке данных.
Наиболее распространенной моделью для
хранилищ данных является пространственная модель или модель многомерных кубов данных.
Пространственная (или многомерная) модель данных
позволяет хранить значения измеряемых
параметров или мер в едином объекте данных с определяющими параметрами или аргументами;
ПРИМЕР.
Примерами измеряемых
параметров (мер) являются: сумма на
счете, оборот, сумма продажи, количество товара, объем выполненной услуги.
Далее определяющие параметры (аргументы) мы будем называть
измерениями.
ПРИМЕР.
Примерами измерений являются: номер
счета, дата проводки, номер накладной, кто плательщик, наименование и тип
товара, наименование услуги и пр.
Стоит отметить, что данные для хранилищ
получаются из целевых оперативных баз данных. Учитывая, что хранилища данных
содержат в едином объекте информацию о различных сторонах процессов, которые
могли отражаться в различных целевых базах данных, необходим процесс
объединения данных из различных источников, или процесс консолидации.
Большинство измерений (параметров, от которых зависят меры)
неоднородно.
ПРИМЕР.
Например, если мы говорим о наименовании товара, то также
можно говорить и о некоторой товарной группе, типе товара.
Таким образом, измерение «товар» может иметь иерархию наименовании. Например, тип товара -> товарная группа ->
наименование товара.
Причем, при анализе данных и принятии решения часто
необходимо работать не с числовыми величинами, специфичными для конкретного
товара; бывает достаточно детализации уровня товарной группы или даже типа
товара. Для обеспечения быстрого доступа к этой просуммированной информации
хранилища данных, как правило, содержат эту информацию уже вычисленной. Процесс
вычисления подобных сумм называется агрегация, а сами величины — агрегатами.
В многомерных хранилищах данных
содержатся агрегатные данные различной степени подробности, например, объемы
продаж по дням, месяцам, годам, по категориям товаров и т.п.
Цель хранения агрегатных данных —
сократить время выполнения запросов, поскольку в большинстве случаев для
анализа и прогнозов интересны не детальные, а суммарные данные. Поэтому при
создании многомерной базы данных всегда вычисляются и сохраняются некоторые
агрегатные данные.
Отметим, что сохранение всех агрегатных
данных не всегда оправданно. Дело в том, что при добавлении новых измерений объем
данных, составляющих куб, растет экспоненциально (иногда говорят о «взрывном
росте» объема данных). Если говорить более точно, степень роста объема
агрегатных данных зависит от количества измерений куба и членов измерений на
различных уровнях иерархий этих измерений. Для решения проблемы «взрывного
роста» применяются разнообразные схемы, позволяющие при вычислении далеко не
всех возможных агрегатных данных достичь приемлемой скорости выполнения
запросов.
Для создания хранилищ данных очень
часто используются обычные реляционные базы данных. В этом случае схему базы
данных организуют как звезду (Star Flake) или снежинку (Snow Flake).
Типичная структура хранилища данных
существенно отличается от структуры обычной реляционной СУБД – как правило, она
денормализована; основными составляющими
структуры хранилищ данных являются таблица
фактов (fact table) и таблицы
измерений (dimension tables).
Например, при организации схемы базы
данных в виде звезды в центре находится таблица фактов или таблица, описывающая
меры, а с ней связаны таблицы параметров или измерений.
Как
отмечалось в лекции 1, в концепции ХД нет постановки вопросов, связанных с
организацией эффективного анализа данных и предоставления доступа к ним. Эти
задачи решаются подсистемами анализа. Попробуем разобраться, какой способ
работы с данными наиболее подходит пользователю СППР – аналитику.
В
процессе принятия решений пользователь генерирует некоторые гипотезы.
Для
превращения этих гипотез в законченные решения они должны быть проверены. Проверка
гипотез осуществляется на основании информации об анализируемой предметной
области. Как правило, наиболее удобным способом представления такой информации
для человека является зависимость между некоторыми параметрами. Например,
зависимость объемов продаж от региона, времени, категории товара и т. п. Другим
примером может служить зависимость количества выздоравливающих пациентов от
применяемых средств лечения, возраста и т. п.
В
процессе анализа данных, поиска решений, часто возникает необходимость в
построении зависимостей между различными параметрами. Кроме того, число таких
параметров может варьироваться в широких пределах. Как уже отмечалось,
традиционные средства анализа, оперирующие данными, которые представлены в виде
таблиц реляционной БД, не могут в полной мере удовлетворять таким требованиям.
В
1993 году Э. Ф. Кодд – основоположник реляционной модели БД, рассмотрел ее
недостатки, указав в первую очередь на невозможность «объединять, просматривать
и анализировать данные с точки зрения множественности измерений, т. е. самым
понятным для аналитиков способом».
Далее
под измерением мы будем понимать последовательность
значений одного из анализируемых параметров.
ПРИМЕР.
Например, для параметра «время» измерение – это последовательность календарных дней.
Для параметра «регион» измерение – это, например, список городов.
Множественность
измерений предполагает представление данных в виде многомерной модели. По
измерениям в многомерной модели откладывают параметры, относящиеся к
анализируемой предметной области.
По
Кодду, многомерное концептуальное
представление (multi-dimensional conceptual view) – это множественная перспектива, состоящая из
нескольких независимых измерений, вдоль которых могут быть проанализированы
определенные совокупности данных. Одновременный анализ по нескольким измерениям
определяется как многомерный анализ.
Каждое
измерение может быть представлено в виде иерархической структуры.
ПРИМЕР.
Например, измерение «Исполнитель» может
иметь следующие иерархические уровни: «предприятие – подразделение – отдел – служащий».
Более
того, некоторые измерения могут иметь несколько видов иерархического
представления.
ПРИМЕР.
Например, измерение «время» может включать
две иерархии со следующими уровнями:
«год — квартал — месяц — день» и «неделя —
день».
На пересечениях осей измерений (Dimensions) располагаются данные,
количественно характеризующие анализируемые факты, – меры (Measures). Это
могут быть объемы продаж, выраженные в единицах продукции или в денежном
выражении, остатки на складе, издержки и т. п.
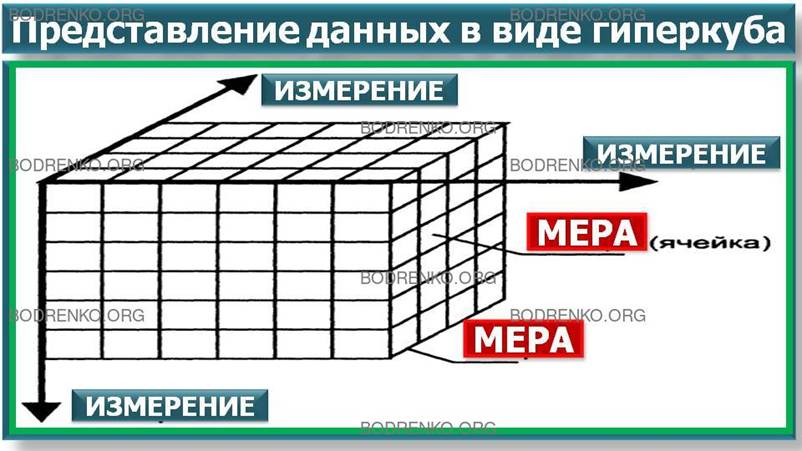
Рисунок 1. Представление данных в виде гиперкуба.
Таким
образом, многомерную модель данных можно представить как гиперкуб (рисунок 1)
(конечно, название не очень удачно, поскольку под кубом OLAP-системы обычно
понимают фигуру с равными ребрами, что в данном случае далеко не так). Ребрами
такого гиперкуба являются измерения, а ячейками – меры.
Над
таким гиперкубом могут выполняться следующие ОПЕРАЦИИ:
-
Срез (Slice)
(рисунок 2). Формируется подмножество многомерного массива данных,
соответствующее единственному значению одного или нескольких элементов
измерений, не входящих в это подмножество.
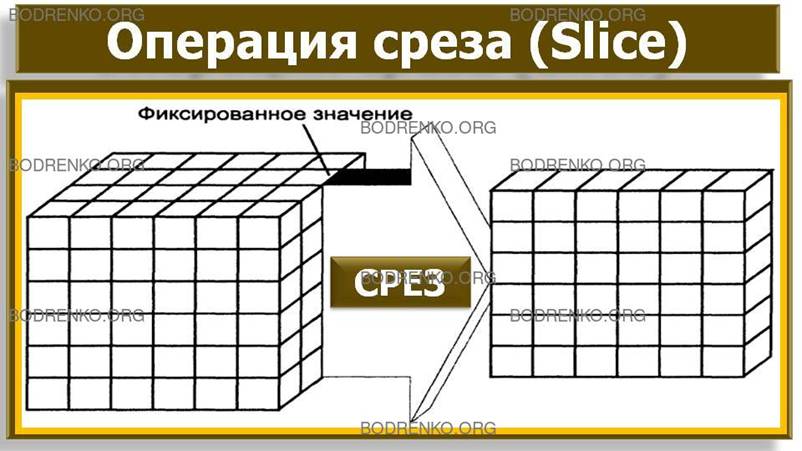
Рисунок 2. Операция среза.
Например,
при выборе элемента «Факт» измерения «Сценарий» срез данных представляет собой
подкуб, в который входят все остальные измерения.
Данные,
которые не вошли в сформированный срез, связаны с теми элементами измерения «Сценарий»,
которые не были указаны в качестве определяющих (например, «План», «Отклонение»,
«Прогноз» и т. п.).
Если
рассматривать термин «срез» с позиции конечного пользователя, то наиболее часто
его роль играет двумерная проекция куба.
- Вращение (Rotate) (рисунок
3). Изменение расположения измерений,
представленных в отчете или на отображаемой странице. Например, операция вращения может заключаться
в перестановке местами строк и столбцов таблицы или перемещении интересующих
измерений в столбцы или строки создаваемого отчета, что позволяет придавать ему
желаемый вид.
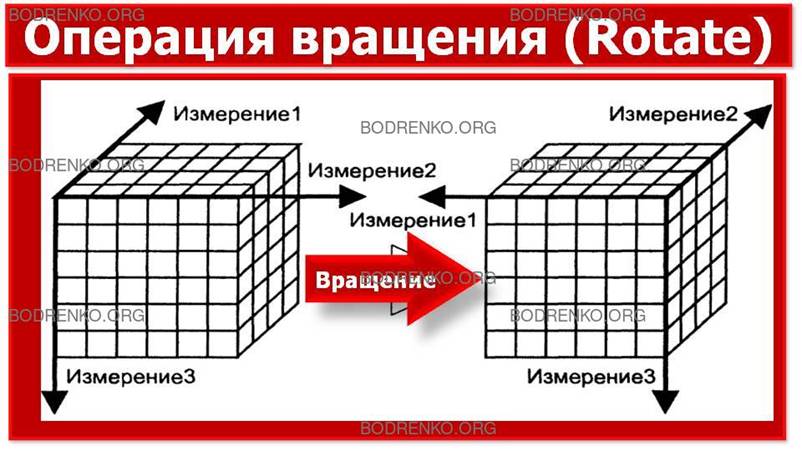
Рисунок 3. Операция вращения.
Кроме
того, вращением куба данных является перемещение внетабличных измерений на
место измерений, представленных на отображаемой странице, и, наоборот (при этом
внетабличное измерение становится новым измерением строки или измерением
столбца).
ПРИМЕР.
В качестве примера для первого случая может
служить такой отчет, для которого элементы измерения «Время» располагаются
поперек экрана (являются заголовками столбцов таблицы), а элементы измерения «Продукция»
— вдоль экрана (являются заголовками строк таблицы). После применения операции
вращения отчет будет иметь следующий вид: элементы измерения «Продукция» будут
расположены по горизонтали, а элементы измерения «Время» – по вертикали.
ПРИМЕР.
Примером второго случая может служить
преобразование отчета с измерениями «Меры»
и «Продукция», расположенными по вертикали, и измерением «Время», расположенным
по горизонтали, в отчет, у которого измерение «Меры» располагается по
вертикали, а измерения «Время» и «Продукция» – по горизонтали. При этом элементы измерения «Время»
располагаются над элементами измерения «Продукция».
ПРИМЕР.
Для третьего случая применения операции
вращения можно привести пример преобразования отчета с расположенным по
горизонтали измерением «Время» и измерением «Продукция», расположенным по
вертикали, в отчет, у которого по горизонтали представлено измерение «Время», а
по вертикали — измерение «География» (синоним: Pivot).
-
Консолидация (Drill Up) и детализация (Drill
Down) (рисунок 4). Операции, которые определяют переход вверх по
направлению от детального (down) представления данных к агрегированному (up) и
наоборот, соответственно. Направление детализации (обобщения) может быть задано
как по иерархии отдельных измерений, так и согласно прочим отношениям,
установленным в рамках измерений или между измерениями.
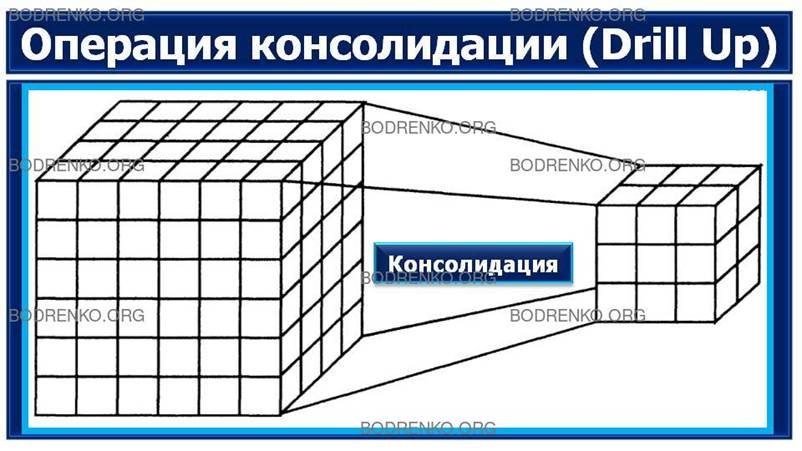
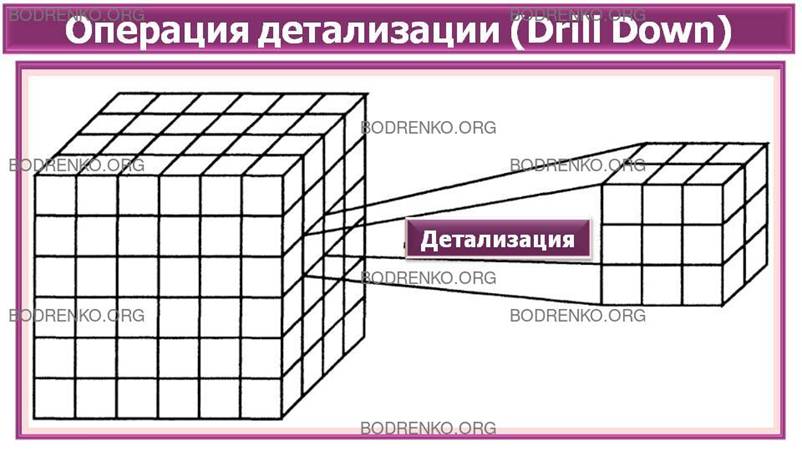
Рисунок 4. Операции консолидации и детализации.
ПРИМЕР.
Например, если при анализе данных об
объемах продаж в Северной Америке выполнить операцию Drill Down для измерения «Регион»,
то на экране будут отображены такие его элементы, как «Канада», «Восточные
Штаты Америки» и «Западные Штаты Америки». В результате дальнейшей детализации
элемента «Канада» будут отображены элементы «Торонто», «Ванкувер», «Монреаль» и
т. д.
2. МНОГОМЕРНЫЕ КУБЫ, ОПРЕДЕЛЕНИЕ И СВОЙСТВА.
Итак, основными понятиями многомерной
модели данных:
Мера (Measures) (показатель) - это величина (обычно
числового типа), которая собственно и является предметом анализа. Это,
например, объём продаж некоторого товара, или выручка от продаж товара. Один
OLAP-куб может обладать одним или несколькими показателями.
Измерение (dimension)
- это множество объектов одного или нескольких типов, организованных в виде
иерархической структуры и обеспечивающих информационный контекст числового
показателя.
Измерение принято визуализировать в виде ребра многомерного
куба.
Объекты, совокупность которых и
образует измерение, называются членами
измерений (members).
Члены измерений визуализируют как точки или участки,
откладываемые на осях гиперкуба.
ПРИМЕР.
Например,
временное измерение: Дни, Месяцы, Кварталы, Годы - наиболее часто используемые
в анализе, могут содержать следующие члены: 21 августа 2015 года, август 2015
года, 3-й квартал 2015 года и 2015 год.
Как уже было сказано, объекты в
измерениях могут быть различного типа, например «производители» – «марки
автомобиля» или «годы» - «кварталы». Эти объекты должны быть организованы в
иерархическую структуру так, чтобы объекты одного типа принадлежали только
одному уровню иерархии.
Ячейка (cell) -
атомарная структура куба, соответствующая конкретному значению некоторого
показателя (меры).
Ячейки при визуализации располагаются внутри куба и здесь же
принято отображать соответствующее значение показателя (меры).
Измерения играют роль индексов,
используемых для идентификации значений показателей, находящихся в ячейках
гиперкуба. Комбинация членов различных измерений играют роль координат, которые
определяют значение определенного показателя (рисунок 1).
Поскольку для куба может быть
определено несколько показателей, то комбинация членов всех измерения будет
определять несколько ячеек со значениями каждого из показателей. Поэтому для
однозначной идентификации ячейки необходимо указать комбинацию членов всех
измерений и показатель. На рисунке 1 изображен куб с тремя измерениями.
Заметим, что, в отличие от измерений,
не все значения показателей должны иметь и имеют реальные значения. Например,
Менеджер Петров в 2014 году мог еще не работать в фирме, и в этом случае все
значения Показателя «Объем продаж» за этот год 2014 год будут иметь
неопределенные, «пустые» значения (для Менеджера Петрова).
ИЕРАРХИИ В ИЗМЕРЕНИЯХ необходимы для
возможности агрегации и детализации значений показателей согласно иерархической
структуре.
Поддерживаются следующие типы иерархий.
Сбалансированные (balanced)
– иерархии, в которых число уровней определено её структурой и неизменно, и
каждая ветвь иерархического дерева содержит объекты каждого из уровней. Каждому
производителю автомобилей может соответствовать несколько марок автомобилей, а
каждой марке — несколько моделей автомобилей, поэтому можно говорить о
трёхуровневой иерархии этих объектов. В этом случае на первом уровне иерархии
располагаются производители, на втором — марки, а на третьем — модели.
Как нетрудно понять, что для
формирования сбалансированной иерархии необходимо наличие связи «один-ко-многим»
между объектами менее детального уровня по отношению к объектам более
детального уровня. В принципе каждый уровень сбалансированной иерархии можно
представить как отдельное простое измерение, но тогда эти измерения окажутся
зависимыми, в значит неизбежно повышение разреженности куба.
Несбалансированные (unbalanced) –
иерархии, в которых число уровней может быть изменено, и каждая ветвь
иерархического дерева может содержать объекты, принадлежащие не всем уровням,
только нескольким первым. Необходимо заметить, что все объекты
несбалансированной иерархии принадлежат одному типу. Типичный пример
несбалансированной иерархии — иерархия типа «начальник—подчиненный», где все
объекты имеют один и тот же тип – «Сотрудник».
Неровные (ragged) – иерархии, в которых число
уровней определено её структурой и постоянно, однако в отличие от
сбалансированной иерархии некоторые ветви иерархического дерева могут не
содержать объекты какого-либо уровня. Иерархии такого вида содержат такие
члены, логические «родители» которых не находятся на непосредственно
вышестоящем уровне. Типичным примером является географическая иерархия, в
которой есть уровни «Страны», «Штаты» и «Города», но при этом в наборе данных
имеются страны, не имеющие штатов или регионов между уровнями «Страны» и «Города».
Несбалансированные и неровные иерархии
встречаются достаточно редко по сравнению со сбалансированными иерархиями.
По
другой классификации (см.: [3]) все иерархии можно разбить на 2 типа.
Основой разбиения будет служить расстояние от корня до листьев. В случае, если
расстояния одинаковы для всех листов, то иерархии называются уровневыми
(leveled) (см. рисунок 5), иначе – «неровными» (ragged).
ПРИМЕРЫ ТИПОВ ИЕРАРХИЙ.
Уровневые:
«день-месяц-год»; «улица — город — страна».
«Неровные»:
Организационная диаграмма, различная группировка
продуктов.
Важным свойством уровневых иерархий
является возможное наличие частичного порядка внутри каждого уровня иерархии,
например, возможность сравнения месяцев по старшинству или городов по
географическому положению. В большинстве современных средств (алгоритмов)
данным свойством пренебрегают, удаляя, тем самым, потенциально полезные связи
модели.
Иерархии могут быть
сбалансированными (balanced), как, например, иерархия, представленная на рисунке
5, а также иерархии, основанные на данных типа «дата—время», и
несбалансированными (unbalanced).
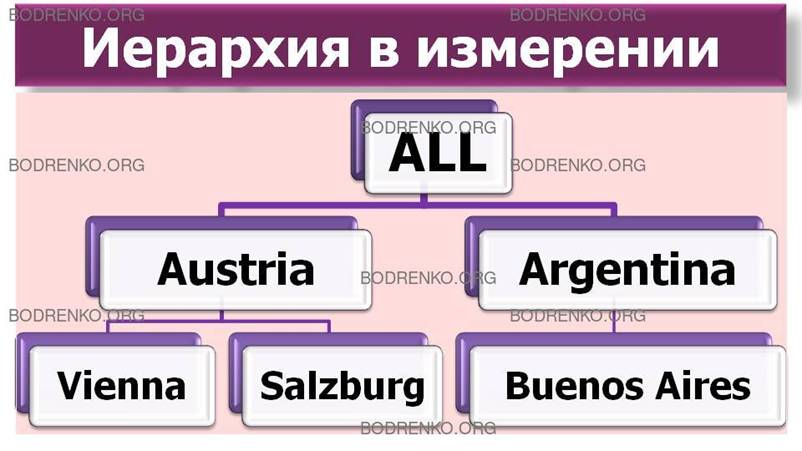
Рисунок 5. Иерархия в измерении, связанном с
географическим положением клиентов.
«Неровные» иерархии занимают промежуточное положение между сбалансированными и несбалансированными (они обозначаются термином ragged — «неровный»). Обычно они содержат такие члены, логические «родители» которых находятся не на непосредственно вышестоящем уровне. Например, в географической иерархии есть уровни Country, City и State, но при этом в наборе данных имеются страны, не имеющие штатов или регионов между уровнями Country и City (рисунок 6).
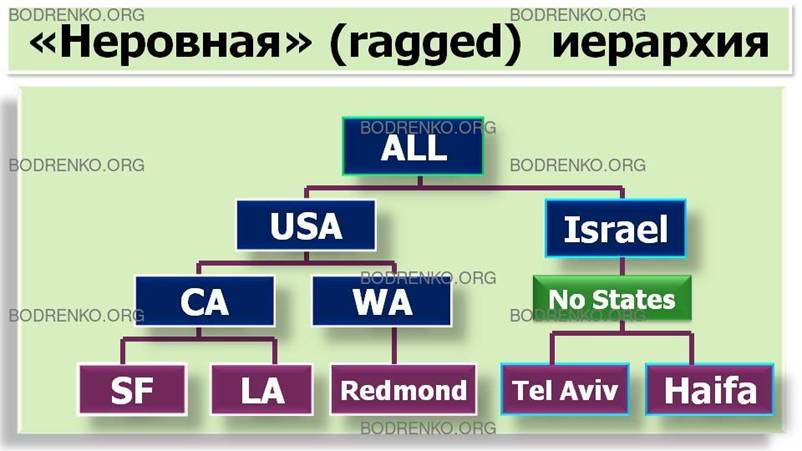
Рисунок
6. «Неровная» иерархия.
Агрегатами называют агрегированные по
определенным условиям исходные значения показателей (мер).
Обычно под агрегацией понимается любая
процедура формирования меньшего количества значений (агрегатов) на основании
большего количества исходных значений. В дальнейшем под терминами агрегирование
и агрегация будем понимать исключительно процесс суммирования данных.
Заблаговременное формирование и
сохранение агрегатов с целью уменьшения времени отклика на пользовательский
запрос является основным свойством систем поддержки оперативного анализа.
Рассмотрим базовую (фактическую)
таблицу, на основе которой мы будем
строить OLAP- куб. Множество атрибутов r условно
делятся на 2 группы:
1. Набор измерений (категорий,
локаторов), которые служат критериями для анализа и определяют многомерное
пространство OLAP-куба. За счет фиксации значений измерений получаются срезы
(гиперплоскости) куба. Каждый срез представляет собой запрос к данным,
включающий агрегации.
2. Набор
мер – функции, которые каждой точке
пространства ставят в соответствие данные.
Из атрибутов создаются измерения,
содержащие проекцию r по атрибуту, с
введенной иерархией.
ПРИМЕР.
Например, для таблицы, содержащей
фактические данные по продажам магазина, возможно измерение «Время», содержащее
иерархию вида «Год-Месяц-Неделя-День».
Куб представляет собой декартово
произведение измерений, где для каждого элемента произведения проставлен набор
мер (существует проблема хранения неопределенных значений).
В кубе существуют отношения обобщения и
специализации (roll-up/drill-down) по иерархиям измерений.
Ячейка высокого уровня иерархии может «спускаться»
(drill-down) к ячейке низкого уровня.
ПРИМЕР.
Например, ячейка (R1, ALL,
весна) может «спуститься» (drill-down) к ячейке (R1, книги, весна).
И, наоборот, «подняться» (roll-up) от ячейки (R1, книги, весна) к (R1, ALL, весна) по измерению «Продукты».
2.1.
Измерения.
Измерения куба
— набор доменов, по которым создается многомерное пространство.
Важной особенностью OLAP-моделей
является разделение измерений на локаторы (задающие точки) и
меры (задающие значение).
Данное разделение может носить как
условный, так и жесткий характер. В случае условного разделения измерения можно
«разворачивать» как данные и как аналитику, создавая новую аналитику куба по
продажам – «количество продаж». Таким
образом, возрастает гибкость моделей и уровень абстракции. Однако данный
подход, несмотря на свою привлекательность, сложен в реализации (для примера
отметим необходимость создания оптимальных алгоритмов хранения абстрактных
типов данных). Теоретически, вкупе с моделированием решеток кубов логикой
предикатов первого порядка, абстрагирование понятия «измерение» дает очень
интересные результаты.
Для описания значений данных в ячейках, используется термин summary (в общем случае в одном кубе их может быть несколько).
Для обозначения исходных данных, на основе которых они вычисляются, используется термин measure.
Для обозначения параметров запросов используется термин dimension (переводимый на русский язык обычно как «измерение», когда речь идет об OLAP-кубах, и как «размерность», когда речь идет о хранилищах данных).
Значения, откладываемые на осях, называются членами измерений (members).
Говоря об измерениях, следует упомянуть о том, что значения, наносимые на оси, могут иметь различные уровни детализации. Например, нас может интересовать суммарная стоимость заказов, сделанных клиентами в разных странах, либо суммарная стоимость заказов, сделанных иногородними клиентами или даже отдельными клиентами. Естественно, результирующий набор агрегатных данных во втором и третьем случаях будет более детальным, чем в первом. Заметим, что возможность получения агрегатных данных с различной степенью детализации соответствует одному из требований, предъявляемых к хранилищам данных, — требованию доступности различных срезов данных для сравнения и анализа. Поскольку в рассмотренном примере в общем случае в каждой стране может быть несколько городов, а в городе — несколько клиентов, можно говорить об иерархиях значений в измерениях. В этом случае на первом уровне иерархии располагаются страны, на втором — города, а на третьем — клиенты (рисунок 5).
Локаторы куба отличаются иерархической
структурой, и для получения значений мер на каждом уровне агрегирования
вводятся агрегирующие функции.
2.2.
Иерархии и агрегирование.
Иерархичность данных – одно
из важнейших свойств многомерных кубов. Иерархии призваны добавлять новые
уровни в аналитическое пространство пользователя. Самым распространенным
примером иерархии является «день-неделя-месяц-год». Соответственно, для уровней
иерархии работают отношения обобщения и специализации (rollup/drilldown). Как
правило, в научных работах рассматриваются простые примеры иерархий «детальное
значение – ALL», однако, как мы увидим
далее, подобного уровня детализации может быть недостаточно.
Отметим, что несбалансированные и «неровные» иерархии поддерживаются далеко не всеми OLAP-средствами. Различным в разных OLAP-средствах может быть и число уровней иерархии, и максимально допустимое число членов одного уровня, и максимально возможное число самих измерений.
2.3.
Агрегирующие функции, меры и формулы.
Неотъемлемой частью OLAP-модели
является задание функций агрегирования. Поскольку целью OLAP является создание
многоуровневой модели анализа, данные на уровнях, отличных от фактического,
должны быть соответствующим образом агрегированы. Важно отметить, что по
каждому измерению можно задавать собственную (и не одну) функцию агрегации.
В [3] приведена следующая классификация
агрегирующих функций с точки зрения сложности распараллеливания.
1. Дистрибутивные функции
позволяют разбивать входные данные и вычислять отдельные итоги, которые потом
можно объединять.
2. Алгебраические функции
можно представить комбинацией из дистрибутивных функций (например, Average()
можно представить как сумму, разделенную на count).
3. Холистические функции
невозможно вычислять на частичных данных или представлять каким-либо образом.

2.4. Виды запросов к
кубам.
1.
Точечные запросы (Point queries). При
запросах этого вида возвращается агрегирующее значение меры в какой-то ячейке
куба, координаты которой задаются в запросе. Все прочие запросы можно
переписать, используя серии точечных запросов. Поэтому время выполнения
точечных запросов является одной из важнейших характеристик алгоритма хранения
OLAP данных.
ПРИМЕР.
SELECT регион, продукт, время,
SUM(продажи) FROM Продажи
WHERE (регион = R1) AND (продукт =
книги) AND (время = весна)
Результат:
ячейка (R1, книги, весна).
2. Интервальные запросы (Range
queries). При запросах этого вида возвращается
некоторый набор точек куба, удовлетворяющий заданным условиям.
ПРИМЕР.
SELECT регион, продукт, SUM(продажи)
FROM Продажи
WHERE ((регион = R1) OR ((регион = R2))
AND ((продукт = книги) OR (продукт = еда))
GROUP BY регион, продукт
Результат:
продажи книг и еды в R1 и R2.
3. Обратные запросы (Iceberg
queries). В отличие от точечных и интервальных
запросов, для ответа на запрос данного типа используются значения меры
(агрегирующие значения). Обратный запрос возвращает все ячейки куба, удовлетворяющие
ограничениям, наложенным на значение меры пользователем.
ПРИМЕР.
SELECT регион, продукт, время,
AVG(продажи)
FROM Продажи CUBE BY регион, продут,
время // создается куб
HAVING AVG(продажи) >= 6 // в
условии HAVING заключается ограничение на значение меры. Существует множество
алгоритмов, ориентированных на обработку исключительно обратных запросов.
4. Intelligent Roll-Up запросы.
Алгоритм создания куба для обработки
данного типа запросов. Запрос можно сформулировать следующим образом: «Каковы наиболее общие условия, при которых
значение меры является заданным?».
В отличие от обратных запросов, в
данном типе запросов полностью используются все характеристики кубов
(иерархичность, многомерность). Легко заметить, что SQL-запросы в таком случае
будут иметь сложную структуру, т.к. необходимы именно наиболее общие условия,
т.е. максимальные с точки зрения иерархий измерений точки многомерного
пространства.
Отметим, что алгоритм Quotient Cube и представление куба с
помощью верхних граней обеспечивают быстрый ответ на подобные запросы, т.к. по
определению верхняя грань разбиения и есть наиболее общее условие равенства
меры определенному значению.

- ХРАНЕНИЕ И ЭФФЕКТИВНЫЙ РАСЧЕТ OLAP-КУБОВ.
Основными задачами, возникающими при
хранении OLAP-данных, считаются хранение разреженных данных и эффективный
расчет экспоненциального количества агрегатов, возникающих при добавлении
фактических данных (так называемый «взрыв данных»).
3.1.
Представление неопределенных данных.
Одним из важнейших свойств OLAP-систем
считается эффективное хранение «неопределенных данных», поскольку создание
многомерных структур порождает появление большого числа точек многомерного
пространства, не содержащих значений мер. Например, при формировании куба
появляются точки, для которых не было фактических данных, вроде (R2, весна,
еда).
В рассматриваемых алгоритмах, как и во
многих других, предлагается следующее решение: не хранить неопределенные
значения и, в случае отсутствия данных в кубе, возвращать нулевые значения.
Однако данная проблема схожа с
проблемой NULL-значений в базах данных.
Возможны следующие случаи отсутствия
данных в кубе:
- данных
быть не может, значение не может существовать;
- нулевые данные;
- данные еще не получены, необходимо использовать некую
формулу для получения значения.
Оставим без рассмотрения случай 3,
несмотря на то, что он очень важен для анализа (например, если пользоваться
прогнозированием с поквартальным уточнением факта).
В первых двух случаях возникает
следующая ситуация. Отсутствие данных в кубе означает следующее: либо они
нулевые, либо их быть не может. Разница между данными понятиями становится
очевидной при необходимости применения функции Average(), т.к. от данного
понятия зависит величина Count().
ПРИМЕР.
Например,
если магазин рапортовал о нулевых продажах товара, он все равно должен попасть
в число магазинов, товар продававших.
Данный момент очень важен для
построения корректной системы анализа.
3.2.
Взрыв данных.
При добавлении исходных данных в куб объем
данных и время вычисления куба растут экспоненциально, так как необходимо
рассчитывать агрегаты по каждому из измерений.
ПРИМЕР.
Например,
десятимерный куб без иерархии внутри измерений с размерностью 100 для
каждого измерения приводит к структуре со 10110 ячейками. Даже если мы положим разреженность 1
к 106 (т.е.
пусть только одна из миллиона ячеек содержит данные), куб все равно будет иметь
(1,1)14 непустых ячеек.
Если пустые значения достаточно легко
сжимаются, то «взрывом данных» называют рост количества агрегатов по всем
измерениям, которые необходимо вычислить. Таким образом, сокращение размера
куба – насущная задача создателей OLAP-приложений. Для устранения подобных
ситуаций в каждом из алгоритмов используются специальные техники (например,
condensed-ячейки в алгоритме Condensed Cube).
3.3.
Материализация представлений.
Главным свойством OLAP-систем считается
возможность эффективно отвечать на запросы. Одной из мер повышения
эффективности выполнения запросов является материализация кубов, а не
вычисление их «на лету» (вычисление агрегаций непосредственно во время
обработки запроса).
Считается стандартным представление
куба в виде так называемой структуры (cube lattice) – графа, в котором узлы
определяют представления (view) для ответа на запрос. Для каждого узла пометка
обозначает измерения, по которым в представлении имеются фактические данные, по
значениям ALL производится агрегация. На рисунке 7 показана структура куба.
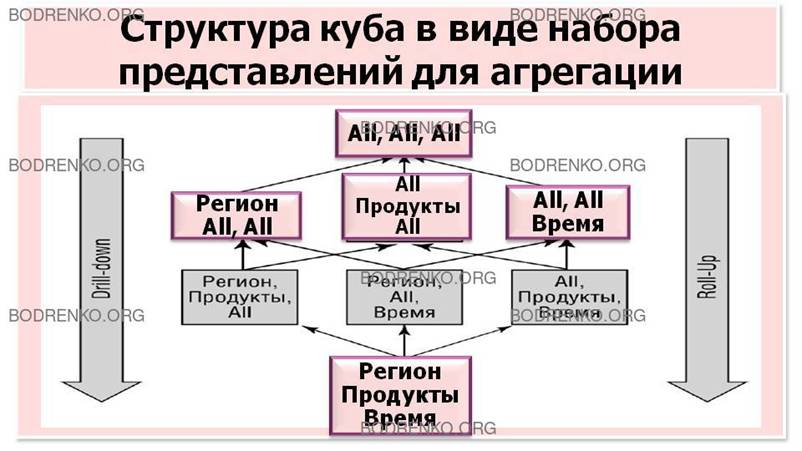
Рисунок
7. Структура куба в виде набора
представлений для агрегации.
Таким образом, в получившейся структуре
куба материализуется набор представлений, содержащий агрегированные данные.
Подобные представления также называются подкубами (cuboids).
Ячейки базового подкуба называются
также базовыми ячейками, ячейки
других подкубов называются агрегированными
ячейками.
Выбор подкубов для материализации
определяет будущую производительность системы. Мы можем получить набор
представлений, при использовании которого для выполнения запросов будет не
производиться более 1-2 агрегаций (по одному измерению), что означает очень
быстрый ответ на запрос. И наоборот, возможна ситуация, в которой для ответа на
запрос необходимо будет создавать все агрегации от фактических данных (базового
куба). Однако количество подкубов экспоненциально зависит от количества
измерения (как 2n , где n
— количество измерений), поэтому для полной материализации может требоваться
огромный объем памяти и места на жестком диске.
ПОЛНАЯ МАТЕРИАЛИЗАЦИЯ.
Изучение алгоритмов полной
материализации помогает в расчетах индивидуальных подкубов, которые в
дальнейшем можно хранить на второстепенных носителях, или же создавать полные
кубы на основе подмножества измерений и осуществлять детализацию (drill-down) в
исходные данные в случае необходимости. Подобные алгоритмы должны быть
масштабируемыми, принимать во внимание ограниченное количество оперативной
памяти, время вычисления и общий размер рассчитанных данных.
ЧАСТИЧНАЯ МАТЕРИАЛИЗАЦИЯ.
Частичная материализация предлагает
выбор между временем создания кубов и размером хранимых данных, с одной
стороны, и временем отклика, с другой. Вместо вычисления полного куба мы можем
вычислить лишь некоторые из его подкубов или даже частей подкубов.
Множество работ посвящено выбору набора
представлений (подкубов) для материализации.
Модель оценки стоимости материализации
представлений и создания агрегаций. На базе подобных оценок создан алгоритм
материализации представлений, оптимизирующий запросы по стоимости. Однако
применимость алгоритма и многих последующих алгоритмов сильно ограничена
(например, типами запросов,
распределением данных, структурой куба и пр.). Ограничения накладываются самими
авторами, за счет чего часто создаются эффективные алгоритмы. Доказано, что
общая проблема выбора представлений для материализации NP-полна.
3.4.
Iceberg-кубы.
Многие ячейки кубов могут не
представлять интереса для аналитиков, так как данные в них пренебрежимо малы.
Подобная ситуация часто возникает, так как данные разреженно распределены в
многомерном пространстве куба.
ПРИМЕР.
К
примеру, клиент покупает каждый раз лишь несколько товаров в одном магазине.
Подобное событие будет отражено в виде набора ячеек с малыми показателями мер
(объем покупки, количество предметов). В таких случаях полезно предвычислять лишь
ячейки со значением меры, большим определенной границы. К примеру, нас будут
интересовать лишь покупки на сумму свыше 500 рублей. Такой подход позволяет
точнее сфокусировать анализ, не говоря о сокращении времени вычисления и
времени отклика.
Подобные частично вычисленные кубы
называются кубами-айсбергами (англ. iceberg cubes), так как представляют собой
вершину айсберга, большая часть которого скрыта под водой. Такие кубы создаются
запросами типа Iceberg (см. Обратные запросы).
Простым представляется следующий подход
к вычислению кубов-айсбергов: сначала вычислить весь куб, затем применить
условие и отрезать неудовлетворяющие ячейки. Однако это слишком расточительный
подход, необходимо вычислять куб-айсберг, не вычисляя полный куб.
Однако даже использование ограничений
на значение меры может приводить к ситуациям, требующим бессмысленных повторных
вычислений. К примеру, в 100-мерном кубе существуют всего 2 ячейки,
отличающиеся по значениям одного из измерений. Если меры в этих ячейках больше
заданной границы, то будут порождены множество дублирующих эти суммы ячеек
(суммы по всем 99 измерениям). И это при
том, что в кубе вообще 3 различные ячейки. Для обработки подобных случаев
используется концепция покрытий ячеек.
3.5. Общие стратегии вычисления кубов.
Вне зависимости от метода хранения
(ROLAP, MOLAP и др.), существует набор приемов, позволяющих уменьшить время
создания и обработки запросов к OLAP-кубам.
1. Сортировка, хеширование,
группировка.
Во время вычисления куба агрегируются
кортежи (или ячейки), имеющие одинаковые значения по всем измерениям (так
называемые дубликаты), поэтому важно использовать сортировки и группировать
данные, чтобы упростить вычисление подобных агрегатов. К примеру, если
необходимо посчитать общие продажи по регионам, продуктам, времени года, то
более эффективно сортировать кортежи по регионам, затем по по дням и
группировать по продуктам. Эффективной реализации подобных операций с большими
объемами данных посвящено немало работ в области баз данных. Используемые в
этой области алгоритмы могут быть адаптированы для вычислений кубов.
Подобный подход может быть также
расширен до разделяемых сортировок (т.е. использованию отсортированных
результатов для создания многих подкубов, что позволяет распределить затраты на
сортировку) или до разделяемого партиционирования (т.е. разделения затрат на
партиционирование при использовании хэширования).
2. Одновременные агрегирование и
кэширование промежуточных результатов.
Эффективнее создавать подкубы высоких
уровней из подкубов низких уровней, нежели из базовой таблицы. Более того,
одновременное вычисление агрегатов может позволить сократить дорогостоящие
операции обращения к жестким дискам.
ПРИМЕР.
К
примеру, для расчета продаж по регионам мы используем промежуточные результаты,
полученные при расчете подкуба более низкого уровня продаж по регионам, по
дням.
Расширение подобного подхода может
привести к теории амортизированных чтений (т.е. вычислению максимального
количества подкубов за одно обращение к диску).
3. Агрегирование от наименьшего
подкуба-потомка при наличие многих подкубов-потомков.
При вычислении подкуба высокого порядка
часто более эффективно использовать наименьший из уже рассчитанных
подкубов-потокомков.
ПРИМЕР.
К
примеру, для расчета куба продаж по регионам при условии наличия 2-х
рассчитанных подкубов (по регионам и годам, и по регионам и продуктам),
очевидно, эффективнее использовать куб по регионам и годам, так как он содержит
меньше ячеек.
4. Использование леммы Apriori при
создании кубов типа «айсберг».
Это правило, используемое при создании
кубов типа «айсберг», гласит:
«Если указанная ячейка не удовлетворяет условию,
накладываемому на минимальное значение меры, то ни один из ее потомков не
удовлетворяет условию».
Этот факт был строго доказан и широко применяется в алгоритмах Data Mining.
При вычислении кубов типа «айсберг»
существенную роль играет выбор условия на меру, которому должны удовлетворять
ячейки, чтобы быть включенными в куб. Типичным айсберг-условием является минимальное
значение, ячейки с мерой ниже которого исключаются при расчете (например, сумма
продаж и количество купленных продуктов). В подобной ситуации условие Apriori
может быть использовано для сокращения объема обрабатываемых данных.

ПРИМЕР.
Например,
если количество продаж в ячейке меньше минимально необходимого, то ни в одном
из детей этой ячейки количество продаж указанный порог не превысит.
Однако нужно отметить, что данное
условие верно только для дистрибутивных
агрегирующих функций.
Таким образом, сокращение размера куба
— насущная задача создателей OLAP-приложений. Еще одним важным ограничением
является требование сохранения семантики отношений обобщения/специализации
(roll-up/drill-down). Отбрасывая это требование, многие алгоритмы достигают
хороших результатов, но восстановление этих отношений в дальнейшем либо
невозможно, либо трудно вычислимо, что существенно ограничивает возможность их
применения.
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ.
[1] Барсегян А. А., Куприянов М. С. , Степаненко В. В., Холод И. И. Методы и модели анализа данных: OLAP и Data Mining. – СПб.: БХВ-Петербург, 2004. - 336 с.
[2] Елманова Н., Федоров А. Введение в OLAP-технологии Microsoft. - М.: Диалог-МИФИ, 2002. - 272 с.

[3] Кудрявцев Ю.А. OLAP технологии: обзор решаемых задач и исследований // Бизнес-информатика. – 2008. №1. – С. 66-70.
[4] Фоменко Е.Ю. Хранилища данных. Анализ данных: Курс
лекций. - М.: Ф-т ВМиК МГУ им. М.В. Ломоносова, 2007.
[5] Хоббс Л., Хилсон С., Лоуэнд Ш. Oracle9iR2: разработка и эксплуатация хранилищ баз данных. Учебно-справочное изданиеы. Пер. С англ. - М.: КУДИЦ-ОБРАЗ, 2004. – 592 с.
