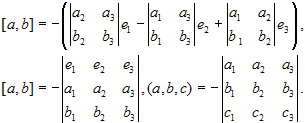Для любых векторов a, b, c(a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) =
- (a, c, b) = - (c, b, a). 4.2.3
Следствие 2. Смешанное произведение линейно по каждому из сомножителей. Это утверждение вытекает из (4.2.2) и линейности скалярного произведения. Доказано.
Теорема 4.10. Векторное произведение линейно по каждому из сомножителей.
Доказательство. В силу теоремы 4.6 достаточно показать, что для любых векторов a, b, c и любого числа α ∈ R имеют
место равенства [a +b, c] = [a, c] + [b, c] и [αa, b] = α[a, b]. Пусть d = [a +b, c] - [a, c] - [b, c]. Тогда (d, d) = (a + b, c, d) - (a, c, d) - (b, c, d). Из линейности смешанного произведения следует, что
(d, d) = (a, c, d) + (b, c, d)- (a, c, d) - (b, c, d) = 0. Это доказывает первое из требуемых равенств. Второе равенство доказывается аналогично. Теорема доказана.
Векторное и смешанное произведения в прямоугольных координатах. Пусть e1, e2, e3
− ортонормированный базис пространства и пусть e1, e2, e3 − правая тройка.
1. Найдем координаты
векторного произведения [a, b], если вектры a = {a1, a2, a3} и b = {b1, b2, b3} заданы своими координатами в базисе
e1, e2, e3. Согласно теоремам 4.5 и 4.10 имеем [a, b] = [a1e1 +a2e2 + a3e2,
b1e1 + b2e2 + b3e3] = a1b1[e1, e2] + a1b3[
e1, e3] + a2b1[e2, e1] + a2b3[e2, e3] + a3b1[
e3, e1] + a3b2[e3, e2]. Отсюда в силу теоремы 4.6 следует, что
Пусть [a, b] = xe1 + ye2 + ze3. Тогда, применяя (4.1.4), теоремы 4.6 - 4.8 и замечание 1 (параграфа 4.2), получаем, что Аналогично Итак, 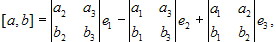
4.2.4
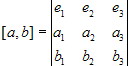
4.2.5
2. Из (4.2.4) и (4.1.5) непосредственно находим и смешанное произведение векторов
a = {a1, a2, a3}, b = {b1, b2, b3}, с = {с1, с2, с3}, заданных своими координатами в ортонормированном
базисе: 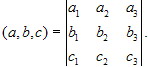
4.2.6
Замечание 1. Если исходный базис e1, e2, e3
отрицательно ориентирован, то (e1, e2, e3) = -1 ( теорема 4.8) и, следовательно, в соотношениях (4.2.4) - (4.2.6) следует поменять знаки на противоположные:
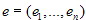 и
и 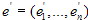 линейного пространства V называются одинаково ориентированными, если матрица перехода Сe→e' имеет положительный определитель,
и противоположно ориентированными − в противном случае.
линейного пространства V называются одинаково ориентированными, если матрица перехода Сe→e' имеет положительный определитель,
и противоположно ориентированными − в противном случае. 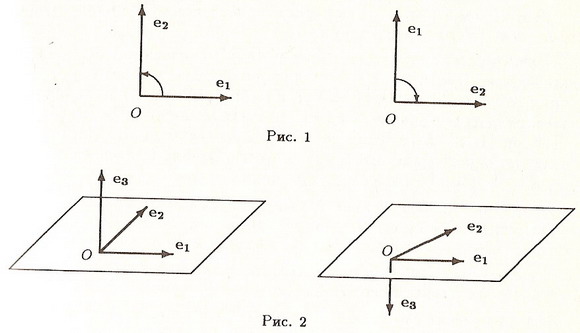
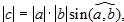
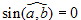 ; это раносильно тому, что |[a, b]| = 0, т.е. [a, b] = 0. Теорема доказана.
; это раносильно тому, что |[a, b]| = 0, т.е. [a, b] = 0. Теорема доказана.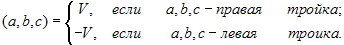
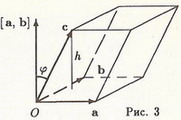 Знак (a, b, c) определяется только знаком cos φ, но cos φ > 0 тогда и только тогда, когда
векторы [a, b] и с направлены в одну сторону от плоскости π(a, b), т.е. тогда и только тогда, когда тройка a, b, c − правая. В силу (4.2.1) отсюда следует утверждение теоремы.
Теорема доказана.
Знак (a, b, c) определяется только знаком cos φ, но cos φ > 0 тогда и только тогда, когда
векторы [a, b] и с направлены в одну сторону от плоскости π(a, b), т.е. тогда и только тогда, когда тройка a, b, c − правая. В силу (4.2.1) отсюда следует утверждение теоремы.
Теорема доказана.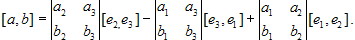
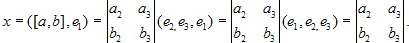
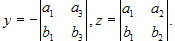
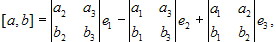 4.2.4
4.2.4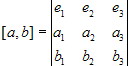 4.2.5
4.2.5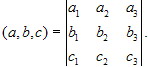 4.2.6
4.2.6