Линейная алгебра. Закон инерции квадратичных форм. Классификация квадратичных форм. Ранг квадратичной формы. Критерий Сильвестра. Метод Якоби. Необходимое и достаточное условие знакоопределенности квадратичной формы. Положительно определенная, отрицательно определенная, знакопеременная квадратичные формы.

Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org    
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость

Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

§ 4. Закон инерции квадратичных форм. Классификация квадратичных форм

1. Закон инерции квадратичных форм. Мы уже отмечали (см. замечание 2 п. 1 предыдущего параграфа), что ранг квадратичной формы равен числу отличных от нуля канонических коэффициентов. Таким образом, число отличных от нуля канонических коэффициентов не зависит от выбора невырожденного преобразования, с помощью которого форма А(х, х) приводится к каноническому виду. На самом деле при любом способе приведения формы А(х, х) к каноническому виду не меняется число положительных и отрицательных канонических коэффициентов. Это свойство называется законом инерции квадратичных форм.
Прежде чем перейти к обоснованию закона инерции, сделаем некоторые замечания.
Пусть форма А(х, х) в базисе е = (е₁, е₂,..., е_n) определяется матрицей А(е) = (а_ij):

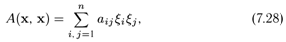
где ξ₁, ξ₂, ..., ξ_n - координаты вектора х в базисе е. Допустим, что эта форма с помощью невырожденного преобразования координат приведена к каноническому виду

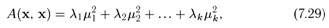
причем λ₁, λ₂,..., λ_k — отличные от нуля канонические коэффициенты, занумерованные так, что первые q из этих коэффициентов положительные, а следующие коэффициенты — отрицательные:

λ₁ > 0, λ₂ > 0, ..., λ_q > 0, λ_q+1 < 0, ..., λ_k<0.

Рассмотрим следующее невырожденное преобразование координат μ_i (легко видеть, что определитель этого преобразования отличен от нуля) :

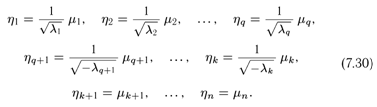
В результате этого преобразования форма А(х, х) примет вид

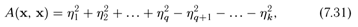
называемый нормальным видом квадратичной формы. 
Итак, с помощью некоторого невырожденного преобразования координат ξ₁, ξ₂, ..., ξ_n вектора х в базисе е = (е₁, е₂,..., е_n)

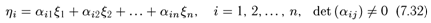
(это преобразование представляет собой произведение преобразований ξ в μ и μ в η пo формулам (7.30)) квадратичная форма может быть приведена к нормальному виду (7.31).
Докажем следующее утверждение.
Теорема 7.5 (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами в нормальном виде квадратичной формы не зависит от способа приведения формы к этому виду.
Доказательство. Пусть форма А(х, х) с помощью невырожденного преобразования координат (7.32) приведена к нормальному виду (7.31) и с помощью другого невырожденного преобразования координат приведена к нормальному виду

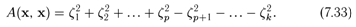
Очевидно, для доказательства теоремы достаточно убедиться в справедливости равенства р = q.
Пусть р > q. Убедимся, что в этом случае имеется ненулевой вектор х такой, что по отношению к базисам, в которых форма А(х, х) имеет вид (7.31) и (7.33), координаты η₁, η₂, ..., η_q и ζ_р+1, ..., ζ_n этого вектора равны нулю:

η₁ = 0,   η₂ = 0,   ...,   η_q = 0,    ζ_р+1 = 0,   ...,   ζ_n  = 0           (7.34)

Так как координаты η_i получены путем невырожденного преобразования (7.32) координат ξ₁, ..., ξ_n, а координаты ζ_i — с помощью аналогичного невырожденного преобразования этих же координат ξ₁, ..., ξ_n, то соотношения (7.34) можно рассматривать как систему линейных однородных уравнений относительно координат ξ₁, ..., ξ_n искомого вектора х в базисе е = (е₁, е₂,..., е_n) (например, в развернутом виде соотношение η₁ = 0 имеет, согласно (7.32), вид а₁₁ξ₁ + а₁₂ξ₂ + а_1nξ_n = 0)- Так как р > q, то число однородных уравнений (7.34) меньше n, и поэтому система (7.34) имеет ненулевое решение относительно координат ξ₁, ..., ξ_n искомого вектора х. Следовательно, если р > q, то существует ненулевой вектор х, для которого выполняются соотношения (7.34).
Подсчитаем значение формы А(х, х) для этого вектора х. Обращаясь к соотношениям (7.31) и (7.33), получим

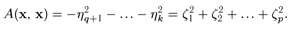
Последнее равенство может иметь место лишь в случае η_q+1 = ... = η_k = 0 и ζ₁ = ζ₂ = ... = ζ_р = 0.
Таким образом, в некотором базисе все координаты ζ₁, ζ₂, ..., ζ_n ненулевого вектора х равны нулю (см. последние равенства и соотношения (7.34)), т.е. вектор х равен нулю. Следовательно, предположение р > q ведет к противоречию. По аналогичным соображениям ведет к противоречию и предположение р < q.
Итак, р = q. Теорема доказана.
2. Классификация квадратичных форм. В п. 1 §2 этой главы (см. определение 2) были введены понятия положительно определенной, отрицательно определенной, знакопеременной и квазизнакоопределенной квадратичных форм.
В этом пункте с помощью понятий индекса инерции, положительного и отрицательного индексов инерции квадрата формы мы укажем, каким образом можно выяснить принадлежность квадратичной формы к тому или иному из перечисленных выше типов. При этом индексом инерции квадратичной формы будем называть число отличных от нуля канонических коэффициентов этой формы (т.е. ее ранг), положительным индексом инерции — число положительных канонических коэффициентов, отрицательным индексом инерции — число отрицательных канонических коэффициентов. Ясно, что сумма положительного и отрицательного индексов инерции равна индексу инерции.
Итак, пусть индекс инерции, положительный и отрицательный индексы инерции квадратичной формы А(х, х) соответственно равны k, p и q (k = p + q).B предыдущем пункте было доказано, что в любом каноническом базисе f = (f₁, f₂, ..., f_n) эта форма может быть приведена к следующему нормальному виду:

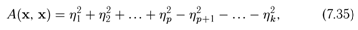
где η₁, η₂, ..., η_n — координаты вектора х в базисе f.
1°. Необходимое и достаточное условие знакоопределенности квадратичной формы. Справедливо следующее утверждение.
Для того чтобы квадратичная форма А(х, х), заданная в n-мерном линейном пространстве L, была знакоопределенной, необходимо и достаточно, чтобы либо положительный индекс инерции р, либо отрицательный индекс инерции q был равен размерности n пространства L.
При этом, если р = n, то форма положительно определенная, если же q = n, то форма отрицательно определенная.
Доказательство. Так как случаи положительно определенной формы и отрицательно определенной формы рассматриваются аналогично, то доказательство утверждения проведем для положительно определенных форм.
1) Необходимость. Пусть форма А(х, х) положительно определена. Тогда выражение (7.35) примет вид

А(х,х) = η₁² + η₂² + ... + η_р².

Если при этом р < n, то из последнего выражения следует, что для ненулевого вектора х с координатами

η₁ = 0,   η₂ = 0,   ...,   η_р = 0,    η_р+1 ≠ 0,   ...,   η_n  ≠ 0

форма А(х, х) обращается в нуль, а это противоречит определению положительно определенной квадратичной формы. Следовательно, р = n.
2) Достаточность. Пусть р = n. Тогда соотношение (7.35) имеет вид А(х,х) = η₁² + η₂² + ... + η_р². Ясно, что А(х, х) ≥ 0, причем, если А = 0, то η₁ = η₂ = ... = η_n = 0, т. е. вектор х нулевой. Следовательно, А(х, х) — положительно определенная форма.
Замечание. Для выяснения вопроса о знакоопределенности квадратичной формы с помощью указанного признака мы должны привести эту форму к каноническому виду.
В следующем пункте мы докажем критерий Сильвестра знакоопределенности квадратичной формы, с помощью которого можно выяснить вопрос о знакоопределенности формы, заданной в любом базисе без приведения к каноническому виду.
2°. Необходимое и достаточное условие знакопеременности квадратичной формы. Докажем следующее утверждение.
Для того чтобы квадратичная форма была знакопеременной, необходимо и достаточно, чтобы как положительный, так и отрицательный индексы инерции этой формы были отличны от нуля.
Доказательство. 1) Необходимость. Так как знакопеременная форма принимает как положительные, так и отрицательные значения, то ее представление G.35) в нормальном виде должно содержать как положительные, так и отрицательные слагаемые (в противном случае эта форма принимала бы либо неотрицательные, либо неположительные значения). Следовательно, как положительный, так и отрицательный индексы инерции отличны от нуля.
2) Достаточность. Пусть р ≠ 0 и q ≠ 0. Тогда для вектора x₁, с координатами η₁ ≠ 0, ..., η_р ≠ 0,    η_р+1 = 0,   ...,   η_n  = 0 имеем А(х₁ x₁) > 0, а для вектора х₂ с координатами η₁ = 0, ..., η_р = 0, η_р+1 ≠ 0, ..., η_n  ≠ 0 имеем А(х₂, х₂) < 0. Следовательно, форма А(х, х) является знакопеременной.
3°. Необходимое и достаточное условие квазизнакоопределенности квадратичной формы. Справедливо следующее утверждение.
Для того чтобы форма А(х, х) была квазизнакоопределенной, необходимо и достаточно, чтобы выполнялись соотношения: либо р < n, q = 0, либо р = 0, q < n.
Доказательство. Мы рассмотрим случай положительно квазизнакоопределенной формы. Случай отрицательно квазизнакоопределенной формы рассматривается аналогично.
1) Необходимость. Пусть форма А(х, х) положительно квазизнакоопределенная. Тогда, очевидно, q = 0 и р < n (если бы р = n, то форма была бы положительно определенной),
2) Достаточность. Если р < n, q = 0, то А(х, х) ≥ 0 и для ненулевого вектора х с координатами η₁ = 0, η₂ = 0, ..., η_р = 0, η_р+1 ≠ 0, ..., η_n  ≠ 0 имеем А(х, х) = 0, т.е. А(х, х) — положительно квазизнакоопределенная форма.
3. Критерий Сильвестра (Джемс Джозеф Сильвестр (1814-1897) — английский математик) знакоопределенности квадратичной формы. Пусть форма А(х, х) в базисе е = (е₁, е₂,..., е_n) определяется матрицей А(е) = (а_ij):

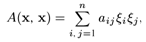
и пусть Δ₁ = а₁₁, - угловые миноры и определитель матрицы (а_ij). Справедливо следующее утверждение.
Теорема 7.6 (критерий Сильвестра). Для того чтобы квадратичная форма А(х, х) была положительно определенной, необходимо и достаточно, чтобы были выполнены неравенства Δ₁ > 0, Δ₂ > 0, ..., Δ_n > 0.
Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем Δ₁ < 0.
Доказательство. 1) Необходимость. Докажем сначала, что из условия знакоопределенности квадратичной формы А(х, х) следует Δ_i ≠ 0, i = 1, 2,..., n.
Убедимся, что предположение Δ_k = 0 ведет к противоречию — при этом предположении существует ненулевой вектор х, для которого А(х, х) = 0, что противоречит знакоопределенности формы.
Итак, пусть Δ_k = 0. Рассмотрим следующую квадратную однородную систему линейных уравнений:

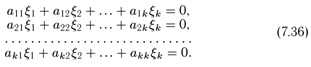
Так как Δ_k — определитель этой системы и Δ_k = 0, то система имеет ненулевое решение ξ₁, ξ₂, ..., ξ_k (не все ξ_i равны 0). Умножим первое из уравнений (7.36) на ξ₁, второе на ξ₂, ..., последнее на ξ_k и сложим полученные соотношения. В результате получим равенство 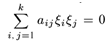, левая часть которого представляет собой значение квадратичной формы А(х, х) для ненулевого вектора х с координатами (ξ₁, ξ₂, ..., ξ_k, 0, ..., 0). Это значение равно нулю, что противоречит знакоопределенности формы.
Итак, мы убедились, что Δ_i ≠ 0, i = 1, 2,..., n. Поэтому мы можем применить метод Якоби приведения формы А(х, х) к сумме квадратов (см. теорему 7.4) и воспользоваться формулами (7.27) для канонических коэффициентов λ_i. Если А(х, х) — положительно определенная форма, то все канонические коэффициенты положительны. Но тогда из соотношений (7.27) следует, что Δ₁ > 0, Δ₂ > 0, ..., Δ_n > 0. Если же А(х, х) — отрицательно определенная форма, то все канонические коэффициенты отрицательны. Но тогда из формул (7.27) следует, что знаки угловых миноров чередуются, причем Δ₁ < 0.
2) Достаточность. Пусть выполнены условия, наложенные на угловые миноры Δ_i в формулировке теоремы. Так как Δ_i ≠ 0, i = 1, 2,..., n, то форму А можно привести к сумме квадратов методом Якоби (см. теорему 7.4), причем канонические коэффициенты λ_i могут быть найдены по формулам (7.27). Если Δ₁ > 0, Δ₂ > 0, ..., Δ_n > 0, то из соотношений (7.27) следует, что все λ_i > 0, т. е. форма А(х, х) положительно определенная. Если же знаки Δ_i чередуются и Δ₁ < 0, то из соотношений (7.27) следует, что форма А(х, х) отрицательно определенная. Теорема доказана.

Bodrenko.org