Теория игр. Бесконечные игры. Бесконечные антагонистические игры. Игры с выбором момента времени. Игры с известными пространствами стратегий. Бесконечной антагонистической игры с непрерывной выпуклой функцией выигрышей. Верхняя цена игры. Нижняя цена игры. Дифференциальная игра поиска. Седловая точка
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Теория игр
Лекция
6
Тема
лекции 6: «Бесконечные игры»

Разделы лекции:
1. Бесконечные антагонистические игры.
2. Игры с выбором момента времени.
3. Игры с известными пространствами
стратегий.

РАЗДЕЛ 1. БЕСКОНЕЧНЫЕ АНТАГОНИСТИЧЕСКИЕ ИГРЫ.
ЧТО ТАКОЕ БЕСКОНЕЧНАЯ АНТАГОНИСТИЧЕСКАЯ
ИГРА?
Естественным обобщением матричных игр
являются бесконечные антагонистические игры, в которых хотя бы один из игроков
имеет бесконечное количество возможных стратегий. В этом разделе мы рассмотрим
игры двух игроков, делающих по одному ходу, и после этого происходит
распределение выигрышей. При формализации реальной ситуации с бесконечным
числом выборов можно каждую стратегию сопоставить определенному числу из
единичного отрезка [0,1], так как всегда можно простым преобразованием любой
отрезок [a,
b]
перевести в единичный отрезок [0, 1] и наоборот.
Для дальнейшего изложения теории игр
этого класса введем определения и обозначения:
[0, 1] — единичный отрезок, из которого
игрок может делать выбор;
х — число (стратегия), выбираемое
первым игроком A;
у — число (стратегия), выбираемое
вторым игроком B;
Обозначим через Г (X, Y, H) игру двух
игроков с нулевой суммой, в которой первый игрок A выбирает число х из множества X, второй —
число у из множества Y,
после чего первый игрок получает выигрыш H(х, у) за счет второго игрока.
Дадим следующее определение.
ОПРЕДЕЛЕНИЕ. Игра Г(X, Y, H) двух игроков с нулевой суммой,
заключающаяся в выборе первым игроком числа х из множества X, вторым игроком
числа y из множества Y, и с дальнейшим получением выигрыша H(х,y) первым игроком за счет второго,
называется бесконечной антагонистической
игрой, если хотя бы одно из множеств X или Y содержит бесконечное количество элементов (чисел).

Для решения такой игры можно поступить
по аналогии с матричными играми, однако, в этом случае задача очень
усложняется. Большое значение имеет вид функции выигрышей H(х, у). В
зависимости от вида функций классифицируются игры и разрабатываются методы их
решений. Оказывается, не для всякой функции H(х, у) существует решение (в отличие от
матричных игр). Будем считать, что выбор определенного числа игроком означает
применение его чистой стратегии, соответствующей этому числу.
ЧТО ТАКОЕ НИЖНЯЯ И ВЕРХНЯЯ ЦЕНА
БЕСКОНЕЧНОЙ АНТАГОНИСТИЧЕСКОЙ ИГРЫ?
По аналогии с матричными играми назовем
чистой нижней ценой игры величину
V1 = max inf H(х, у)
х
у
или
V1 = max min H(х, у),
x∈X у∈Y
а чистой верхней ценой игры назовем величину
V2 = min sup H(х, у)
y
x
или
V2 = min max H(x,
y).
y∈Y x∈X

Для матричных игр величины V1 и V2 всегда
существуют, а в бесконечных играх они могут не существовать. Естественно
считать, что, если для какой-либо бесконечной игры величины V1 и V2 существуют и равны между собой (V1 = V2 =V),
то такая игра имеет решение в чистых стратегиях, т. е. оптимальной стратегией
первого игрока есть выбор числа х0, принадлежащего множеству X, и второго игрока — числа у0, принадлежащего
множеству Y, при которых H(х0,
у0) = V, в этом случае V называется ценой игры, а (х0, у0) — седловой точкой в
чистых стратегиях.
Рассмотрим следующий пример.
ПРИМЕР 1.
Первый игрок A выбирает число х из множества X,
которое представляет собой замкнутый промежуток [0, 1], второй игрок B выбирает
число у из множества Y, представляющего замкнутый промежуток [0, 1]. После
этого второй игрок платит первому сумму H(х, у) = 2х∙x — у∙y.

Поскольку второй игрок хочет
минимизировать выигрыш первого игрока, то он определяет
min H(x,y) = min (2х∙x — у∙y) = 2х∙x — 1,
y∈Y y∈Y
т. е. при этом у = 1.
Первый игрок желает максимизировать
свой выигрыш, и поэтому определяет чистую нижнюю цену игры V1:
V1 = max (min H(х, у)) = max (2х∙x
— 1) = 2 – 1 = 1.
x∈X
у∈Y x∈X
который достигается при х = 1. Итак,
нижняя цена игры равна Vl = 1.

Верхняя цена игры
V2 = min (max
H(x, y)) = min (2 — у∙y) = 2 – 1 = 1.
y∈Y
x∈X y∈Y
т. е. в этой игре V1 = V2 =1. Поэтому
цена игры V = 1, а седловая точка в чистых стратегиях (1,1).

Можно показать, что существование
седловой точки в смешанных стратегиях игры Г(X,Y,H)
равносильно существованию верхней V2 и нижней V1 цен игры в смешанных
стратегиях и их равенству V1 = V2 = V. Таким образом, решить игру Г(X, Y, H) означает найти
седловую точку или такие смешанные стратегии, при которых нижняя и верхняя цены
игры совпадают.
Теперь возникает два вопроса:
1. КОГДА СУЩЕСТВУЕТ РЕШЕНИЕ НЕПРЕРЫВНОЙ
ИГРЫ Г(X, Y, H)?
2. КАКИМИ МЕТОДАМИ НАЙТИ РЕШЕНИЯ ИГРЫ
Г(X, Y, H)?
Ответ на первый вопрос не аналогичен
ответу в матричных играх. Оказывается, что не для всякой бесконечной
антагонистической игры Г (X, Y, H) существует решение. Имеет место следующее утверждение – основная теорема теории непрерывных игр на
единичном квадрате.
ТЕОРЕМА 1. Всякая антагонистическая
бесконечная игра двух игроков Г с непрерывной функцией выигрышей H(х,
у) на единичном квадрате [0, 1]´[0,
1] имеет решение (игроки имеют оптимальные смешанные стратегии).

Таким образом, теорема 1 дает ответ на
первый вопрос о существовании решения бесконечной антагонистической игры.
Справедливо следующее утверждение.
ТЕОРЕМА 2. Пусть в бесконечной антагонистической
игре двух игроков Г(X,
Y,
H)
функция выигрышей H(х, у) непрерывная для х∈[0,
1], у∈[0,
1], и H(х, у) = —H(у, х), тогда цена игры равна нулю (V=0), любая оптимальная стратегия одного
игрока будет также оптимальной стратегией другого игрока.

КАКИЕ БЕСКОНЕЧНЫЕ АНТАГОНИСТИЧЕСКИЕ
ИГРЫ НАЗЫВАЮТСЯ ВЫПУКЛЫМИ?
Сформулированные свойства оптимальных
смешанных стратегий и цены игры помогают находить или проверять решения, но они
еще не дают в общем виде ответа на
вопрос о приемлемых методах решения игры. Поэтому рассматриваются частные виды
антагонистических бесконечных игр. Одним из интересных классов
антагонистических бесконечных игр, для которых легко находить решения, являются
игры с выпуклыми непрерывными функциями выигрышей. Такие игры будем называть выпуклыми.
Напомним, что выпуклой функцией f (x)
действительной переменной х на интервале (а,b) называется такая функция, для которой
выполняется неравенство
f(λ1x1 + λ2x2) ≤ λ1f(x1) + λ2f(x2),
где х1 и х2 — любые две точки из
интервала (а, b);
λ1 и λ2 — неотрицательные числа, причем λ1+ λ2 =1.
Если для λ1≠ 0, λ2 ≠0 всегда имеет место строгое
неравенство
f(λ1x1 + λ2x2) < λ1f(x1) +
λ2f(x2),
то функция f(x)
называется строго выпуклой на интервале (а,b).

Геометрически выпуклая функция
изображает дугу, график которой расположен ниже стягивающей ее хорды (рисунок 1).
Точка D, лежащая на кривой и имеющая координаты (λ1x1 + λ2x2, f(λ1x1 + λ2x2)),
находится ниже точки B,
имеющей координаты (λ1x1
+ λ2x2,
λ1f(x1) + λ2f(x2)), так как |QD| < |QB|.
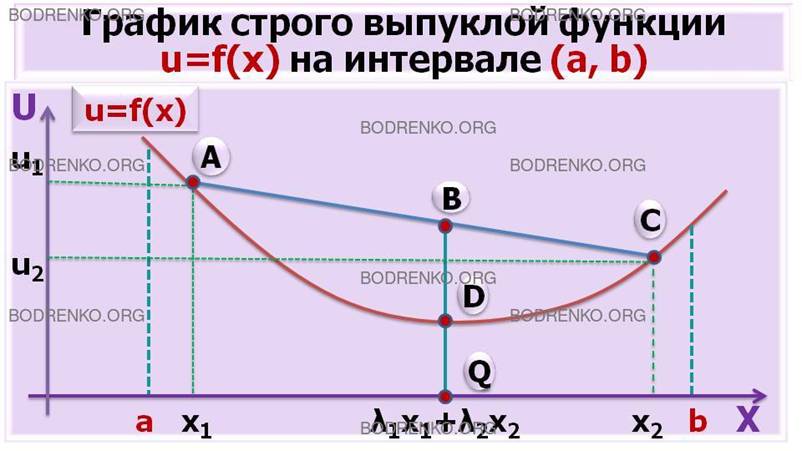
Рисунок 1. График строго выпуклой
функции f(x) на
интервале (a,
b).
Для нахождения решения выпуклой игры
можно воспользоваться следующей теоремой.
ТЕОРЕМА 3. Пусть H(х, у) — непрерывная функция выигрышей
первого игрока игры Г(X,
Y,
H)
на единичном квадрате и строго выпуклая
по у для любого х. Тогда имеется единственная оптимальная чистая стратегия у0∈[0,
1] для второго игрока, цена игры определяется по формуле
V = min max H(х, у), (1)
y x
значение у0 определяется как решение
следующего уравнения
max H(х, у0) = V. (2)
x

ЗАМЕЧАНИЕ.
Если в теореме 3 не предполагать строгую выпуклость функции H(х,у) по у, а
просто выпуклость, то теорема остается в силе с тем отличием, что у второго
игрока оптимальная чистая стратегия не будет единственной.
Итак, если H(х,у) непрерывна и выпукла по у, то
цена игры V
определяется по формуле (1), и второй игрок имеет оптимальную чистую стратегию y0,
определяемую из уравнения (2).
Точно также обстоит дело и для первого
игрока: если функция выигрышей H(х,у)
непрерывна по обоим аргументам и строго вогнута по х при любом у, то в этом
случае первый игрок имеет единственную оптимальную стратегию. Цена игры
определяется по формуле
V = max
min H(х,
у),
x y
а чистая оптимальная стратегия х0
первого игрока определяется из уравнения
min H(х0, у) = V.
y
Рассмотрим пример бесконечной
антагонистической игры с непрерывной выпуклой функцией выигрышей.
ПРИМЕР 2. «БОРЬБА ЗА РЫНКИ».
Две частные фирмы борются за рынки
сбыта в условиях конкуренции. Одна из фирм (первый игрок A) пытается
вытеснить другую фирму (второй игрок B), имеющую два рынка сбыта, с одного из этих рынков. Первый
рынок сбыта приносит доход второму игроку в размере k1 на один рубль проданного
товара, а второй рынок — в размере k2 на один рубль проданного товара. Каждая из фирм выделяет
капитал s для проведения операций.

Стратегии игроков — это количества
средств, выделенных на каждый рынок
сбыта. Обозначим через х количество средств (стратегию), выделяемых первой
фирмой на первый рынок сбыта, тогда (s — х) выделяется первой фирмой на второй рынок
сбыта.

Стратегия второй фирмы аналогична:
чтобы сохранить за собой первый рынок сбыта, она выделяет для него у, а для
второго — сумму (s — у).

Условия борьбы следующие: фирма,
вложившая большую сумму в рынок сбыта, завоевывает его и получает выигрыш,
пропорциональный избытку своих средств.

В этих условиях функция выигрышей
первой фирмы имеет вид:
H(x, y) = k1(x – y), если
x≥y;
H(x, y) = k2(y – x), если x≤ y.
Действительно, если первая фирма
выделяет на первый рынок сбыта больше средств, чем вторая (то есть x > y);
то избыток составит (х — у), а коэффициент дохода равен k1, поэтому доход
первой фирмы составит k1(x — у). Если же первая фирма на первый рынок сбыта
выделяет меньше средств, чем вторая фирма (x < y), значит, первая фирма выделяет больше
средств на второй рынок сбыта, чем вторая, т. е. (s — х) > (s—у). В этом
случае первая фирма получит выигрыш на втором рынке сбыта пропорционально
избытку средств
k2(s – x – (s – y)) =
k2(y – x).
Функция H(х, у) для этой игры непрерывна и выпукла по у при
любом х, поэтому рассматриваемая игра относится к классу игр с выпуклой
функцией выигрышей, и в соответствии с
теоремой 3 игра имеет решение (см: [2]). Цена этой
игры определяется по формуле: V = (k1∙k2∙s)/(k1+k2). Оптимальная
чистая стратегия второго игрока — выделить на первый рынок сбыта у0 средств: y0 = (k1∙s)/(k1+k2), a на второй (s – y0) = s – (k1∙s)/(k1+k2) = (k2∙s)/(k1+k2). Для
определения оптимальной смешанной стратегии первого игрока A найдем
сначала существенные чистые стратегии х из уравнения: H(х, у0) = V. Итак, существенные чистые стратегии первого игрока A – это х0 = s и х1 = 0.

Таким образом, оптимальная стратегия
первого игрока A состоит в концентрации всех средств на
одним из рынков сбыта, а вероятность выбора рынка обратно пропорциональна его
важности. Это согласуется с интуитивным представлением: чем важнее рынок, тем
больше средств вложит в него противник для его сохранения и тем меньше средств
остается на нем после вытеснения противника.
ЗАМЕЧАНИЕ. Бесконечную
игру двух лиц с ненулевой суммой можно определить следующим образом. Обозначим
через Г (X, Y, H1,
H2)
игру двух игроков с ненулевой суммой, в которой первый игрок выбирает число х
из множества X, второй игрок выбирает число у из множества Y, и после этого
первый и второй игроки получают соответственно выигрыши H1(х, у), H2(х,у) (H1(х,у) —
выигрыш 1-го игрока A;
H2(x,y) – выигрыш
2-го игрока B),
и при этом хотя бы одно из множеств X или Y является бесконечным. Если имеет место соотношение: H(x,y) ≡ H1(x,y) = –H2(x,y), то мы приходим
к бесконечной антагонистической игре Г(X,Y,H).
РАЗДЕЛ 2. ИГРЫ С ВЫБОРОМ МОМЕНТА
ВРЕМЕНИ.
Игры с выбором момента времени являются
играми, в которых выбор чистой стратегии представляет собой выбор момента времени для совершения
определенного действия.
1. Предположим, например, что две
большие компании типа «Книга — почтой» намереваются издать свои ежегодные
каталоги. Когда именно следует выпустить каталог — это важный вопрос. Компания,
которая первая выступит со своим каталогом, получает возможность опередить своего конкурента. С другой стороны,
компания, которая ждет дольше, может нажить капитал на недостатках каталога
своего конкурента.
2. Или предположим, что две борющиеся
политические партии пытаются решить,
когда выпустить свои агитационные брошюры. Некоторые люди поддаются первому влиянию, а
потом уже не изменяют своих мнений. На поведение других оказывает влияние
главным образом то, что до них дошло в
последний момент.
3. Следующая задача о выборе момента
времени является обычной задачей в деле книгоиздательства. Две конкурирующие
компании пытаются подписать договор с будущим автором. Момент времени, т. е.
время появления представителя издательства с контрактом и различными
обещаниями, представляет собой чистую стратегию. Слишком ранняя встреча может
оказаться неудачной, так как автор еще не продвинется к тому времени достаточно
далеко в своей работе, чтобы вопрос о ее
опубликовании стал для него актуальным. С другой стороны, предложение может
запоздать: конкурент может к этому времени уже договориться с автором.
Правильный психологический момент является хорошо известным и неоднократно обсуждавшимся понятием в этой игре.
Можно легко придумать множество других
примеров игр с выбором момента времени. Такие игры не обязательно включают одно возможное действие (как в
приведенных примерах), а могут содержать несколько повторных действий.
С математической точки зрения игра с
выбором момента времени описывается как игра, определенная на единичном
квадрате [0, 1]´[0,1],
ядро которой H(x,y) обладает
следующими свойствами:
СВОЙСТВО (1):
H(x, y) = K(x,y), если 0 ≤ x
< y
≤ 1;
H(x, y) = G(x), если x = y;
H(x, y) = L(x,y), если 0 ≤ y
< x
≤ 1.
СВОЙСТВО (2):
Каждая из функций K(x, y) и L(x,y) непрерывна
по совокупности переменных x и y.

СВОЙСТВО (3):
Функция K(x, y) монотонно возрастает по x
для каждого y;
Функция L(x, y) монотонно возрастает по x для каждого y;
Функция K(x, y) монотонно убывает по y для каждого x;
Функция L(x, y) монотонно убывает по y для каждого x.

Переменные x и y следует рассматривать как моменты
времени, в которые действуют противники. Тот факт, что их значения ограничены единичным интервалом, является
условием нормализации и реальных ограничений на модель не накладывает.
Монотонность функций K(x, y) и L(x,y) и разрыв ядра H(x,y) при x = y
можно интерпретировать следующим образом. Если второй
игрок B собирается действовать в фиксированный момент времени y, то первый
игрок A улучшает свои шансы на успех, выжидая, сколько
возможно, при условии, что он действует все же раньше второго игрока B. Если первый
игрок A
дождется того момента, когда совершит
действие второй игрок B,
то он может и проиграть, если игрок B действует успешно. Этим, в сущности, и
объясняется разрыв при x
= y.
Как только второй игрок B
совершил свое действие, шансы на успех первого игрока A возрастают со временем. Это выражается
монотонностью L(x, y) как функции
x.
Аналогичные рассуждения применимы и ко второму игроку B, так как он извлекает пользу всякий
раз, когда уменьшается выигрыш первого игрока
A.
КАКИЕ СУЩЕСТВУЮТ КЛАССЫ ИГР С ВЫБОРОМ МОМЕНТА
ВРЕМЕНИ?
Существует два класса игр с выбором
момента времени.
КЛАСС I.
В первом из них, более простом, функция K(x, y) является
функцией только x,
а функция L(x, y) — функцией
только y.
Мы будем говорить о такой игре как об игре с выбором момента времени в условиях
«полной информации», т. е. в обстановке,
когда действия каждого из игроков, а также последствия этих действий немедленно
становятся известными противнику.
В примере 1 с каталогами компаний «Книга — почтой» игру можно
по очевидным соображениям рассматривать как игру с полной информацией. Примеры
матричных игр с полной информацией показывают, что в этих случаях существуют
оптимальные чистые стратегии.
Рандомизация чистых стратегий возникает
главным образом из-за неопределенностей,
окружающих игрока: если в модели присутствует какая-либо неопределенность, то
оптимальные стратегии почти всегда оказываются
смешанными. В силу этих эвристических замечаний еще одно оправдание названия «игры
с выбором момента времени с полной
информацией» состоит в том, что игры этого класса обычно обладают оптимальными
чистыми стратегиями.
КЛАСС II.
Второй класс состоит из всех игр с
выбором момента времени, не принадлежащих первому классу. То есть ко второму
классу относят игры, в которых функция K, функция L или обе эти функции явно зависят как от
x,
так и от y.
В таких играх действия игрока неизвестны его противнику. Так называемые
бесшумные дуэли являются примерами игр этого типа; другим примером является
описанная выше конкуренция между двумя издательствами в примере 3. Оптимальные
стратегии для игр этого класса обычно представляют собой фактическую
рандомизацию чистых стратегий.
ИГРЫ С ВЫБОРОМ МОМЕНТА ВРЕМЕНИ ПРИ
ОДНОКРАТНОМ ДЕЙСТВИИ КАЖДОГО ИГРОКА.
Важный класс игр на единичном квадрате
состоит из игр, в которых пространствами
чистых стратегий являются сегменты 0 ≤ x ≤ 1 для первого игрока A и 0 ≤ y ≤ 1 для
второго игрока B,
интерпретируемые, как моменты времени, в
которые может быть совершено некоторое действие.
Нормировка 0 ≤ x
≤ 1 и 0 ≤ y
≤ 1 производится здесь только для удобства
и не накладывает существенных ограничений на рассматриваемые модели. В этом
разделе лекции мы ограничимся случаем, в
котором возможно только одно действие для каждого игрока.
ЧТО ТАКОЕ ИГРЫ ТИПА ДУЭЛЕЙ?
Многие игровые ситуации сводятся к
бесконечной антагонистической игре двух игроков, в которой выбор стратегий
отождествляется с выбором момента времени осуществления хода. Они называются
играми типа дуэлей, или играми с выбором момента времени. Конфликтная ситуация,
приводящая к игре типа дуэлей, сводится к следующему: каждый из игроков может
сделать один ход в какой-либо момент из данного промежутка времени, зависящий
от его решения, и получить свой выигрыш. Чем позже он сделает ход, тем больше
вероятность его выигрыша, но, с другой стороны, если он слишком затянет ход, то
другой игрок может сделать свой ход раньше и получить весь выигрыш. Таким
образом, в этой ситуации каждый игрок старается максимально задержать свой ход,
чтобы более уверенно получить выигрыш, но, с другой стороны, он боится слишком
задержать этот ход, так как может потерять выигрыш из-за того, что другой игрок
раньше сделает свой ход. Типичной иллюстрацией таких ситуаций являются дуэли с
огнестрельным оружием, когда каждый участник старается максимально приблизиться
к противнику, чтобы увереннее его поразить, хотя каждый из них опасается, что
слишком большая задержка выстрела даст возможность противнику раньше выстрелить
и поразить его. Если рассматривать бесконечные антагонистические игры на
квадрате, то в играх типа дуэлей функция выигрышей H(х, у) первого игрока разрывна на
диагонали х = у квадрата, где х — момент хода первого игрока, у — момент хода
второго игрока. Рассмотрим некоторые
примеры таких игр. А, именно, вначале рассмотрим
следующую идеализированную модель: каждый из двух противников располагает одним
выстрелом. Иначе говоря, каждый игрок
имеет возможность один раз выстрелить в своего противника, зная при этом, что меткость, т. е.
вероятность успешного выстрела,
возрастает со временем. В игре такого типа выигрыш существенно зависит от
порядка, в котором действуют игроки, и от их индивидуальных способностей
попадания. Очевидно, что каждый игрок хочет задержать свой выстрел насколько
это возможно, чтобы увеличить свою вероятность попадания, но в то же время
стремится не задерживать его настолько, чтобы быть убитым противником. Оптимальная стратегия выражает надлежащее
равновесие между желанием задержки и
опасностью промедления. Многочисленные варианты военных игр с выбором момента времени могут быть сформулированы в терминах
информации, которую игрок имеет относительно поведения противника. Несколько
примеров таких игр мы опишем на лекции. Хотя мы употребляем терминологию
тактических дуэлей, можно интерпретировать
большинство наших моделей также в терминах конкуренции рекламных кампаний и т.
д. Необходимая основа для анализа игр с
выбором момента времени приведена, например,
в монографии С. Карлина [2].
Напомним, что математически игра с выбором момента времени задается функцией
выигрыша H(x, y) определенной на единичном квадрате и
обладающей свойствами (1), (2), (3), сформулированными выше. Наконец, напомним,
что игра с выбором момента времени принадлежит
классу I, если K(x,y) является
функцией, зависящей только от x,
a функция L(x,y) является
функцией, зависящей только от y,
и классу II в противном случае.
ПРИМЕРЫ ИГР С ВЫБОРОМ МОМЕНТА ВРЕМЕНИ.
Хотя общая теория игр с выбором момента
времени охватывает приводимые ниже примеры как частные случаи, их рассмотрение полезно
по двум причинам.
(1) оно дает возможность описать общий
метод определения оптимальных стратегий в простых ясных выражениях, не принимая
в расчет бездну случаев, встречающихся в общей ситуации;
(2) оно помогает иллюстрировать идеи,
лежащие в основе общей теории игр с выбором момента времени.
ПРИМЕР 3. «ШУМНАЯ ДУЭЛЬ».
Каждому из двух дуэлянтов разрешается выстрелить только один раз.
Предположим, что оба они имеют «шумные» пистолеты, так что каждый знает, когда
выстрелил его противник. Ясно, что это игра с выбором момента времени, относящаяся к классу I. Термин «шумный» будет употребляться для того, чтобы обозначить
наличие полной информации, т. е. такое положение дел, при котором каждый игрок
знает, что делает и что сделал другой. Предполагается, что функция меткости p(x) (вероятность
успеха) игрока A
непрерывна, монотонно возрастает по x и p(0) = 0, p(1) = 1. Аналогично точность выстрела
игрока B описывается
непрерывной возрастающей функцией q(y),
q(0)
= 0, q(1)
= 1.

Если первый игрок A поражает второго игрока B, то выигрыш
игрока A полагается равным (+1); если второй игрок
B
поражает игрока A,
то игрок A
получает (— 1); ядром игры H(x,у) будет
ожидаемый выигрыш игрока A, когда
игроки употребляют чистые стратегии x и y.
Структура информации в этой игре (тот
факт, что оружие шумное) принимается
теперь во внимание при составлении функции выигрыша. Если x < у, то вероятность того, что первый
игрок A
поразит игрока B, равна p(x), и выигрыш игрока A равен 1∙
p(x); вероятность того, что игрок A
промахнется, равна (1—
p(x)). Ясно, что
если игрок B
еще не стрелял и знает, что игрок A больше не может выстрелить, то игрок B будет
увеличивать свои шансы на успех, выжидая, пока y не станет равным 1. Таким образом, если
игрок A
промахнется в момент x, то он
наверняка будет поражен игроком B, если x
< y.
Следовательно,
К(х,у) = 1 ∙ p(х) + (-1) ∙ (1 – p(x)) = 2p(x) – 1, если x < y .
Аналогично
L(х,у) =
(-1) ∙ q(y) +
1∙(1 – q(y)) = 1 – 2q(y), если y < x .
И функция
G(x) = 1 ∙p(x) ∙ (1- q(y)) + (-1)∙ q(y) ∙ (1
– p(x)) = p(x) – q(y) = p(x) – q(x), если x = y.

В последней формуле предполагается, что
если оба противника стреляют одновременно и с одинаковым результатом, успешным
или нет, то выигрыш равен нулю. Упрощая, мы получаем
H(x, y) = 2p(x) – 1, если 0 ≤ x < y ≤ 1;
H(x, y) = G(x) = p(x) – q(x), если x = y;
H(x, y) = 1 – 2q(y), если 0 ≤ y < x ≤ 1.
Так что ядро H(x,y) определяет игру с выбором момента
времени класса I.
Заметим, что выигрыш в точке y
= x является
средним из выигрышей, представляемых функциями K(x,x) и L(x, x). То есть G(x) = (K(x,x) + L(x, x))/2.
На рисунке 2 показаны различные случаи функции выигрыша для p(x) = q(x) = x.
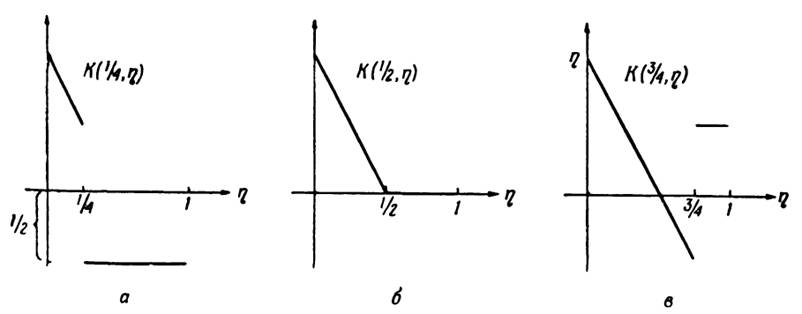
Рисунок
2. Вид функции выигрыша: (а) H(1/4, y); (б) H(1/2, y);
(в) H(3/4,
y).
Рассмотрение H(x,y) как функции от y при
определенных значениях x (см. рисунок
1) наводит на мысль, что первый игрок A будет иметь оптимальную
чистую стратегию, когда постоянная часть выигрыша, т. е. (2p(x) —1), равна
наименьшему значению выражения (1- 2q(y)) для y < x.
Это требует, чтобы
2p(x) —1 = 1 – 2q(x), (3)

Так как правая часть равенства (3)
убывает непрерывно от (+1) до (—1), когда x пробегает [0,1], а левая его часть
возрастает непрерывно от (—1) до (+1), может быть найдено хотя бы одно решение z0 уравнения (3). Заметим, что если
обе функции строго монотонны, то существует единственное решение z0.
Обозначим значение обеих частей равенства
(3) для z0 через v.
Из свойств монотонности функции H(x,y) сразу вытекает, что
H(x,y)
≥ v
≥ H(x,y0)
для всех x и y и, следовательно, что пара (x0, y0) состоит из
оптимальных стратегий.
ПРИМЕР 4.
«БОРЬБА ЗА РЫНОК СБЫТА».
Приведем здесь пример игры, которая
является некоторым видоизменением примера 3 «шумная дуэль».
Пусть имеются две фирмы, желающие
овладеть рынком сбыта с помощью вкладов. С этой целью они делают свои вклады в
определенные моменты времени по их желанию. Каждая фирма стремится сделать свой
вклад как можно позже, так как это повышает вероятность овладения рынком. С
другой стороны, каждая из них может овладеть рынком сбыта, если раньше сделает
свой вклад. Важное условие заключается в том, что, как только одна из фирм
сделает свой вклад, это становится известным. В этом случае также сразу
становится известным, овладела ли фирма рынком сбыта. Если она овладела, то
выиграла 1, а вторая выиграла 0; если она не овладела, то другая фирма, сделав
свой вклад, обязательно овладеет им и выиграет 1, а первая фирма — 0. Если
фирмы одновременно делают вклады, то каждая из них может получить рынок сбыта с
определенной вероятностью. Вообще говоря, возможны варианты исходов, когда обе
фирмы сделали вклад, и ни одна не
овладела рынком сбыта или обе фирмы овладели рынком сбыта, такие исходы
считаются ничейными, т. е. каждая фирма получает выигрыш, равный нулю. Пусть
по-прежнему [0, 1] — интервал времени, в течение которого фирмы могут делать вклады: х
означает момент, когда первая фирма делает вклад (0 ≤ х ≤ 1); у —
момент вклада второй фирмы (0 ≤ у ≤ 1); p(x)
— вероятность овладения рынком сбыта первой фирмой, если она делает свой
вклад в момент х; q(у)
— вероятность овладения рынком сбыта второй фирмой, если она делает свой вклад
в момент у.

Очевидно, значения функций p(x) и q(y)
увеличиваются с увеличением аргументов, так как вероятность овладения рынком
сбыта увеличивается с увеличением времени от начала до момента вклада. Функция
выигрышей H(х,у)
первой фирмы (игрока) формируется следующим образом.
1.
Пусть х > у. Тогда выигрыш первой фирмы будет с вероятностью р(х), а
проигрыш — с вероятностью (1 — р(х)) и
K(x,y) = 1∙ p (х) + (— 1)∙ (1 — p(x)) = 2p(x) — 1.
2. Пусть х = у.
В этом случае вероятность того, что
первая фирма выиграет, а вторая проиграет, равна:
р(х)∙(1 — q(у)) =
р(х)∙(1 — q(х));
вероятность того, что вторая фирма
выиграет, а первая проиграет, равна:
q(у)∙(1 — p(х)) = q(x)∙(1 — p(х)).
То есть
G(х) = 1 ∙ (р(х)(1 — q(х))) + (-1)
∙(q(x)(1 — p(х))) = p(x) – q(x).
3. Пусть у > х. Тогда вероятность
того, что вторая фирма выиграет, равна q(у), а вероятность того, что вторая
фирма проиграет, равна (1 — q(y)), поэтому
L(х,у)
= (—1)∙q(y) + 1∙
(1-q(y)) = 1 – 2q(у).

Таким образом, получаем игру класса I со следующим
ядром H(x,y) (функцией
выигрышей игрока A):
H(x, y) = K(x,y) = 2p(x) – 1, если 0 ≤ x < y ≤ 1;
H(x, y) = G(x) = p(x) – q(x), если x = y;
H(x, y) = L(х,у) = 1 – 2q(y), если 0 ≤ y < x ≤ 1.

Данная игра имеет решение. Функция H(х,у) имеет
седловую точку (x0,
y0).
Оптимальной стратегией фирм является делать вклады одновременно в момент t,
удовлетворяющий уравнению: p(t) + q(t) = 1. Цена
игры равна V(t) = p(t) – q(t).
Если, например, p(x) = x, q(y) = y∙у, то
оптимальное время вклада для каждой фирмы определяется из уравнения t(1+t)
=1, откуда t = 0,62. Цена игры – значение функции V (t) = t(1-t)
при t
= 0,62: V(0,62)
= 0,24. То есть первая фирма выигрывает 0,24, что и следовало ожидать, так как
на интервале [0, 1] вероятность овладения рынком сбыта у нее больше, чем у
второй фирмы.

ПРИМЕР 5. «БЕСШУМНАЯ ДУЭЛЬ».
Снова каждому из двух дуэлянтов, как и
в примере 3 «шумная дуэль», разрешается выстрелить только один раз, но в этом
случае оба пистолета снабжены глушителями, так что ни один из дуэлянтов не может
определить, выстрелил ли уже его противник или нет. Термин «бесшумная» в
противоположность «шумной» будет употребляться для того, чтобы обозначить игру,
в которой исключается какое бы то ни было знание о ходе игры, по крайней мере,
для одного из игроков. Предположим для простоты, что функции меткости заданы следующим образом: p(x) = q(x) = x. Тогда функция выигрыша H(x,y), описывающая игру, имеет следующий вид:
H(x, y) = K(x,y) = x – (1-x)y, если 0 ≤ x < y ≤ 1;
H(x, y) = G(x) = 0, если x = y;
H(x, y) = L(х,у) = (–1)∙ y + (1 – y)x, если 0 ≤ y < x ≤ 1.

Происхождение полученных соотношений для
H(x,y) аналогично
происхождению соотношений в примере 3, за исключением того, что в данном случае
ни один из игроков не может определить
момент выстрела противника, если только, разумеется, этот выстрел не оказался
успешным.
Заметим, что H(x, y) = — H(y, x); следовательно, эта бесшумная дуэль
является симметричной игрой в смысле определения, введенного в ([2], п. 10.2). Цена игры в силу
теоремы 2 равна нулю: V
= 0. И любая стратегия, которая
оптимальна для одного игрока, оптимальна также и для другого.
Полученная функция выигрыша H(x,y) определяет игру
с выбором момента времени класса II, где
K(x,y) = x – y + xy,
L(х,у) = x – y
– xy.
И частные производные имеют вид:
K’x (x,y) = 1 +y > 0, L’x
(х,у) = 1 – y > 0, 0 ≤ y < 1.
K’y (x,y) = – 1 + x <
0, L’y (х,у) = – 1 – x
< 0, 0 ≤ x
< 1.

Выражения K’x (x,y) и L’x
(х,у) означают частные производные по x; выражения
K’y
(x,y) и L’y (х,у)
означают частные производные по y. Следовательно, функции K (x,y) и L (х,у) строго возрастают по x и строго убывают по y внутри
единичного интервала (0,1).
Поскольку игроки не имеют сведений о
действиях друг друга, можно интуитивно предполагать, что в рассматриваемой игре
необходима рандомизация; естественно
также считать, что каждый игрок может выжидать весь интервал времени, чтобы
обеспечить достоверный успех. Исходя из симметрии, та же стратегия
оптимальна для игрока B
– для этого примера можно также показать, что оптимальная стратегия для каждого игрока единственна.
ПРИМЕР 6. «БОРЬБА ЗА РЫНОК СБЫТА».
В данном примере описывается игра типа
«бесшумная дуэль» из примера 5.
Две фирмы борются за рынок сбыта. Один
раз в течение определенного промежутка времени каждая из фирм должна сделать
вклад, который может привести к овладению рынком сбыта. С течением времени
сведения о конъюнктуре повышают вероятность того, что сделанный вклад приведет
к овладению рынком сбыта, поэтому каждая фирма старается сделать вклад как
можно позже, чтобы повысить вероятность овладения рынком сбыта. С другой
стороны, одна из фирм, сделавшая ранее свой вклад, может завоевать рынок сбыта,
а другая фирма потерять его, даже если
она внесет свой вклад. Пусть каждая из фирм может сделать свой вклад тайно.
Другая фирма не будет знать об этом, если фирма, сделавшая вклад, не овладеет
рынком сбыта (дуэль в таком случае считается бесшумной). Если же одна фирма
овладела рынком сбыта, то игра заканчивается выигрышем этой фирмы. Если обе
фирмы сделали вклад, и ни одна из них не
овладела рынком сбыта, то игра заканчивается вничью. Пусть рассматривается
единичный промежуток времени: х означает момент времени вклада первой фирмы, у
— момент времени вклада второй фирмы (0 ≤ х ≤ 1; 0 ≤ у
≤ 1). Пусть, далее, вероятность овладения рынком сбыта для каждой фирмы
пропорциональна времени, соответственно,
х и у, т. е. вероятность овладения рынком сбыта первым игроком,
сделавшим свой вклад в момент х, равна х (или у — для второй фирмы). Овладение
рынком сбыта оценивается величиной 1 (единица), т. е. если первая фирма
овладела рынком сбыта, то она получает 1 с вероятностью х, если не овладела, то
она получает выигрыш равный (—1) с вероятностью (1 — х). Аналогично для второй
фирмы.
Построим функцию выигрышей H(x,y) для этой
игры.
1. Пусть х < у, тогда
H(х, у) = К(х,у) = x – y + ху.
Действительно, первая фирма делает свой
вклад раньше, чем вторая, и поэтому средний ее выигрыш состоит из выигрыша
(+1) с вероятностью х, выигрыша
(—1) (проигрыша) с вероятностью у
∙ (1 — х), т. е.
К(х,у) = 1 ∙ х + (-1) ∙ (1-x)
∙у = x – y
+ ху.
2. Пусть х = у, тогда
H(х, у) = G(x) = 1∙ x ∙(1-y) + (-1) ∙(1-x) ∙y = x – y = x – x = 0.
3.
Если у < х, тогда,
по аналогии с построением функции K(x,y),
получим функцию выигрыша для первого игрока A в случае y < x:
L(x,y) = (-1) ∙ y + 1 ∙
(1-y)
∙x = x – y
– xу.
Поскольку для этой игры выполнено условие:
К(х,у) = - L(y,
x),
то цена игры
V = 0, оптимальные смешанные стратегии игроков существуют.
Решая данную игру, получаем оптимальную
стратегию первого игрока A:
0, если х <1/3; (1/(x∙4∙x))/x,
если х > 1/3,
которая указывает, что первую треть
периода не следует делать вклад, а в оставшемся периоде следует делать его с
вероятностью ((0,25/x)/x)/x.

ПРИМЕР 7. «СМЕШАННАЯ ДУЭЛЬ».
Мы предполагаем, что игрок A
имеет бесшумный пистолет, а игрок B — шумный, так что игрок A
знает, выстрелил ли игрок B или нет, а игрок B такой
информации не имеет. Функции меткости снова принимаются равными: p(x)=q(x)=x. Тогда
функция выигрышей игрока A
имеет вид:
H(x, y) = K(x,y) = x – y + xy, если 0 ≤ x < y ≤ 1;
H(x, y) = G(x) = 0, если x = y;
H(x, y) = L(х,у) = 1 – 2y, если 0 ≤ y < x ≤ 1.

Сопоставим решение смешанной дуэли и
решение полностью бесшумной дуэли (см.: [2]).
Прежде всего, мы заметим, что в бесшумной дуэли спектр начинается в а=1/3, в то
время как в смешанной дуэли спектр начинается в а=(√6 — 2)>1/3.
Другими словами, когда один из игроков имеет преимущество в возможности слышать
выстрел своего противника, его оптимальная стратегия требует для выстрела более
позднего момента времени, чем при обычных обстоятельствах бесшумной дуэли.
Второе и самое интересное отличие в решении смешанной дуэли состоит в том, что
игрок B
(игрок с шумным оружием) должен сохранять угрозу выстрела до самого конца. Это отражено
в скачке при y = 1. На самом деле такое поведение игрока
B
не должно казаться странным ввиду неравенства информации, имеющейся в
распоряжении каждого из игроков.
РАЗДЕЛ 3. ИГРЫ С ИЗВЕСТНЫМИ
ПРОСТРАНСТВАМИ СТРАТЕГИЙ.
Реальные конфликтные ситуации приводят
к разным видам игр. Различны и способы их анализа и разрешения. В двух
предыдущих разделах лекции мы рассматривали различные классы игр, определенных на единичном квадрате, для
которых пространства стратегий X и Y
отождествлялись с множеством вероятностных
распределений на единичном интервале. В этом разделе мы приведем несколько типичных примеров игр, в которых
пространствами стратегий являются подмножества известных функциональных
пространств, но которые нельзя рассматривать, как игры, разыгрываемые на единичном квадрате.
ПРИМЕР 8. «ДУЭЛЬ СНАЙПЕРА С ПУЛЕМЕТЧИКОМ».
Снайпер С, располагающий одним
выстрелом, стремится уничтожить пулеметчика П. Так как С может выстрелить
только один раз, его стратегия состоит в выборе момента времени для этого
выстрела. Пусть a(t) — меткость
снайпера, т. е. вероятность того, что П будет уничтожен, если С стреляет в момент (или на расстоянии) t
(переменная t нормирована так, что она изменяется в сегменте [0, 1]). Смешанной
стратегией С (1-й игрок) является вероятностное распределение на [0, 1]. В этой
модели мы предполагаем, что как только С выстрелил, успешно или нет, он сразу
же скрывается (если он в состоянии это сделать), и дуэль заканчивается.
Пулеметчик вооружен пулеметом и, защищаясь, пытается уничтожить снайпера. Стратегия П определяется
функцией p(t), измеряющей интенсивность,
с которой стреляют из пулемета в момент t. Мы предполагаем, что боеприпасы П,
если он стреляет с максимальной
плотностью, иссякнут за период δ < 1. Следовательно, нерандомизированные стратегии p(t) для П
состоят из всех функций, удовлетворяющих ограничениям:
0
≤ p(t)≤ 1;
1
∫ p(t)dt = δ < 1. (4)
0

Меткость пулеметчика r(t) непрерывна
и монотонна, причем r(0)
= 0, r(1)=1.
Функция r(t) измеряет
меткость в том смысле, что если П стреляет с интенсивностью p(t) в течение
малого интервала времени [t,
t+h], то
вероятность того, что С будет уничтожен, равна:
p(t)∙r(t)∙h + o(h).
Предположим, что φ(t, p) —
вероятность того, что С выживет к тому моменту t, когда П решил стрелять с
интенсивностью p(t).

Ясно, что для малых положительных h имеем:
φ(t+h, p)= φ(t, p)∙[1 – p(t)∙r(t)∙h] + o(h).
Функция выигрыша H(x, p) для этой игры, когда С применяет чистую стратегию x (момент
единственного выстрела), а П применяет
стратегию y,
вычисляется следующим образом. Положим выигрыш С равным α, если С
уничтожает П, (– β), если П уничтожает С, и нулю, если ни один из
противников не уничтожен. Тогда ядро H(x, p), рассматриваемое как ожидаемый выигрыш С
(игрока A),
равно:
H(x, p) = α∙a(x)∙φ(x, p) – β∙(1 –
φ(x,
p)).
(5)
Выигрыш игрока A (снайпер С) в условиях его смешанной
стратегии ξ и выбора р игроком B (пулеметчик
П) получается усреднением (5) относительно меры ξ(x):
1
H(ξ, p) = ∫ H(x, p) dξ(x). (6)
0

Итак, мы можем рассматривать эту игру
как тройку (X, Y,
H), где X—пространство вероятностных
распределений на единичном интервале, Y состоит из всех р, удовлетворяющих (4),
а H
вычисляется по формуле (6). Формальное различие между этой игрой и обычной
игрой на единичном квадрате очевидно.
Пространство стратегий Y
в этом случае имеет иной характер и требует новых методов анализа. Для определения вида оптимальной стратегии игрока
A
(снайпер С) можно использовать классическую лемму Неймана — Пирсона (см.: [2],
п. 16.4), являющуюся фундаментальной теоремой статистики. Применение леммы
Неймана — Пирсона в данном случае является естественным ввиду ограничений (4). Решение данной игры
приводится в главе 16 монографии [2].
ПРИМЕР 9. «РЕКЛАМНАЯ БОРЬБА».
В этом примере мы приведем некоторую
интерпретацию игры, сформулированной в примере 8, которая описывает дуэль между
снайпером, способным выстрелить лишь один раз, и пулеметчиком, способным вести
непрерывный огонь. Мы будем рассматривать здесь небольшое видоизменение этой задачи,
которую мы будем интерпретировать как рекламную борьбу. Основные черты решений
этих двух задач совпадают. Модель может полностью и не соответствовать встречающейся
в жизни ситуации, но она указывает, какого типа разумные рекомендации,
касающиеся поведения участников этой ситуации, вытекают из анализа игровых задач.
Рассмотрим конкуренцию между двумя
дельцами, мистером К (Крупный) и мистером М (Мелкий). К процветает и имеет устойчивый круг клиентов; М находится на краю
банкротства. В некоторый момент t= 0 на сцену появляется потенциальный заказчик. Он может решить
не покупать вообще, но если уж покупает, то одному из концернов (и притом
только одному) будет сделан большой заказ. Заказ этот достаточно велик, чтобы
поставить М на ноги, однако, чтобы не вылететь в трубу еще до заключения
контракта, М должен получить заказ до определенного времени (назовем его временем
t=1).
В момент t=
0 дельцы К и М вступают в рекламную борьбу. Так как M, несомненно, будет вынужден бросить
дело, если он не обеспечит себе этот заказ, то К будет рассматривать как победу
даже такую ситуацию, когда покупатель решит не покупать вовсе. М выигрывает, если он обеспечивает себе
заказчика в нужный срок, К выигрывает,
если заказчик не покупает вообще или если заказ получает K. При
надлежащей интерпретации характеристик полезности участников игра имеет нулевую сумму. Мы
предполагаем здесь, что только К или М могут получить заказ и что именно реклама
будет решающим фактором, определяющим
решение заказчика. Отметим следующее обстоятельство: преимуществом К является возможность
распространить свою рекламную
деятельность на весь период, в то время как для М лучше всего сконцентрировать
свои ресурсы на одном продуманном мероприятии.
Каждый должен, исходя из своих целей и возможностей, решить, когда заниматься
рекламой.
Мы предполагаем, что сопротивление
потребителя рекламе убывает со временем.
Кроме того, мы предполагаем, что психология заказчика такова, что все предыдущие
рекламы, которые уже появились, не оказывают на него влияния, когда он читает
данную рекламу. Мы сформулируем теперь кампанию, как математически непрерывный процесс. М выбирает для
осуществления рекламы момент времени t из [0,1], а К выбирает темпы
расходования средств, которые подчинены следующим ограничениям:
0 ≤ p(t)≤ 1;
1
∫ p(t)dt = δ < 1.
0

где δ соответствует деньгам,
ассигнованным дельцом К на рекламную
кампанию (другими словами, если К расходует деньги с максимальной скоростью, то они будут
израсходованы в течение времени δ).
Пусть a(t)— вероятность успеха M,
если он рекламирует в момент времени t; r(t) представляет
вероятность того, что вложение одного доллара в момент времени t обеспечит заказ для К, если он до того времени
еще не будет размещен.
Говоря более точно, r(t)∙ p(t) есть плотность вероятности, соответствующая скорости
расходов p(t).
Как уже отмечено, мы предполагаем, что
как r(t),
так и a(t)
со временем возрастают. Для фиксированных стратегий, момента t для игрока М и
скорости расходов p(t) для игрока К
вероятность выигрыша игрока М равна вероятности того, что заказчик будет
сопротивляться дельцу К до момента t, а
затем уступит игроку М. Пусть φ(t, p) — вероятность сопротивления заказчика
рекламе дельца K в течение интервала [0, t]. Когда К
(игрок B)
использует стратегию p(t), а М (игрок A) действует в момент t, функция выигрыша H(t, p(t)) равна:
H(t, p(t)) = α∙a(x)∙φ(t, p(t)) – β∙(1 – φ(t, p(t))),
где α — выигрыш M, если M
выигрывает заказ, a β — выигрыш дельца К, если М становится банкротом.
Коэффициенты при этих выигрышах, очевидно, равны вероятностям соответствующих
событий в условиях выбора стратегий t для М и p(t) для K.

Выигрыш игрока A (коммерсант М) в условиях его
смешанной стратегии ξ и выбора р
игроком B
(делец K)
получается усреднением (5) относительно меры ξ(t) на пространстве чистых стратегий:
1
H(ξ, p) = ∫ H(t, p) dξ(t).
0

Решение данной игры приводится в главе
16 монографии [2].
ПРИМЕР 10. ДИФФЕРЕНЦИАЛЬНАЯ ИГРА ПОИСКА.
Ищущий (игрок А) стремится обнаружить
уклоняющегося (игрока В). Оба игрока
перемещаются с постоянными скалярными
скоростями (α и β соответственно) по плоскости внутри
некоторой поисковой области Ω. В любой момент времени каждый из игроков управляет своим перемещением, задавая
направление вектора скорости. Пусть (xA, yA)
и (xВ,
yB)
– координаты игроков. Тогда имеем
dxA/dt = α cos(φ),
dyA/dt = α sin(φ),
dxB/dt = β cos(ψ),
dyB/dt = β sin(ψ).
Игра поиска заканчивается в тот момент,
когда игроки сблизятся на расстояние L > 0,
иными словами, когда будет выполнено неравенство
(xA – хB)2 + (уА – yB)2
< L2.

В случае успешного обнаружения выигрыш
игрока A
считается равным 1. Построение решения в этой игре существенно зависит от характера и степени информированности
игроков.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Данилов В.И. Лекции по теории игр. М.: Российская
экономическая школа, 2001.
[2] С.
Карлин. Математические методы в теории
игр, программировании и экономике. Издательство «Мир», Москва, 1964.

[3] Печерский С.Л., Беляева А.А. Теория игр для экономистов.
Вводный курс. Учебное пособие. СПб.: 2001.
[4] Фомин
Г.П. Математические методы и модели в коммерческой деятельности: Учебник. —
2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.
[5] Шикин Е.
В. От игр к играм. Математическое введение. Изд. 2-е, исправл. — М.: Едиториал
УРСС, 2003. — 112 с.
