Теория игр. Игры с природой. Оптимальная стратегия. Максиминный критерий Вальда. Критерий минимаксного риска Сэвиджа. Критерий Гермейера. Максимаксный критерий. Критерий Байеса. Вероятности состояний природы. Колебание выигрышей игрока. Риск игрока. Критерий Лапласа. Критерий недостаточного основания Лапласа
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Контрольные
вопросы
к
лекции № 5 ««Игры с природой»
по
предмету
«Теория
игр»

1.
Риском ИГРОКА при применении им стратегии Аi и при состоянии природы Qj называется:
А)
разность между выигрышем ИГРОКА при применении им стратегии Ai и при
состоянии природы Qj
и минимальным выигрыш ИГРОКА при состоянии природы Qj;
Б)
разность между максимальным выигрышем ИГРОКА при применении им стратегии Ai и выигрышем ИГРОКА при применении им
стратегии Аi
и при состоянии природы Qj;
В) разность между максимальным
выигрышем ИГРОКА при состоянии природы Qj и выигрышем ИГРОКА при применении им
стратегии Аi
и при состоянии природы Qj.
2.
Колебанием выигрышей ИГРОКА при состоянии природы Qj называется:
А) разность между максимальным и минимальным
выигрышами ИГРОКА при состоянии природы Qj;
Б)
сумма максимального и минимального выигрышей ИГРОКА при состоянии природы Qj;
В)
произведение максимального и минимального выигрышей ИГРОКА при состоянии
природы Qj.
3.
Показателем благоприятности состояния природы Qj называется:
А)
минимальный выигрыш ИГРОКА при состоянии природы Qj;
Б) максимальный выигрыш ИГРОКА при
состоянии природы Qj;
В)
сумма максимального и минимального выигрышей ИГРОКА при состоянии природы Qj.
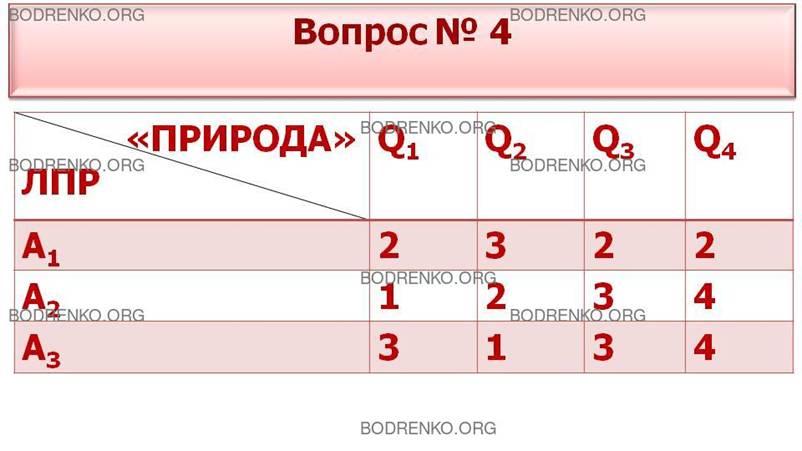
4.
Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по
максиминному критерию Вальда.
|
2 |
3 |
2 |
2 |
|
1 |
2 |
3 |
4 |
|
3 |
1 |
3 |
4 |
A =
A) A1;
Б) A2;
В) A3.
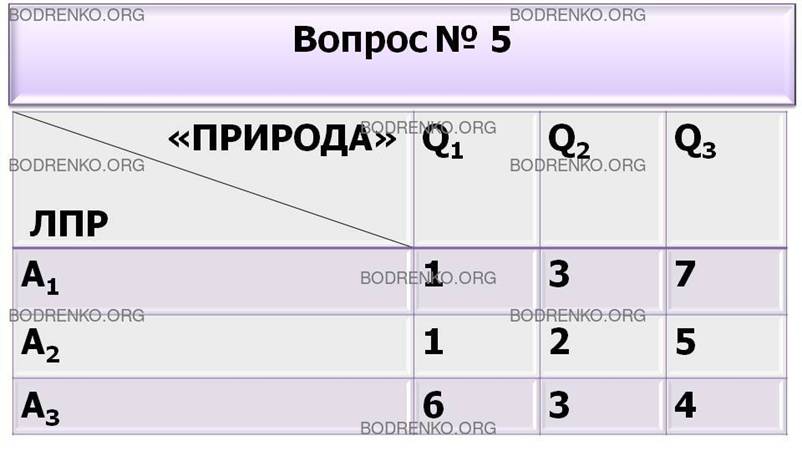
5.
Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по критерию
минимаксного риска Сэвиджа.
|
1 |
3 |
7 |
|
1 |
2 |
5 |
|
6 |
3 |
4 |
A =
A) A1;
Б) A2;
В) A3.
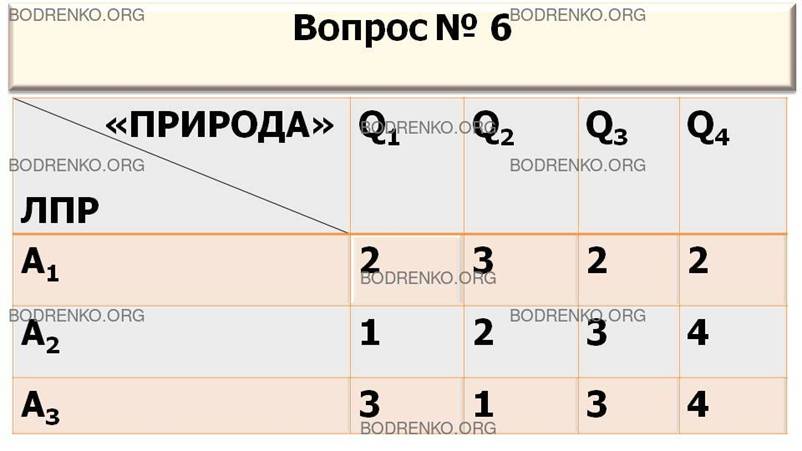
6. Игра с природой задана платежной матрицей A. Найти
оптимальную стратегию по критерию Лапласа
относительно выигрышей (критерий «недостаточного основания» Лапласа).
|
2 |
3 |
2 |
2 |
|
1 |
2 |
3 |
4 |
|
3 |
1 |
3 |
4 |
A=
A) A1;
Б) A2;
В) A3.
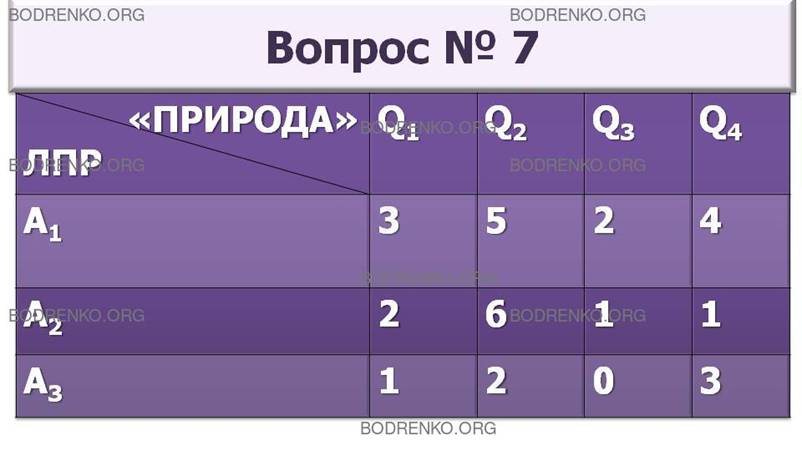
7.
Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по
критерию Лапласа
относительно рисков.
|
3 |
5 |
2 |
4 |
|
2 |
6 |
1 |
1 |
|
1 |
2 |
0 |
3 |
A =
A) A1;
Б) A2;
В) A3.
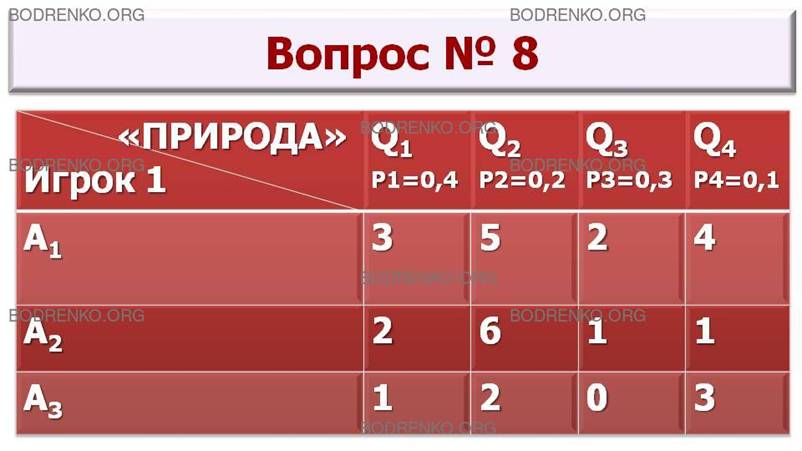
8.
Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по
критерию Гермейера с
учетом вероятностей состояний «природы»: P1=0,4; P2=0,2; P3=0,3; P4=0,1.
A =
|
3 |
5 |
2 |
4 |
|
2 |
6 |
1 |
1 |
|
1 |
2 |
0 |
3 |
A) А1;
Б)
А2;
В)
А3.
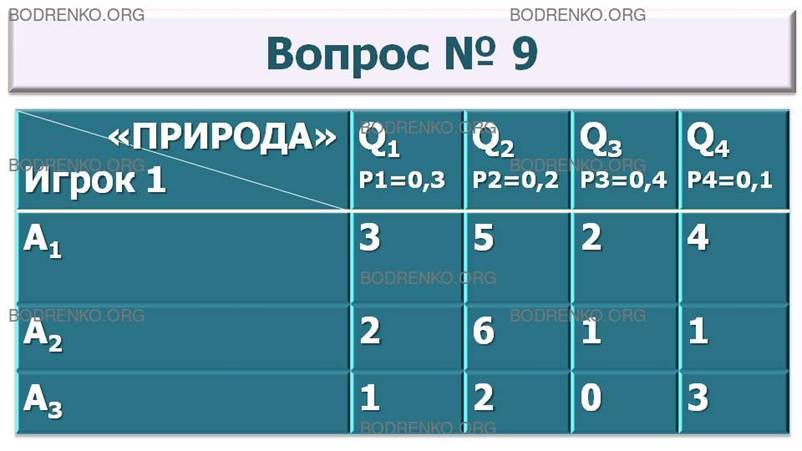
9.
Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по максимаксному критерию с учетом вероятностей состояний
«природы»: P1=0,3;
P2=0,2;
P3=0,4;
P4=0,1.
A =
|
3 |
5 |
2 |
4 |
|
2 |
6 |
1 |
1 |
|
1 |
2 |
0 |
3 |
A)
А1;
Б) А2;
В)
А3.
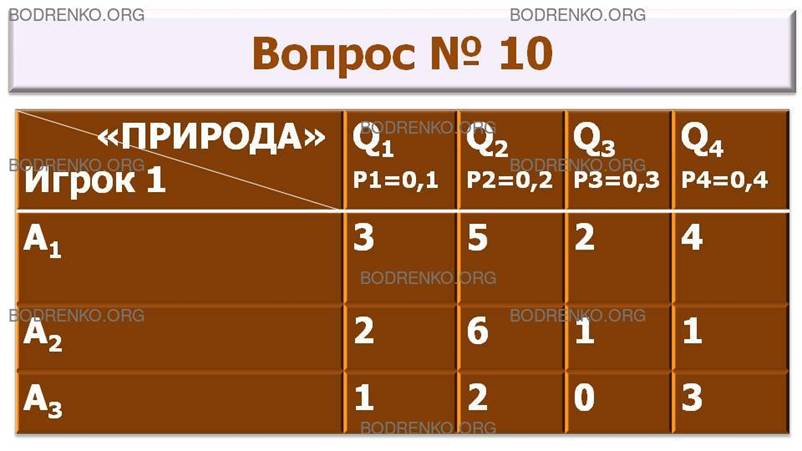
10.
Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по критерию Байеса относительно выигрышей
(критерий максимума ожидаемого среднего выигрыша). Вероятности состояний
«природы» следующие: P1=0,1;
P2=0,2;
P3=0,3;
P4=0,4.
A =
|
3 |
5 |
2 |
4 |
|
2 |
6 |
1 |
1 |
|
1 |
2 |
0 |
3 |
A) А1;
Б) А2;
В) А3.