Теория игр. Игры с природой. Понятие игры с природой. Критерии выбора оптимальных решений в условиях полной неопределенности. Критерии выбора оптимальных решений в условиях риска. Максиминный критерий Вальда. Критерий максимакса. Критерий пессимизма-оптимизма Гурвица. Критерий минимаксного риска Сэвиджа
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Теория игр
Лекция 5
Тема лекции 5: «Игры с природой»

Разделы лекции:
1.
Понятие игры с природой.
2.
Критерии выбора оптимальных решений в условиях полной неопределенности.
3.
Критерии выбора оптимальных решений в условиях риска.

РАЗДЕЛ 1. ПОНЯТИЕ ИГРЫ С ПРИРОДОЙ.
Математическая теория игр дает научно обоснованные
рекомендации поведения в конфликтных ситуациях, показывая «как играть, чтобы не
проиграть». Для применения этой теории необходимо уметь представлять конфликты
в виде игр. Характерной особенностью
любого конфликта является то, что ни одна из участвующих сторон не знает
заранее точно и полностью всех своих возможных решений, а также и другие
стороны, их будущее поведение и, следовательно, каждый вынужден действовать в
условиях неопределенности. Неопределенность исхода может быть обусловлена как
сознательными действиями активных противников, так и несознательными,
пассивными проявлениями, например, стихийных сил природы: дождя, солнца, ветра,
лавины и т.п. В таких случаях исключается возможность точного предсказания
исхода. В одних конфликтах
противоположной стороной выступает сознательно и целенаправленно действующий
активный противник, заинтересованный в нашем поражении, который сознательно
препятствует успеху, добивается победы любыми средствами. В других конфликтах
такого сознательного противника нет, а действуют лишь так называемые «слепые
силы природы»: погодные условия, состояние торгового оборудования на
предприятии, болезни сотрудников, нестабильность
экономической ситуации, рыночная конъюнктура, динамика курсов валют, уровень
инфляции, налоговая политика, изменяющийся покупательский спрос и т.п. В таких случаях
природа не злонамеренна и выступает пассивно, причем иногда во вред человеку, а
иногда к его выгоде, однако ее состояние и проявление могут ощутимо влиять на
результат деятельности. То есть в задачах подобного рода выбор
решения зависит от состояний объективной экономической действительности,
называемой в модели «ПРИРОДОЙ». Термин «ПРИРОДА» характеризует некую
объективную действительность, которую не следует понимать буквально. Математические
модели подобных конфликтных ситуаций
называются «ИГРАМИ С ПРИРОДОЙ». В таких играх человек старается действовать
осмотрительно, например, используя стратегию, позволяющую получить наименьший
проигрыш. Второй игрок (природа) действует незлонамеренно, совершенно случайно, возможные стратегии его
известны (стратегии природы). Такие ситуации исследуются с помощью теории
статистических решений. Хотя
вполне могут встречаться ситуации, в которых игроком может действительно
выступать природа. Например, обстоятельства, связанные с погодными
условиями или с природными
стихийными силами. Игра
человека с природой тоже отражает конфликтную ситуацию, возникающую при
столкновении интересов в выборе решения. Но «стихийным силам природы» нельзя
приписать разумные действия, направленные против человека и тем более какой-либо «злой умысел». Таким
образом, корректнее говорить о конфликтной ситуации, вызванной столкновением
интересов человека и неопределенностью действий природы, но без явной
антагонистической окраски. Ситуации, в которых риск связан не
с сознательным противодействием противоположной стороны (среды), а с
недостаточной осведомленностью о ее поведении или состоянии лица, принимающего
решение, исследуются с помощью теории
статистических решений. Создателем теории статистических игр считается
А. Вальд. Он показал, что в теории принятия решений статистические игры
являются основным подходом, если решение принимается в условиях риска.
КАКОВЫ
ОСНОВНЫЕ ОТЛИЧИЯ СТАТИСТИЧЕСКОЙ ИГРЫ ОТ МАТРИЧНОЙ ИГРЫ?
Статистическая
игра существенно отличается от конечной антагонистической игры двух лиц с
нулевой суммой, где выигрыш одного равен проигрышу другого (то есть матричной
игры). В статистической игре «ПРИРОДА» не является разумным игроком, который
стремится выбрать для себя оптимальные стратегии. Этот игрок не заинтересован в
выигрыше. Другое дело – человек, в данном случае, статистик. Он имеет целью
выиграть игру с воображаемым противником, т. е. с ПРИРОДОЙ. Игрок-ПРИРОДА не
выбирает оптимальной стратегии, но статистик должен стремиться к определению
распределения вероятностей состояния природы.
Основными отличиями статистической игры от стратегической являются:
- отсутствие
стремления к выигрышу у игрока-ПРИРОДЫ, т. е. отсутствие антагонистического
противника;
- возможность игрока-статистика провести статистический
эксперимент для получения дополнительной информации о стратегиях природы.
Так, например, статистик, работающий в фирме
«Одежда», может изучить многолетние данные о погодных условиях в местностях,
где одежда будет продаваться, и в зависимости от наиболее вероятного состояния
погоды выработать рекомендации, куда и какое количество партий изделий
отправлять, где выгоднее и на каком уровне провести сезонное снижение цен и т.
д.
Таким
образом, теория статистических решений является теорией проведения
статистических наблюдений, обработки этих наблюдений и их использования. Для
принятия решений в условиях риска используют методы теории вероятностей, если
это возможно, по причине массовости явления. В таком случае факторы, например,
состояния среды, представляют собой либо
случайные величины, либо случайные функции. Они описываются какими-либо
статистическими характеристиками, например математическим ожиданием и
дисперсией, и обладают статистической устойчивостью.
В игре
«с природой» участвуют два игрока.
Игрок 1
– это лицо, принимающее решение (ЛПР), обозначим его «А».
Игрок 2
– это «ПРИРОДА», обозначим его «Q».
В играх
«с природой» сознательно действует только один из участников – лицо, принимающее решение (ЛПР). «ПРИРОДА» является вторым игроком, но не
противником игрока А. Так как «ПРИРОДА» осознанно против первого игрока не
действует, принимает то или иное свое состояние определенным образом,
конкретных целей в игре не преследует и безразлична к результату игры. То есть «ПРИРОДА», являясь игроком в игре «с
природой», не является ни противником, ни союзником игрока А.
КАК СТРОИТСЯ
МАТРИЦА ВЫИГРЫШЕЙ В ИГРЕ С ПРИРОДОЙ?
Формально
изучение игр «с природой», так же как и стратегических, должно начинаться с
построения матрицы выигрышей (платежной матрицы), что является, по существу,
наиболее трудоемким этапом подготовки принятия решения. Ошибки, допущенные при
формировании матрицы выигрышей (платежной матрицы), не могут быть
компенсированы никакими вычислительными методами и приведут к неверному
итоговому результату. Матрица игры «с
природой» аналогична платежной матрице стратегической игры «m x n» (рисунок 1). Формализация задачи происходит следующим
образом: у активного игрока (человека) возможные действия по-прежнему
называются стратегиями, а возможные действия пассивного игрока (природы) –
состояниями или условиями природы. Пусть игрок 1 – «A» (лицо, принимающее
решение), имеет m стратегий Ai, i = 1, …, m. Игрок 2 – «ПРИРОДА», может находиться в одном из n возможных состояний Qj, j = 1, …, n. Состояния природы Qj можно рассматривать как ее
возможные «стратегии». Обычно
предполагается, что игрок A
(ЛПР) в состоянии оценить результаты выбора им каждой из своих стратегий Ai, i=1,…,m, при каждом состоянии природы Qj, j=1,…,n. Эти результаты
количественно выражаются действительными числами aij,
и называются выигрышами игрока A
(ЛПР) в игре «с природой». Так как в
играх «с природой» в качестве первого игрока всегда выступает человек (ЛПР), то
можно составить матрицу выигрышей (платежную матрицу) игры «с природой» –
матрицу размера «m
x
n»
с элементами {aij}. Номер строки матрицы соответствует номеру
стратегии, применяемой первым игроком – человеком (ЛПР). Номер столбца соответствует номеру
состояния «ПРИРОДЫ» – второго игрока. Элемент матрицы aij – это выигрыш игрока 1 (ЛПР), если он выбрал
стратегию Ai
при состоянии природы Qj.
В ЧЕМ ЗАКЛЮЧАЕТСЯ
СОДЕРЖАТЕЛЬНОЕ ОТЛИЧИЕ МАТРИЦЫ ВЫИГРЫШЕЙ В ИГРЕ С ПРИРОДОЙ ОТ ПЛАТЕЖНОЙ МАТРИЦЫ
КОНЕЧНОЙ АНТАГОНИСТИЧЕСКОЙ ИГРЫ?
Содержательное
отличие матрицы выигрышей в игре «с природой» от платежной матрицы
конечной антагонистической
игры заключается в том, что элементы столбцов этой матрицы не являются
проигрышами «природы» при соответствующих ее состояниях. Выигрыши aij платит, естественно, не
«ПРИРОДА», а некая третья сторона или совокупность сторон, влияющих на принятие
решения игроком 1, и объединенных в понятие «ПРИРОДА».

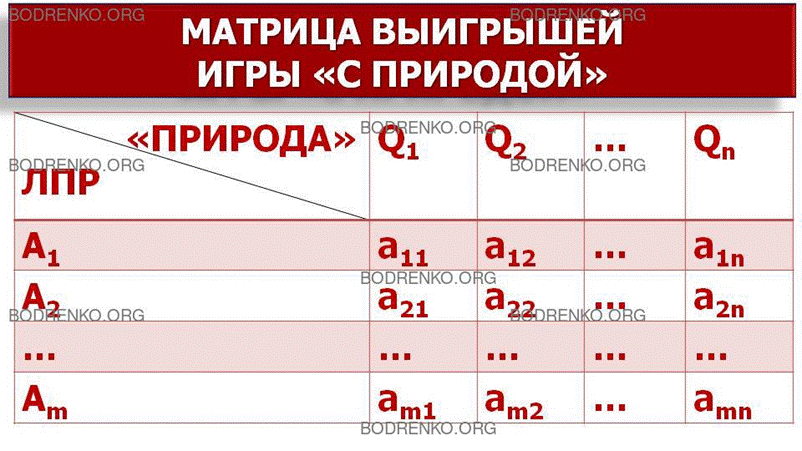
Рисунок 1. Матрица игры «с природой» (матрица выигрышей).
Если в
распоряжении игрока A
всего одна стратегия A1,
то есть m =1, то проблема выбора им
оптимальной стратегии отпадает. Поэтому в дальнейшем целесообразно считать m ≥ 2. Если «ПРИРОДА» Q может пребывать только в одном
состоянии Q1,
то есть n
=1, то проблема выбора игроком A
оптимальной стратегии превращается в тривиальную: игрок A
должен выбрать стратегию Ak
такую, что выигрыши аk1
≥ ai1, i=1,…, m. Поэтому будем предполагать, что
n
≥ 2.
МОЖНО ЛИ
ДОМИНИРОВАТЬ СТРАТЕГИИ В ИГРЕ С
ПРИРОДОЙ?
В игре с
природой можно также доминировать стратегии.
Если k-я
строка матрицы A
доминируется (в частности, дублируется) какой-либо другой s-й строкой этой матрицы (k≠s), то есть, если выполнены неравенства: akj ≤ asj, для всех j=1, ..., n,
(в частности, выполнены равенства: akj = asj, j = 1,…, n). То доминируемую (в частности,
дублируемую) k-ю
строку матрицы A
можно удалить, как строку, определяющую стратегию Ak,
заведомо не лучшую стратегии As.
В результате матрица A
упрощается за счет уменьшения числа строк.
ПРИМЕР 1.
(ДОМИНИРОВАНИЕ СТРАТЕГИЙ В ИГРЕ С ПРИРОДОЙ).
Рассмотрим
пример матрицы выигрышей в игре «с природой» (рисунок 2).
|
Состояния
«ПРИРОДЫ» Стратегии ЛПР |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
|
A1 |
3 |
5 |
3 |
3 |
1 |
|
A2 |
8 |
5 |
6 |
1 |
3 |
|
A3 |
4 |
3 |
2 |
4 |
1 |
|
A4 |
3 |
9 |
3 |
0 |
2 |
|
A5 |
4 |
7 |
4 |
8 |
1 |

Рисунок 2.
Доминирование стратегий в игре «с природой».
В данном
примере стратегия A5 доминирует стратегии A1 и А3, поэтому строки,
соответствующие стратегиям A1 и A3, можно вычеркнуть. Число строк в
полученной матрице – на 2 меньше, чем в исходной матрице. Размер матрицы игры
будет равен «3x5»
(рисунок 3).
|
Состояния
«ПРИРОДЫ» Стратегии ЛПР |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
|
A2 |
8 |
5 |
6 |
1 |
3 |
|
A4 |
3 |
9 |
3 |
0 |
2 |
|
A5 |
4 |
7 |
4 |
8 |
1 |

Рисунок 3.
Доминирование стратегий в игре «с природой».
Таким
образом, в играх «с природой» можно и нужно пользоваться принципом
доминирования стратегий игрока A
(игрока – ЛПР). Но доминирование
стратегий в игре с природой имеет определенную специфику.
В ЧЕМ ЗАКЛЮЧАЮТСЯ
ОСОБЕННОСТИ ДОМИНИРОВАНИЯ СТРАТЕГИЙ В ИГРЕ С ПРИРОДОЙ?
Исключать из рассмотрения можно
лишь доминируемые стратегии игрока A (ЛПР). А
столбцы, отвечающие состояниям «ПРИРОДЫ», вычеркивать из матрицы игры
недопустимо. Поскольку «ПРИРОДА» не стремится
к выигрышу в «игре» с человеком, для нее нет целенаправленно выигрышных или
проигрышных состояний (стратегий). «ПРИРОДА» действует неосознанно. Например, в полученной матрице (рисунок 3)
пятый столбец (Q5)
доминирует первый, второй и третий столбцы (Q1, Q2, Q3). Поэтому в матричной игре эти
столбцы можно было бы удалить. Но в игре «с природой» этого делать нельзя. Это
обстоятельство является еще одним свойством, отличающим игры «с природой» от
матричных игр.
Таким
образом, в дальнейшем будем считать, что матрица выигрышей (рисунок 1) не
содержит доминируемых (в частности, дублируемых) строк.
ОТ ЧЕГО ЗАВИСЯТ
МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В ИГРАХ С ПРИРОДОЙ?
Методы
принятия решений в играх «с природой» зависят от того, известны или нет вероятности состояний (стратегий) «ПРИРОДЫ» Q.
СЛУЧАЙ 1.
Пусть
события, состоящие в том, что «ПРИРОДА» Q находится в одном из своих
состояний Q1,
…, Qn, несовместны
и составляют полную группу событий.
При этом вероятности pj
состояний «ПРИРОДЫ» Qj
известны, то есть известны значения:
p1 = p(Q1), p2 = p(Q2), …, pn = p(Qn),
где
выполнены условия:
pj
> 0, j=1,
…, n;
∑pj
= 1. (*)

В этом
случае имеет место ситуация риска, и решения
принимаются в условиях риска. Принятие решений в условиях риска
характеризуется тем, что поведение природы (среды) Q имеет случайный характер. Это
проявляется в том, что существует некоторая вероятностная мера, в соответствии
с которой возникают (наступают) те или иные состояния Qj природы Q. При этом лицо, принимающее
решение, имеет определенную информацию о вероятностях появления состояний Qj «ПРИРОДЫ», которая по своему
характеру может быть весьма разнообразна. Например, если имеются три состояния
«ПРИРОДЫ» Q1, Q2 и Q3, то дополнительная информация о появлении этих состояний
может заключаться в том, что состояние Q1 наименее вероятно, а состояние Q3
наиболее вероятно. Статистические модели
принятия решений представляют собой игру двух лиц (человека и природы) с
использованием человеком дополнительной статистической информации о состояниях
природы.
СЛУЧАЙ 2.
Если вероятности, с которыми «ПРИРОДА» Q может находиться в том или ином
своем состоянии, неизвестны и отсутствует возможность
получения о них какой-либо статистической информации, то имеет место ситуация
полной неопределенности, и решения
принимаются в условиях полной неопределенности.
Цель в играх «с природой»: независимо от вида матрицы игры требуется выбрать такую стратегию игрока A (ЛПР), которая была бы наиболее выгодной по сравнению с другими.
РАЗДЕЛ 2. КРИТЕРИИ ВЫБОРА ОПТИМАЛЬНЫХ РЕШЕНИЙ В
УСЛОВИЯХ ПОЛНОЙ НЕОПРЕДЕЛЕННОСТИ.
Рассмотрим игру «с природой», в которой вероятности pj состояний природы Qj неизвестны, и отсутствует всякая возможность получения о них какой-либо статистической информации. То есть мы находимся в состоянии полной неопределенности, связанной с отсутствием информации о вероятностях состояний природы. Неопределенность, связанную с отсутствием информации о вероятностях состояний среды (природы), называют «безнадежной» или «дурной». В случаях неопределенности такого вида («безнадежной» неопределенности) для выбора наилучших решений в играх «с природой» применяются следующие классические критерии.
КАКОВЫ КРИТЕРИИ
ВЫБОРА ОПТИМАЛЬНЫХ РЕШЕНИЙ В УСЛОВИЯХ ПОЛНОЙ НЕОПРЕДЕЛЕННОСТИ?
Первая
группа критериев – это КРИТЕРИИ ВЫБОРА ОПТИМАЛЬНЫХ РЕШЕНИЙ относительно
выигрышей. Здесь мы рассмотрим
следующие критерии.
1.
МАКСИМИННЫЙ КРИТЕРИЙ ВАЛЬДА (КРИТЕРИЙ ГАРАНТИРОВАННОГО РЕЗУЛЬТАТА).
2.
КРИТЕРИЙ МАКСИМАКСА (КРИТЕРИЙ КРАЙНЕГО ОПТИМИЗМА).
3.
КРИТЕРИЙ ПРОИЗВЕДЕНИЙ В УСЛОВИЯХ ПОЛНОЙ НЕОПРЕДЕЛЕННОСТИ.
4.
КРИТЕРИЙ ПЕССИМИЗМА-ОПТИМИЗМА ГУРВИЦА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С ПОКАЗАТЕЛЕМ
ОПТИМИЗМА λ.
5.
ОБОЩЕННЫЙ КРИТЕРИЙ ПЕССИМИЗМА-ОПТИМИЗМА ГУРВИЦА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С
КОЭФФИЦИЕНТАМИ λ1, λ2, …, λn
(КРИТЕРИЙ ОБОБЩЕННОГО МАКСИМИНА ГУРВИЦА).
Вторая
группа критериев – это КРИТЕРИИ ВЫБОРА ОПТИМАЛЬНЫХ РЕШЕНИЙ относительно рисков. К ним относятся следующие критерии.
1.
КРИТЕРИЙ МИНИМАКСНОГО РИСКА СЭВИДЖА.
2.
КРИТЕРИЙ ПЕССИМИЗМА-ОПТИМИЗМА ГУРВИЦА ОТНОСИТЕЛЬНО РИСКОВ.
МАКСИМИННЫЙ
КРИТЕРИЙ ВАЛЬДА.
При
применении данного критерия «ПРИРОДА» рассматривается как агрессивно настроенный и сознательно
действующий противник, как в матричной
игре. Поэтому выбирается стратегия, гарантирующая выигрыш не меньший, чем
«нижняя цена игры с природой». В соответствии с этим критерием из всех самых
неудачных результатов выбирается самый лучший. Это перестраховочная позиция
крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема,
когда, например, игрок не столько заинтересован в крупной удаче, сколько хочет
«застраховать» себя от неожиданных проигрышей.
Выбранное таким образом решение полностью исключает риск. Это означает, что ЛПР не может столкнуться с
худшим результатом, чем тот, на который он ориентируется. Это свойство
позволяет считать максиминный критерий Вальда одним из фундаментальных. Поэтому
в технических и экономических задачах он применяется чаще всего как
сознательно, так и неосознанно. Таким критерием часто пользуются и в обиходе.
Использование критерия Вальда подтверждается известными поговорками:
«Береженого Бог бережет», «Лучше синица в руках, чем журавль в небе», «Семь раз
отмерь, один отрежь». Максиминный критерий Вальда (критерий гарантированного
результата) обеспечивает максимизацию минимального выигрыша, или, что то же
самое, минимизацию максимальных потерь, которые могут произойти при выборе
одной из стратегий. Выбор такой
стратегии определяется отношением игрока к риску.
КАК ВЫБИРАЮТ ОПТИМАЛЬНУЮ
СТРАТЕГИЮ СОГЛАСНО МАКСИМИННОМУ КРИТЕРИЮ ВАЛЬДА?
Обозначим
показатель эффективности стратегии Аi по максиминному критерию Вальда
через Wi. Для показателя эффективности Wi имеем формулу:
Wi
= min
aij, 1 ≤j ≤ n; i=1, …, m. (1)
Таким образом, показатель
эффективности Wi
стратегии Аi по максиминному критерию Вальда есть минимальный выигрыш игрока A при применении им этой
стратегии.
Цена
игры по максиминному критерию Вальда (обозначим ее через W) находится по
формуле:
W
= max
Wi,
1≤i≤m. (2)
Оптимальной
среди чистых стратегий по критерию Вальда является стратегия Ak с максимальным показателем
эффективности: Wk
= W.
Сформулируем
правило выбора оптимальных решений в соответствии с максиминным критерием
Вальда.
Матрица
выигрышей дополняется ещё одним столбцом с элементами Wi , i = 1, …, m,
– показателями эффективности стратегий Ai . Действительное число Wi
равно минимальному выигрышу игрока A при применении им стратегии Ai
и определяется по формуле (1).
Среди всех чистых стратегий A1,
A2, …, Am , необходимо выбрать те стратегии
Ak , у которых показатель
эффективности Wk является максимальным (то есть Wk = W, где W определяется по формуле (2)).

Таким
образом, оптимальной среди чистых стратегий по максиминному критерию Вальда
считается та чистая стратегия, при
которой минимальный выигрыш является максимальным среди минимальных выигрышей
всех чистых стратегий. Выбор
оптимального решения, в общем случае, не является однозначным. Этому критерию
оптимальности может соответствовать несколько чистых стратегий. Выбранные таким образом варианты решений
полностью исключают риск. Это означает, что принимающий решение не может
столкнуться с худшим результатом, чем тот, на который он ориентируется. Какие
бы условия ни встретились, соответствующий результат не может оказаться ниже W. Оптимальная чистая стратегия по
критерию Вальда гарантирует при любых состояниях «ПРИРОДЫ» выигрыш, не меньший
«максимина» W.
Максиминный критерий Вальда является критерием крайнего пессимизма игрока A, поскольку игрок A,
принимая решение, действует по принципу наибольшей осторожности.
ПРИМЕР 2. (ВЫБОР ОПТИМАЛЬНОЙ
СТРАТЕГИИ ПО МАКСИМИННОМУ КРИТЕРИЮ ВАЛЬДА).
Допустим,
что предприятие готовится к переходу на новые виды продукции. При этом возможны
четыре решения A1,
A2,
A3,
A4.
Каждому из решений соответствует определенный вид выпуска продукции или их
сочетание. Результаты принятых решений
существенно зависят от экономической ситуации, которая неопределенна.
Экономическая ситуация зависит от структуры спроса на новую продукцию, которая
может быть трех типов Q1,
Q2,
Q3.
Выигрыши – действительные числа aij, которые характеризуют
относительную величину результата (например, доходы, прибыль и т.п.) для каждой
пары («решение», «ситуация») – (Ai,Qj). Пусть имеется следующая матрица выигрышей
(рисунок 4), которая не содержит доминируемых (в частности, дублируемых) строк.
Дополним эту матрицу столбцом Wi
показателей эффективности стратегий Ai. Значения Wi вычисляем по формуле (1). Затем
в столбце Wi
находим максимальный элемент W.
В
данном примере цена игры W,
определенная по формуле (2),
равна: W = max {0,3; 0,5;
0,3; 0,2} = 0,5.
|
Варианты ситуации Виды решений |
Q1 |
Q2 |
Q3 |
Wi = min aij j |
|
A1 |
0,3 |
0,8 |
0,4 |
0,3 |
|
A2 |
0,6 |
0,5 |
0,6 |
0,5 |
|
A3 |
0,4 |
0,3 |
0,8 |
0,3 |
|
A4 |
0,1 |
0,7 |
0,9 |
0,1 |
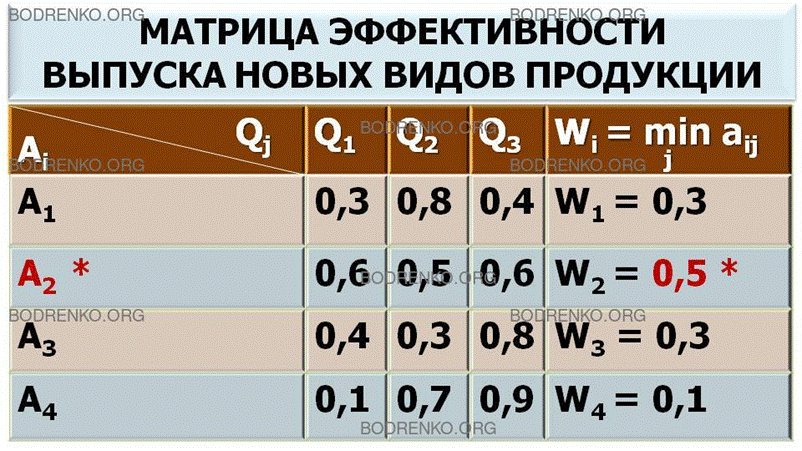
Рисунок 4. Матрица эффективности выпуска новых видов
продукции.
Таким
образом, по максиминному критерию Вальда (критерию гарантированного результата)
оптимальным решением является A2, так как показатель
эффективности W2 совпадает с «максимином» W (W2=W=0,5). Выбрав решение A2, мы независимо от вариантов
экономической ситуации получим выигрыш не менее 0,5. При любом другом решении в случае
неблагоприятной обстановки может быть получен результат (выигрыш), меньший
0,5.
Например,
при выборе решений A1 и A3 выигрыш будет колебаться от 0,3
до 0,8; а при выборе решения A4 – от 0,1 до 0,9. Отметим, что максиминный критерий Вальда
ориентирует ЛПР на крайне осторожную линию поведения. Например, этот критерий
не учитывает, что в случае выбора стратегии A2 (с гарантированным выигрышем
0,5) максимальный выигрыш не превышает 0,6. А при выборе стратегии A4 при гарантированном выигрыше 0,1
в благоприятной обстановке можно получить выигрыш, равный 0,9.
В КАКИХ СИТУАЦИЯХ
ПРИМЕНЯЕТСЯ МАКСИМИННЫЙ КРИТЕРИЙ ВАЛЬДА?
В
практических ситуациях излишний пессимизм этого критерия может оказаться очень
невыгодным. Пословица гласит: «Кто
боится собственной тени, тому нет места под солнцем». Применение максиминного критерия Вальда может
быть оправдано, если ситуация, в которой
он применяется, характеризуется следующими обстоятельствами.
- о
вероятности появления того или иного состояния Qj природы ничего не известно;
- с
появлением того или иного состояния Qj природы необходимо считаться;
-
реализуется лишь малое количество решений;
- не
допускается никакой риск, то есть ни при каком состоянии Qj не допускается получать выигрыш
меньший, чем W.
КРИТЕРИЙ МАКСИМАКСА
(КРИТЕРИЙ КРАЙНЕГО ОПТИМИЗМА).
При
использовании данного критерия игрок A (ЛПР) ориентируется на то, что
условия функционирования анализируемых систем будут для него благоприятными.
Вследствие этого оптимальным решением является та стратегия, которая приводит к
получению максимального значения критерия оптимальности в платежной
матрице. Критерий максимакса
максимизирует максимальные выигрыши для каждого состояния природы. Критерий
максимакса (крайнего оптимизма) противоположен максиминному критерию Вальда
(крайнего пессимизма). Игрок A,
пользуясь максимаксным критерием, предполагает, что природа Q будет находиться в
благоприятнейшем для него состоянии. Поэтому игрок A ведет себя легкомысленно, с
«шапкозакидательским» настроением, так как уверен в наибольшем выигрыше. Ситуации, требующие применения критерия
максимакса в экономике нередки. Пользуются им не только безоглядные оптимисты,
но и игроки, поставленные в безвыходное положение. Например, когда перед
игроком A
стоит дилемма: или получить наибольший выигрыш, или стать банкротом. В быту
подобные ситуации иллюстрируются
поговорками: «или пан, или пропал», «кто не рискует, тот не
выигрывает». Оптимальная чистая
стратегия по критерию максимакса гарантирует игроку A возможность выигрыша, равного «максимаксу».
КАК ВЫБИРАЮТ ОПТИМАЛЬНУЮ
СТРАТЕГИЮ СОГЛАСНО МАКСИМАКСНОМУ КРИТЕРИЮ?
Показатель
эффективности стратегии Ai
по максимаксному критерию обозначим через Mi и определим по формуле:
Mi = max aij, 1
≤j ≤ n; i=1, …, m. (3)
Таким образом, показатель
эффективности чистой стратегии Ai
по критерию максимакса равен максимальному выигрышу игрока A при выборе им этой стратегии.
Цена
игры M
по критерию максимакса определяется по формуле:
M
= max
Mi,
1≤i≤m. (4)
Оптимальная
стратегия по критерию максимакса определяется как стратегия Аk с максимальным
показателем эффективности: Mk
= M.

Сформулируем
правило выбора оптимальных решений в соответствии с критерием максимакса.
Матрица
выигрышей дополняется ещё одним столбцом с элементами Mi , i = 1, …, m,
– показателями эффективности стратегий
Ai . Действительное число Mi
равно максимальному выигрышу
игрока A
при применении им стратегии Ai и определяется по формуле (3). Среди всех чистых стратегий A1,
A2, …, Am , необходимо выбрать те стратегии
Ak , у которых показатель эффективности
Mk является максимальным (то есть Mk = M, где M определяется по формуле (4)).
КРИТЕРИЙ
ПРОИЗВЕДЕНИЙ В УСЛОВИЯХ ПОЛНОЙ
НЕОПРЕДЕЛЕННОСТИ.
С самого начала этот критерий
ориентирован на величины выигрышей, то есть
на положительные значения aij. Данный критерий применяется в
случае, когда все элементы матрицы выигрышей положительны: aij > 0, i= 1, …, m; j = 1, …, n.
КАК ВЫБИРАЮТ
ОПТИМАЛЬНУЮ СТРАТЕГИЮ ПО КРИТЕРИЮ ПРОИЗВЕДЕНИЙ?
Опишем критерий произведений
применительно к ситуациям полной неопределенности, то есть когда вероятности
состояний природы неизвестны.
Показатель эффективности стратегии Ai в соответствии с
критерием произведений в условиях полной неопределенности обозначим через Pi и определим по формуле:
Pi
= ∏ aij, 1 ≤j
≤ n;
i=1,
…, m.
(5)
Таким образом,
показатель эффективности Pi чистой стратегии Ai по критерию произведений (в условиях полной неопределенности)
равен произведению всех выигрышей игрока A при выборе им этой стратегии.
Цена игры P по критерию произведений определяется
по формуле:
P
= max
Pi,
1≤i≤m. (6)
Оптимальная стратегия Ak по критерию
произведений определяется как стратегия с максимальным показателем
эффективности Pk
= P.

Правило выбора оптимальной стратегии
по критерию произведений в условиях полной неопределенности формулируется так.
Матрица
выигрышей дополняется ещё одним столбцом с элементами Pi , i = 1, …, m,
– показателями эффективности
стратегий Ai . Действительное число Pi
равно произведению всех выигрышей
игрока A
при применении им стратегии Ai
и определяется по формуле (5). Среди всех чистых стратегий A1,
A2, …, Am , необходимо выбрать те стратегии
Ak , у которых показатель
эффективности Pk является максимальным (то есть Pk = P, где P определяется по формуле (6)).
КАКИМИ
ОБСТОЯТЕЛЬСТВАМИ ОБУСЛОВЛЕНО ПРИМЕНЕНИЕ КРИТЕРИЯ ПРОИЗВЕДЕНИЙ?
Применение критерия произведений (P-критерия)
в условиях полной неопределенности обусловлено
следующими обстоятельствами:
- вероятности появления состояний Qj
неизвестны;
- с появлением каждого из состояний Qj
по отдельности необходимо считаться;
- критерий применим и при малом числе
реализаций решения;
- некоторый риск допускается.
Если условие aij>0, i= 1,
…, m; j = 1, …, n;
нарушается, а P-критерий
приходится применять и в этом случае, то следует выполнить некоторый сдвиг (aij + b) каждого элемента матрицы
выигрышей aij
с некоторой константой b
> |min aij|.
Ясно, что результат применения P-критерия
существенно зависит от этого значения b. На практике в качестве значения b охотно
используют величину b = |min
aij|
+ 1. Если же никакая константа не может быть признана имеющей смысл, то к таким
проблемам Р-критерий не применим.
Выбор оптимального решения согласно
Р-критерию оказывается значительно менее
пессимистическим, чем, например, выбор в
соответствии с максиминным критерием Вальда.
В результате применения Р-критерия
происходит некоторое выравнивание между большими и малыми значениями выигрышей aij, и, устанавливая оптимальный вариант
решения с помощью Р-критерия, мы можем при фиксированных состояниях Qj получить
большую выгоду, чем при использовании критерия гарантированного результата, но
при этом должна учитываться возможность
появления и худших результатов.
Следует отметить, что при
использовании этого критерия ни число реализаций, ни информация о
распределении вероятностей не принимаются во внимание.
КРИТЕРИЙ
ПЕССИМИЗМА-ОПТИМИЗМА ГУРВИЦА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С ПОКАЗАТЕЛЕМ ОПТИМИЗМА λ.
Представляется
логичным, что при выборе оптимального решения вместо двух крайностей в оценке
ситуации придерживаться некоторой промежуточной позиции, учитывающей
возможность как наихудшего, так и наилучшего, благоприятного поведения природы Q. Такой компромиссный вариант и был предложен
Гурвицем. Стараясь занять уравновешенную
позицию, Гурвиц предложил критерий, оценочная функция которого находится где-то
между точками предельного оптимизма и крайнего пессимизма. Этот критерий при выборе решения рекомендует
руководствоваться некоторым средним результатом, характеризующим состояние
между крайним пессимизмом и безудержным оптимизмом.
Определим показатель эффективности Hi стратегии Ai по формуле:
Hi
= λ∙max aij + (1 – λ)∙min aij,
1 ≤j
≤ n; i=1, …, m, (7)
где число λ удовлетворяет условию: 0≤λ≤1.
В формуле (7) величина λ называется показателем оптимизма, соответственно (1 – λ) – это показатель пессимизма игрока A .
Цена игры H по критерию пессимизма-оптимизма Гурвица с показателем оптимизма λ определяется по формуле:
H
= max
Hi,
1≤i≤m. (8)
Согласно этому критерию оптимальная стратегия Ak выбирается в соответствии с максимальным показателем эффективности Hk = H.

Таким образом, согласно критерию пессимизма-оптимизма Гурвица для каждой стратегии Ai необходимо определить линейную комбинацию Hi минимального и максимального выигрышей при данной стратегии, и выбрать ту стратегию Ak, для которой величина Hk окажется максимальной. Чем ближе к единице показатель оптимизма λ, тем ближе к нулю показатель пессимизма (1 – λ), и тем больше оптимизма и меньше пессимизма. И наоборот. Таким образом, число λ выбирается в пределах от 0 до 1 в зависимости от склонности игрока A к оптимизму или пессимизму.
При показателе оптимизма λ = 1 критерий Гурвица превращается в критерий максимакса, а при λ=0 – совпадает c максиминным критерием Вальда. В случае, когда λ=0,5, то и (1–λ)=0,5. То есть показатели оптимизма и пессимизма одинаковы. Это означает, что игрок A при выборе стратегии ведет себя нейтрально. В прикладных задачах бывает трудно правильно выбрать значение показателя λ. Поэтому чаще всего весовой множитель λ=0,5 без возражений принимается в качестве некоторой «средней» точки зрения. На выбор значения показателя оптимизма λ оказывает влияние мера ответственности. Чем серьезнее последствия ошибочных решений, тем больше желание принимающего решение застраховаться, то есть показатель пессимизма (1 – λ) ближе к единице.
В КАКИХ СИТУАЦИЯХ
ОПРАВДАНО ПРИМЕНЕНИЕ КРИТЕРИЯ ГУРВИЦА?
Применение
критерия Гурвица оправдано, если ситуация, в которой он используется,
характеризуется следующими обстоятельствами.
- о вероятностях появления
состояний природы Qj ничего не известно;
- с появлением состояний природы
Qj необходимо считаться;
- реализуется лишь малое
количество решений;
- допускается некоторый риск.
ОБОБЩЕННЫЙ КРИТЕРИЙ
ПЕССИМИЗМА-ОПТИМИЗМА ГУРВИЦА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С КОЭФФИЦИЕНТАМИ λ1, λ2, …,
λn
(КРИТЕРИЙ ОБОБЩЕННОГО МАКСИМИНА ГУРВИЦА).
Для
применения этого критерия переставим в каждой строке Ai матрицы игры A выигрыши игрока 1 (ЛПР) в
неубывающем порядке. Обозначим элементы полученной матрицы через bij,
а саму матрицу - через B (рисунок 5).
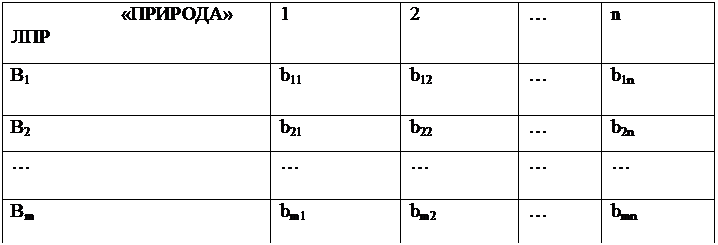
Рисунок 5. Матрица B.
Для
элементов матрицы B
(рисунок 5) имеем следующие неравенства:
bi1
≤ bi2
≤ … ≤ bin, i = 1,…, m. (9)
Матрица B получена из матрицы A перестановкой элементов каждой
ее строки в неубывающем порядке. В силу
неравенств (9) в первом столбце матрицы B расположены минимальные выигрыши
игрока A
при использовании стратегий Ai:
bi1=
min
aij, 1 ≤j ≤ n;
i=1,
…, m; в последнем столбце матрицы B – максимальные выигрыши при
использовании стратегий Ai:
bin=
max
aij, 1 ≤j ≤ n;
i=1,
…, m.

Другими
словами, в первом столбце матрицы B стоят показатели эффективности Wi
стратегий Ai
по максиминному критерию Вальда, а в n-м столбце – показатели
эффективности Mi
стратегий Ai
по критерию максимакса.
Рассмотрим
неотрицательные числа λ1≥0, λ2≥0, …, λn≥0, удовлетворяющие условию: ∑λj=1, j= 1, …, n.
Показателем
оптимизма игрока A называется число λo, определенное по формулам:
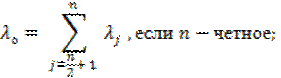
и
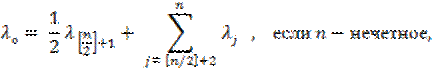
где [n/2]- целая часть числа n/2 , когда n - нечетное.

Соответственно,
показателем пессимизма игрока A называется число λp, определенное по формулам:
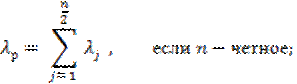
и
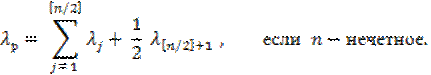
Очевидно,
что λo
+ λp
= 1.

КАК ВЫБИРАЮТ
ОПТИМАЛЬНУЮ СТРАТЕГИЮ ПО КРИТЕРИЮ ОБОБЩЕННОГО МАКСИМИНА
ГУРВИЦА?
Показатель
эффективности Gi
стратегии Аi по критерию обобщенного максимина Гурвица определяется по формуле:
Gi = ∑λj∙bij, 1 ≤j ≤ n;
i= 1, …, m. (10)
Цену
игры по критерию обобщенного максимина Гурвица определим по формуле:
G=
max
Gi,
1≤i≤m. (11)
Оптимальной
чистой стратегией является та стратегия Аk, для которой показатель
эффективности Gk является максимальным, то есть Gk=G.

Отметим,
что критерий обобщенного максимина Гурвица учитывает все выигрыши при каждой
стратегии, что необходимо для более полной картины эффективности стратегий.
КАКИЕ ЧАСТНЫЕ
СЛУЧАИ КРИТЕРИЯ ОБОБЩЕННОГО МАКСИМИНА ГУРВИЦА МОЖНО ОТМЕТИТЬ?
Отметим
следующие частные случаи критерия обобщенного максимина Гурвица.
СЛУЧАЙ 1.
Если λ1=1, λ2=…=λn=0, то критерий обобщенного
максимина Гурвица представляет собой максиминный критерий Вальда.
СЛУЧАЙ 2.
Если λ1= λ2=…=λn-1=0, λn=1, то из критерия обобщенного
максимина Гурвица получаем критерий максимакса.
СЛУЧАЙ 3.
Если λ1=(1-λ), λ2=…=λn-1=0, λn=λ, где 0≤λ≤1, то критерий обобщенного
максимина Гурвица является критерием пессимизма-оптимизма Гурвица относительно
выигрышей с показателем оптимизма λ.
КРИТЕРИЙ МИНИМАКСНОГО РИСКА
СЭВИДЖА.
На
практике, выбирая одно из возможных решений, часто останавливаются на том,
осуществление которого приведет к наименее тяжелым последствиям, если выбор
окажется ошибочным. Этот подход к выбору решения математически был
сформулирован американским статистиком Сэвиджем (Savage) и получил название «принципа Сэвиджа». Он особенно
удобен для экономических задач и часто применяется для выбора решений в играх
человека с природой. При выборе
возможной стратегии в игре с природой игрок A (игрок-ЛПР) должен исходить из матрицы выигрышей.
Однако, матрица выигрышей не всегда адекватно отражает имеющуюся ситуацию. По принципу Сэвиджа каждое решение
характеризуется величиной дополнительных потерь, которые возникают при
реализации этого решения, по сравнению с реализацией решения, «правильного» при
данном состоянии природы. Естественно считать, что «правильное» решение не
влечет за собой никаких дополнительных потерь, и их величина равна нулю. При
выборе решения, наилучшим образом соответствующего различным состояниям
природы, следует принимать во внимание только эти дополнительные потери,
которые по существу, будут являться следствием ошибок выбора. Для решения задачи строится так называемая
«матрица рисков», элементы которой показывают, какой убыток понесет игрок A (ЛПР) в результате выбора «неправильного» варианта
решения. В соответствии с критерием «минимального риска» на выбор стратегии
должны влиять не только выигрыши, составляющие матрицу решений. Должны учитываться показатели благоприятности
состояний природы для увеличения выигрыша и показатели удачности выбора игроком
A своей чистой стратегии Ai при состоянии природы Qj.
ЧТО ТАКОЕ ПОКАЗАТЕЛЬ
БЛАГОПРЯТНОСТИ СОСТОЯНИЯ Qj
ПРИРОДЫ Q?
ПОКАЗАТЕЛЕМ
БЛАГОПРИЯТНОСТИ СОСТОЯНИЯ
Qj
ПРИРОДЫ Q
называется максимальный выигрыш игрока А при этом состоянии, то есть
максимальный элемент j-го
столбца матрицы выигрышей:
βj
= max
aij,
1≤i
≤ m; j=1, …, n.
(12)

ЧТО ТАКОЕ РИСК
ИГРОКА?
Для
характеристики степени удачности выбора игроком А своей стратегии Ai при состоянии природы Qj, вводят понятие РИСКА.
РИСКОМ Rij ИГРОКА А ПРИ ВЫБОРЕ ИМ СТРАТЕГИИ
Ai
И ПРИ СОСТОЯНИИ ПРИРОДЫ Qj называют разность между показателем
благоприятности βj
и выигрышем aij:
Rij = βj – aij, i=1, …, m. (13)

Другими
словами, риск – это разность между выигрышем, который игрок А получил бы, если бы он точно знал, что
состоянием природы будет Qj, и выигрышем, который игрок А получит, не имея
этой информации и применяя свою стратегию Ai.
Таким образом, риск Rij
игрока А представляет собой упущенную возможность максимального выигрыша βj (то есть упущенную выгоду) при
данном состоянии природы Qj.
Эта упущенная возможность определяется невыигранной частью максимального
выигрыша. Следовательно, величину риска Rij можно интерпретировать как
своеобразную плату за отсутствие
информации о действительном состоянии
природы. Поскольку точная информация о состоянии природы Qj позволила бы игроку А выбрать ту
стратегию Ai, при которой его выигрыш был бы максимальным,
то есть βj.
ЧТО ТАКОЕ КОЛЕБАНИЕ
ВЫИГРЫШЕЙ ПРИ СОСТОЯНИИ ПРИРОДЫ Qj?
Введем
величину γj по формуле: γj = min aij, 1≤i ≤ m;
j=1,
…, n.
То есть
величина γj – это
минимальный выигрыш игрока А при
состоянии природы Qj.
Разность
(βj – γj) = (max aij – min aij), 1≤i ≤ m; j=1, …, n,
между
максимальным выигрышем βj
игрока А при состоянии природы Qj
и минимальным выигрышем γj
игрока А при этом состоянии называют КОЛЕБАНИЕМ ВЫИГРЫШЕЙ ПРИ СОСТОЯНИИ ПРИРОДЫ Qj.

Мы можем
установить границу изменения риска Rij:
0 ≤ Rij ≤ (βj - γj).
Для
данной матрицы выигрышей А размера «m x n» матрица рисков RA имеет тот же размер «m x n» (рисунок 6).
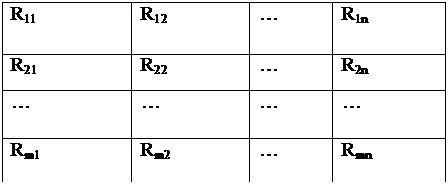

Рисунок 6. Матрица рисков RA.
ЧТО ПРОЯСНЯЕТ
МАТРИЦА РИСКОВ?
В игре с
природой возможны следующие ситуации.
1.
Возможны одинаковые выигрыши игрока 1 при одной и той же стратегии, но при
разных состояниях природы.
2.
Возможны одинаковые выигрыши игрока 1 при разных стратегиях, но при одном и том
же состоянии природы.
Матрица
рисков проясняет, насколько удачна стратегия Ai при разных состояниях
природы Qj и Ql
.
СЛУЧАЙ 1.
Пусть
стратегия Ai
дает одинаковые выигрыши aij
= ais при разных состояниях природы Qj и Qs, j≠s. При этом риски игрока А равны
соответственно Rij
и Ris
.
Если Rij < Ris , то выбор стратегии Ai по отношению к состоянию природы
Qj
более удачлив, чем по отношению к состоянию природы Qs.
То есть
МАТРИЦА РИСКОВ ПОКАЗЫВАЕТ НЕРАВНОЦЕННОСТЬ ОДИНАКОВЫХ ВЫИГРЫШЕЙ С ТОЧКИ ЗРЕНИЯ
РИСКОВ ПРИ ОДНОЙ И ТОЙ ЖЕ СТРАТЕГИИ, НО ПРИ РАЗНЫХ СОСТОЯНИЯХ ПРИРОДЫ.
СЛУЧАЙ 2.
Пусть
выигрыши игрока А одинаковы при разных стратегиях Ai, Ak , но при одном и том же
состоянии природы, то есть aij
= akj. В этом случае риски Rij и Rkj игрока 1 будут равны между
собой: Rij
= βj
– aij
= βj
– akj
= Rkj.
Таким
образом, С ТОЧКИ ЗРЕНИЯ РИСКОВ ОДИНАКОВЫЕ ВЫИГРЫШИ ИГРОКА А ПРИ РАЗНЫХ
СТРАТЕГИЯХ, НО ПРИ ОДНОМ И ТОМ ЖЕ СОСТОЯНИИ ПРИРОДЫ ВСЕГДА РАВНОЦЕННЫ.
КАК ВЫБРАТЬ ОПТИМАЛЬНУЮ
СТРАТЕГИЮ СОГЛАСНО КРИТЕРИЮ МИНИМАКСНОГО РИСКА СЭВИДЖА?
Критерий
минимаксного риска Сэвиджа аналогичен максиминному критерию Вальда. Показатель
эффективности Si
стратегии Ai
согласно критерию Сэвиджа определим по формуле:
Si = max Rij, 1≤j≤n; i=1, …, m. (14)
Таким
образом, показатель эффективности Si стратегии Ai по критерию Сэвиджа равен
максимальному риску игрока A
при выборе им этой стратегии.
Определим
значение S
для выбора оптимальной стратегии по формуле:
S=
min
Si,
1≤i≤m. (15)
В соответствии
с критерием Сэвиджа оптимальной является та стратегия Ak, которая имеет минимальный
показатель эффективности Sk
= S.

ПРИМЕР 2. (ВЫБОР
ОПТИМАЛЬНОЙ СТРАТЕГИИ ПО КРИТЕРИЮ МИНИМАКСНОГО РИСКА СЭВИДЖА).
Допустим,
компания производит продукцию определенного ассортимента и осуществляет ее сбыт
по четырем каналам:
-
ежемесячный объем продукции с устойчивым сбытом на ряд лет в среднем составляет
49000 у.е.;
-
ежемесячный объем продукции с устойчивым сбытом на один год в среднем
составляет 50000 у.е.;
-
ежемесячный объем продукции, обеспеченный разовой закупкой, составляет 51000
у.е.;
-
ежемесячный объем продукции, покупатель на которую заранее не определен,
составляет 40000 у.е.
Компания
может осуществлять производство продукции по трем проектам А1, А2, А3 в
объемах P1 = 98000 у.е., P2 = 150000 у.е., P3 = 198000 у.е., соответственно.
Требуется
выбрать оптимальную стратегию производства продукции.
Контролируемым
параметром является объем производства, ему соответствуют три стратегии A1, A2, A3. Объем производства при
стратегии Ai выражается числовым значением Рi.
Неконтролируемым
параметром является колебание спроса. Ему соответствуют четыре варианта
экономической обстановки: Q1
– низкая зависимость колебания спроса от изменения рыночной конъюнктуры, Q2 – средняя зависимость, Q3 – высокая зависимость, Q4 – абсолютная зависимость.
Размер
прибыли компании, соответствующий состоянию Qj,
выражается числовым значением Dj.
В зависимости от изменения рыночной конъюнктуры в связи с имеющимися возможностями
реализации рассчитаны варианты среднегодовой прибыли, которые представлены в
виде матрицы платежеспособного спроса (рисунок 7). При расчете среднегодовой
прибыли учитываются потери, связанные, например, с хранением нереализованной
продукции и другие. В данном случае
при построении платежной матрицы первостепенную роль имеют пропорции исходных и
результативных показателей. Поскольку вызванные инфляционными процессами
изменения цен, оказывая влияние на абсолютные величины, не изменяют их пропорциональных
соотношений. Это позволяет использовать данную методику в условиях инфляции без дополнительных
расчетов.
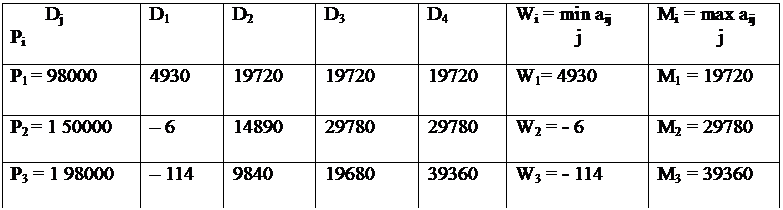
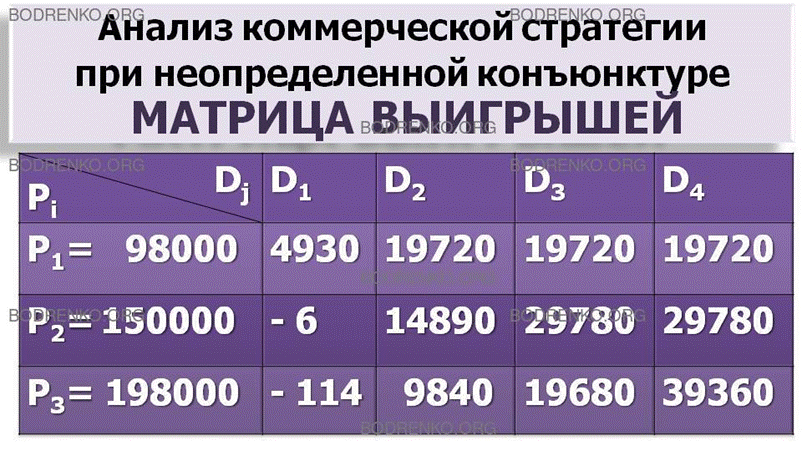
Рисунок 7. Анализ коммерческой стратегии при неопределенной конъюнктуре.
По матрице выигрышей (рисунок 7) построим матрицу рисков (рисунок 8).
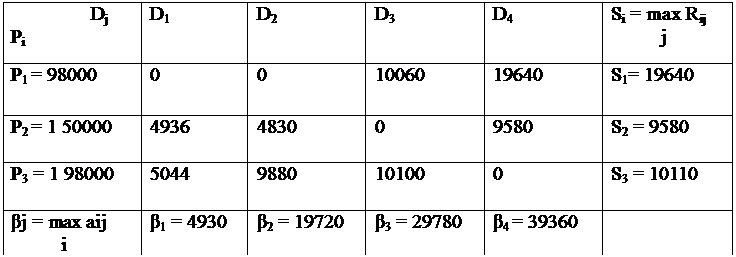
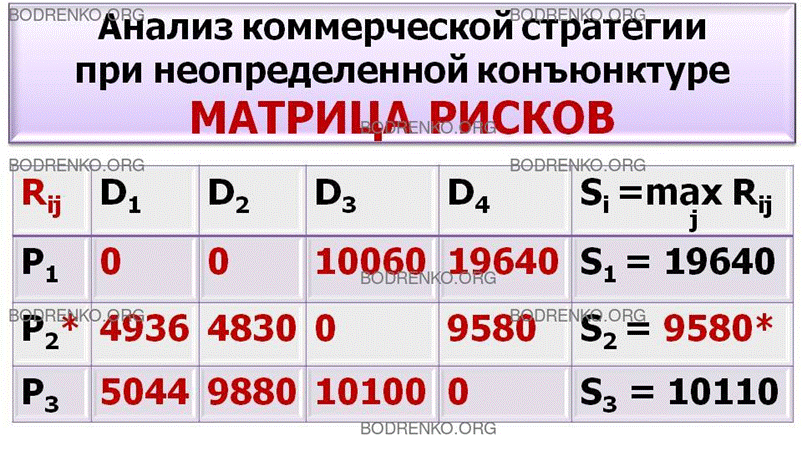
Рисунок 8. Матрица рисков {Rij}.
По критерию
минимаксного риска Сэвиджа найдем
оптимальную стратегию.
При стратегии A2
величина риска S2 = 9580 принимает минимальное
значение в самой неблагоприятной
экономической ситуации. Сущность этого критерия – стремление избежать
большого риска при выборе решения. В соответствии с этим критерием следует
производить продукцию в объеме P2 = 150000 у.е.
Таким образом, критерий Сэвиджа минимизирует
возможные потери. Основным исходным допущением этого критерия является
предположение, что на выбор вариантов
ситуации влияют действия разумных противников (природы), интересы которых прямо
противоположны интересам ЛПР. Поэтому
если у противников (конкурентов) имеются возможности извлечь какие-либо
преимущества, то они это обязательно сделают. Это обстоятельство заставляет ЛПР
обеспечить минимизацию потерь вследствие этих действий.
КРИТЕРИЙ ПЕССИМИЗМА-ОПТИМИЗМА ГУРВИЦА ОТНОСИТЕЛЬНО
РИСКОВ.
Согласно
этому критерию для каждой стратегии Ai необходимо определить показатель
эффективности HRi как линейную комбинацию
минимального и максимального рисков при данной стратегии:
HRi = p∙max Rij + (1 – p)∙min Rij, 1 ≤j ≤ n;
i=1, …, m, (16)
где
число p удовлетворяет условию: 0≤ p≤1.![]()
Определим
значение HR
для выбора оптимальной стратегии по формуле:
HR= min HRi, 1≤i≤m. (17)
В
соответствии с критерием пессимизма-оптимизма Гурвица относительно рисков в
качестве оптимальной стратегии выбирают ту стратегию Ak, для которой показатель
эффективности HRk
является минимальным: HRk = HR.

В
частности, при p=1 выбор оптимальной стратегии
осуществляется по критерию минимаксного риска Сэвиджа.
ПРИМЕР 3. (ВЫБОР
ОПТИМАЛЬНОЙ СТРАТЕГИИ В ИГРЕ «С ПРИРОДОЙ» В УСЛОВИЯХ ПОЛНОЙ НЕОПРЕДЕЛЕННОСТИ).
Применим
рассмотренные критерии для выбора оптимального решения на следующем
примере.
Допустим,
инвестор принимает решение о строительстве жилья определенного типа в некотором
месте. Инвестор действует в условиях неопределенности (информационной
непрозрачности) на рынке жилья. Чтобы сформировать представление о ситуации на
рынке жилья на момент завершения строительства ему необходимо учесть цены на
недвижимость, конкуренцию на рынке жилья, соотношение предложения и спроса,
курсы валют и многое другое. Статистические данные свидетельствуют о том, что
одной из главных составляющих стоимости жилья является место его расположения.
Рассмотрим
математическую модель данной ситуации. Мы имеем игру с природой, где игрок A – инвестор, природа Q– совокупность возможных ситуаций
на рынке жилья на момент завершения строительства, из которых можно
сформировать, например, пять состояний Q1, Q2, Q3, Q4, Q5 природы. Предположим, что игрок
A
располагает четырьмя (чистыми) стратегиями А1, А2, А3, А4, представляющими
собой выбор определенного места для постройки жилья. Множество этих мест
ограничено градостроительными решениями, стоимостью земли и т.д.
Инвестиционная
привлекательность проекта определяется как процент прироста дохода по отношению
к сумме капитальных вложений, оценка которых известна при каждой стратегии и
каждом состоянии природы. Эти данные представлены в следующей матрице выигрышей
игрока A
(рисунок 9).
|
Состояния «ПРИРОДЫ» Стратегии ЛПР |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
|
A1 |
1 |
6 |
2 |
14 |
5 |
|
A2 |
3 |
5 |
10 |
2 |
4 |
|
A3 |
5 |
3 |
8 |
9 |
4 |
|
A4 |
2 |
7 |
6 |
8 |
4 |

Рисунок 9. Выбор проекта
инвестиций в игре «с природой».
Матрица
решений (рисунок 9) не содержит доминируемых (дублируемых) строк и все ее
элементы положительны.
Инвестору
предстоит выбрать участок земли так, чтобы наиболее эффективно использовать
капиталовложения.
Для
данной матрицы решений (рисунок 9) вычислим показатели эффективности стратегий
относительно выигрышей по следующим четырем критериям:
1) по
максиминному критерию Вальда;
2) по
критерию максимакса;
3) по
критерию произведений (в условиях полной неопределенности);
4) по
критерию пессимизма-оптимизма Гурвица относительно выигрышей (с показателем
оптимизма λ =0,4);
5) по
обобщенному критерию пессимизма-оптимизма Гурвица (с коэффициентами λ1=0,35,
λ2=0,2, λ3=0,2, λ4=0,15, λ5=0,1).
А также,
вычислим показатели эффективности стратегий относительно рисков по критерию
минимаксного риска Сэвиджа.
Дополним
матрицу выигрышей столбцами с показателями эффективности Wi и Mi стратегий Ai по критериям Вальда, максимакса
и произведений, соответственно. Применяя
формулы (1), (3) и (5), мы получим:
|
Состояния «ПРИРОДЫ» Стратегии ЛПР |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
Wi |
Mi |
Pi |
|
A1 |
1 |
6 |
2 |
14 |
5 |
1 |
14 |
840 |
|
A2 |
3 |
5 |
10 |
2 |
4 |
2 |
10 |
1200 |
|
A3 |
5 |
3 |
6 |
9 |
4 |
3 |
9 |
3240 |
|
A4 |
2 |
7 |
6 |
8 |
4 |
2 |
8 |
2688 |
1.
В соответствии с формулой (9) построим матрицу
B (рисунок 10) для критерия обобщенного
максимина Гурвица. Мы имеем:
|
Стратегии ЛПР |
1 |
2 |
3 |
4 |
5 |
|
A1 |
1 |
2 |
5 |
6 |
14 |
|
A2 |
2 |
3 |
4 |
5 |
10 |
|
A3 |
3 |
4 |
5 |
6 |
9 |
|
A4 |
2 |
4 |
6 |
7 |
8 |
Рисунок 10. Матрица B.
Используя
формулы (10), вычислим показатели эффективности Gi стратегий Ai по критерию обобщенного максимина Гурвица. Мы
имеем: G1=4,05; G2 =3,85; G3 =4,65; G4 =4,55.
![]()
![]()
![]()
![]()
В обобщенном критерии Гурвица показатель пессимизма λp=0,65, показатель оптимизма λo=1 – λp = 0,35.
Таким образом, в применяемых критериях, учитывающих индивидуальные проявления игрока A к пессимизму и оптимизму (критерий пессимизма-оптимизма Гурвица и критерий обобщенного максимина Гурвица), игрок A более склонен к пессимистической оценке ситуации, чем к оптимистической.
Для применения
критерия Сэвиджа по данной матрице
выигрышей (рисунок 9) найдем матрицу рисков (рисунок 11). Вычисляя показатели благоприятности состояний
природы Qj
по формулам (12), и применяя затем формулы (13), получим следующую матрицу
рисков.
|
Состояния «ПРИРОДЫ» Стратегии ЛПР |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
Si |
|
A1 |
5-1 |
7-6 |
10-2 |
14-14 |
5-5 |
8 |
|
A2 |
5-3 |
7-5 |
10-10 |
14-2 |
5-4 |
12 |
|
A3 * |
5-5 |
7-3 |
10-6 |
14-9 |
5-4 |
5 |
|
A4 |
5-2 |
7-7 |
10-6 |
14-8 |
5-4 |
6 |
|
βj |
5 |
7 |
10 |
14 |
5 |
|

Рисунок 11. Матрица рисков и показатели эффективности
стратегий.
Затем по
формулам (14) находим показатели эффективности Si стратегий Ai.
Значение S
вычисляем по формуле (15). В данной
задаче S
= 5. Согласно критерию Сэвиджа оптимальная стратегия Ak – это стратегия, для
которой Sk = S.
Этому показателю эффективности по критерию Сэвиджа соответствует
стратегия A3.
Результаты
подсчета показателей эффективности и оптимальные стратегии представлены в
следующей таблице (рисунок 12).
|
Критерии: Стратегии |
Вальда |
максимакса |
произведений |
Гурвица ( λ = 0,4) |
Обобщенный критерий Гурвица: λ1 = 0,35;
λ2 = 0,2; λ3 = 0,2; λ4 = 0,15; λ5 = 0,1. |
Сэвиджа |
|
A1 |
1 |
14
* |
840 |
6,2
* |
4,05 |
8 |
|
A2 |
2 |
10 |
1200 |
5,2 |
3,85 |
12 |
|
A3 |
3
* |
9 |
3240 * |
5,4 |
4,65
* |
5 * |
|
A4 |
2 |
8 |
2688 |
4,4 |
4,55 |
6 |
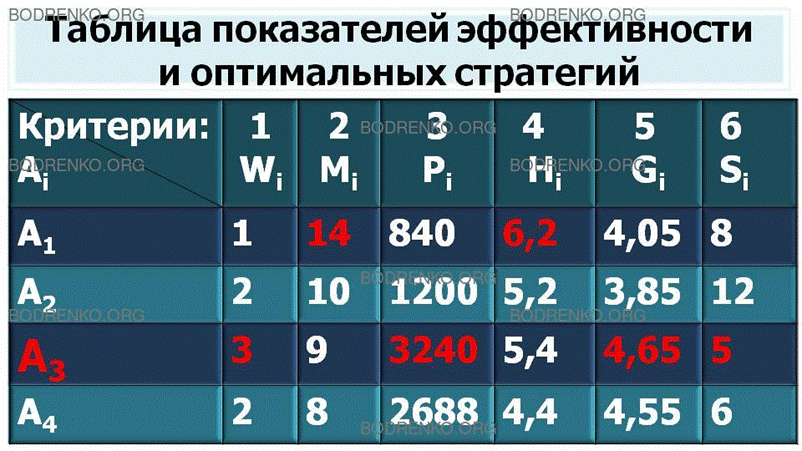
Рисунок 12. Таблица показателей
эффективности и оптимальных стратегий.
В
результате применения шести критериев мы видим, что в качестве оптимальной
стратегии четыре раза выступает стратегия A3, два раза – стратегия A1. Поэтому, если у инвестора
(игрока A)
нет никаких обоснованных серьезных возражений, то в качестве оптимальной
стратегии можно рассматривать стратегию А3.
РАЗДЕЛ 3. КРИТЕРИИ ВЫБОРА ОПТИМАЛЬНЫХ РЕШЕНИЙ В
УСЛОВИЯХ РИСКА.
Рассмотрим «игру с природой» в
условиях риска. Пусть у игрока A
имеется m возможных стратегий A1, А2, ..., Am,
и можно сделать n предположений о состояниях природы (среды) Q1, Q2,
..., Qn, с известными вероятностями их
появления p1, p2, …, pn, соответственно.
Пусть известен выигрыш aij, i = 1, …, m, j = 1, …, n, который получает
игрок A
при выборе стратегии Ai для каждого состояния природы Qj. Рассмотрим вероятностный вектор p = (p1, p2, …, pn), где элементы pj >
0 - это вероятности соответствующих
состояний Qj
природы Q.
Тогда можно
составить платежную матрицу игры «с природой»
следующего вида (рисунок
13).
|
Стратегии игрока A |
Состояния природы Q |
|||||
|
p1 |
… |
pj |
… |
pn |
||
|
Q1 |
… |
Qj |
… |
Qn |
||
|
A1 |
a11 |
… |
a1j |
… |
a1n |
|
|
… |
… |
… |
… |
… |
… |
|
|
Ai |
ai1 |
… |
aij |
… |
ain |
|
|
… |
… |
… |
… |
… |
… |
|
|
Am |
am1 |
… |
amj |
… |
amn |
|
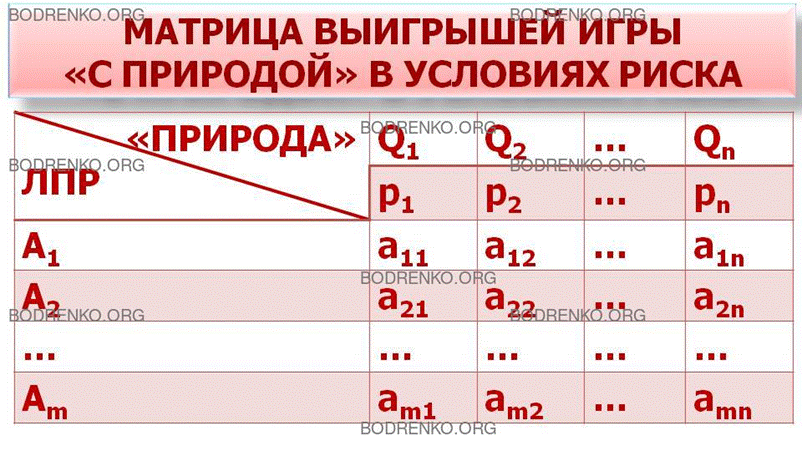
Рисунок
13. Платёжная матрица игры «с природой» с вероятностным вектором состояний
«природы».
Выбирая
стратегию Ai, игрок A знает, что получит один из выигрышей ai1, …, ain с
вероятностями p1, …, pn, соответственно. Следовательно, исходом для игрока A при выборе им
стратегии Ai,
является случайная величина ξi:
![]()
Итак,
сравнение двух стратегий Ai и Ak сводится к сравнению соответствующих им
случайных величин ξi и ξk.
КАКОВЫ КРИТЕРИИ
ВЫБОРА ОПТИМАЛЬНЫХ РЕШЕНИЙ В УСЛОВИЯХ РИСКА?
Мы изучим следующие критерии принятия решений в игре с
«природой» в условиях риска (стохастической неопределенности).
1. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО
ВЫИГРЫШЕЙ (КРИТЕРИЙ МАКСИМУМА ОЖИДАЕМОГО СРЕДНЕГО ВЫИГРЫША).
2. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО
РИСКОВ (КРИТЕРИЙ МИНИМУМА ОЖИДАЕМОГО СРЕДНЕГО РИСКА).
3. КРИТЕРИЙ ЛАПЛАСА ОТНОСИТЕЛЬНО
ВЫИГРЫШЕЙ (КРИТЕРИЙ «НЕДОСТАТОЧНОГО
ОСНОВАНИЯ» ЛАПЛАСА).
4. КРИТЕРИЙ ЛАПЛАСА ОТНОСИТЕЛЬНО
РИСКОВ.
5. КРИТЕРИЙ ХОДЖА-ЛЕМАНА.
6. КРИТЕРИЙ ГЕРМЕЙЕРА.
7. КРИТЕРИЙ ПРОИЗВЕДЕНИЙ С УЧЕТОМ
ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ «ПРИРОДЫ».
8. МАКСИМАКСНЫЙ КРИТЕРИЙ С УЧЕТОМ
ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ «ПРИРОДЫ».
9.
КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С УЧЕТОМ ОТНОСИТЕЛЬНЫХ ЗНАЧЕНИЙ
ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ ПРИРОДЫ.
10.
КРИТЕРИЙ МИНИМИЗАЦИИ СРЕДНЕГО КВАДРАТИЧНОГО ОТКЛОНЕНИЯ (ВАРИАЦИИ).
1. КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ (КРИТЕРИЙ
МАКСИМУМА ОЖИДАЕМОГО СРЕДНЕГО ВЫИГРЫША).
В
случае стохастической неопределенности, когда неуправляемым факторам
(состояниям природы) поставлены в соответствие вероятности, заданные экспертно,
или вычисленные, решение часто принимается на основе критерия максимума ожидаемого
среднего выигрыша (критерий Байеса относительно выигрышей) или минимума
ожидаемого среднего риска (критерий Байеса относительно рисков).
Обозначим
показатель эффективности стратегии Аi по критерии Байеса относительно
выигрышей через Bi.
Для показателя
эффективности Bi
имеем формулу:
Bi = ∑ pj∙aij, 1≤j≤n; i=1, …, m. (18)
Таким образом, показатель
эффективности Bi
стратегии Аi по критерию Байеса равен среднему значению (математическому ожиданию)
выигрыша с учетом вероятностей pj
всех возможных состояний Qj,
j
= 1, …, n, «ПРИРОДЫ» Q.
Цена
игры по критерию Байеса (обозначим ее
через B)
находится по формуле:
B
= max
Bi,
1≤i≤m. (19)
Оптимальной
среди чистых стратегий по критерию Байеса является стратегия Ak с максимальным показателем эффективности:
Bk=B.

КАК ВЫБРАТЬ
ОПТИМАЛЬНУЮ СТРАТЕГИЮ СОГЛАСНО КРИТЕРИЮ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ?
Сформулируем
правило выбора оптимальных решений в соответствии с критерием Байеса
относительно выигрышей.
Матрица
выигрышей дополняется ещё одним столбцом с элементами Bi , i = 1, …, m,
– показателями эффективности стратегий Ai . Действительное число Bi
равно среднему значению (математическому ожиданию) выигрыша игрока A при применении им стратегии Ai
и определяется по формуле (18).
Среди всех чистых стратегий A1,
A2, …, Am , необходимо выбрать те стратегии
Ak , у которых показатель
эффективности Bk является максимальным (то есть Bk = B, где B определяется по формуле (19)).
В КАКИХ СИТУАЦИЯХ
ОПРАВДАНО ПРИМЕНЕНИЕ КРИТЕРИЯ БАЙЕСА?
Решение, выбранное согласно
критерию Байеса, является оптимальным не в каждом отдельном случае, а «в
среднем». При этом предполагается, что
ситуация, в которой принимается решение,
характеризуется следующими
обстоятельствами:
- вероятности появления состояний
природы Qj известны и не зависят от
времени;
-
решение реализуется (теоретически) бесконечно много раз;
- для малого числа реализаций
решения допускается некоторый риск.
Исходная позиция применяющего
критерий Байеса предполагает более
высокий уровень информированности о вероятностях состояний Qj
«ПРИРОДЫ» и достаточно длинные реализации. При достаточно большом количестве
реализаций среднее значение постепенно стабилизируется. Поэтому при полной
(бесконечной) реализации какой-либо риск практически исключен.
ПРИМЕР 4. (ВЫБОР ОПТИМАЛЬНОГО ВАРИАНТА КАПИТАЛОВЛОЖЕНИЙ ПРИ
СТРОИТЕЛЬСТВЕ ЭЛЕКТРОСТАНЦИЙ).
Рассмотрим применение критерия Байеса относительно
выигрышей на следующем примере. Необходимо
построить в регионе электростанцию большой мощности. В данном регионе имеются
следующие возможности:
-
A1 - построение большого водохранилища и гидроэлектростанции;
-
A2 - сооружение тепловой электростанции на основном (газовом) топливе и
резервном (мазуте);
-
A3 - сооружение атомной электростанции.
Игрок A имеет три возможных решения A1, A2, A3.
Экономическая эффективность каждого варианта рассчитана проектным институтом,
который учитывал затраты на строительство и эксплуатационные расходы.
- На эксплуатационные расходы гидроэлектростанции
влияют климатические условия, например, такие, как погодные условия,
определяющие уровень воды в водохранилищах.
- Большое число случайных факторов воздействует на
экономическую эффективность тепловой станции: цены на мазут и газ, срывы
поставок мазута из-за неритмичности работы транспорта в зимнее время, особенно
во время снегопадов и продолжительных морозов.
- Экономическая эффективность атомной электростанции
будет зависеть от больших затрат на строительство и устойчивости агрегатов и
системы управления во время эксплуатации.
Таким образом, погодные условия будут в основном
сказываться на расходах по эксплуатации гидроэлектростанции и тепловой
электростанции. Следовательно, на эффективность тепловой электростанции будут
влиять как погодные условия, так и цены на газ и мазут.
Случайные факторы, от которых зависит экономическая
эффективность вариантов капиталовложений, объединим в четыре возможных
состояния природы - Q
= (Q1, Q2, Q3, Q4) с учетом окупаемости:
Q1 - цены на газ и мазут низкие и
климатические условия благоприятные;
Q2 - цены на газ и мазут высокие и
климатические условия благоприятные;
Q3 - цены на газ и мазут низкие и
климатические условия неблагоприятные;
Q4 – цены на газ и мазут высокие и
климатические условия неблагоприятные.
Полученные расчеты эффективности капиталовложений
при строительстве электростанций приведены в следующей матрице эффективности
(рисунок 14).
|
Состояния «ПРИРОДЫ» Стратегии игрока A |
Q1 |
Q2 |
Q3 |
Q4 |
|
A1 - ГИДРОЭЛЕКТРОСТАНЦИЯ |
75 |
75 |
35 |
35 |
|
A2 – ТЕПЛОВАЯ
ЭЛЕКТРОСТАНЦИЯ |
60 |
35 |
50 |
30 |
|
A3 – АТОМНАЯ
ЭЛЕКТРОСТАНЦИЯ |
45 |
45 |
45 |
45 |

Рисунок 14. Матрица
эффективности.
С помощью имеющихся временных рядов можно получить
апостериорную информацию, поскольку о влиянии на цены за газ, мазут таких
состоянии, как наводнения, засухи, морозы, сильные снегопады и т.п., существует
статистическая информация.
По данным многолетней статистики цен и состояний
получены оценки апостериорного распределения состояний Qj природы Q.
Данные непосредственного наблюдения состояний
природы позволили получить апостериорное распределение состояний природы:
p1
= P(Q1) = 0,15; p2 = P(Q2) = 0,30; p3= Р(Q3) = 0,20; p4 = P(Q4) = 0,35.
С учетом вероятностей состояний «ПРИРОДЫ» вычислим
показатели эффективности стратегий A1, A2, A3 согласно критерию Байеса.
Получим следующие значения математических ожиданий
выигрыша для каждой стратегии игрока A.
B1 = p1∙
a11+ p2∙ a12 + p3 ∙a13 + p4 ∙ a14 = 0,15 ∙ 75 + 0,30 ∙ 75 + 0,20 ∙ 35 + 0,35 ∙
35 = 53;
B2 = p1∙
a21+ p2∙ a22 + p3 ∙a23 + p4 ∙ a24 = 0,15 ∙ 60 + 0,30 ∙ 35 + 0,20 ∙ 50 + 0,35 ∙
30 = 40;
B3 = p1∙
a31+ p2∙ a32 + p3 ∙a33 + p4 ∙ a34 = 0,15 ∙ 45 + 0,30 ∙ 45 + 0,20 ∙ 45 + 0,35 ∙
45 = 45;

Цена игры по критерию Байеса равна
B
= max
{53, 40, 45} = 53.
Вывод. В соответствии с критерием Байеса
относительно выигрышей оптимальным решением будет инвестирование средств в
проект A1 - в строительство гидроэлектростанции.
КРИТЕРИЙ БАЙЕСА ОТНОСИТЕЛЬНО РИСКОВ (КРИТЕРИЙ МИНИМУМА
ОЖИДАЕМОГО СРЕДНЕГО РИСКА).
Для
применения критерий Байеса относительно рисков по исходной платежной матрице строится
матрица рисков R = {Rij}(mxn).
Показателем эффективности BRi
стратегии Ai по критерию Байеса относительно рисков называется математическое
ожидание рисков, расположенных в i-й строке матрицы рисков {Rij}:
BRi = ∑ pj∙Rij, 1≤j≤n; i=1, …, m. (20)
Оптимальной будет стратегия с
минимальным значением среднего риска:
B
= min
BRi,
1≤i≤m. (21)
Чистая стратегия Ak игрока A будет оптимальной стратегией, если BRk
= BR.

КАК ВЫБРАТЬ
ОПТИМАЛЬНУЮ СТРАТЕГИЮ СОГЛАСНО КРИТЕРИЮ БАЙЕСА ОТНОСИТЕЛЬНО РИСКОВ?
Сформулируем
правило выбора оптимальных решений в соответствии с критерием Байеса
относительно рисков (критерий минимума ожидаемого среднего риска). Матрица
рисков дополняется ещё одним столбцом с элементами BRi , i = 1, …, m, –
показателями эффективности стратегий Ai . Действительное число BRi равно среднему
значению (математическому ожиданию) риска
игрока A при применении им стратегии Ai и определяется
по формуле (20). Среди всех чистых
стратегий A1, A2, …, Am ,
необходимо выбрать те стратегии Ak , у
которых показатель эффективности BRk является минимальным (то есть BRk =
BR, где BR определяется
по формуле (21)).
При этом
справедливо утверждение о том, что критерии Байеса относительно выигрышей и
относительно рисков эквивалентны, то есть по обоим критериям оптимальной будет
одна та же стратегия.
ПРИМЕР
5. (ВЫБОР ОПТИМАЛЬНОЙ СТРАТЕГИИ ПО КРИТЕРИЮ БАЙЕСА
ОТНОСИТЕЛЬНО РИСКОВ).
Рассмотрим
применение критерия минимума ожидаемого среднего риска на следующем примере.
На
промышленном предприятии готовятся к переходу на выпуск новых видов продукции
A1, A2 , A3 , A4 . Результаты принятых решений существенно зависят от степени
обеспеченности производства материальными ресурсами Q1 , Q2 , Q3 .
Каждому
сочетанию (Ai, Qj) решений A i , i = 1,2, 3, 4, и состояний среды Qj , j = 1,2,3,
соответствует определенный выигрыш aij –
эффективность выпуска новых видов продукции. Всевозможные выигрыши
представлены в матрице эффективности (рисунок 15):
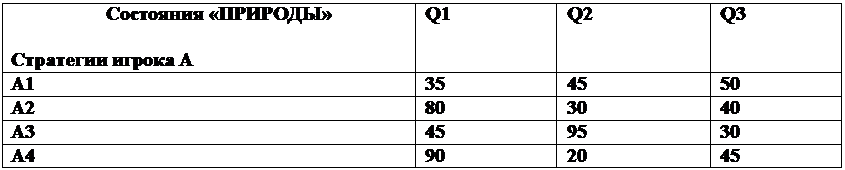

Рисунок 15. Матрица эффективности выпуска новых
видов продукции.
Найдем оптимальную стратегию игрока
A
в предположении, что известны вероятности состояний «ПРИРОДЫ»: p1= 0,15; p2 = 0,35,
p3
= 0,5.
Построим матрицу рисков для данной
игры «с природой» (рисунок 16). Мы имеем
|
Состояния «ПРИРОДЫ» Стратегии игрока A |
Q1 |
Q2 |
Q3 |
|
A1 |
R11 = 55 |
R12 = 50 |
R13 = 0 |
|
A2 |
R21= 10 |
R22 = 65 |
R23 = 10 |
|
A3 |
R31= 45 |
R32 = 0 |
R33= 20 |
|
A4 |
R41= 0 |
R42 = 75 |
R43 = 5 |
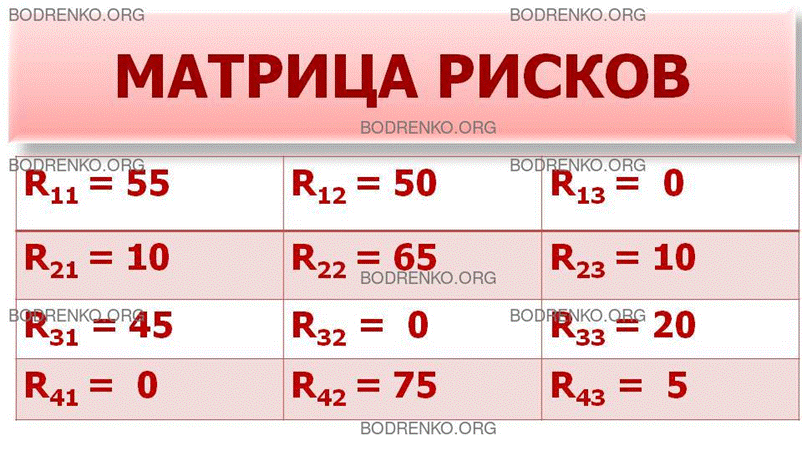
Рисунок
16.
Матрица рисков.
Находим ожидаемые средние риски
игрока A.
BR1 = p1∙ R11+ p2∙ R12 + p3 ∙R13 = 0,15 ∙ 55 + 0,35 ∙ 50 + 0,50
∙ 0 = 25,75;
BR2 = p1∙ R21+ p2∙ R22 + p3 ∙R23 = 0,15 ∙ 10 + 0,35 ∙ 65 + 0,50
∙ 10 = 29,25;
BR3 = p1∙ R31+ p2∙ R32 + p3 ∙R33 = 0,15 ∙ 45 + 0,35 ∙ 0 + 0,50
∙ 20 = 16,75;
BR4 = p1∙ R41+ p2∙ R42 + p3 ∙R43 = 0,15 ∙ 0 + 0,35 ∙ 75 + 0,50
∙ 5 = 28,75;

BR
= min
{25,75; 29,25; 16,75; 28,75} = 16,75.
ВЫВОД. В соответствии с критерием Байеса
относительно рисков оптимальным решением будет стратегия A3.
ЗАМЕЧАНИЕ. По критерию
Байеса относительно выигрышей показатели эффективности Bi стратегий Ai имеют
следующие значения: B1 = 46; B2= 42,5; B3 = 55; B4 = 43.
Следовательно,
цена игры B = max {46; 42,5; 55; 43} = 55. Значит, оптимальной
является стратегия A3.
КРИТЕРИЙ ЛАПЛАСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ (КРИТЕРИЙ
«НЕДОСТАТОЧНОГО ОСНОВАНИЯ»).
В предыдущих двух критериях Байеса
известные вероятности состояний природы могли быть получены, например, на
основании статистических исследований. Однако часто складывается такая
ситуация, при которой мы лишены возможности определить эти вероятности. Но,
желая принять решение в условиях риска, мы вынуждены оценивать эти вероятности
состояний природы субъективно.
Существуют различные методы численной субъективной оценки степени
правдоподобности состояний природы. Один из таких способов заключается в том,
что мы считаем состояния природы Qj равновероятными: p1 = p2 = ... =
pn = 1/n.
То есть мы не можем отдать предпочтение ни одному из состояний Qj
«ПРИРОДЫ» Q.
Этот принцип называют еще принципом «недостаточного основания» Лапласа.
Таким образом, показатель
эффективности Li
стратегии Ai
будет равен:
Li =
(1/n)∙∑ aij, 1≤j≤n; i=1, …, m. (22)
Цена игры по критерию Лапласа
равна:
L
= max Li;
1≤i≤m. (23)
Оптимальная стратегия Ak
определяется по формуле: Lk
= L.

ПРИМЕР 6. (ВЫБОР ОПТИМАЛЬНОЙ СТРАТЕГИИ ПО КРИТЕРИЮ
ЛАПЛАСА).
Найдем оптимальную стратегию в условиях по критерию
Лапласа для игры «с природой», заданной матрицей эффективности (рисунок 15).
Решение. Вычислим средние выигрыши:
L1
= 1/3(35+45+50) = 130/3;
L2
= 1/3 (80+30+40) = 150/3;
L3
= 1/3 (45+95+30) = 170/3;
L4
= 1/3 (90+20+45) = 155/3.

Следовательно, оптимальной по
критерию Лапласа является стратегия A3, так как показатель эффективности
L3
= max Li.
КРИТЕРИЙ ЛАПЛАСА ОТНОСИТЕЛЬНО РИСКОВ.
Для
применения критерий Лапласа относительно рисков по исходной платежной матрице
строится матрица рисков R = {Rij}(mxn).
Показателем эффективности LRi
стратегии Ai по критерию Лапласа относительно рисков называется среднее
значение рисков, расположенных в i-й строке матрицы рисков {Rij}:
LRi =
(1/n)∙∑ Rij, 1≤j≤n; i=1, …, m. (24)
Оптимальной будет стратегия с
минимальным значением среднего риска:
LR = min
LRi; 1≤i≤m. (25)
Чистая стратегия Ak игрока A
будет оптимальной стратегией, если LRk = LR.

ПРИМЕР 7. (ВЫБОР ОПТИМАЛЬНОЙ СТРАТЕГИИ ПО КРИТЕРИЮ ЛАПЛАСА
ОТНОСИТЕЛЬНО РИСКОВ).
Найдем оптимальную стратегию в условиях по критерию
Лапласа относительно рисков для игры «с природой», заданной матрицей
эффективности (рисунок 15).
РЕШЕНИЕ. Вычислим средние риски:
LR1
= 1/3(55+50+0) = 105/3;
LR2
= 1/3 (10+65+10) = 85/3;
LR3
= 1/3 (45+0+20) = 65/3;
LR4
= 1/3 (0+75+5) = 80/3.

Вывод: оптимальной стратегией по
критерию Лапласа относительно рисков является стратегия A3.
КРИТЕРИЙ
ХОДЖА-ЛЕМАНА.
Этот критерий опирается
одновременно на критерий Вальда и критерий Байеса.
Пусть Wi
= min aij - показатель эффективности
стратегии Аi по критерию Вальда. Пусть Bi - показатель эффективности стратегии Аi по
критерию Байеса. Показатель эффективности стратегии Ai по критерию Ходжа-Лемана
определяется по формуле:
HLi = (1-h) Wi + h Bi; i=1, …, m, (26)
где 0≤
h
≤
1.
То есть показатель эффективности HLi чистой
стратегии Аi равен:
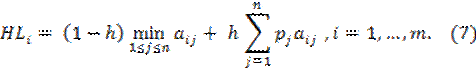
В правой
части формулы (26) коэффициент h
есть количественный показатель степени доверия игрока А данному распределению вероятностей pj= p(Qj), j=1,…,n, состояний природы Qj, j=1,…,n, а коэффициент (1– h) характеризует количественно
степень пессимизма игрока А. Чем больше доверия игрока А данному распределению
вероятностей состояний природы, тем меньше пессимизма и наоборот.
Если доверие велико, то доминирует критерий Байеса, в противном случае –
критерий Вальда.
Цену
игры HL
по критерию Ходжа-Лемана находим по формуле:
HL = max HLi, 1≤i≤m. (27)
Оптимальной
стратегией по критерию Ходжа-Лемана является стратегия Аk с наибольшим
показателем эффективности: HLk=
HL.

Отметим,
что критерий Ходжа-Лемана является как бы промежуточным критерием между
критериями Байеса и Вальда.
При h=1, из (26) имеем: HLi=Bi, и потому критерий Ходжа-Лемана превращается в критерий Байеса.
А при h=0,
из (26): HLi=Wi, и, следовательно, из критерия Ходжа-Лемана
получаем критерий
Вальда.
Выбор параметра h
субъективен, так как определить степень достоверности какой-либо
функции распределения довольно сложно.
В КАКИХ СИТУАЦИЯХ
ОПРАВДАНО ПРИМЕНЕНИЕ КРИТЕРИЯ ХОДЖА– ЛЕМАНА?
Для применения критерия Ходжа -
Лемана желательно, чтобы ситуация в которой принимается решение, удовлетворяла
свойствам:
- вероятности появления состояния Qj
неизвестны, но некоторые предположения о распределении вероятностей возможны;
- принятое решение теоретически
допускает бесконечно много реализаций;
- при малых числах реализации
допускается некоторый риск.
КРИТЕРИЙ ГЕРМЕЙЕРА.
Показатель
эффективности GWi стратегии Аi по критерию Гермейера определяем по формуле:
GWi
= min pj∙aij; 1≤j≤n; i=1, …, m. (28)
Если
игрок А придерживается стратегии Аi, то вероятность
выигрыша aij при этой стратегии и при состоянии природы Qj равна, очевидно,
вероятности pj этого состояния природы. Поэтому формула (28) показывает, что
показатель эффективности GWi стратегии Аi по критерию Гермейера есть
минимальный выигрыш при этой стратегии с учетом его вероятности.
Цена
игры по критерию Гермейера определяется по формуле:
GW = max GWi; 1≤i≤m. (29)
Оптимальной
стратегией по критерию Гермейера считается стратегия Аk с наибольшим
показателем эффективности: GWk= GW.

МАТРИЦА ГЕРМЕЙЕРА.
Умножая каждый выигрыш aij, i = 1,
…, m, на вероятность pj состояния природы Qj получим элементы матрицы
Гермейера: элемент gij = pj·aij, i = 1, …, m, j = 1, …,
n. Из элементов gij формируем
матрицу Гермейера G.
|
Состояния «природы» Стратегии
игрока A |
Q1 |
Q2 |
… |
Qn |
|
p1 |
p2 |
… |
pn |
|
|
A1 |
G11 =
p1 a11 |
G12 =
p2 a12 |
… |
G1n =
pn a1n |
|
A2 |
G 21 =
p1 a21 |
G22 =
p2 a22 |
… |
G2n =
pn a2n |
|
… |
… |
… |
… |
… |
|
Am |
Gm1 =
p1 am1 |
Gm2 =
p2 am2 |
… |
Gmn =
pn amn |

Рисунок 17. Матрица Гермейера G.
С учетом введенных обозначений числа Gi = min gij, (j = 1,..., n) являются
показателями эффективности стратегии Aj по критерию Гермейера. Таким
образом, критерий Гермейера можно интерпретировать как критерий Вальда,
применимый к игре с «ПРИРОДОЙ» с матрицей Гермейера Gij (mxn).
Критерий
Гермейера так же,как и критерий Вальда является критерием крайнего пессимизма
игрока А, но, в отличие от критерия Вальда, игрок А, принимая решение с максимальной
осмотрительностью, учитывает вероятности состояний природы.
КАКОВЫ УСЛОВИЯ
ПРИМЕНИМОСТИ КРИТЕРИЯ ГЕЙМЕЙЕРА?
Условия применимости критерия Геймейера таковы:
-
вероятности появления состояний Qj известны;
- с
появлением тех или иных состояний Qj, отдельно или в комплексе, необходимо считаться;
-
допускается некоторый риск;
- решение
может реализоваться один или много раз.
Если
функция распределения известна не очень надежно, а числа реализаций малы, то,
следуя критерию Геймейера, получают, вообще говоря, неоправданно большой риск.
Таким образом, здесь остается некоторая свобода для субъективных действий.
ЗАМЕЧАНИЕ. В случае равномерного
распределения вероятностей состояний природы: pj=1/n,
j=1,…,n, показатель эффективности стратегии Аi, в силу формулы (28),
будет равен
GWi= (1/n)∙min aij, 1≤j≤n; i=1, …, m.
Следовательно,
критерий Гермейера в этом случае эквивалентен критерию Вальда. То есть
стратегия, оптимальная по критерию Гермейера, в случае, когда мы считаем все состояния природы Qj
равновероятными, оптимальна
и по критерию Вальда, и наоборот.
КРИТЕРИЙ
ПРОИЗВЕДЕНИЙ (С УЧЕТОМ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ
«ПРИРОДЫ»).
Пусть
матрицей выигрышей игрока А является матрица А, все элементы которой
положительны: aij>0, i=1,…, m;
j=1,…, n.
Известны
вероятности pj=p(Qj), j=1,…,n, состояний природы Qj, j=1,…, n, и удовлетворяют
условию (*).
Показатель
эффективности стратегии Аi по критерию произведений (с
учетом вероятностей состояний «природы») определим по формуле:
PGi = ∏ pj aij = ∏ gij , где gij — элемент матрицы
Гермейера.
Цена
игры по критерию произведений вычисляется по формуле:
PG = max
PGi.
Оптимальной
стратегией по критерию произведений является стратегия Аk с наибольшим
показателем эффективности:
PGk=PG.

Отметим,
что для критерия произведений является существенным положительность всех
состояний вероятностей состояний природы и всех выигрышей игрока А.
МАКСИМАКСНЫЙ КРИТЕРИЙ С УЧЕТОМ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ
«ПРИРОДЫ».
Теперь опишем максимаксный
критерий, применяемый к матрице Гермейра, который для краткости будем называть
MG-критерием.
Максимаксный критерий, применяемый к матрице Гермейера можно назвать
максимаксным критерием с учетом вероятностей
состояний «ПРИРОДЫ».
Наибольший элемент в i-й строке
матрицы Гермейра G:
MGi = max
gij (j=1, …, n)
назовем показателем эффективности
стратегии Ai по MG-критерию
(или MG-показателем
эффективности стратегии Ai ).
Наибольший из MG-показателей
эффективности стратегий:
MG = max
MGi (i = 1, …, m)
назовем ценой игры по MG-критерию
(или MG-ценой
игры).
Получим:
MG
= max max gij (30)
В соответствии с этим равенством
M-цену игры можно назвать
также максимаксом матрицы Гермейера
G.
Из равенства (30) очевидно, что MG-цена
игры является максимальным элементом среди всех элементов матрицы Гермейера G.
Оптимальной по MG-критерию
назовем стратегию Ak , MG-показатель
эффективности которой совпадает с MG-ценой игры: MGk = MG.

Каждая стратегия, в соответствующей
строке матрицы Гермейера G которой стоит максимальный элемент, будет MG-оптимальной.
КРИТЕРИЙ
БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С УЧЕТОМ ОТНОСИТЕЛЬНЫХ ЗНАЧЕНИЙ ВЕРОЯТНОСТЕЙ
СОСТОЯНИЙ ПРИРОДЫ.
Предположим,
что вероятности состояний природы нам неизвестны, но мы имеем представление о
том, какие состояния природы более правдоподобны, какие — менее правдоподобны.
Это позволит представить (проранжировать) неизвестные вероятности состояний
природы в виде убывающей или возрастающей числовой последовательности.
Например,
можно считать, что последовательность неизвестных вероятностей pj состояний
природы Qj пропорциональна членам некоторой
монотонной последовательности положительных чисел t1 , t2 , ..., tn :
p1 : p2 :
... : pn = t1 : t2 : ... : tn .
Учитывая,
что ∑pj = 1; 1≤j≤n;
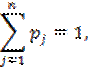
можем
получить следующие оценки вероятностей:
pj = tj/(∑tk), 1≤k≤n;
j=1,…,n. (31)
![]()

ПРИМЕР
8. (ВЫБОР ОПТИМАЛЬНОЙ СТРАТЕГИИ ПО КРИТЕРИЮ БАЙЕСА ОТНОСИТЕЛЬНО ВЫИГРЫШЕЙ С
УЧЕТОМ ОТНОСИТЕЛЬНЫХ ЗНАЧЕНИЙ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ ПРИРОДЫ).
Найдем
оптимальную стратегию в условиях (рисунок 15),
если есть основания считать, что вероятности состояний природы образуют
строго убывающую числовую последовательность, пропорциональную убывающей
арифметической прогрессии 3, 2, 1, то есть:
p1 : p2 :
p3 = 3 : 2 : 1 .
Решение.
Вычислим оценки вероятностей состояний природы по формуле (31):
p1 = 1/2, p2 = 1/3 , p3 = 1/6.
Тогда
средние выигрыши Vi будут равны:
V1 = 35/2 + 45/3 + 50/6 = 245/6;
V2 = 80/2 + 30/3 + 40/6 = 340/6;
V3 = 45/2 + 95/3 + 30/6 = 355/6;
V4 = 90/2 + 20/3 + 45/6 = 355/6.

Следовательно,
игроку A можно порекомендовать сделать
выбор между стратегиями А3 и A4 с максимальными средними выигрышами.
ЗАМЕЧАНИЕ. Аналогичный критерий
можно рассмотреть и для матрицы рисков.
КРИТЕРИЙ
МИНИМИЗАЦИИ СРЕДНЕГО КВАДРАТИЧНОГО ОТКЛОНЕНИЯ В УСЛОВИЯХ РИСКА.
При
принятии решений в условиях риска можно применить и критерий, основанный на
применении среднего квадратичного отклонения — критерий минимизации среднего
квадратичного отклонения (вариации).
Вычислим математические ожидания выигрышей игрока A при применении им чистой
стратегии Ai
на примере (рисунок 15).
B1 = p1∙
a11+ p2∙ a12 + p3 ∙a13 = 0,15 ∙ 35 + 0,35 ∙ 45 + 0,50 ∙ 50 = 46;
B2 = p1∙
a21+ p2∙ a22 + p3 ∙a23 = 0,15 ∙ 80 + 0,35 ∙ 30 + 0,50 ∙ 40 = 42,5;
B3 = p1∙
a31+ p2∙ a32 + p3 ∙a33 = 0,15 ∙ 45 + 0,35 ∙ 95 + 0,50 ∙ 30 = 55;
B4 = p1∙
a41+ p2∙ a42 + p3 ∙ a43 = 0,15 ∙ 90 + 0,35 ∙ 20 + 0,50 ∙ 45 = 43;

Следовательно,
по критерию Байеса предпочтения игрока A можно проранжировать так:
A 3 » A 1
» A 4 » A 2 .

Вычислим
средние квадратичные отклонения выигрышей:
S1 2 = 35 2
× 0,15 + 45 2 × 0,35 + 50 2 × 0,5 – (46) 2 =
2142,5 – 2116 = 26,5 ; S1 ≈ 5,15;
S2 2 =
80 2 × 0,15 + 30 2 × 0,35 + 40 2 × 0,5 – (42,5) 2 = 2075 – 1806,25 = 268,75 ,
S2 ≈ 16,4;
S3 2
= 45 2 × 0,15 + 95 2 × 0,35 + 30 2 × 0,5 – (55) 2 = 3912,5 –3025 =
887,5, S3 ≈ 29,8;
S4 2
= 90 2 × 0,15 + 20 2 × 0,35 + 45 2 × 0,5 – (43)
2 = 2367,5 – 1849 = 518,5
, S4 ≈ 22,77.

Таким
образом, по критерию минимизации среднего квадратичного отклонения, получаем:
A1 » A 2 » A 4 » A 3 .

То есть наиболее
предпочтительной является стратегия A 1 с наименьшим значением (5,15) среднего
квадратичного отклонения. Данная ситуация наиболее характерна для задач
принятия решений, когда стратегия, наиболее предпочтительная по критерию
максимизации среднего выигрыша, наименее выгодна по критерию минимизации
среднего квадратичного отклонения. Таким образом, в данных условиях игроку A предстоит сделать выбор между двумя стратегиями A1
и A3 , один из которых (A3) характеризуется и большим средним выигрышем и
большим риском одновременно.
КАК
ОПРЕДЕЛЯЕТСЯ КОЭФФИЦИЕНТ ВАРИАЦИИ?
Когда
стратегия, наиболее предпочтительная по критерию максимизации среднего
выигрыша, наименее выгодна по критерию минимизации среднего квадратичного
отклонения, то в этом случае можно порекомендовать использование особой меры риска —
коэффициента вариации:
CV ( Ai ) = CVi = (Si/Bi)∙100% .

Этот
коэффициент отражает риск, который приходится на единицу выигрыша (доходности),
и дает базу для сравнения стратегий игрока, когда и их средний выигрыш и их
средний риск неодинаковы.
В данных
условиях можно получить:
CV1 =
(5,15/46) ´ 100% = 11,2 % ;
CV2 =
(16,4/42,5) × 100% = 38,6 % ;
CV3 =
(29,8/55) ´ 100% = 54,2
% ;
CV4 = (22,77/43) ´ 100% = 53 % .

Следовательно,
по критерию минимизации коэффициента вариации, предпочтения игрока можно
проранжировать так:
A 1 » A 2 » A 4 » A 3.
То есть
наиболее предпочтительной является стратегия A1 .
Заметим
также, что когда речь идет о среднем выигрыше, то речь идет о возможности
многократного повторения игры (акта принятия решений). И условность
рассмотренных выше критериев состоит в том, что требуемого количества
повторений чаще всего может и не быть.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Данилов
В.И. Лекции по теории игр. М.: Российская экономическая школа, 2001.
[2] Мушик Э., Мюллер П. Методы принятия технических решений: Пер. с нем. – М.: Мир, 1990. – 208 с., ил.

[3] Печерский
С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс. Учебное пособие.
СПб.: 2001.
[4] Фомин Г.П. Математические методы и модели в
коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы
и статистика, 2005. — 616 с: ил.
[5] Шикин Е. В. От игр к играм. Математическое
введение. Изд. 2-е, исправл. — М.: Едиториал УРСС, 2003. — 112 с.
