Теория игр. Основные понятия теории игр. Понятие игры. Классификация игр. Понятие об игровых моделях. Комбинаторные игры. Стратегические игры. Азартные игры. Антагонистические игры. Деловые игры. Дилемма заключенного. Лотерея Хофштадтера. Оптимальная стратегия игрока. Ситуация равновесия. Игра с нулевой суммой
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Теория игр
Лекция
1
Тема
лекции 1: «Основные понятия теории игр»

Разделы лекции:
1.
Понятие игры.
2.
Классификация игр.
3.
Понятие об игровых моделях.

РАЗДЕЛ 1. ПОНЯТИЕ ИГРЫ.
ЧТО ОЗНАЧАЕТ ТЕРМИН «ИГРА»?
В практической деятельности весьма
часто приходится рассматривать явления и
ситуации, в которых участвуют две (или более) стороны, имеющие различные
интересы и обладающие возможностями
применять для достижения своих целей разнообразные действия. Подобные явления и ситуации принято
называть конфликтными, или просто
конфликтами.
Например, студент приходит на экзамен,
тянет билет и... возникает конфликтная
ситуация. Действия сторон — студента и
преподавателя — различны, да и их интересы не во всем совпадают. Разбойники
делят добычу — снова конфликт.
Типичный конфликт характеризуется тремя
основными составляющими:
1) заинтересованными сторонами,
2) интересами этих сторон и
3) их возможными действиями.

Любая конфликтная ситуация, взятая из
реальной жизни, как правило, довольно сложна. Ее изучение, к тому же,
затруднено наличием многих и очень
разных обстоятельств, часть из которых ни на развитие конфликта, ни на его
исход какого-либо существенного влияния
не оказывает. В коммерческой
деятельности, например, приходится принимать решения, учитывая множество
факторов различной природы. Причем специфика коммерческой деятельности такова,
что учитываемые при принятии решений факторы нередко обладают так называемым
свойством неопределенности, поскольку нельзя заранее определить точно, каково
будет значение того или иного фактора или показателя. Отсюда следует, что и
результат принятия решения также будет обладать свойством неопределенности.
Например, объем продажи в значительной степени зависит от спроса населения на
тот или иной товар. Спрос, как известно, является величиной случайной,
следовательно, его значение имеет некоторый разброс и является точно
неопределенным.
Неопределенность значений различных
факторов приводит к тому, что рекомендации по решению проблемы не могут быть столь
же четкими и однозначными, как в случаях полной определенности. В процессе
поиска решений появляются возможные варианты решений. Поэтому принятие решения
состоит в выборе наилучшего варианта из имеющихся.
Для решения любой проблемы независимо
от ее характера существенным является вопрос: кто должен отвечать за решение проблемы?
Другими словами, должно существовать некое ответственное лицо, принимающее
решение. Это может быть директор, бухгалтер, коммерсант, заведующий секцией,
продавец и т.д. или некоторая группа лиц: комиссия, совет директоров, бригада и
т.д. Лицо, принимающее решение, — это реально существующий индивидуум (или группа),
которого не устраивает состояние дел или перспектива их будущего развития и
который имеет полномочия действовать так, чтобы это состояние изменить.
В настоящее время многие решения в
коммерческой деятельности — заказ на поставку того или иного вида товаров,
заключение договоров с поставщиками, распределение людей в учреждениях по
должностям или операциям, управление движением товаров — все же не оптимальны.
Принятие решений в этом случае является искусством и в сильной степени зависит
от субъективных качеств лица, принимающего решение. Однако в условиях широкого
развития кооперации, усложнения производственных связей с поставщиками товаров
народного потребления и, наконец, решения задач по увеличению ассортимента и
качества товаров в торговой сети и стремления к более полному удовлетворению
потребностей населения приводят к тому, что ответственность человека за последствия
принимаемых решений многократно возросла. При этом, несмотря на отсутствие
полной определенности, необходимо проводить количественный анализ и на его
основе принимать то или иное, но обоснованное решение. В настоящее время
разработаны специальные математические методы, предназначенные для обоснования
решений в условиях неопределенности. В некоторых наиболее простых случаях эти
методы позволяют найти множество решений и выбрать из них оптимальное. В более
сложных случаях эти методы дают вспомогательный материал, позволяющий глубже
разобраться в сущности явлений и оценить каждое из возможных решений с различных
точек зрения, взвесить его преимущества и недостатки и в конечном счете
принять если не единственно правильное, то по крайней мере близкое к
оптимальному решение. Следует заметить, что при выборе решения в условиях неопределенности
всегда неизбежен элемент произвола, а, следовательно, и риска. Недостаточность
информации всегда опасна, и за нее приходится платить. Поэтому в условиях
сложной ситуации необходимо представить варианты решения и их последствий в
такой форме, чтобы сделать произвол выбора менее сильным, а риск –минимальным.
Кроме того, в коммерческой деятельности
приходится принимать решения в условиях противодействия другой стороны,
которая может преследовать противоположные или иные цели, добиваться других
путей достижения цели, препятствовать теми или иными действиями или состояниями
внешней среды достижению намеченной цели. Причем эти противодействия
противоположной стороны могут носить пассивный или активный характер. В таких случаях
приходится учитывать возможные варианты поведения противоположной стороны,
ответные действия, возможную реакцию и соответственно исходы. Возможные
варианты поведения обеих сторон и их исходов для каждого сочетания альтернатив
и состояний можно представить в виде математической модели, которая называется
игрой.
Если в качестве противоположности
выступает неактивная, пассивная сторона, которая явно активно не
противодействует достижению намеченной цели, то такие игры называются играми с
«природой». Такой стороной в коммерции являются неизвестность поведения
клиентов, реакция населения на новые виды товаров, неясность погодных условий
при перевозке товаров или проведении ярмарки, недостаточная информированность о
коммерческих операциях, закупках, сделках и т.п.
В других ситуациях противоположная
сторона активно, сознательно может противостоять достижению намеченной цели. В
подобных случаях происходит столкновение противоположных интересов, мнений,
целей. Такие ситуации называются конфликтными, а принятие решений в
конфликтной ситуации затрудняется из-за неопределенности поведения противника.
Известно, что противник сознательно стремится предпринять наименее выгодные
для вас действия, чтобы обеспечить себе наибольший успех. Неизвестно, в какой
мере противник умеет оценить обстановку и возможные последствия, как он
оценивает ваши возможности и намерения. Обе стороны конфликта не могут точно
предсказать взаимные действия. Несмотря на такую неопределенность, принимать
решения приходится каждой стороне конфликта. Необходимость обоснования
оптимальных решений в конфликтных ситуациях привела к возникновению теории
игр.
Прежде всего, попробуем разобраться,
почему для обозначения конфликтных
ситуаций было выбрано именно слово «игра». Берем «Толковый словарь живого
великорусского языка» В.И. Даля (оригинальное название: «Толковый словарь живаго
Великорускаго языка Владимира Даля») и
читаем, что игра – это «забава, установленная по правилам, и вещи для того
служащие». В силу интереса, перерастающего в азарт, люди вовлекаются в игру,
надеясь на удачу, и обычно обращаются к Богу, при этом, вступая в игру, следует
иметь в виду афоризм известного писателя, автора сатирических романов Марти
Ларни: «Многие верят в Бога, но немногим верит Бог».
Именно то, что забавы многообразны – от народных и биржевых до карточных и
военных – и весьма часто протекают по
установленным правилам, и явилось, по-видимому, основной причиной превращения в
XX веке привычного каждому с детства слова «игра» в математический термин.
ЧТО ОЗНАЧАЕТ ТЕРМИН «ТЕОРИЯ ИГР»?
Теория игр — это математическая теория
конфликтных ситуаций. Основными ограничениями этой теории являются предположение
о полной «идеальной» разумности противника и принятие при разрешении конфликта
наиболее осторожного решения.
Опишем некоторые основные понятия, используемые в теории игр.
Конфликтующие стороны называются
игроками, одна реализация игры — партией, исход игры — выигрышем или проигрышем.
Развитие игры во времени происходит
последовательно, по этапам или ходам. Ходом в теории игр называют выбор одного
из предусмотренных правилами игры действия и его реализацию.
Ходы бывают личные и случайные. Личным
ходом называют сознательный выбор игроком одного из возможных вариантов действия
и его осуществление. Случайным ходом называют выбор, осуществляемый не волевым
решением игрока, а каким-либо механизмом случайного выбора (бросание монеты,
пасовка, сдача карт и т.п.).
Одним из основных понятий теории игр
является стратегия.
Стратегией игрока называется
совокупность правил, определяющих выбор варианта действий при каждом личном
ходе этого игрока в зависимости от ситуации, сложившейся в процессе игры.
Оптимальной стратегией игрока
называется такая стратегия, которая при многократном повторении игры,
содержащей личные и случайные ходы, обеспечивает игроку максимально возможный
средний выигрыш или минимально возможный средний проигрыш.

Одной из плодотворных форм воплощения
представлений об оптимальности можно считать понятие равновесия, при котором
складывается такая (равновесная) ситуация, в нарушении которой не заинтересован
ни один из игроков. Именно ситуации равновесия могут быть предметом устойчивых договоров между игроками (ни у
одного из игроков не будет мотивов к нарушению договора). Кроме того, такие
ситуации являются выгодными для каждого
игрока: в равновесной ситуации каждый
игрок получает наибольший выигрыш (разумеется, в той мере, в какой это от него зависит).
Если в игре ситуации равновесия (в
пределах отпущенных возможностей) нет,
то, оставаясь в условиях стратегий, имеющихся у игроков, мы сталкиваемся с
неразрешимой задачей. При возникновении
подобных случаев естественно ставить вопрос о
таком расширении первоначального понятия стратегии, чтобы среди
ситуаций, составленных из новых, в том или ином смысле обобщенных стратегий, заведомо нашлись бы
равновесные. Если такие обобщенные стратегии существуют, то обычно они
представляются некоторыми комбинациями исходных стратегий (при этом, естественно, предполагается, что игра
повторяется многократно). Для того,
чтобы отличать прежние стратегии от новых, первые называют чистыми, а вторые — смешанными
стратегиями.
В большинстве конфликтных ситуаций при
выборе разумной стратегии приходится принимать во внимание не один, а несколько
показателей и факторов. Причем стратегия, оптимальная по одному показателю,
необязательно будет оптимальной и по другим.
Изучение игр можно проводить с
различных точек зрения. Мы будем стремиться к
— выработке принципов оптимальности, то
есть того, какое поведение игроков следует считать разумным, или целесообразным,
— выяснению реализуемости этих
принципов, то есть установлению
существования оптимальных в выработанном смысле
ситуаций и
— отысканию этих реализаций.
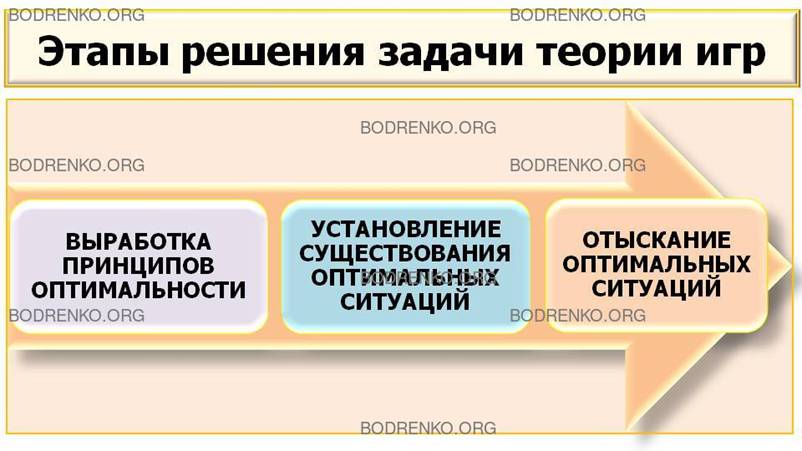
РАЗДЕЛ 2. КЛАССИФИКАЦИЯ ИГР.
В зависимости от причин, вызывающих
неопределенность исходов, игры можно разделить на следующие основные группы:
- комбинаторные игры, в которых правила
дают в принципе возможность каждому игроку проанализировать все разнообразные варианты
своего поведения и, сравнив эти варианты, избрать тот из них, который ведет к
наилучшему для этого игрока исходу. Неопределенность исхода связана обычно с
тем, что количество возможных вариантов поведения (ходов) слишком велико и практически
игрок не в состоянии их всех перебрать и проанализировать;
- азартные игры, в которых исход
оказывается неопределенным в силу влияния различных случайных факторов.
Азартные игры состоят только из случайных ходов, при анализе которых применяется
теория вероятностей. Азартными играми теория игр не занимается;
- стратегические игры, в которых полная
неопределенность исхода вызвана тем, что каждый из игроков, принимая решение о
выборе предстоящего хода, не знает, какой стратегии будут придерживаться
другие участники игры, причем незнание игрока о поведении и намерениях
партнеров носит принципиальный характер, так как отсутствует информация о
последующих действиях противника (партнера).

Существуют игры, сочетающие в себе
свойства комбинаторных и азартных игр, стратегичность игр может сочетаться с
комбинаторностью и т.д.
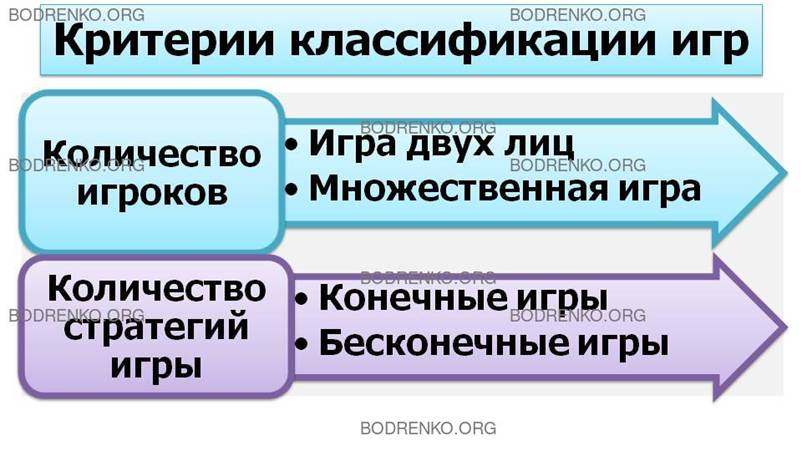
В игре могут сталкиваться интересы двух
или более игроков.
Если в игре участвуют два игрока, игра
называется парной, если число игроков больше двух – множественной. Участники множественной игры
могут образовывать коалиции (постоянные или временные). Множественная игра с
двумя постоянными коалициями превращается в парную. Парные игры получили наибольшее
распространение в практике анализа игровых ситуаций.
В зависимости от числа возможных
стратегий игры делятся на конечные и бесконечные. Игра называется конечной,
если у каждого игрока имеется только конечное число стратегий. Игра называется бесконечной, если хотя бы у
одного игрока имеется бесконечное число стратегий.
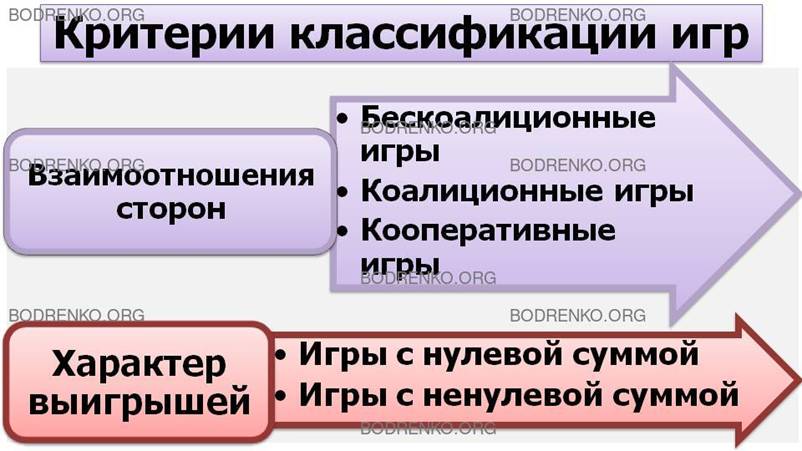
Различают игры и по сумме выигрыша.
Игра называется игрой с нулевой суммой, если каждый игрок выигрывает за счет
других, а сумма выигрыша одной стороны равна проигрышу другой. В парной игре с
нулевой суммой интересы игроков прямо противоположны.
ПАРНАЯ ИГРА С НУЛЕВОЙ СУММОЙ НАЗЫВАЕТСЯ
АНТАГОНИСТИЧЕСКОЙ ИГРОЙ.
Наиболее полно исследованы в теории игр
антагонистические игры. Игры, в которых выигрыш одного игрока и проигрыш
другого не равны между собой, называются играми с ненулевой суммой.
По количеству ходов, которые делают игроки
для достижения своих целей, игры бывают одношаговые и многошаговые. Одношаговые
игры заключаются в том, что игрок выбирает одну из доступных ему стратегий и
делает всего один-единственный ход. В многошаговых играх игроки для достижения
своих целей делают последовательно ряд ходов, которые могут оканичиваться правилами
игры либо могут продолжаться до тех пор, пока у одного из игроков не останется
ресурсов для продолжения игры.

В последнее время получили большое
распространение так называемые деловые игры. Деловая игра имитирует взаимодействие
людей и проявляется как упражнение в последовательном принятии множества решений, основанное на
некоторой модели коммерческой деятельности и на исполнении участниками игры конкретных
ролей-должностей.
Деловые игры предназначены для
воспроизведения и согласования коммерческих интересов. В основе конструкции игры
лежат взаимосвязь ресурсов и использование знаний об их возможностях. Деловые
игры имитируют организационно-экономические взаимодействия в различных звеньях
коммерческих организаций и предприятий.

Элементами игровой модели являются:
- участники игры;
- правила игры;
- информационный массив, отражающий
состояние и движение ресурсов моделируемой хозяйственной системы.
Преимущества игровой имитации перед реальным
объектом таковы:
- наглядность последствий принимаемых
решений, переменный масштаб времени;
- повторение имеющегося опыта с
изменением установок;
- переменный масштаб охвата
коммерческих явлений и объектов.
Основными направлениями использования
деловых игр являются следующие:
- учебный процесс, например обучение
моделированию коммерческих операций;
- аттестация персонала, проверка их
компетентности;
- научные исследования;
- разработка бизнес-планов.
В деловых играх игрокам обычно задаются
начальные условия, в которых они находятся, сообщаются правила проведения игры,
представляются варианты возможных решений и оценка их последствий. В игре
обязательно присутствует «ведущий», который руководит игрой, оценивает принятые
игроками решения, состояния, в которых они могут находиться в процессе игры, и
определяет выигрыши и проигрыши по исходам игры.
Приведенный перечень существующих в
настоящее время игр далеко не исчерпан. Проведение
классификации и группировки игр позволяет для однотипных игр найти общие методы
модели поиска альтернатив в принятии решения, выработать рекомендации по
наиболее рациональному образу действий в ходе развития конфликтных ситуаций в
коммерческой деятельности.
Решения, принимаемые в коммерческой
деятельности, направлены, как правило, на удовлетворение определенных потребностей
населения и связаны обычно с распределением ресурсов предприятия: товаров,
денег, людей и т.д. Основными вопросами
теории игр, которые возникают в коммерческой деятельности, являются:
1) в чем состоит оптимальность
поведения каждого из игроков в игре, какие свойства стратегий следует считать
признаками оптимальности;
2) существуют ли стратегии игроков,
которые обладали бы атрибутами оптимальности;
3) если существуют оптимальные
стратегии, то как их найти?
РАЗДЕЛ 3. ПОНЯТИЕ ОБ ИГРОВЫХ МОДЕЛЯХ.
В данном разделе мы рассмотрим наиболее
известные примеры игровых моделей.
ИГРА «ДОЛЛАРОВЫЙ АУКЦИОН».
В 1971 году Мартин Шубик (Martin Shubik) предложил игру, которая может служить моделью многих реальных ситуаций. Сущность игры заключается в следующем. Проводится аукцион, на котором предлагается один доллар, с минимальной ставкой в 1 цент. Игра проводится по обычным правилам аукционов, за исключением одного дополнения: платит не только предложивший максимальную сумму и получающий доллар, но и тот, кто платит названную им сумму, но выигрыша не получает.
Многочисленные эксперименты в разных аудиториях показали, что взрослые интеллигентные люди готовы за доллар отдать сумму, в несколько раз большую. Иррациональность такого решения очевидна, тем не менее, если участников десяток человек, игра почти всегда удается.
Игра имеет три критических момента.
Первый связан с ее запуском. Легче всего игру удается начать под общее веселое настроение. Но как только сделано два предложения, игра продолжается автоматически.
Второй критический момент связан с достижением предложения 50 центов. Теперь нужно предложить более 50 центов, и предлагающему становится ясно, что ведущий аукциона уже выиграл. Но для предлагающего повышение ставки все еще имеет финансовый смысл. Когда игроки перешли границу 50 центов, игра практически всегда бодро продолжается до 99 центов.
Третий критический момент достигается, когда кто-то готов заплатить 100 центов за доллар. При этом он, возможно, надеется завершить игру без проигрыша. Но его противник знает, что он потеряет 99 центов, если завершит игру, а если предложит 101 цент, то, возможно, проиграет лишь один цент. Он понимает, что ведет себя нерационально, но обычно игра продолжается.
В большинстве случаев в начальной стадии игры принимает участие большее число игроков, а к концу остается всегда двое. Исследования показали, что при пересечении границы в 100 центов характер игры меняется, и у игроков проявляются сильные эмоции. У них, к примеру, как у парашютистов перед прыжком, внезапно замедляется пульс.
Игра идет аналогично и в случае, когда на аукцион предлагается какой-либо предмет. И тогда находятся люди, которые готовы заплатить за него сумму, значительно превышающую его стоимость. Однако прелесть продажи именно доллара состоит в том, что здесь в явном виде предстает иррациональность решений игроков.
С помощью опросов и анкет было выяснено, что с некоторого момента у игроков меняется мотивация игры. Если в начале они хотели выиграть доллар, то в конце дело идет о престиже, доминировании и т.п.
Рассмотренный феномен в литературе называют также «Ловушка “Конкорд”». Связано это название со следующим. Затраты англичан и французов на создание сверхзвукового пассажирского самолета «Конкорд» по мере разработки резко возрастали. Еще когда затраты были не очень высоки, стало ясно, что это предприятие никогда не даст прибыли. Но правительства все глубже увязали в проекте, и к его завершению плановые суммы были многократно превышены. Даже после окончания проекта дешевле было оставить самолет как музейный экспонат, т.к. с этого момента он непрерывно приносил только убытки. Но самолет стал престижным объектом, которым англичане и французы могли гордиться, и поэтому он продолжал летать до недавнего времени.
Ситуации, соответствующие модели
долларового аукциона, встречаются на каждом шагу и в обыденной жизни. Чем
дольше мы ждем автобус, тем труднее нам сесть на такси, даже если вначале мы
были готовы поехать на такси. Чем дольше мы смотрим плохой фильм, тем вероятнее
мы досмотрим его до конца, хотя вероятность того, что в нем еще будет что-то
интересное, становится все меньше. Это обстоятельство используют на телеканалах,
включая больше рекламы в конце фильма, поскольку вероятность того, что зрители
переключатся на другой канал, будет невелика. По этой же логике проходят
забастовки. Нередко ущерб от забастовки для обеих сторон много больше, чем, если
бы сразу удовлетворить требования бастующих. В этих случаях опытный посредник
может вывести ситуацию из тупика, предложив обсудить сначала другой вопрос,
например о новой спецодежде. Этот вопрос решается быстро, после чего
противоборствующие стороны могут выйти из противостояния без потери лица.
ИГРА «ДИЛЕММА ЗАКЛЮЧЕННОГО».
Авторами «дилеммы заключенного» были Мерил Флуд (Merill Flood) и Мелвил Дрешер (Melvin Drescher). Они впервые представили ее в 1950 году. Но свое название игра получила от Альберта Такера (Albert W. Tucker) – американского математика, применившего это название на семинаре по теории игр, который он проводил в 1950 году на психологическом факультете Стэндфордского университета. С тех пор написаны тысячи статей математиками, психологами, политологами и экономистами, но и сегодня она остается такой же таинственной и поражающей. Художественная форма описания дилеммы у разных авторов может отличаться, но смысл ее остается неизменным. Ниже представлен один из вариантов.
«Полиция арестовала двух человек, подозреваемых в грабеже и убийстве. Хотя полиция уверена в их виновности, твердых доказательств для предъявления суду у нее нет. Однако у обоих подозреваемых изъяли незарегистрированное огнестрельное оружие. Следствию очень хотелось быстрее закончить это дело, и поэтому обоим было предложено содействовать следствию. Содержание предложения следователя было таким:
- если один «раскалывается» и приводит к раскрытию преступления, а другой отказывается сотрудничать со следствием, то первый немедленно освобождается, а второй получает 10 лет заключения;
- если оба признаются, то они получают оба по шесть лет заключения, т.к. ценность признания первого резко снижается;
- если оба отказываются сотрудничать со следствием, они получают по три года за незаконное владение оружием.
Каждому из задержанных сообщили, что предложение сделано обоим и действует до 10 часов утра следующего дня. Задержанные содержались в условиях, в которых они не могли общаться. Известно также, что каких-либо твердых обязательств друг перед другом у задержанных нет.»
Матрица решений для данных условий приведена в таблице 1 (рисунок 1).
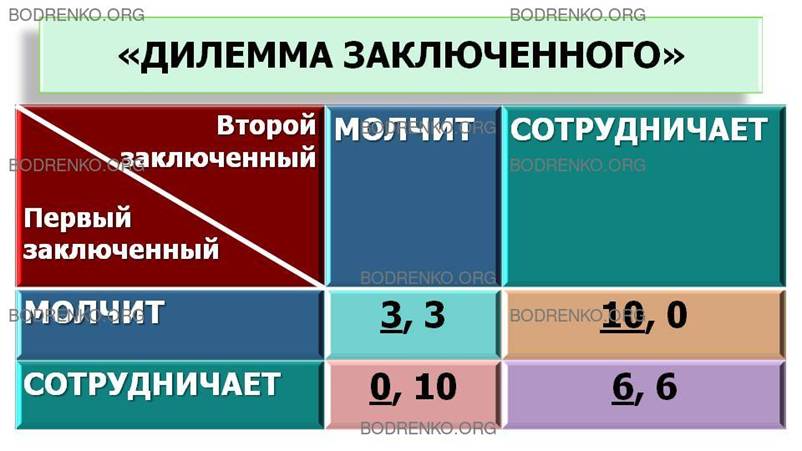
Рисунок 1. «Дилемма заключенного».
Доминантной стратегией для обоих является сотрудничество со следствием, поскольку оно может привести к немедленному освобождению. Если сотрудничает только один, то второму тоже имеет смысл сотрудничать, поскольку срок все же на четыре года уменьшается. Вроде бы, для обоих имеет смысл признаваться, и это вполне логично. Но если оба будут действовать рационально (оба признаются), и тот и другой получат большие сроки, чем, если бы действовали кооперативно (т.е. оба бы молчали). Таким образом, индивидуальная рациональность ведет к коллективной нерациональности и, как следствие, к вреду для себя самого.
В общественной жизни и в бизнесе случаев, которые сводятся к «дилемме заключенного», сколько угодно, поэтому возникает вопрос о том, как с ними поступать. Призывы вести себя кооперативно, хотя они и нужны, помогают мало. Нужны реальные санкции, контрольные механизмы, но также и рыночные льготы.
Чтобы лучше понять сущность «дилеммы заключенного», целесообразно провести ее анализ с позиций формальной логики. Итак, оба напарника не являются друзьями, их кооперация чисто случайна, они не имеют моральных обязательств по отношению друг к другу. Если встать на позицию одного из заключенных, можно проследить ход его логических рассуждений: «Если мой напарник признается, я могу либо тоже признаться и получить 6 лет, либо нет, и тогда я получу 10 лет. То есть, если мой напарник признается, мне лучше тоже признаться. Если же мой напарник не признается, у меня опять две возможности: я признаюсь, и завтра свободен, или я не признаюсь, и получаю три года. То есть, если мой напарник не признается, мне лучше признаться. Таким образом, независимо от того, какой выбор сделает напарник, мне лучше признаться». Логика диктует второму напарнику то же самое. Они оба признаются и получают по 6 лет, хотя могли бы обойтись тремя годами, если бы оба молчали. Возникают вопросы: диктует ли логика только такое поведение и исключает ли логика кооперативное поведение? Последующая цепочка рассуждений столь же логична, как и предыдущая: «Я не особенно привязан к своему напарнику, но я знаю, что интеллект его на моем уровне и он способен столь же логично рассуждать, иначе я бы с ним и не связался. Я знаю, что он в таком же сложном положении, что и я. Он тоже мне ничем не обязан и получил то же самое предложение от следователя, что и я. Он будет принимать решение, исходя из своих интересов и логики, как и я. Следовательно, мой напарник придет к тем же выводам. Поэтому, если я приду к выводу, что следует признаться, он придет к тому же выводу, и мы получим по 6 лет. Если я приду к выводу не признаваться, он тоже придет к этому выводу, и мы получим по три года. Но три года лучше, чем 6, поэтому я не буду признаваться». Возникает вопрос: в чем дело? Как могут два логичных рассуждения приводить к разному результату? Это противоречит законам логики. Внимательный пошаговый логический анализ двух приведенных рассуждений показывает, что во втором рассуждении внесено одно дополнительное соображение, а именно: рассуждения обоих заключенных неизбежно приведут их к одинаковому выводу независимо от того, кто его делает. Но это, в свою очередь, означает, что «дилеммы заключенного» просто не может быть. Обычная логика не содержит указанного дополнительного условия. Поэтому в ситуации «дилеммы заключенного» кооперативное поведение обоих заключенных исключается.
Предательство и конкуренция в нашей жизни не исключаются, и на каждом шагу приходится с ними считаться. Однако это обстоятельство не исключает существование миров (систем), в которых «дилеммы заключенного» просто не может быть (например, в мире, абсолютным законом которого является Золотое Правило нравственности или Категорический императив Канта). По нашим нынешним меркам такой мир утопичен, но в таком мире, вероятно, было бы хорошо жить.
По модели «дилеммы заключенного»
развивается и спираль гонки вооружений. Равновесие двух противников может быть
обеспечено как в случае, когда обе стороны вооружены до зубов, так и на
существенно более низком уровне, что гораздо дешевле. Поэтому такой вариант
является для обеих сторон самым выгодным. Матрица для этого случая представлена
в таблице 2 (рисунок 2).

Рисунок 2. «Спираль гонки вооружений».
Очевидно, что для каждой стороны
превосходство лучше дешевого равновесия, а дорогое равновесие лучше
незащищенности. Однако каждая сторона стремится ни в коем случае не допустить
превосходства другой стороны, поэтому тратит все больше средств на вооружение.
Оптимальным для обеих сторон вариантом было бы дешевое равновесие, но этому
мешает отсутствие доверия.
ИГРА «ПРОБЛЕМА ОБЩЕСТВЕННОГО ВЫПАСА».
«Дилемму заключенного» со многими участниками называют также «Проблемой
общественного выпаса». Ее можно проиллюстрировать следующим примером.
Десять крестьян держат по одной корове и пасут их на общем
пастбище. Коровы упитанны и здоровы. Крестьяне становятся богаче, и
некоторые из них могут себе позволить приобрести по второй корове. Когда первый
крестьянин выгоняет на пастбище две коровы, особых изменений не видно. Может
быть, коровы чуть менее упитанны. Когда несколько крестьян заводят по второй
корове, то корма уже не хватает, и коровы становятся тощими. Ценность всех
коров, вместе взятых, становится меньше ценности первоначальных десяти коров.
Когда все десять крестьян заводят по две коровы, все стадо становится очень тощим.
Матрица решений для этого примера
имеет вид, представленный в таблице 3 (рисунок 3).
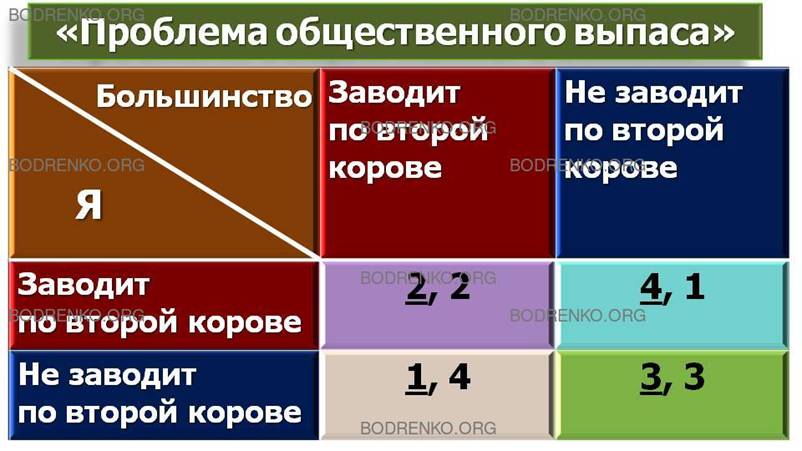
Рисунок 3. «Проблема общественного выпаса».
Каждый отдельный владелец скота действовал в пределах нормы, однако индивидуальное легитимное поведение привело к катастрофе. Такие ситуации характерны для многих экологических проблем.
«ДИЛЕММА ЗАКЛЮЧЕННОГО» ДЛЯ СЛУЧАЯ ИГРЫ СО МНОГИМИ ХОДАМИ.
Американский политолог Роберт Аксельрод теоретически исследовал вопрос о том, может ли в индивидуалистском мире развиться кооперация. Для этого он в 1979 году предложил ряду известных ученых принять участие в соревновании компьютерных программ с решением «дилеммы заключенного» в случае многих ходов. Каждая программа должна была сделать 200 ходов против каждой другой программы. Результаты обрабатывались в соответствии с матрицей, представленной в таблице 4 (рисунок 4).
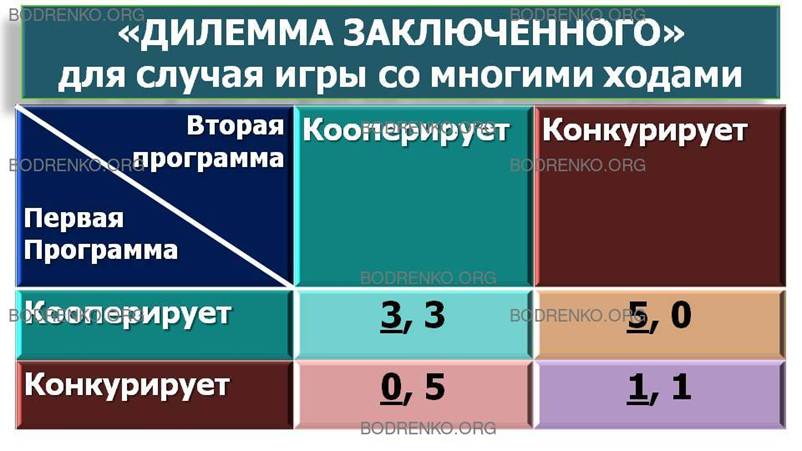
Рисунок 4. «Дилемма заключенного» для случая игры со многими ходами.
Победа присуждалась программе, получившей максимальное суммарное число очков. В турнире участвовало 15 программ.
Победила программа известного специалиста по социальной психологии Анатолия Рапопорта. Рапопорт назвал свою программу «Tit for Tat» («Зуб за зуб»). В литературе по теории игр ее обозначают TFT. Ее алгоритм был очень прост:
1. Сотрудничай в первом круге.
2. Делай то, что сделал твой противник в первом круге.
Аксельрод проанализировал все программы и пришел к выводу, что для лучших программ были характерны два признака: дружелюбие и снисходительность. Аксельрод называл программу дружелюбной, если она никогда не начинала конкурировать первой. Снисходительной он называл программу, если она после противостояния была готова возвратиться к кооперированию, как только противник начинал кооперировать.
В 1982 году Аксельрод вновь объявил конкурс программ, в котором приняли участие 62 программы из шести стран и восьми научных дисциплин. Все участники были знакомы с результатами предыдущего турнира и соответствующим анализом Аксельрода.
Анатолий Рапопорт вновь отправил свою простую программу, и вновь неожиданно для всех она оказалась победителем. Аксельрод проанализировал все присланные программы и установил, что кроме двух вышеназванных признаков еще три признака характерны для лучших программ: степень провоцируемости, взаимность и простота. Под «степенью провоцируемости» Аксельрод понимал то, что на конкурирующее поведение противника программа с большой вероятностью отвечает конкурентно. Под «взаимностью» понимается то, что реакция программы сильно зависит от стратегии противника. Наконец, «простоту» программы Аксельрод характеризовал длиной программы. Стратегия TFT в наибольшей степени удовлетворяет всем пяти признакам. Важнейшим результатом исследований Аксельрода является то, что теоретически установление стабильного кооперирования даже в тотально эгоистическом окружении не исключается. Все программы были ориентированы на выигрыш и руководствовались исключительно эгоистическими соображениями, а не альтруизмом или сложными моральными принципами. Если у живого существа разовьется ген TFT (или, по крайней мере, пять вышеназванных характеристик), оно способно к кооперации даже в условиях, когда его цели полностью эгоистичны.
Многочисленные эксперименты с «дилеммой заключенного» дали ученым интересные данные о поведении людей и о принятии ими решений. При однократной игре примерно в 40% случаев пары ведут себя кооперативно. Л. Меро по этому поводу пишет, что этот результат в зависимости от своих собственных взглядов можно воспринимать двояко:
1. К счастью, кооперация не такая уж редкая вещь, даже если логика диктует иное поведение.
2. К сожалению, слишком мало людей ведут себя в соответствии с общим интересом.
Изменения чисел в матрице, изменяющее и соотношение оптимума и наибольшего ущерба, меняло долю случаев кооперации. Возможность общения партнеров также меняла долю случаев кооперации, но не так сильно, как можно было бы предположить (она возрастала с 40% до 50% случаев). Мужчины при многократном повторении игры приходили к заметно большей доле кооперации (до 60%), чем женщины (менее 35%). Последнее обстоятельство становится особенно интересным, если его сравнить с ситуацией «долларового аукциона». Мужчины в «долларовом аукционе» позволяют гораздо больше втягивать себя в соперничество, чем женщины.
ИГРА «СЕМЕЙНЫЙ СПОР».
Проблема заключается в следующем. Молодая семейная пара утром
ссорится по поводу того, как они проведут вечер. Муж предлагает пойти на финал
соревнований по боксу, в то время как жена предлагает пойти на концерт.
Поскольку они торопятся на работу, они не успели договориться, и в течение дня
у них тоже не было возможности пообщаться. Оба заканчивают работу незадолго до
начала соревнований и концерта. Поэтому они должны независимо друг от друга
определиться, куда каждый из них пойдет.
Чтобы эта проблема могла быть проблемой теории игр, оба игрока
должны иметь ясные предпочтения. Наша пара их имеет. Прежде всего, они хотели бы вечер провести вместе. Это
имеет для них наибольшую ценность. На втором месте по важности у них стоит
предпочтение мероприятия. Наихудший вариант для них, если они вечер проведут
раздельно, причем жена будет на соревнованиях по боксу, а муж на концерте.
Несколько лучше они оценивают вариант раздельного проведения вечера, когда он
идет на бокс, а она – на концерт. С наибольшим удовольствием жена пошла бы с
мужем на концерт (вариант оценивается в 4 балла), несколько хуже для нее
посещение соревнования по боксу (3 балла). Для мужа ситуация прямо
противоположна. Матрица решений представлена в таблице 5 (рисунок 5).
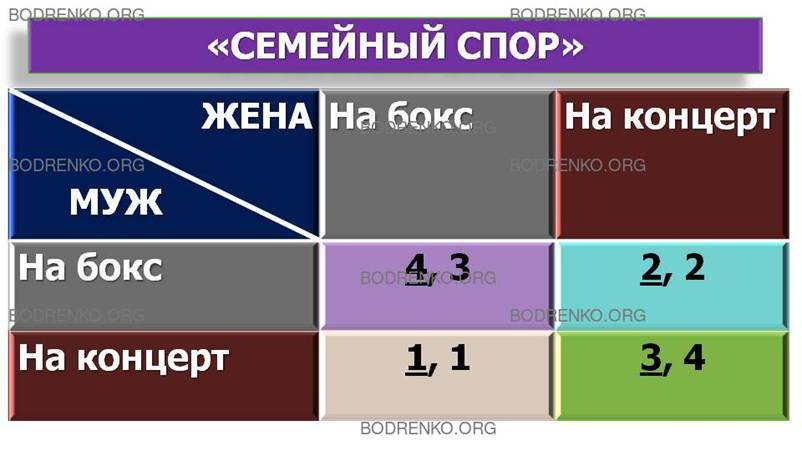
Рисунок 5. «Семейный спор».
Рассмотрим решение этой дилеммы при применении правил этики.
Вначале рассмотрим решение в случае применения «Золотого правила нравственности» в формулировке Конфуция: «Не делай другим того, чего не желаешь себе». В этом случае жена должна пойти на бокс, поскольку это хорошо для ее партнера. Ее партнер соответственно пойдет на концерт, и в результате реализуется наихудший вариант.
Если мы применим категорический императив Канта: «Поступай только согласно такой максиме (правилу), руководствуясь которой ты в то же время можешь пожелать, чтобы она стала всеобщим законом», то мы придем к следующим результатам. Асимметричные случаи здесь исключаются по определению. Остаются две возможности, и в обоих «для меня» (как для мужа, так и для жены) лучше следовать эгоистической стратегии. Следовательно, категорический императив предписывает мужу пойти на бокс, а жене – на концерт. Это действительно лучше, чем результат, полученный за счет применения «Золотого правила», но далеко от оптимального варианта.
ИГРА «ВОЖАК».
Примером игры «Вожак» может служить
ситуация, когда двое чрезмерно вежливых людей хотят пропустить друг друга
вперед. Конкурирующая стратегия здесь заключается в том, чтобы другого обязательно
пропустить вперед. Матрица решений представлена в таблице 6 (рисунок
6).
Дадим следующие пояснения. Если оба
человека конкурируют, то им никогда не пройти в дверь (1, 1). Несколько лучше
ситуация, когда они оба кооперируют (сдаются) и пытаются пройти в дверь
одновременно (2, 2). Они решат задачу, но могут оказаться несколько помятыми.
Если же один из них кооперирует, то есть берет на себя функцию быть не столь вежливым,
то они оба быстро проходят через дверь. При этом конкурирующий субъект имеет
преимущество, поскольку может считать первого невежливым (3, 4).
|
2 1 |
Кооперирует |
Конкурирует |
|
Кооперирует |
2, 2 |
3, 4 |
|
Конкурирует |
4, 3 |
1, 1 |

Рисунок
6. «Вожак».
ИГРА «ЦЫПЛЕНОК».
Игра «Цыпленок» (Chicken) получила свое название от игры молодежных банд в Лос-Анджелеса, сущность которой сводилась к следующему. Молодые люди на украденных автомобилях с высокой скоростью ехали навстречу друг другу. Тот, кто первым отворачивал, получал прозвище «цыпленок» и считался «трусливым зайцем». Итог игры в значительной степени зависит от того, насколько в исходном состоянии один из игроков смог показать другому, что он ни в коем случае не будет сворачивать. Тогда другому ничего не остается, как отступать, чтобы избежать лобового столкновения. Наилучшая стратегия в этой игре – кооперировать, если второй конкурирует, и наоборот. Матрица решений представлена в таблице 7 (рисунок 7).
|
2 1 |
Кооперирует |
Конкурирует |
|
Кооперирует |
3, 3 |
2, 4 |
|
Конкурирует |
4, 2 |
1, 1 |
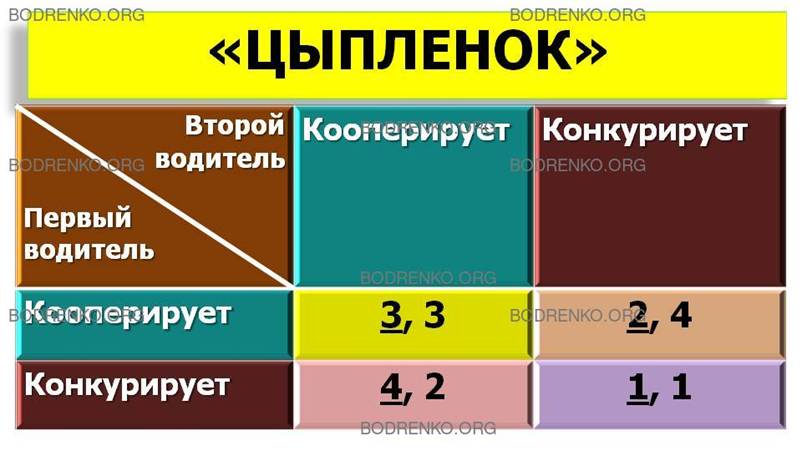
Рисунок
7. «Цыпленок».
В некоторых случаях противники находятся в неравном положении или отличается порядок их предпочтений. Так, например, в игре «Семейный спор» мужчина может о пропуске матча по боксу сожалеть несколько больше, чем женщина о пропуске концерта. Это несколько изменяет результаты игры, но основные механизмы остаются без изменений. Однако могут быть случаи, когда интересы игроков радикально различаются, и тогда даже оценка ими событий (результатов) может быть различной. Может оказаться, что один из них воспринимает ситуацию, как игру «Цыпленок», а другой – как «Дилемму заключенного».
ИГРА «ЛОТЕРЕЯ
ХОФШТАДТЕРА».
Дуглас Хофштадтер (Douglas R. Hofstadter) предложил читателям журнала «Scientific American» следующую игру. Читатель мог получить один миллион долларов, прислав заявку в редакцию журнала, если бы он оказался единственным, кто откликнулся. Если бы их оказалось двое, то выигрыш был бы вдвое меньше, и сумма была бы разыграна между ними, но получал бы только один. При трех заявках разыгрывалась бы сумма в 333333,33 доллара. При миллионе участников один бы выиграл один доллар. В обычных лотереях увеличение числа участников также снижает вероятность получения выигрыша отдельным участником, однако выигравший получает полную сумму. Но в «лотерее Хофштадтера» каждый участник «портит» игру, т.е. принимать участие как бы неэтично. Но если никто не примет участие, то в целом читатели проигрывают журналу и лишают себя великолепного шанса стать миллионером. Игра относится к категории «социальных ловушек».
Примером реальной ситуации может служить небольшой город, в котором нет такси. Если появляется несколько таксистов, они могут хорошо зарабатывать и даже разбогатеть. Но как только другие водители увидят такую благоприятную возможность и включатся в этот бизнес, то через некоторое время ни один не сможет таким образом зарабатывать себе на жизнь. Проблему могут урегулировать городские власти, ограничивая число разрешений на занятие этим бизнесом. Игры такого типа могут служить моделью для изучения оптимального использования природных ресурсов.
Для разрешения патовой ситуации в «лотерее Хофштадтера» математики предложили следующий подход. Предположим, что 100000 человек прочитали объявление о лотерее в журнале и подумали, принять участие в лотерее или нет. Тем самым они автоматически стали участниками лотереи. Мысленно представим себе игральную кость со 100000 граней, которую каждый участник лотереи метает один раз. Если выпадет цифра 1 (или любая другая заранее согласованная), читатель должен направить заявку в журнал, если выпадает любая другая цифра, читатель не направляет заявку. Таким образом, каждый читатель принимает участие в лотерее с равной вероятностью, и каждый принимает решение по одному и тому же принципу. Поэтому никого нельзя обвинить в неэтичном поведении. Возможно, что в результате окажется только один заявитель, который и станет обладателем приза. Очевидно, что существует определенная вероятность того, что цифра 1 при ста тысячах метаний не выпадет ни разу или выпадет более одного раза. В первом случае читатели полностью проигрывают журналу, во втором случае выигрыш окажется меньше максимально возможного. В природе случайность решения обеспечивается многообразием. Роль игральной кости берут на себя генетические, квантово-механические, экономические и психологические механизмы. У конкретных людей роль игральной кости играют настроение, сомнения, которые спонтанно меняют наши взгляды и подходы.
Оптимальное решение как для «лотереи Хофштадтера», так и для случая «долларового аукциона», а также во многих других играх заключается в применении смешанной стратегии, понятию, введенному Джоном фон Нейманом.
Чистые стратегии в «лотереи Хофштадтера» могут быть сформулированы так: стратегия A1: «Я всегда принимаю участие в лотереях»; или стратегия A2: «Я никогда не принимаю участие в лотереях». Сущность в применении смешанной стратегии заключается в том, что человек принимает участие в лотерее с определенной вероятностью, что он реализует, например, с помощью метания игральной кости.
ИГРА «СКРЫТАЯ ЛОТЕРЕЯ: 6 ИЗ 49».
Эта игра предложена венгерским математиком и психологом Л. Меро. Суть этой игры заключается в следующем. В таблице 8 (рисунок 8) необходимо отметить 6 цифр. Победителем является тот, у кого будет минимальное количество общих с другими участниками цифр.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
29 |
30 |
31 |
32 |
33 |
34 |
35 |
|
36 |
37 |
38 |
39 |
40 |
41 |
42 |
|
43 |
44 |
45 |
46 |
47 |
48 |
49 |
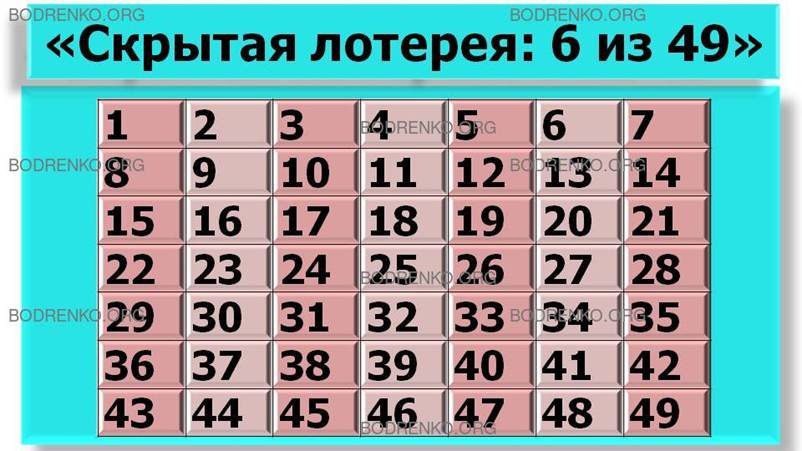
Рисунок 8. «Скрытая лотерея: 6 из 49».
Результат игры, в которой приняло
участие 236 человек, представлен в таблице 9 (рисунок 9).
|
1 39 |
2 40 |
3 30 |
4 29 |
5 30 |
6 33 |
7 36 |
|
8 28 |
9 14 |
10 26 |
11 31 |
12 19 |
13 35 |
14 26 |
|
15 27 |
16 22 |
17 45 |
18 26 |
19 36 |
20 30 |
21 29 |
|
22 23 |
23 36 |
24 24 |
25 28 |
26 34 |
27 28 |
28 32 |
|
29 30 |
30 24 |
31 40 |
32 31 |
33 20 |
34 21 |
35 17 |
|
36 17 |
37 31 |
38 21 |
39 27 |
40 26 |
41 26 |
42 25 |
|
43 39 |
44 28 |
45 23 |
46 18 |
47 42 |
48 37 |
49 37 |
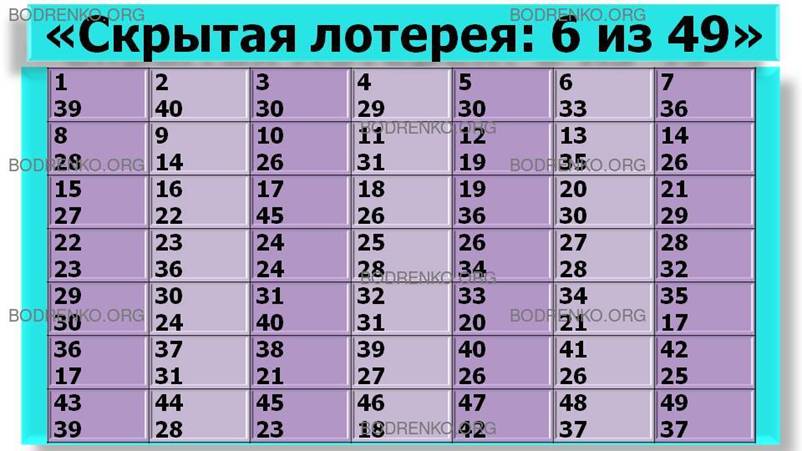
Рисунок 9. Результат игры «скрытая
лотерея: 6 из 49».
Хотя частота повторения отдельных цифр не соответствует точно случайным числам, однако и несильно от них отдалена. Многие игроки выбирали свои цифры не случайным образом, а по определенному алгоритму, который казался им наиболее рациональным. Поскольку рациональная стратегия в этой игре состоит в применении смешанной стратегии, то поведение этих отдельных игроков рациональным считать нельзя. Но коллективный результат из высших соображений (с точки зрения эволюционно стабильной стратегии) можно считать довольно рациональным. Под эволюционно стабильной стратегией понимается такая, к которой должна бы прийти популяция живых существ, чтобы обеспечить биологическое выживание. В целом при решении проблем реальной жизни приходится учитывать большое число аспектов, многие из которых ЛПР даже может не осознавать. Это ведет к еще большему многообразию подходов, сумма которых уже может приводить к оптимальным эволюционно стабильным коллективным стратегиям.
ИГРА «ПОБЕЖДАЕТ МИНИМАЛЬНОЕ ЕДИНСТВЕННОЕ ЧИСЛО».
Эта игра заключается в следующем. Журнал, в котором она была
опубликована, предлагал назвать одно целое число. Победителем должен был стать
тот, чье число оказалось минимальным и единственным, то есть не повторено ни
одним другим читателем. Было прислано 8192 ответа, которые содержали более 2000
различных чисел. Победителем оказалось число 120. Все числа меньшие 120, за исключением числа 94, которое
было названо дважды, были названы по четыре раза. Исследование присланных ответов показало, что
две трети читателей выбрали нечетные числа. Кроме того, значительно чаще
встречались числа 7, 13, 21 и некоторые другие.
Оптимальную смешанную стратегию для этой игры вычислить достаточно
сложно.
ПРИМЕР ИГРОВОЙ МОДЕЛИ.
Рассмотрим систему управления
коммерческого предприятия, структуру которого можно представить как орган
управления (дирекция) и некоторое количество производственных единиц
(товарных секций или отделов).
Каждый отдел реализует некоторый набор
товаров. В зависимости от организации и правового положения руководство может
иметь те или иные возможности управления работой отделов. Предполагается, что в
данном случае наиболее действенной формой управления является оптимальное
распределение ресурсов.
Отдел самостоятельно может выбрать
программу выполнения товарооборота. Целью коммерческого предприятия является
максимизация доходов или минимизация затрат, связанных с продажей товаров.
Сведем данную задачу к игровой модели.
Обозначим через n
число отделов; m
— число различных товарных ресурсов;
xi – вариант выполнения товарооборота,
принимаемый i-м отделом, i = 1, …, n;
yj – вид товарного ресурса, выделяемый
коммерческим директором, j
= 1, …, m;
aij
– набор товаров, реализуемый i-м отделом
при выделении j-го
вида товарного ресурса, i
= 1,…, n, j = 1,…, m;
Y - суммарный объем ресурсов, которыми
распоряжается коммерческий директор; C – доход (или потери), связанные с реализацией товара.
В терминах игровой модели можно дать
следующую интерпретацию введенных обозначений:
n - число стратегий отдела; m — число
состояний среды;
xi – i-я стратегия, i = 1, …, n;
yj
– j-е состояние среды, j= 1, …, m;
aij — исход, получаемый при стратегии xi, и состоянии
среды yj,
i
= 1,…, n, j = 1,…, m.
aij=F(xi, yj).
Математическая модель сформулированной
задачи имеет следующий вид: максимизировать (или минимизировать) величину
C (F(x1, y1), F(x1, y2), ..., F(xn,
ym)) –––>
max(min)
при ограничениях:
∑ yj = Y,
yj >= 0, j=1, …, m.

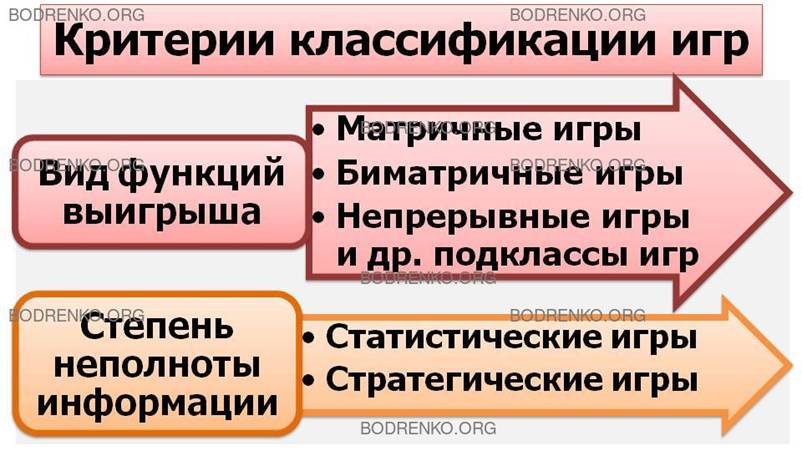
В дальнейшем мы ограничимся
рассмотрением только игр с выигрышами. На следующей лекции мы подробно
рассмотрим наиболее изученные и продвинутые классы антагонистических игр – так
называемые матричные игры. Исследование матричных игр интересно еще и потому,
что многие игры более общего вида могут быть сведены к ним приближенно. Затем
мы рассмотрим еще два вида конечных игр — позиционные игры и биматричные игры.
В заключение мы изучим игры с природой и некоторые классы бесконечных игр.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Вентцель Е.С. Элементы теории игр. М.: Физматгиз, 1961.
[2] Данилов В.И. Лекции по теории игр. М.: Российская экономическая школа, 2001.

[3] Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс. Учебное пособие. СПб.: 2001.
[4] Фомин
Г.П. Математические методы и модели в коммерческой деятельности: Учебник. —
2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.
[5] Шикин Е.
В. От игр к играм. Математическое введение. Изд. 2-е, исправл. — М.: Едиториал
УРСС, 2003. — 112 с.
