Методы SEO оптимизации

Введение

На сегодняшний день, все большее число людей предпочитают узнавать о товарах, услугах, компаниях и о многом другом через Интернет.

В сети миллиарды страниц и сотни миллионов пользователей. Поисковые системы являются естественным связующим звеном между желанием пользователя найти нужную информацию и желанием владельца сайта получить заинтересованного пользователя. Встреча двух мощных потоков спроса на информацию и предложения информации происходит в поисковых системах.

Сегодня, когда малый и средний бизнес пытается использовать интернет с выгодой для себя, руководителям предприятий, маркетологам и веб-мастерам корпоративных сайтов необходимо изучать множество вопросов, которым нет аналогов в обычной, «несетевой жизни». Нужно хорошо представлять расстановку сил на рынке сетевой навигации и следить за ее изменениями. Нужно владеть основными методами поискового продвижения. Нужно уметь оценивать собственный сайт и сравнивать его с сайтами конкурентов.

Задача поисковой оптимизации (SEO) - обеспечение максимального количества показов ссылок на продвигаемый сайт в результатах поиска по профильным запросам, с целью привлечения мотивированных посетителей на сайт по данным ключевым фразам.

Для каждой поисковой системы (Google, Yandex, Rambler, Yahoo и т.д.) существуют правила наполнения сайта содержанием, соблюдение которых помогает улучшать положение сайта в поисковых системах. Со временем правила поисковой оптимизации сайтов для различных поисковиков изменяются. Семантическое ядро - это   совокупность всех слов и словосочетаний, по которым пользователь из целевой аудитории может искать сайт. Эти слова должны быть использованы при написании содержания сайта, присутствовать в названиях и описаниях страниц. Таким образом, при наличии утвержденного списка запросов, по которым отслеживается продвижение сайта, эффективность поисковой оптимизации определяется по месту сайта в поисковой системе (в диапазоне Top100).

Цель работы – разработка и реализация в виде программы на языке Java Script алгоритма оценки эффективности поисковых запросов. Достижение этой цели позволит в перспективе повысить эффективность продвижения сайта и облегчит решение задачи формирования семантического ядра сайта.

Задачи, решаемые в ходе выполнения работы:

ü    Рассмотреть коэффициент конкордации (согласованности) как измеритель статистической связи между несколькими порядковыми переменными, где в качестве переменных использовать позиции следующих сайтов: www.rts.ru; www.prime-tass.ru; www.finmarket.ru; www.reuters.com; www.stockportal.ru; www.mfd.ru; www.businessweek.com; www.bfm.ru; www.fincake.ru ., которые они занимают в поисковых системах : Yandex.ru; Rambler.ru; Mail.ru; Google.ru; Yahoo.com; Bing.com с использованием ключевых слов, таких как: GAZR; GAZP; GMKN; LKOH; ROSN; SBER; RUB; USD; RTS.Номера позиций получаем используя сервис www.bodrenko.org .

ü    Проверить принадлежность рассматриваемых сайтов к группе финансовых сайтов;

ü    Используя полученные результаты, проанализировать сайт www.rbc.ru, и определить является ли он также финансовым.

Коэффициент конкордации (согласованности) можно рассматривать как измеритель статистической связи между несколькими порядковыми переменными. При решении основных задач статистического анализа ранговых связей возникает необходимость измерять статистическую связь между несколькими переменными. С этой целью Кендаллом и был предложен показатель, названный коэффициентом согласованности.

В заключении работы приведены основные результаты.

 

 

 

 

I глава. Основные понятия и проблемы поисковой оптимизации.

Интернет становится главным источником информации для миллионов людей. Предложение информации, и поиск информации – это услуги, за которыми стоят экономические интересы конкретных компаний.

Единицей сетевой информации является веб-страница. Но структурной единицей Интернета является множество страниц, объединенных в сайт.

Веб-сайт или просто сайт —  это совокупность документов частного лица или организации. По умолчанию подразумевается, что сайт располагается в сети Интернет. Все веб-сайты в совокупности составляют Всемирную паутину. Когда говорят «своя страничка в Интернет», то подразумевается целый веб-сайт или личная страница в составе чужого сайта.  В любой момент времени пользователь просматривает в браузере какую-то одну страницу и, переходя от одной страницы к другой, получает очередную «порцию» информации. Каждая страница в сети имеет владельца. Каждый владелец стремится получать доход от демонстрации содержимого своих веб-страниц пользователями.  Стоимость веб-страницы напрямую зависит от двух показателей – посещаемости и характеристики аудитории.

Права владения распространяются на сайты, и именно для сайтов рассчитывается посещаемость, характеристики аудитории и стоимость.

В сети миллиарды страниц. Каждая страница имеет свой уникальный адрес (URL), и ее можно просматривать, если правильно ввести URL в адресную строку браузера.

Никто не в состоянии запомнить миллиарды адресов и связанные с каждым адресом данные. Поэтому трудно представить, какова была бы Сеть без навигационных сервисов – поисковых систем и каталогов. Они дают пользователям возможность, не зная адресов, найти страницы с нужной информацией.

Но несколько адресов приходится запоминать каждому пользователю, это адреса поисковых систем и каталогов. В любой момент, зайдя на сайт поисковой системы, можно быстро переместиться на страницу с нужными данными, поэтому навигационные сервисы являются естественными распределителями потоков пользователей по страницам сети.

Для большинства сайтов именно поисковые системы являются основным источником посетителей. Это подтверждается статистикой: восемьдесят из ста новых посетителей приходят из поисковых систем и каталогов.

Таким образом, можно сказать, что поисковые системы сосредоточили на себе пользовательский спрос на информацию. И регулируют предложение информации, посылая людей на одни сайты, и не посылая на другие.

Поэтому очень важно, чтобы сайт оказался в числе тех, на которые поисковые системы отправят посетителей.

Просматривая сайты конкурирующих фирм, пользователи сравнивают альтернативные предложения. К сожалению, не все сайты способны похвастаться достаточным количеством полезной для посетителя информации. Часто вопросы пользователя, пришедшего на сайт, остаются без ответа.

Существует Зона видимости. Статистика переходов из результатов поисковых систем хорошо изучена. Из ста человек, просматривающих первую страницу с результатами поиска, на вторую переходят чуть меньше половины. Дальше третьей зайдут всего лишь пятеро. Таким образом, с вероятностью 95%  посетители нашли необходимую информацию среди первых 30 ссылок, показанных поисковой системой, либо среди рекламных предложений. Это и есть зона видимости сайта в поисковых системах.

Таким образом, складывается следующая картина:

·                   чтобы быть успешным, сайт должен выполнять свои задачи, то есть привлекать посетителей

·                   чтобы привлечь посетителей, необходимо, чтобы сайт можно было легко найти в поисковых системах

·                   чтобы сайт легко находился, он должен оказаться в зоне видимости в ответе на нужные поисковые запросы.

Достижение необходимой видимости сайта по целевым запросам возможно двумя способами: поисковая реклама и оптимизация сайта для поисковых машин.

Главное место на страницах результатов поиска занимают поисковые ссылки. Считается, что пользователи больше доверяют таким ссылкам, чем рекламе. Поисковые ссылки бесплатны. Поисковые системы не продают позиции в результатах поиска, невозможно купить ни одну из позиций в поисковой выдаче. Это принципиальная позиция поисковых систем: результаты поиска должны рассчитываться по единому для всех алгоритму, быть объективными и не зависеть от денег. Алгоритмы сортировки результатов поиска (ранжирования) являются секретом поисковых систем.

Изменяя содержимое сайта, воздействуя на эти параметры, можно продвинуть ссылки на сайт в зону видимости. Ссылки должны отображаться только по тем запросам, в ответ на которые имеется на сайте полезная для пользователя информация. Такие запросы называют целевыми. Изменение характеристик сайта для продвижения ссылок на сайт в зону видимости поисковых систем по целевым запросам называется оптимизацией сайта для поисковых машин, или поисковой оптимизацией.

Чтобы успешно оптимизировать сайт, необходимо:

·                   Уметь отбирать целевые поисковые запросы, по которым сайт будет продвигаться в поиске;

·                   Уметь оценивать эффективность продвижения;

·                   Знать методики и основные приемы поисковой оптимизации;

·                   Хорошо понимать разницу между легальными и нелегальными способами продвижения;

Главный элемент структуры современного интернета – это поисковики. Главных поисковиков очень много, но есть наиболее известные и посещаемые. Сейчас доминируют: Яндекс, Рамблер, Google, Mail. Именно поисковики упорядочивают хаос. Ведь сайты в интернете разбросаны без какого-либо порядка. Поисковая машина – это программа, которая составляет и хранит предметный указатель Интернета, а так же находит в нем заданные ключевые слова.

Один из самых важных способов поиска нужной страницы – это алфавитный список, так называемый индекс. Для составления индекса необходимо решить, какие страницы нам нужны. То есть составить список адресов, по которым будет составляться индекс. Обычно разработчики поисковой системы загружают в нее какой-то начальный список адресов страниц сайтов. Затем поисковая машина собирает все гипертекстовые ссылки с каждой из заданных страниц на другие страницы и добавляет все найденные в ссылках адреса к своему первоначальному набору адресов.

Ранжирование

Ранжированием называется упорядочение результатов поиска по их релевантности (степень соответствия запроса и найденного, то есть уместность результата) . Каждая поисковая машина имеет свою «формулу релевантности» для сайтов. В нее входит учет наличия искомых слов на странице, учет плотности этих слов по отношению к остальным словам, наличие искомых слов в особых текстовых элементах повышенной важности. Кроме того, поисковики анализируют так же позицию страницы в общем пространстве Интернета, а именно – авторитетность страницы, которую они вычисляют по количеству ссылок на нее с других сайтов.

Список запросов, по которым сайт продвигается в поисковых системах, называется семантическим ядром сайта. То есть это список поисковых запросов, наилучшим образом соответствующих смыслу, и содержанию сайта.

При составлении списка необходимо тщательно просмотреть свой сайт, сайты конкурентов и выделить все подходящие словосочетания для дальнейшей проверки;

Представить себя на месте пользователя, которому нужна предлагаемая на сайте информация;

Посоветоваться со специалистами в данной теме, и узнать наиболее устойчивые слова, используемые профессионалами.

Основной принцип составления семантического ядра следующий: в него должны входить те запросы, по которым вам есть, что предложить посетителям сайта, те, для которых на сайте есть релевантная информация. Чем больше поисковых запросов включено в семантическое ядро, тем разнообразнее варианты выбора метода оценки продвижения. Необходимо постоянно оценивать и сравнивать два показателя: видимость сайта в поисковых системах и количество посетителей, пришедших на сайт из поисковых систем.

От правильного выбора страниц, к которым стоит прилагать усилия по оптимизации, зависит количество времени и денег, которые можно потратить на поисковое продвижение. Определение наиболее релевантной страницы для каждого запроса дает возможность не конкурировать в результатах поиска со своими собственными страницами.

Даже небольшая правка текстов и элементов форматирования сайта может привести к тому, что ссылка на него окажется в зоне видимости результатов поиска. Нужно только знать какую страницу править и в каком направлении – эту информацию нам может представить таблица контент–анализа.

Поисковое продвижение сайта – это комплекс мероприятий, направленных на улучшение видимости сайта в поисковых машинах по целевым запросам. Из этого определения можно вывести три следствия. Во-первых, сначала улучшается видимость по целевым запросам. Во-вторых, видимость – измеряемая характеристика, «лучшую» видимость можно отличить от «худшей». В-третьих, количество целевых запросов должно быть конечным.

Таким образом, видимость – это оценка положения ссылок на сайт в результатах поиска по профильным запросам.

 

Существует три метода оценки продвижения сайта:

ü    Сравнение с эталоном;

ü    Подсчет количества эффективных показов;

ü    Оценка поискового трафика.

Рассмотрим метод сравнения с эталоном.

Составляя семантическое ядро, мы планируем получить результат, который хотели бы иметь прямо сейчас, то есть планируем лучший из возможных результатов. Сравнивая продвигаемый сайт с эталоном, необходимо измерять между ними связь. Для этого я предлагаю рассмотреть коэффициент конкордации (согласованности).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

II глава. Коэффициент конкордации как измеритель статистической связи между несколькими порядковыми переменными

При решении основных задач статистического анализа ранговых связей возникает необходимость измерять статистическую связь между несколькими (более чем двумя) переменными. С этой целью Кендаллом был предложен показатель Ŵ(m), названный коэффициентом конкордации, вычисляемый по формуле:

Ŵ(m)=² ,   (1)

Где m – число анализируемых порядковых переменных (сравниваемых упорядочений); n- число статистически обследованных объектов или длина ранжировки (объема выборки); k_1,k_{2, …,}k_m  - номера отобранных для анализа порядковых переменных (из исходной совокупности x⁽⁰⁾,x⁽¹⁾,x⁽²⁾,…,x^(p), так что, очевидно, m<=p+1).

Коэффициент имеет множество свойств. Рассмотрим некоторые из них. Значение коэффициента не может быть меньше 0, но и не может превышать 1. То есть 0≤ Ŵ ≤1. Ŵ =1 тогда и только тогда, когда все m анализируемых упорядочений совпадают. Чем коэффициент ближе к 0, тем менее статистически значимы обследуемые объекты.

Если m≥3 и анализируемые ранжировки генерируются подобно случайному независимому m-кратному извлечению из множества всех n! возможных упорядочений n объектов (условия гипотезы H₀), то связи между ними нет и W=0;

То, что шкала измерения W(m) не включает в себя отрицательных значений, объясняется следующим обстоятельством. В отличие от случая парных связей при анализе m (m≥3) порядковых переменных  противоположные понятия согласованности и несогласованности утрачивают прежнюю симметричность (относительно нуля); упорядочения, произведенные в соответствии с переменными x^(k1),x^(k2),….,x^(km), могут полностью совпадать, но не могут полностью не совпадать в том смысле, который мы вкладываем в это понятие при m=2.

Формула (1) получена в предположении отсутствия объединенных рангов в каждом из анализируемых упорядочений. Если же таковы имеются, то формула должна быть модифицирована:

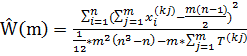    ;                                (1`)

Где поправочный коэффициент  (соответствующий переменной ) подсчитывается по формуле:

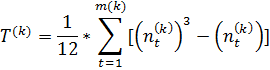
Где m^(k) – число групп неразличимых рангов у переменной х^(k) , а  - это число элементов (рангов), входящих в t-ую группу неразличимых рангов; группы неразличимых рангов, состоящие из единичного элемента не участвуют в расчете величины  .

Порядковая переменная позволяет упорядочивать статистически обследованные объекты по степени проявления в них анализируемого свойства. Таким образом, результатом измерения порядковой переменной является приписывание каждому из обследованных объектов некоторой условной числовой метки, обозначающей место этого объекта в ряду из всех n анализируемых объектов, упорядоченном по убыванию степени проявления в них к-го изучаемого свойства.

В результате измерения порядковых переменных на каждом из анализируемых объектов мы получили таблицы исходных данных .В этой таблице элемент х[i][j] задает порядковое место (ранг), которое занимает объект в ряду всех статистически обследованных объектов, упорядоченном по убыванию степени проявления j-го анализируемого свойства. Если рассмотреть столбец с номером j этой таблицы, то он будет представлять перестановку из n элементов, а именно перестановку из n натуральных чисел, определяющую порядковые места объектов (сайтов) в ряду упорядоченном по свойству. При упорядочении объектов могут встречаться ситуации, когда два или более объектов оказываются неразличимыми. Тогда каждому из объектов этой группы приписывается ранг, равный среднему арифметическому значению тех мест, которые они делят, а полученные таким образом ранги принято называть «объединенными».

Проверка статистической значимости выборочного коэффициента конкордации.

Рассмотрим, Как ведут себя выборочные значения Ŵ (m) коэффициента конкордации при повторении выборок заданного объема n (из одной и той же генеральной совокупности) при какой-либо связи между анализируемыми m переменными. Предположим, что каждому объекту конечной генеральной совокупности (состоящей из n элементов) приписан какой-то определенный ранг по каждой из m рассматриваемых переменных. Так, например, если m=3 и объекту О_i приписана тройка (x_i⁽¹⁾=N; x_i⁽²⁾=1; x_i⁽³⁾=2), то это означает, что по переменной x⁽¹⁾ он состоит на последнем (N-м) месте в упорядоченном ряду всех объектов генеральной совокупности, по переменной x⁽²⁾ – на первом и по переменной x⁽³⁾ – на втором. Тогда по исходным данным { (x_i⁽¹⁾, x_i⁽²⁾,…, x_i^(m) )}_i=1,…N с помощью формулы (1) может быть вычислен теоретический (генеральный) коэффициент конкордации W(m), характеризующий степень тесноты ранговой связи между переменными x⁽¹⁾, x⁽²⁾,…, x^(m) . Однако исследователю известны значения (x_i⁽¹⁾, x_i⁽²⁾,…, x_i^(m) ) лишь для части объектов генеральной совокупности, а именно для случайной выборки объектов объема n (n<N). После естественной перенумерации рангов, сохраняющей правило упорядочения объектов, но переводящей масштаб измерения рангов в шкалу (1,2,…,n) (для этого минимальный из оказавшихся в выборке рангов по каждой переменной объявляется рангом, равным 1, следующий по величине – рангом, равным 2, и так далее), может быть вычислен (по формуле (1)) выборочный коэффициент конкордации Ŵ (m).Извлекая другую выборку объема n из той же самой генеральной совокупности, мы получим, вообще говоря, другое значение выборочного коэффициента Ŵ (m) и так далее.

Сильно ли могут отклоняться от нуля выборочные значения коэффициента конкордации Ŵ (m) в ситуации, когда значение теоретического коэффициента конкордации W(m) свидетельствует о полном отсутствии рангов связи между анализируемыми переменными x⁽¹⁾, x⁽²⁾,…, x^(m) .

Для проверки статистической значимости анализируемой связи следует воспользоваться фактом приближенной χ² (n-1)- распределенности величины m(n-1)× Ŵ (m), справедливым в условиях отсутствия связи генеральной совокупности (Ŵ (m), как и прежде, подсчитывается по форуме (1). Поэтому, если окажется, что m(n-1) Ŵ (m)> χ_α² (n-1)

То гипотеза об отсутствии ранговой связи между переменными x^(к1), x^(к2),…, x^(кm) должна быть отвергнута (с уровнем значимости критерии, равным α); в (3) величина  χ_α² (n-1)- это 100%-ная точка χ²  распределения с (n-1)-ой степенью свободы.

Можно использовать и другой способ проверки статистической значимости исследуемой ранговой связи между несколькими переменными, основанный на том, что в условиях отсутствия таковой в генеральной совокупности распределение случайной величины  приближенно описывается Z-распределением Фишера с числом степеней свободы числителя ν₁=n-1-  и знаменателя ν₂=(m-1) ν₁ (при большом числе объединенных рангов или значительной их протяженности в расчет ν₁ и ν₂ следует ввести поправку).

Строгих рекомендаций по построению доверительных интервалов для истинного значения W в условиях наличия ранговых связей в исследуемой генеральной совокупности к настоящему времени не имеется.

Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.

Наметим некоторые подходы к решению задач, опирающиеся на понятие коэффициента конкордации.

Задача А: При анализе структуры имеющейся совокупности упорядочений (или структуру связей между исследуемыми порядковыми переменными) существенную пользу может принести решение следующей задачи:  найти разбиение анализируемого набора порядковых переменных x⁽⁰⁾, x⁽¹⁾,…, x^(р) на заданное число tнепересекающихся групп, оптимальное в смысле максимизации критерия W(t)=[W₁+ W₂+...+W_t] , где W_j –коэффициент конкордации, подсчитанный по переменным, входящим в j-ю группу. Задаваясь различными значениями t=2,3,…,t₀  (t₀<p) и прослеживая характер изменения W_опт^(t) в зависимости от t, можно добиться успеха в выявлении групп высококоррелированных переменных.

Задача В: В приложениях, особенно при статистическом анализе совокупности экспертных мнений (представленных в виде ранжировки), существенным оказывается вопрос упорядочения самих переменных (интерпретируемых, например, в качестве экспертов) по степени их коррелированности со всеми остальными переменными или с какой-то их частью (представляющей основное ядро высококоррелированных переменных). Для решения этой задачи может быть предложена следущая процедура.

Пусть W(p+1-k|x^(j1), x^(j2),… ,x^(jk)) – коэффициент конкордации, подсчитанный по всем рассматриваемым переменным x⁽⁰⁾, x⁽¹⁾,…, x^(р) за исключением переменных x^(j1), x^(j2),… ,x^(jk). Варьируя состав группы исключенных переменных, мы получим C^k_p+1 различных значений W(p+1-k). Последовательно вычислим значения всех этих коэффициентов для к=0,1,2,…,к₀ и упорядочим их (при каждом фиксированном к) в соответствии с убыванием их значений. Получим:

Ŵ (p+1);

Ŵ(p|x^(j1))≥W(p| x^(j2))≥… ≥W(p|x^(jp+1));

Ŵ(p-1| x^(q1), x^(l1))≥ Ŵ(p-1| x^(q2), x^(l2))≥… ≥Ŵ(p-1| x^(qL), x^(lL)); L=C²_p+1.

……………………………………………………………………………..

Эти упорядочения (на каждом «этаже») и дают нам одновременно ранжировки самих переменных (по одной, по паре, по тройке и так далее) по степени их согласованности с остальными переменными: очевидно, ту переменную (или ту пару, тройку и так далее переменных ) , выбрасывание которой приводит к максимальному значению меры согласованности по остальным переменным, естественно объявить наименее связанной (согласующейся) с остальными переменными.

Задача С: Если коэффициент Ŵ(m) свидетельствует о наличии статистической значимости связи между анализируемыми показателями Х^(к1), Х^(к2),… ,Х^(km), то представляет интерес задача построения оценки неизвестной «истинной» упорядоченности Х^ист рассматриваемых объектов. Эта оценка должна быть, по-видимому, результатом некоторого агрегирования имеющихся ранжировок Х^(к1), Х^(к2),…, Х^(кm). Для формирования Х^ист чаще всего используют один из трех следующих примеров:

a)                Компоненты Х^(ист) определяются в результате сравнения сумм рангов, приписываемых каждому объекту упорядочениями Х^(к1), Х^(к2),… ,Х^(km).

b)                Компоненты Х^(ист) определяются в результате сравнения выборочных медиан рангов, приписываемых каждому объекту анализируемыми упорядочениями;

c)                 «присуждение» мест объектам в упорядочении  Х^(ист) основано на «большинстве голосов», поданных за данный объект в ранжировках Х^(к1), Х^(к2),… ,Х^(km) за то или иное место; например, больше других первых мест в анализируемых ранжировках получил объект О₅, тогда ему и присуждают ранг 1 в ранжировке Х^(ист) и так далее.

Задача В совпадает с поставленной мною задачей. Решим эту задачу на языке Java script на конкретном примере.

Для реализации я выбрала именно этот язык потому, что язык JavaScript -- самый популярный в мире.

В статье "The World's Most Misunderstood Programming Language Has Become the World's Most Popular Programming Language"[18] ((рус.) этот язык программирования стал самым популярным в мире языком программирования Дуглас Крокфорд (англ.) утверждает, что лидирующую позицию JavaScript занял в связи с развитием AJAX, поскольку браузер стал превалирующей системой доставки приложений. Он также констатирует растущую популярность JavaScript, то, что этот язык встраивается в приложения, отмечает значимость языка.
По данным Black Duck Software (англ.)[21] в разработке открытого программного обеспечения доля использования JavaScript выросла. 36 % проектов, релизы которых состоялись с августа 2008 по август 2009 гг., включают JavaScript, наиболее часто используемый язык программирования с быстрорастущей популярностью. 80 % открытого программного обеспечения использует Си, C++, Java, Shell и JavaScript. При этом JavaScript единственный из этих языков, чья доля использования увеличилась (более чем на 2 процента, если считать в строках кода).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Глава III. Разработка системы анализа поисково        й оптимизации

Итак, сложим воедино то, что имеем и хотим получить.

Каждый сайт несет определенную информацию. Все сайты делятся на классы. Например, сайты могут быть экономические, юридические, научные, финансовые и т.д.

Поисковое продвижение сайта – это комплекс мероприятий, направленных на улучшение видимости сайта в поисковых машинах по целевым запросам.

Для того чтобы сайт был в зоне видимости, составляется список ключевых слов. По этим словам можно проверять и продвигать сайты в поисковых системах, тем самым оптимизируя их. То есть размещать больше ссылок на сайте с данным словом. Даже небольшая правка текстов и элементов форматирования веб-страницы может привести к тому, что ссылка на нее окажется в зоне видимости результатов поиска. Нужно только знать, какую страницу править и в каком направлении. Как правило, основные слова любого класса известны. Например, если это магазин мебели, то список слов: стул, стол, шкаф и т.д. Если это финансовый сайт, то словами могут служить названия акций.

Сайты это статистические объекты.  Для того чтобы определить необходима ли оптимизация по конкретному слову, необходимо определить принадлежит ли сайт к классу сайтов к которому относится это слово.

С помощью коэффициента конкордации можно не просо определить на сколько сайты продвинуты по данному ключевому слову, но и так же на основе уже известных сайтов определить принадлежность неизвестных сайтов к данному классу.

Рассмотрев свойства коэффициента конкордации во второй главе, можно сделать следующие выводы: чем ближе коэффициент конкордации к единице, тем сильнее статистическая связь между исследуемыми объектами. А значит, если при исследовании на статистическую значимость сайтов,  коэффициент конкордации будет понижаться, значит связь между объектами ослабляется и исследуемые сайты трубеют оптимизации.

Для примера, я исследую список сайтов, и проанализирую, принадлежат ли они к финансовому классу сайтов.

Первый шаг, это составление семантического ядра. Ключевыми словами выберу названия котировок ценных бумаг: GAZR; GAZP; GMKN; LKOH; ROSN; SBER; RUB; USD; RTS. Эти слова относятся к финансовым сайтам и их характеризуют, так как они являются уникальными.

Как говорилось ранее, коэффициент конкордации -  это измеритель статистической связи между несколькими (более чем двумя) переменными. В качестве переменных рассмотрим позиции обследуемых объектов в поисковых системах, таких как Yandex.ru; Rambler.ru; Mail.ru; Google.ru; Yahoo.com; Bing.com. Статистически обследованными объектами являются сайты, которые мы проверяем на принадлежность к определенному классу сайтов. Рассмотрим позиции следующих сайтов:  www.rts.ru; www.prime-tass.ru; www.finmarket.ru; www.reuters.com; www.stockportal.ru; www.mfd.ru; www.businessweek.com; www.bfm.ru; www.fincake.ru., и определим существует ли между ними связь. На основе результатов проверю сайт www.rbc.ru, на принадлежность к финансовым сайтам, и определю по каким из ключевых слов надо проводить оптимизацию.

Для каждого из ключевых слов составим таблицу размером mxn.

Где m- число анализируемых порядковых переменных, то есть поисковых систем; n- число статистически обследованных объектов или длина ранжировки, то есть число исследуемых сайтов. Для заполнения этой таблицы используется сервис www.bodrenko.org, значения которые мы на нем получаем это позиции сайтов по данным запросам в соответствующих поисковых системах. (Рис.1)

 

Рис.1

Получаются таблицы следующего вида:

Рис.2

Порядковая переменная позволяет упорядочивать статистически обследованные объекты по степени проявления в них анализируемого свойства. Таким образом, результатом измерения порядковой переменной является приписывание каждому из обследованных объектов некоторой условной числовой метки, обозначающей место этого объекта в ряду из всех n анализируемых объектов, упорядоченном по убыванию степени проявления в них к-го изучаемого свойства.

Итак, в результате измерения порядковых переменных на каждом из анализируемых объектов мы получили таблицу исходных данных следующего вида, который представлен на (рис.2). В этой таблице под элементами х[i][k] задается порядковое место (ранг), которое занимает объект в ряду всех статистически обследованных объектов, упорядоченном по убыванию степени проявления j-го анализируемого свойства красными цифрами. Если рассмотреть столбец с номером j этой таблицы, то он будет представлять перестановку из n элементов, а именно перестановку из n натуральных чисел, определяющую порядковые места объектов (сайтов) в ряду упорядоченном по свойству. При упорядочении объектов могут встречаться ситуации, когда два или более объектов оказываются неразличимыми. Тогда каждому из объектов этой группы приписывается ранг, равный среднему арифметическому значению тех мест, которые они делят, а полученные таким образом ранги принято называть «объединенными».

Рассмотрим каждую из этих таблиц.

 

 

 

 

 

 

 

 

 

 

Таблица для ключевого слова Sber

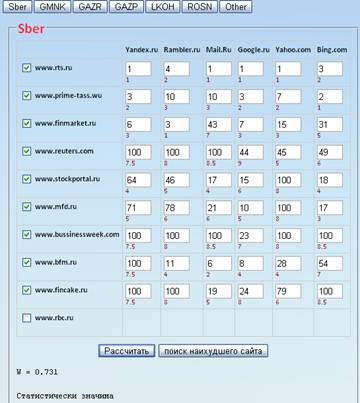
Для ключевого слова Sber, проверим набор заданных сайтов. Вычисляя коэффициент конкордации, получаем:

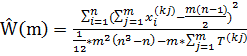 =0,731. Проверим, существует ли связь между анализируемыми переменными. Связаны ли между собой эти сайты. Проверяется это с помощью формулы: m(n-1) Ŵ (m)> χ_α² (n-1)

Значение χ_α² (n-1) берется из таблицы χ² –распределения. Задавшись уровнем значимости критерия α=0,05, находим из таблицы П.4 значение 5% точки χ² –распределения с 9 степенями свободы χ_0,05²=16,91.    Подставляя значения в левую часть неравенства : m(n-1) Ŵ (m)=6*9*0,676=36,504.

Получается что неравенство: m(n-1) Ŵ (m)> χ_α² (n-1) выполнено, а значит, мы можем объявить, что связь между 9 исследуемыми переменными статистически значима. Следовательно, все эти сайты действительно принадлежат к одному и тому же классу. Теперь с полной уверенностью можно на основе этих сайтов и данного ключевого слова проверять сайт www.rbc.ru  на принадлежность к данной группе. Рассчитаем коэффициент еще раз, но включая к сайтам - сайт www.rbc.ru .

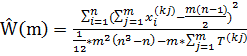 =0,676. Статистическая связь сохранилась, а значит данный сайт относится к финансовым сайтам. Но так как коэффициент понизился, то по данному слову стоит продвигать сайт, а значит изменить структуру сайта, разместить больше ссылок на сайте с этим словом.

 

 

 

 

 

 

 

 

 

 

Рассмотрим ключевое слово GAZR.

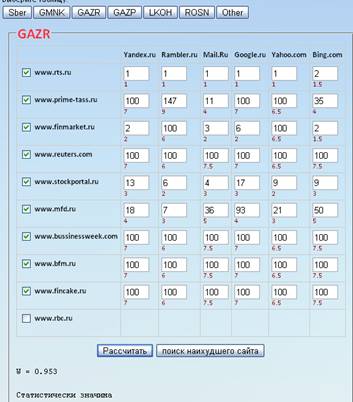
Так же измерим статистическую связь между данной группой сайтов. Вычислим коэффициент согласованности:

.

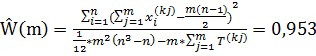Как мы видим, по данному слову набор сайтов достаточно оптимизирован, и практически достигает максимума. Можно сказать, что по ключевому слову GAZR оптимизация не требуется. Проверяем существование связи между анализируемыми переменными по данному слову.

В данную формулу m(n-1) Ŵ (m)> χ_α² (n-1)  подставляем значения,  получаем  m(n-1) Ŵ (m)= 6*9*0,918=49,57

А так как χ_0,05²=16,91, значит неравенство выполнено, а значит и существует связь между переменными, и они принадлежат к одному и тому же классу.

Рассчитаем коэффициент с сайтом www.rbc.ru :

.

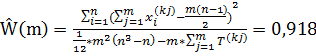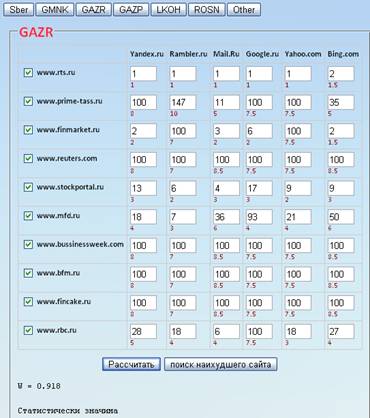
Статистическая значимость сохранилась, коэффициент близок к максимуму, значит сайт финансовый и по данному ключевому слову оптимизация не требуется.

Ключевое слово ROSN.

Вычисляем коэффициент конкордации:

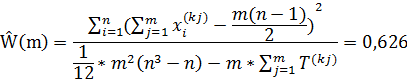
Статистическая связь между переменными по данному слову существует, так как выполняется неравенство: m(n-1) Ŵ (m)> χ_α² (n-1)

Где m(n-1) Ŵ (m)=6*9*0,653=35,26;   χ_0,05² (9) =16,91.

Теперь при данном ключевом слове так же можно проверять сайт www.rbc.ru на принадлежность к финансовой группе сайтов.

Рассчитаем коэффициент согласованности уже для 10 объектов:

 

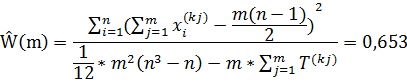
Статистическая значимость сохраняется, а значит можно говорить, что сайт так же является финансовым. И так как коэффициент согласованности повысился, значит, исследуемый сайт улучшил картину по данному ключевому слову во всех поисковых системах.

Ключевое слово GAZP:

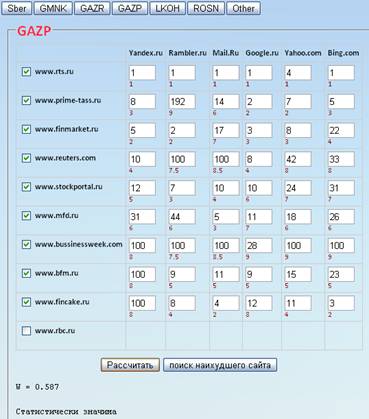
Для ключевого слова GAZP, проверим набор заданных сайтов. Вычисляя коэффициент конкордации, получаем:

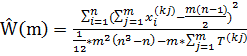 =0,587. Проверим, существует ли связь между анализируемыми переменными. Связаны ли между собой эти сайты. Проверяется это с помощью формулы: m(n-1) Ŵ (m)> χ_α² (n-1)

Значение χ_α² (n-1) берется из таблицы χ² –распределения. Задавшись уровнем значимости критерия α=0,05, находим из таблицы П.4 значение 5% точки χ² –распределения с 9 степенями свободы χ_0,05²=16,91.    Подставляя значения в левую часть неравенства : m(n-1) Ŵ (m)=6*9*0,587=31,698.

Получается что неравенство: m(n-1) Ŵ (m)> χ_α² (n-1) выполнено, а значит, мы можем объявить, что связь между 9 исследуемыми переменными статистически значима. Следовательно, все эти сайты действительно принадлежат к одному и тому же классу. Теперь с полной уверенностью можно на основе этих сайтов и данного ключевого слова проверять сайт www.rbc.ru  на принадлежность к данной группе. Рассчитаем коэффициент еще раз, но включая к сайтам - сайт www.rbc.ru .

 

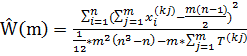 =0,55. Статистическая связь сохранилась, а значит данный сайт относится к финансовым сайтам. Но так как коэффициент понизился, то по данному слову сайт www.rbc.ru требует оптимизации, а значит необходимо изменить структуру сайта, разместить больше ссылок на сайте с этим словом.

 

 

 

 

 

 

Далее ключевое слово GMNK:

Для ключевого слова GMNK, проверим набор заданных сайтов. Вычислим коэффициент конкордации:

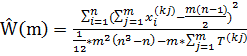 =0,543. Проверим, существует ли связь между анализируемыми переменными. Связаны ли между собой эти сайты. Проверяется это с помощью формулы: m(n-1) Ŵ (m)> χ_α² (n-1)

Значение χ_α² (n-1) берется из таблицы χ² –распределения. Задавшись уровнем значимости критерия α=0,05, находим из таблицы П.4 значение 5% точки χ² –распределения с 9 степенями свободы χ_0,05²=16,91.    Подставляя значения в левую часть неравенства : m(n-1) Ŵ (m)=6*9*0,543=29,322.

Получается что неравенство: m(n-1) Ŵ (m)> χ_α² (n-1) выполнено, а значит, мы можем объявить, что связь между 9 исследуемыми переменными статистически значима. Следовательно, все эти сайты действительно принадлежат к одному и тому же классу. Теперь на основе этих сайтов и данного ключевого слова проверим сайт www.rbc.ru  на принадлежность к финансовым сайтам. Рассчитаем коэффициент еще раз, но включая к сайтам - сайт www.rbc.ru .

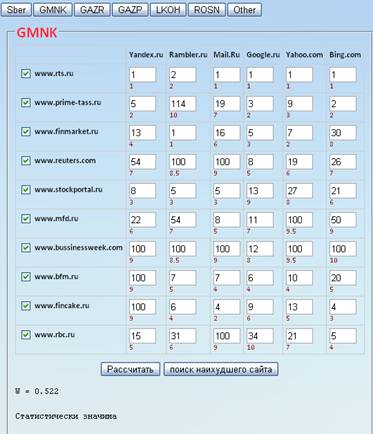
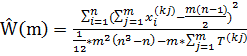 =0,522. Статистическая связь сохранилась, а значит данный сайт относится к финансовым сайтам. Но так как коэффициент понизился, то по данному слову сайт www.rbc.ru требует оптимизации, а значит необходимо изменить структуру сайта, разместить больше ссылок на сайте с этим словом.

 

 

 

 

 

 

 

 

Рассчитаем все тоже самое для ключевого слова LKOH:

Проверим набор заданных сайтов. Вычислим коэффициент конкордации:

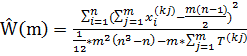 =0,603. Проверим, существует ли связь между анализируемыми переменными. Связаны ли между собой эти сайты. Проверяется это с помощью формулы: m(n-1) Ŵ (m)> χ_α² (n-1)

Значение χ_α² (n-1) берется из таблицы χ² –распределения. Задавшись уровнем значимости критерия α=0,05, находим из таблицы П.4 значение 5% точки χ² –распределения с 9 степенями свободы χ_0,05²=16,91.    Подставляя значения в левую часть неравенства : m(n-1) Ŵ (m)=6*9*0,603=32,562.

Получается что неравенство: m(n-1) Ŵ (m)> χ_α² (n-1) выполнено, а значит, мы можем объявить, что связь между 9 исследуемыми переменными статистически значима. Следовательно, все эти сайты действительно принадлежат к одному и тому же классу. Теперь на основе этих сайтов и данного ключевого слова проверим сайт www.rbc.ru  на принадлежность к финансовым сайтам. Рассчитаем коэффициент еще раз, но включая к сайтам - сайт www.rbc.ru .

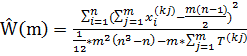 =0,581. Статистическая связь сохранилась, а значит, данный сайт относится к финансовым сайтам. Но так же как и для ключевого слова GMNK коэффициент понизился, следовательно статистическая связь ослабла, и  по данному слову сайт www.rbc.ru требует оптимизации, а значит необходимо изменить структуру сайта, разместить больше ссылок на сайте с этим словом.

 

 

 

 

 

 

 

Вывод

Рассмотрев коэффициент конкордации как измеритель статистической связи между несколькими порядковыми переменными, был проанализирован сайт www.rbc.ru по следующим ключевым словам: GAZR; GAZP; GMKN; LKOH; ROSN; SBER.. Данные слова являются названиями котировок ценных бумаг, которые принадлежат наиболее крупным Российским компаниям.

В результате проведенной работы можно сделать следующие выводы:

Сайт является финансовым, но требует оптимизации по предложенным ключевым словам. В ходе сравнения проверяемого сайта с группой заданных и известных сайтов выяснили, что статистическая связь ослабевает.

По одним из предложенных слов  сайт оптимизирован больше, по одним меньше. По ходу проверки выяснилось, что для ключевого слов  SBER - сайт www.rbc.ru недостаточно оптимизирован, так как самое высокое значение получается при расчете коэффициента согласованности  для заданной группы сайтов, не включая проверяемый сайт. А именно для ключевого слова SBER и набора 9 заданных сайтов коэффициент согласованности  W=0,731;

Для ключевого слова ROSN сайт www.rbc.ru улучшил статистическую связь, так как повысился коэффициент согласованности для данной структуры сайтов.

Предложенный мной алгоритм позволяет проверять любой созданный сайт на принадлежность к финансовым сайтам.

Помимо этого, предлагается универсальный раздел, в котором пользователь может проверять любые сайты с любыми ключевыми словами на принадлежность к определенной группе сайтов.

 

 

 

 

 

 

Создана таблица следующего вида:

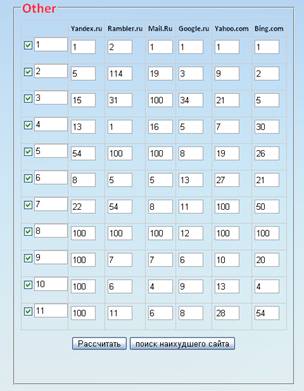
В левом столбце необходимо ввести названия проверяемых сайтов от 1 до 10, относящихся к одной группе. В ячейках  под названиями поисковых систем соответственно вводятся позиции занимаемые сайтами по конкретному ключевому слову. После чего также как было рассмотрено выше, высчитывается коэффициент конкордации по формуле:

 

 

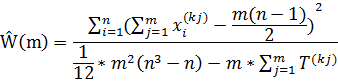
Затем вводится название проверяемого сайта в 11 строке, вместе с позициями, которые он занимает в поисковых системах по ключевому слову. Опять же рассчитывается коэффициент согласованности, и проверяется статистическая связь. Если связь существует, следовательно, проверяемый сайт относится к группе предложенных сайтов.

Под таблицей расположены две кнопки - «рассчитать», «Найти сайт с наибольшим W». С помощью кнопки «Рассчитать », производится расчет коэффициента и проверка на статистическую значимость. Кнопка «Поиск наихудшего сайта» используется, чтобы найти сайт из-за которого, коэффициент согласованности понижается, или пропадает статистическая связь между сайтами.

Инструкция по использованию универсального блока:

1.                Пользователь выбирает сайт, который он хочет проверить.

2.                Выбирается базовый набор сайтов, относящихся к одной определенной группе сайтов. Названия заносятся в первый столбец. Позиции, занимаемые сайтами на поисковых системах по данному ключевому слову, получаем, используя сервис www.bodrenko.org

3.                Проверяется базовый набор сайтов, на статистическую связь. Для этого необходимо нажать «Рассчитать».

4.                Добавляем проверяемый сайт к базовым сайтам, и вычисляем коэффициент согласованности. Если статистическая связь сохранилась, то сайт принадлежит к группе заданных сайтов.

 

 

 

 

 

 

 

 

 

 

 

 

 

Алгоритм программы

Рассматривается 6 порядковых переменных – поисковых систем, и соответствующие им упорядочения девяти объектов.

В соответствии с формулами сначала высчитывается:

S=² , где m=6, n=9;

Далее высчитываются  .

Полученные значения подставляем в формулу 

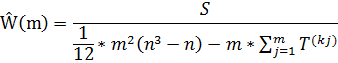
Пользуясь фактом χ² (9)-распределенности случайной величины

m(n-1). Задавшись уровнем значимости критерия α=0,05 рассчитываем значение 5%-ной точки  χ² – распределения с 9 степенями свободы. Для этого необходимо вычислить верхний предел интеграла от функции: f=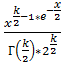 . Находим верхний предел функции, и сравниваем его значение со значением, посчитанным по формуле m(n-1). Если

 m(n-1) Ŵ (m)> χ_α² (n-1) выполнено, то объявляем связь значимой. Если не выполнено – не статистически значимой.

Текст программы приведен в приложении.

 

 

 

 

 

 

 

 

 

Заключение.

В работе были решены задачи:

ü    Рассмотрен коэффициент конкордации (согласованности) как измеритель статистической связи между несколькими порядковыми переменными, где в качестве переменных использовались позиции следующих сайтов: www.rts.ru; www.prime-tass.ru; www.finmarket.ru; www.reuters.com; www.stockportal.ru; www.mfd.ru; www.businessweek.com; www.bfm.ru; www.fincake.ru ., которые они занимают в поисковых системах : Yandex.ru; Rambler.ru; Mail.ru; Google.ru; Yahoo.com; Bing.com с использованием ключевых слов, таких как: GAZR; GAZP; GMKN; LKOH; ROSN; SBER; RUB; USD; RTS.

ü    Проверена принадлежность рассматриваемых сайтов к группе финансовых сайтов;

ü    проанализирован сайт www.rbc.ru, и определено, что он является финансовым.

С помощью разработанного мною алгоритма на известных сайтах можно найти слабые стороны, а новые сайты можно проверить на принадлежность к финансовой группе сайтов.

Разработан универсальный блок, с помощью которого пользователь сам может выбрать ключевое слово, составить набор известных сайтов, относящихся к определенной группе и на основе результатов определять принадлежность нового сайта к данной группе.

 

 

 

 

 

 

 

 

 

Содержание

Введение……………………………………………………………….3

1.Основные понятия и проблемы поисковой оптимизации………..5

2.Коэффициент конкордации как измеритель статистической связи между   несколькими порядковыми переменными………………………………..11

2.1.Проверка статистической значимости выборочного коэффициента конкордации………………………………………………………………..13

2.2.Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей………………………...14

3. Разработка системы анализа поисковой оптимизации………...18

4.Вывод……………………………………………………………....33

5.Алгоритм программы……………………………………………..36

Заключение…………………………………………………………..37

Приложение………………………………………………………….39