«Основы стандартизации, сертификации и метрологии»

Лекция 4

Тема лекции: «Основные термины и определения метрологии»

Разделы лекции:

 

1. Предмет метрологии. Физические свойства и величины.

2. Измерительные шкалы.

3. Системы физических величин и единиц. Международная система единиц (система СИ).

РАЗДЕЛ 1. ПРЕДМЕТ МЕТРОЛОГИИ. ФИЗИЧЕСКИЕ СВОЙСТВА И ВЕЛИЧИНЫ.

 

ПРЕДМЕТ МЕТРОЛОГИИ.

 

ЧТО ТАКОЕ МЕТРОЛОГИЯ?

 

МЕТРОЛОГИЯ – ЭТО НАУКА ОБ ИЗМЕРЕНИЯХ, МЕТОДАХ И СРЕДСТВАХ ОБЕСПЕЧЕНИЯ ИХ ЕДИНСТВА И СПОСОБАХ ДОСТИЖЕНИЯ ТРЕБУЕМОЙ ТОЧНОСТИ.

 

Федеральный закон «Об обеспечении единства измерений» от 26.06.2008 № 102-ФЗ (последняя редакция: в редакции Федерального закона от 13.07.2015 № 233-ФЗ) регулирует отношения, возникающие при выполнении измерений, установлении и соблюдении требований к измерениям, единицам величин, эталонам единиц величин, стандартным образцам, средствам измерений, применении стандартных образцов, средств измерений, методик (методов) измерений, а также при осуществлении деятельности по обеспечению единства измерений, предусмотренной законодательством Российской Федерации об обеспечении единства измерений, в том числе при выполнении работ и оказании услуг по обеспечению единства измерений.

В Федеральном законе «Об обеспечении единства измерений» установлены основные понятия метрологии.

 

Основное понятие метрологии – измерение.

 

ЧТО ПОНИМАЕТСЯ ПОД ИЗМЕРЕНИЕМ В МЕТРОЛОГИИ?

 

ИЗМЕРЕНИЕ - совокупность операций, выполняемых для определения количественного значения величины.

 

В отличие от количественной информации, получаемой теоретическим путём, то есть посредством вычислений и расчётов, такая информация называется измерительной. Во время измерений проявляются некоторые объективные законы природы. Кроме того, при получении измерительной информации должны соблюдаться определённые правила и нормы, устанавливаемые законодательным путём.

 

Всё это составляет предмет НАУКИ ОБ ИЗМЕРЕНИЯХ – МЕТРОЛОГИИ (от др.-греч. μετρον – мера и λογοξ – речь, слово, учение или наука).

 

Базисное положение этой науки определил основоположник отечественной метрологии Д.И.Менделеев в словах: «... наука начинается ... с тех пор, как начинают измерять; точная наука немыслима без меры». Ему же принадлежит и другое важное замечание: «В природе мера и вес суть главные орудия познания».

 

Предметом метрологии является извлечение измерительной информации о свойствах объектов и процессов с заданной точностью и достоверностью.

 

ЧТО ПОНИМАЕТСЯ ПОД ЕДИНСТВОМ ИЗМЕРЕНИЙ?

 

ЕДИНСТВО ИЗМЕРЕНИЙ - состояние измерений, при котором их результаты выражены в допущенных к применению в Российской Федерации единицах величин, а показатели точности измерений не выходят за установленные границы.

 

ЧТО ТАКОЕ СРЕДСТВО ИЗМЕРЕНИЙ?

 

СРЕДСТВО ИЗМЕРЕНИЙ - техническое средство, предназначенное для измерений.

 

ЧТО ТАКОЕ ТИП СРЕДСТВА ИЗМЕРЕНИЙ?

 

ТИП СРЕДСТВ ИЗМЕРЕНИЙ - совокупность средств измерений, предназначенных для измерений одних и тех же величин, выраженных в одних и тех же единицах величин, основанных на одном и том же принципе действия, имеющих одинаковую конструкцию и изготовленных по одной и той же технической документации.

 

ЧТО ПОНИМАЕТСЯ ПОД СРЕДСТВАМИ МЕТРОЛОГИИ?

 

СРЕДСТВА МЕТРОЛОГИИ – это совокупность средств измерений и метрологических стандартов, обеспечивающих их рациональное использование.

 

ЧТО ТАКОЕ МЕТОД ИЗМЕРЕНИЙ?

 

МЕТОДИКА (МЕТОД) ИЗМЕРЕНИЙ - совокупность конкретно описанных операций, выполнение которых обеспечивает получение результатов измерений с установленными показателями точности.

 

КАКИЕ РАЗДЕЛЫ МЕТРОЛОГИИ СУЩЕСТВУЮТ?

 

В зависимости от предмета различают три раздела метрологии:

 

- ТЕОРЕТИЧЕСКАЯ (ФУНДАМЕНТАЛЬНАЯ),

 

- ЗАКОНОДАТЕЛЬНАЯ и

 

- ПРАКТИЧЕСКАЯ (ПРИКЛАДНАЯ) МЕТРОЛОГИЯ.

 

ТЕОРЕТИЧЕСКАЯ (ФУНДАМЕНТАЛЬНАЯ) МЕТРОЛОГИЯ – раздел метрологии, предметом которого является разработка фундаментальных основ метрологии (рисунок 1.).

 

ЗАКОНОДАТЕЛЬНАЯ МЕТРОЛОГИЯ – раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц физических величин, эталонов, методов и средств измерений, направленных на обеспечение единства и необходимой точности измерений в интересах общества.

 

ПРАКТИЧЕСКАЯ (ПРИКЛАДНАЯ) МЕТРОЛОГИЯ – раздел метрологии, предметом которого являются вопросы практического применения разработок теоретической метрологии и положений законодательной метрологии.

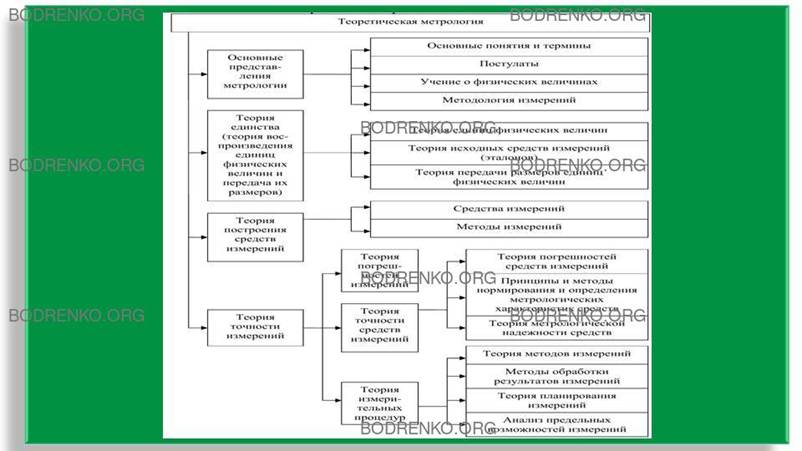
Рисунок 1. Структура теоретической метрологии.

 

ФИЗИЧЕСКИЕ СВОЙСТВА И ВЕЛИЧИНЫ.

 

Все объекты окружающего мира характеризуются своими свойствами.

 

ЧТО ТАКОЕ СВОЙСТВО?

 

СВОЙСТВО – философская категория, выражающая такую сторону объекта (явления, процесса), которая обуславливает его различие или общность с другими объектами (явлениями, процессами) и обнаруживается в его отношениях к ним.

 

Свойство – категория качественная.  Для количественного описания различных свойств процессов и физических тел вводится понятие величины.

 

ЧТО ТАКОЕ ВЕЛИЧИНА?

 

ВЕЛИЧИНА – это свойство чего-либо, которое может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной.

 

КАКИЕ ВИДЫ ВЕЛИЧИН ВЫДЕЛЯЮТ?

 

Анализ величин позволяет разделить их на два вида:

 

- ВЕЛИЧИНЫ МАТЕРИАЛЬНОГО ВИДА (РЕАЛЬНЫЕ) и

 

- ВЕЛИЧИНЫ ИДЕАЛЬНЫХ МОДЕЛЕЙ РЕАЛЬНОСТИ (ИДЕАЛЬНЫЕ), которые относятся главным образом к математике и являются обобщением (моделью) конкретных реальных понятий.

 

КАК РАЗДЕЛЯЮТСЯ РЕАЛЬНЫЕ ВЕЛИЧИНЫ?

 

Реальные величины, в свою очередь, делятся на

 

- ФИЗИЧЕСКИЕ и

 

- НЕФИЗИЧЕСКИЕ.

 

КАК ОПРЕДЕЛЯЕТСЯ ФИЗИЧЕСКАЯ ВЕЛИЧИНА?

 

Физическая величина в самом общем случае может быть определена как величина, свойственная материальным объектам (процессам, явлениям), изучаемым в естественных (физика, химия) и технических науках.

 

КАКИЕ ВЕЛИЧИНЫ ОТНОСЯТСЯ К НЕФИЗИЧЕСКИМ ВЕЛИЧИНАМ?

 

К нефизическим величинам следует отнести величины, присущие общественным (нефизическим) наукам – философии, социологии, экономике и т.п.

 

Объектами измерений являются физические величины (ФВ).

 

Физическая величина - одно из свойств физического объекта, общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них. Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого. Так, все тела обладают массой и температурой, но у каждого из них они различны в количественном отношении.

 

КАЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА ИЗМЕРЯЕМЫХ ВЕЛИЧИН.

 

Формализованным отражением качественного различия между измеряемыми физическими величинами служит их размерность. Размерность обозначается символом dim, происходящим от слова dimension.

 

ЧТО ТАКОЕ РАЗМЕРНОСТЬ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

РАЗМЕРНОСТЬ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ dim Q – выражение в форме степенного многочлена, составленного из произведений символов основных физических величин в различных степенях и отражающее связь данной ФВ с ФВ, принятыми в данной системе за основные с коэффициентом пропорциональности, равным 1:

 

dim Q=L^α·M^β·T^γ·I^η·K,

 

где L, M, T, I ... – размерности соответствующих основных ФВ;

 

α, β, γ, η ... – показатели размерности.

Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулём.

 

Если все показатели размерности равны нулю, то такую величину называют БЕЗРАЗМЕРНОЙ. Она может быть относительной, определяемой как отношение одноимённых величин (например, относительная диэлектрическая проницаемость), или логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений).

 

КАКИМИ ПРАВИЛАМИ РУКОВОДСТВУЮТСЯ ПРИ ОПРЕДЕЛЕНИИ РАЗМЕРНОСТИ?

 

При определении размерности производных ФВ руководствуются следующими правилами:

 

1. Размерности левой и правой частей уравнения равны между собой.

 

2. Алгебра размерностей мультипликативна.

 

3. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между величинами имеет вид

 

Q=A·B·C,

 

то

 

dim Q=dim A·dim B·dim C.

 

4. Размерность частного при делении одной величины на другую равна отношению их размерностей, то есть если

 

Q=A/B, то

 

dim Q=dim A/dim B.

 

5. Размерность любой величины, возведенной в степень, равна её размерности в той же степени. Так, если

 

Q=Aⁿ, то

 

dim Q=(dim A)ⁿ .

Размерность является качественной характеристикой измеряемой величины. Она отражает её связь с основными ФВ и зависит от выбора последних. Как указывал М. Планк, вопрос об истинной размерности любой величины «имеет не более смысла, чем вопрос об истинном названии какого-нибудь предмета». По этой причине во многих гуманитарных науках, где номенклатура и связь основных и производных измеряемых величин ещё не определены, теория размерностей не находит пока эффективного применения. В физике, напротив, методами теории размерностей удается получать важные самостоятельные результаты. Применение анализа симметрий размерностей физических величин позволяет иногда определить неизвестную зависимость между ФВ.

 

КОЛИЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА ИЗМЕРЯЕМЫХ ВЕЛИЧИН.

 

Для того чтобы можно было установить для каждого объекта различия в количественном содержании свойства, отображаемого физической величиной, в метрологии введены понятия ее размера и значения. Количественной характеристикой любого свойства служит размер.

 

ЧТО ТАКОЕ РАЗМЕР ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

РАЗМЕР ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ – это ее количественная определенность, присущая конкретному материальному объекту, системе, явлению или процессу. Например, каждое тело обладает определенной массой, вследствие чего тела можно различать по их массе, то есть по размеру интересующей нас ФВ.

 

Размер является объективной количественной характеристикой, не зависящей от выбора единиц измерений.

 

Например, 1000 мг; 1 г; 0,001 кг – три варианта представления одного и того же размера. Каждый из них является значением физической величины (в данном случае – массы) – выражением размера в тех или иных единицах измерений.

 

ЧТО ТАКОЕ ЗНАЧЕНИЕ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

ЗНАЧЕНИЕ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ – это выражение размера физической величины в виде некоторого числа принятых для нее единиц.

 

КАК ЗАПИСЫВАЕТСЯ ОСНОВНОЕ УРАВНЕНИЕ ИЗМЕРЕНИЯ?

 

Значение физической величины Q можно представить в виде произведения:

 

Q=q·[Q],      (*)

 

где q – отвлечённое число, называемое числовым значением,

 

[Q] – размер единицы измерения данной ФВ.

Значение ФВ находится путем измерения или вычисления в соответствии с основным уравнением измерения (*).

 

Из приведённых примеров видно, что значение, как и размер, от выбора единиц не зависит, в отличие от числового значения. Для одного и того же размера числовое значение тем меньше, чем больше единица измерения (и наоборот), так что произведение в правой части основного уравнения измерения (*) остается постоянным.

 

ЧТО ТАКОЕ ЕДИНИЦА ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

ЕДИНИЦА ВЕЛИЧИНЫ - фиксированное значение величины, которое принято за единицу данной величины и применяется для количественного выражения однородных с ней величин.

 

ЕДИНИЦА ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ – это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице. Она применяется для количественного выражения однородных ФВ.

 

ЧТО ТАКОЕ РАЗМЕР ЕДИНИЦЫ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

РАЗМЕР ЕДИНИЦЫ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ – количественная определенность единицы физической величины, воспроизводимой или хранимой средством измерений.

 

Не следует для выражения количественных соотношений применять словосочетания типа «величина массы», «величина длины», т.к. масса и длина сами являются величинами. Не принято говорить «размер массы (длины, силы, ...)», «значение массы (длины, силы, ...)», говорят просто «масса (длина, сила, ...)».

 

Из-за зависимости числовых значений от размеров единиц ФВ, роль последних очень велика. Если допустить произвол в выборе единиц, то результаты измерений будут несопоставимы между собой, то есть нарушится единство измерений. Чтобы этого не произошло, единицы измерений устанавливаются по определённым правилам и закрепляются законодательным путём. Наличие законодательной метрологии отличает метрологию от других естественных наук (физики, химии и др.) и направлено на обеспечение единства измерений.

 

РАЗДЕЛ 2. ИЗМЕРИТЕЛЬНЫЕ ШКАЛЫ.

 

СПОСОБЫ ПОЛУЧЕНИЯ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ.

 

ЧТО ПРЕДСТАВЛЯЕТ СОБОЙ ИЗМЕРЕНИЕ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

ИЗМЕРЕНИЕ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ – это совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.

 

В этом определении учтена техническая сторона (совокупность операций), раскрыта метрологическая суть измерений (сравнение с единицей) и показан гносеологический аспект (получение значения величины). В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая и не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам.

 

ЧТО ТАКОЕ ПРЯМОЕ ИЗМЕРЕНИЕ?

 

ПРЯМОЕ ИЗМЕРЕНИЕ - измерение, при котором искомое значение величины получают непосредственно от средства измерений.

 

Суть измерения заключается в сравнении. Не существует иного способа получения информации о размере ФВ, кроме как путем сравнения его с другим размером такой же физической величины, то есть имеющей такую же размерность. Измерение суть сравнение размеров опытным путем. Сравнение размеров опытным путем является единственным способом получения измерительной информации. При этом не уточняется, каким образом происходит сравнение размеров одноименных физических величин, с помощью каких приспособлений или даже может быть без них. Просто утверждается, что другого способа нет.

 

КАКИЕ СУЩЕСТВУЮТ ВАРИАНТЫ СРАВНЕНИЯ МЕЖДУ СОБОЙ ДВУХ РАЗМЕРОВ?

 

Вариантов сравнения между собой двух размеров Q_i и Q_j всего три:

 

ВАРИАНТ 1)  Q_i>Q_j, Q_i<Q_j, Q_i= Q_j.       (1)

 

ВАРИАНТ 2) Q_i−Q_j=∆Q_ij.                      (2)

 

ВАРИАНТ 3) Q_i/Q_j=x_ij.                          (3)

Первый вариант самый простой. Экспериментальное решение неравенства (1) позволяет ответить на вопрос: какой из двух размеров больше другого (либо они равны), но ничего не говорит о том, на сколько больше, или во сколько раз. Это наименее информативное измерение. Однако более полная измерительная информация иногда даже не требуется.  В некоторых случаях этого вполне достаточно.

 

Более информативно сравнение по правилу (2). Оно позволяет получить ответ на вопрос о том, на сколько один размер больше или меньше другого (в частном случае они могут оказаться равными). А вот сказать, во сколько раз больше, по-прежнему будет нельзя.

 

Для того, чтобы ответить на вопрос, во сколько раз один размер больше или меньше другого (в частном случае они могут оказаться и равными), нужно сравнить размеры между собой по правилу (3), то есть посмотреть, сколько раз j-й размер укладывается в i-м. Это будет означать, что j-й размер выступает в качестве единицы измерения, а к единицам измерений предъявляются совершенно определённые требования. В частности, для обеспечения единства измерений они должны быть установлены по определённым правилам и закреплены законодательным путём. Следовательно, измерение по правилу (3) представляет собой сравнение неизвестного размера Q_i=Q с узаконенной единицей измерения Q_j=[Q], с целью определения числового значения q измеряемой физической величины, которое показывает, во сколько раз неизвестный размер больше размера единицы, или на сколько единиц он больше нуля. Таким образом, последняя разновидность способа сравнения является самой информативной. Она позволяет определить значение измеряемой физической величины Q, то есть выразить её размер в общепринятых (узаконенных) единицах в кратном или дольном отношении, и отвечает на вопрос, во сколько раз или на сколько (единиц) один размер больше (меньше) другого.

 

Измерение – познавательный процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения. В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства проявляются только качественно, другие – количественно. Многообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой физической величины.

 

ЧТО ПРЕДСТАВЛЯЕТ СОБОЙ ШКАЛА ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

Шкала физической величины представляет собой упорядоченную совокупность значений этой величины, принятую по соглашению на основании результатов точных измерений.

 

Согласно теории измерений измерение трактуется как отображение элементов эмпирической системе с отношениями (совокупность объектов, их свойств и отношений) на элементы абстрактной системы с отношениями (совокупность оценок и правил их образования), осуществляемое по определенной системе правил соотнесения эмпирической и абстрактной систем (совокупность правил и процедур оценивания).

 

Совокупность правил, позволяющих выполнить такое сопоставление эмпирической системы отношений в числовую систему отношений, называется шкалой.

 

КАКИЕ ТИПЫ ШКАЛ ИЗМЕРЕНИЙ РАЗЛИЧАЮТ В ТЕОРИИ ИЗМЕРЕНИЙ?

 

В соответствии с логической структурой проявления свойств в теории измерений различают пять основных типов шкал измерений: две – неметрические шкалы (шкала наименований и шкала порядка) и три – метрические шкалы (шкала интервалов, отношений и абсолютные шкалы).

 

НЕМЕТРИЧЕСКИЕ ШКАЛЫ.

 

1. ШКАЛА НАИМЕНОВАНИЙ (ШКАЛА КЛАССИФИКАЦИИ). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами физических величин. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Условные номера в качестве имен присваиваются по следующему правилу: нельзя присваивать одно имя (число) двум разным объектам. Поскольку числа характеризуются только отношениями эквивалентности, то в них отсутствует понятие нуля, «больше» или «меньше» и единицы измерения.

 

НОМИНАЛЬНОЕ ИЗМЕРЕНИЕ является качественным измерением. Единственный факт, существенный при номинальных измерениях, заключается в том, что одинаковым характеристикам, состояниям и явлениям присваиваются одни и те же метки, а различным характеристикам – разные. Сущностью такого измерения является безусловный смысл равенства и неравенства. Процедура присвоения ограничена лишь тем, что одно имя можно присвоить лишь одному объекту (классу).

 

Примером номинального измерения в технических науках служит целый класс измерений, осуществляемых системами обнаружения. Эти системы конструируются так, чтобы результат их действия был двоичным. Системы пожарной сигнализации вырабатывают сигнал «пожара нет», когда температура ниже определенного значения, и сигнал «пожар», когда температура превышает это значение. В этом случае отношение в эмпирической системе для номинального измерения – тождество. Номинальное измерение не может указать, какое из событий или явлений больше или меньше. Все, что можно определить, это «случилось» или «не случилось». Если число возможных исходов больше двух, то номинальное измерение может указать, какое именно событие произошло. Например, цвет любой вещи можно определить по названию подходящего цвета в атласе цветов, предназначенном для идентификации цвета. Кроме того, с помощью номинального измерения осуществляют классификацию, которая существует во многих разновидностях: например, с помощью диагностических средств классифицируют болезнь, также классифицируют флору, фауну, проводят контроль изделий (классификация на годные и бракованные), осуществляют сложную процедуру распознавания образов и т.д. Номинальная шкала, используемая для классификации, называется шкалой классификации. При классификации существенно лишь то, что единственное отношение в системе объектов, передаваемое шкалой классификации, – это отношение эквивалентности. Так, все годные изделия эквивалентны в том смысле, что могут быть использованы.

 

2. ШКАЛА ПОРЯДКА (ШКАЛА РАНГОВ). Результат экспериментального решения неравенства (1) может быть представлен на шкале порядка, являющейся упорядоченной последовательностью опорных (реперных) точек, обозначаемых буквами, цифрами или символами и соответствующих размерам

 

Q₁<Q₂<Q₃<Q₄<…<Q_n,

 

о каждом из которых известно, что он больше предыдущего, но меньше последующего, хотя сами размеры неизвестны (рисунок 2). Шкала является монотонно изменяющейся и позволяет установить отношение «больше – меньше» между величинами, характеризующими это свойство. Если для обозначения реперных точек используются цифры, то они называются баллами. Обозначения нельзя ни складывать, ни вычитать, ни делить, ни перемножать. На шкале порядка не определены никакие математические операции. В то же время, если один размер по шкале порядка меньше другого, а последний в свою очередь меньше третьего, то и первый размер меньше третьего.

 

То есть для любых чисел a, b и c таких, что a<b и b<c, справедливо соотношение a<c (транзитивность). Эти свойства транзитивности означают, что на шкалах порядка определены (т.е. могут выполняться) логические операции.

Рисунок 2. Построение шкалы порядка.

 

Так как размеры, которым соответствуют реперные точки, неизвестны, то бессмысленно говорить о масштабе на шкале порядка. По шкалам порядка не только нельзя определить, чему равен измеряемый размер Qi , но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Qj. В шкалах порядка принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности. Хотя нуль может и существовать. Тем не менее, в областях, где к измерительной информации не предъявляются высокие требования, шкалы порядка применяются довольно широко. В промышленности, например, для измерений по шкалам порядка используются шаблоны. В образовательных учреждениях по шкале порядка измеряются знания учащихся (таблица 1.):

 

Таблица 1. Шкала оценок знаний учащихся.

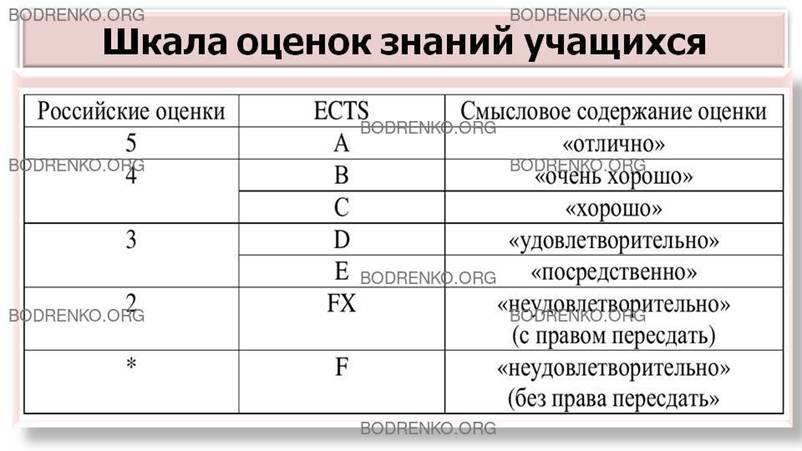
При одномерной шкале порядок должен быть линейным: все объекты должны поддаваться выстраиванию в цепочку по какому-либо признаку (некоторые из них могут занять одно и то же место в цепочке – быть эквивалентными). Так, студенты после экзамена разбиваются на классы получивших оценки 2, 3, 4 и 5 в порядке роста их знаний, но для экзаменатора и внутри этих классов есть различия. Здесь существенно, что более знающему студенту присваивается большее число, и переставлять эти числа уже нельзя. Правда, можно договориться о другом порядке оценок, но это изменит всю систему. Так, суждения о студентах не изменились бы, если бы вместо оценок 2, 3, 4 и 5 ставились 5, 10, 20 и 35 (мог бы измениться средний балл, но это потому, что средний балл является так называемой неадекватной статистикой для шкалы порядка).

 

Группа допустимых преобразований для шкалы порядка должна уничтожать пропорциональность (ведь знания, оцененные на 4, нельзя считать вдвое более обширными или глубокими, чем знания, оцененные на 2) и отношение «быть суммой» (получить 2 и 3 – не то же, что получить 5), сохраняя лишь отношения большего и меньшего.

 

Итак, порядковое измерение занимает нижнюю ступень в количественных измерениях. Упорядочение в шкале порядка может осуществляться по внешним признакам – нумерация – или по внутренним свойствам – ранжирование. Пример первой процедуры – нумерация мест в театре, домов, исследуемых образцов, промышленных изделий и т.д. Примеры второй процедуры – ранжирование силы ветра (волнения) на море (12-балльная шкала Бофорта для силы морского ветра) (таблица 2), ранжирование силы землетрясений (шкала Рихтера), шкала вязкости Энглера, ранжирование твердости минералов (шкала Мооса).

 

Таблица 2. Шкала Бофорта для измерения силы ветра.

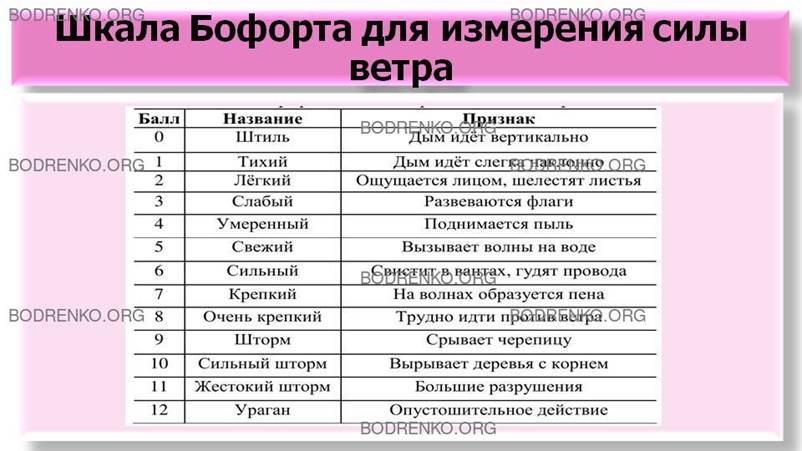
Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам относится шкала Мооса для определения твердости минералов (таблица 3.). В ней определенным стандартным минералам от талька до алмаза в порядке возрастания их твердости присвоены целые числа от 1 до 10.

 

Таблица 3. Минералогическая шкала твёрдости.

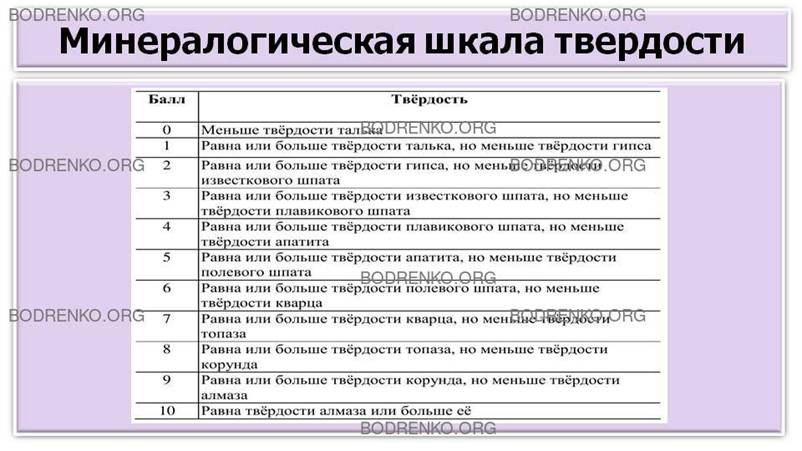
Определение значений величин с помощью шкал порядка нельзя считать измерениями, так как на них отсутствуют единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным.

 

МЕТРИЧЕСКИЕ ШКАЛЫ.

 

3. ШКАЛА ИНТЕРВАЛОВ (ШКАЛА РАЗНОСТЕЙ). Данные шкалы являются дальнейшим развитием шкал порядка и относятся уже к метрическим шкалам. Шкала состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. На шкалах интервалов по сравнению с неметрическими шкалами установлен масштаб.

 

Шкала интервалов представляет собой результат экспериментального сравнения i-го размера с j-м, проведенный по правилу (2). Пример построения шкалы интервалов приведён на рисунке 4., где в качестве j-го размера выбран третий. Если бы для сравнения были выбраны четвертый или пятый размеры, то нуль сместился бы выше по шкале интервалов; если бы второй или первый – ниже.

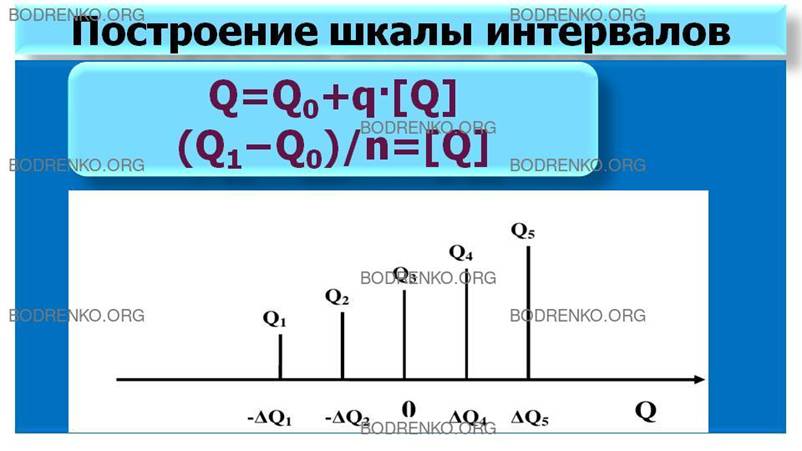
Рисунок 3. Построение шкалы интервалов.

 

Таким образом, начало отсчёта на шкале интервалов не определено и зависит от выбора размера, с которым производится сравнение. Для обеспечения единства измерений этот размер должен быть общепринятым или установленным законодательно.

 

Шкала интервалов величины Q описывается уравнением

 

Q=Q₀+q·[Q] ,

 

где q – числовое значение величины;

 

Q₀ – начало отсчета шкалы:

 

[Q] – единица данной величины.

 

Такая шкала полностью определяется заданием начала отсчета Q₀ и единицы данной величины [Q]. Выбираются два размера Q₀ и Q₁ величины, которые относительно просто реализованы физически в наиболее чистом виде. Эти размеры называются опорными точками, или основными реперами, а интервал (Q₁−Q₀) – основным интервалом. Точка Q₀ принимается за начало отсчета, а величина

 

(Q₁−Q₀)/n=[Q]

 

за единицу Q.  При этом n выбирается таким, чтобы [Q] было целой величиной.

 

Перевод одной шкалы интервалов

 

Q=Q₀₁+q₁·[Q]₁

 

в другую

 

Q=Q₀₂+ q₂·[Q]₂

 

проводится по формуле:

К шкалам интервалов относится летоисчисление по различным календарям.

 

Температурные шкалы также являются шкалами интервалов. Так, например, по температурным шкалам Цельсия и Реомюра первая опорная точка или начало отсчета – температура таяния льда, по шкале Фаренгейта – температура смеси льда с солью и нашатырём, по шкале Кельвина – температура, при которой прекращается тепловое движение молекул (рисунок 4). Второй опорной точкой на трёх температурных шкалах (Цельсия, Реомюра, Фаренгейта) является температура кипения воды при номинальном значении атмосферного давления.

Рисунок 4. Температурные шкалы Цельсия (°С), Кельвина (°К), Фаренгейта (°F) и Реомюра (°R)

 

На шкале Цельсия интервал между опорными точками разбит на 100 градаций – градусов; на шкале Реомюра – на 80; на шкале Фаренгейта – на 180. При этом на шкале Фаренгейта, по сравнению с предыдущими шкалами, начало отсчёта сдвинуто на 32°F в сторону низких температур (то есть на шкале Фаренгейта температура тающего льда соответствует +32°F, а температура кипящей воды составляет +212°F, температура человеческого тела +96°F). Таким образом, единицы измерения температуры в шкале Цельсия и Фаренгейта различаются. Градус Фаренгейта в 1,8 раза меньше градуса Цельсия. Шкалой Фаренгейта до настоящего времени пользуются в США. Пересчет значения температуры из одной шкалы в другую осуществляется по формуле:

 

t°C=5/9(h°F−32),

 

h°F=9/5(t°C +32).

 

На шкале Кельвина в качестве второй опорной точки выбрана температура таяния льда, а интервал между реперными точками разбит на 273,16 частей с тем, чтобы одна такая часть, называемая Кельвином, в точности равнялась 1°С (1°C=1°K). Это значительно упрощает переход от одной шкалы к другой.

 

Градации являются единицами измерений интервалов между размерами, но не самих размеров физических величин. В качестве градаций могут использоваться и узаконенные единицы измерений физических величин. Выражение интервала в тех или иных единицах измерений называется его значением. Интервалы можно сравнивать между собой двумя способами, во-первых, по принципу, на сколько один интервал больше или меньше другого, во-вторых, по принципу – во сколько раз. Что же касается размеров физических величин, то по шкале порядка можно получить только информацию о том, на сколько один размер больше или меньше другого. Если, например, второй размер больше первого на семь градаций, а третий меньше второго на две, то первый меньше третьего на пять градаций. На шкале интервалов определены только аддитивные математические операции. Получить информацию о том, во сколько раз один размер больше другого, по шкале интервалов невозможно. Для этого нужно знать сами размеры, сведений о которых на шкале интервалов нет.

 

4. ШКАЛА ОТНОШЕНИЙ. Шкала отношений служит для представления результатов измерений, полученных посредством экспериментального сравнения i-го размера с j-м по правилу (3). В этих шкалах существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения эта шкала является шкалой интервалов с естественным началом отсчета. К значениям, полученным по шкале отношений, применимы все арифметические действия, что имеет важное значение при измерении физических величин. Шкалы отношений являются самыми совершенными. Они описываются уравнением

 

Q=q·[Q] ,

 

где Q – физическая величина, для которой строится шкала,

 

[Q] – ее единица измерения,

 

q – числовое значение физической величины.

 

Шкалы отношений являются самыми совершенными, самыми информативными и самыми распространёнными. На них представлена информация о самих размерах физических величин, в частности – об их значениях. Это позволяет решать и на сколько, и во сколько раз один размер больше или меньше другого. На шкалах отношений определены любые математические операции.

 

Переход от одной шкалы отношений к другой происходит в соответствии с уравнением:

 

q₂=(q₁·[Q]₁)/[Q]₂.

 

 

5. АБСОЛЮТНЫЕ ШКАЛЫ. Процесс ужесточения (усиления) шкал приводит к понятию абсолютной шкалы, которая устанавливает однозначное (единственно возможное) соответствие между объектами и числами. Иначе говоря, абсолютные шкалы обладают всеми признаками шкал отношений, но дополнительно имеют естественное однозначное определение единицы измерения и соответственно не зависят от принятой системы единиц измерения.

 

Абсолютная шкала может использоваться для измерения относительных величин. Действительно, такие величины, как коэффициент усиления или затухания, коэффициент трения, коэффициент полезного действия, добротность колебательной системы, вероятность, относительная частота появления события в серии испытаний и т. п., выражаются отвлеченными числами, не зависящими от выбора единиц, а при измерении этих величин не требуется эталонов. Свойствами относительных величин обладают также геометрические и фазовые углы. Относительные величины могут выражаться в безразмерных единицах (когда отношение двух одноименных величин равно 1), в процентах % (когда отношение равно 10⁻²), промилле % ₀ (отношение равно 10⁻³) или в миллионных долях ppm (отношение равно 10⁻⁶).

 

Особый интерес представляет группа величин с ограниченными шкалами (такие, как коэффициент полезного действия, вероятность). Их значения могут находиться только в пределах от 0 до 1, причем конечные точки этого диапазона физически как бы бесконечно удалены, недостижимы (на практике это обстоятельство вынуждает перейти к логарифмическим оценкам вблизи этих точек).

 

Логарифмическая величина представляет собой логарифм безразмерного отношения двух одноименных физических величин. Логарифмические величины применяют для выражения уровня звукового давления, усиления, ослабления, выражения частотного интервала и т.д.

 

Единицей логарифмической величины является бел (Б), определяемый соотношением

 

1Б=lg (P₂/P₁)

 

при P₂=10·P₁,

 

где P₁ и P₂ – одноименные энергетические величины мощности, энергии, плотности энергии и т.д.

 

В случае, если берется логарифмическая величина для отношения двух «силовых» величин (напряжения, силы тока, давления, напряженности поля и т.п.), бел определяется по формуле

 

1Б=2lg(F₂/F₁)

 

при F₂=√10·F₁.

 

Дольной единицей от бела является децибел, равный 0,1 Б.

РАЗДЕЛ 3. СИСТЕМЫ ФИЗИЧЕСКИХ ВЕЛИЧИН И ЕДИНИЦ. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИСТЕМА СИ).

 

По степени условной независимости от других величин данной группы ФВ делятся на  основные (условно независимые),  производные (условно зависимые) и  дополнительные.

 

ОСНОВНЫЕ ВЕЛИЧИНЫ выбираются обосновано, но в общем произвольным образом.

 

ПРОИЗВОДНЫЕ ВЕЛИЧИНЫ выражаются через основные на основе известных уравнений связи между ними.

 

ЧТО ТАКОЕ СИСТЕМА ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН?

 

Совокупность основных и производных единиц ФВ, образованная в соответствии с принятыми принципами, называется системой единиц ФВ.

 

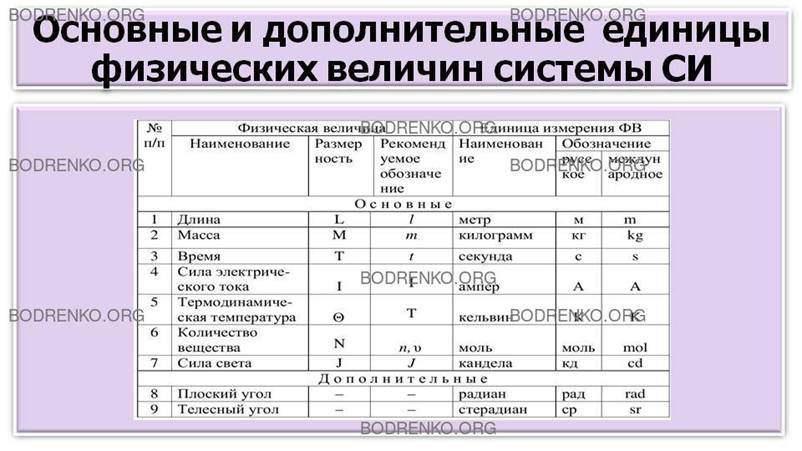
Единица основной ФВ в данной системе является основной единицей системы. Действующая в настоящее время «Международная система единиц» (сокращенное обозначение система СИ (SI) «система интернациональная») была принята ХI Генеральной конференцией по мерам и весам в 1960 году. Система СИ состоит из 7 основных, 2 дополнительных и ряда производных единиц. Наименования основных и дополнительных единиц ФВ приведены в таблице 4.

 

Система СИ возникла не на пустом месте и является логическим развитием предшествовавших ей систем единиц:

 

СГС (основные единицы: сантиметр – грамм – секунда),

 

МКГСС (основные единицы: метр – килограмм-сила – секунда),

 

МКС (основные единицы: метр – килограмм – секунда) и др.

 

Таблица 4. Основные и дополнительные единицы ФВ системы СИ.

В названии системы ФВ применяют символы величин, принятых за основные. Например, система величин механики, в которой в качестве основных используются длина (L), масса (М) и время (Т), называется системой LMT. Действующая международная система единиц СИ должна обозначаться символами LMTIΘNJ, обозначающими соответственно символы основных величин: длины (L), массы (М) и времени (Т), силы электрического тока (I), температуры (Θ), количества вещества (N) и силы света (J).

 

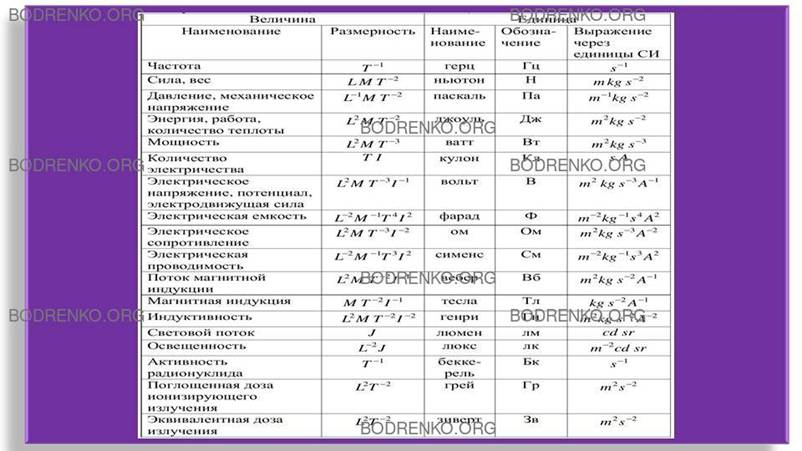
Производная единица системы единиц – это единица производной ФВ системы единиц, образованная в соответствии с уравнением, связывающим ее с основными единицами или же с основными и уже определенными производными единицами. Производные единицы системы СИ, имеющие специальное название, приведены в таблице 5.

 

Таблица 5. Производные единицы системы СИ, имеющие специальное название.

Производные единицы бывают когерентными и некогерентными.

 

ЧТО ТАКОЕ КОГЕРЕНТНАЯ ПРОИЗВОДНАЯ ЕДИНИЦА ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

КОГЕРЕНТНОЙ называется производная единица ФВ, связанная с другими единицами системы уравнением, в котором числовой коэффициент принят равным 1.

 

Различают кратные и дольные единицы ФВ.

 

КРАТНАЯ ЕДИНИЦА – это единица ФВ, в целое число раз большая системной или внесистемной единицы.

 

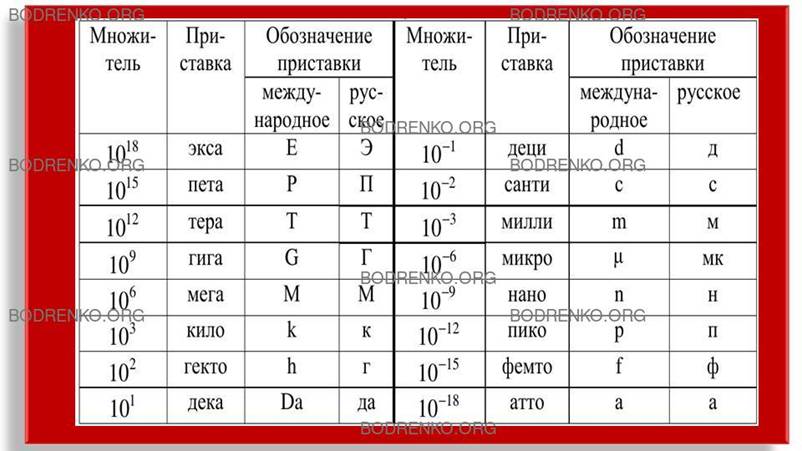
ДОЛЬНАЯ ЕДИНИЦА – единица ФВ, в целое число раз меньшая системной или внесистемной единицы. Приставки для образования кратных и дольных единиц СИ приведены в таблице 6.

 

Таблица 6.  Множители и приставки для образования десятичных кратных и дольных единиц и их наименований.

Единицы ФВ делятся на системные и внесистемные.

 

ЧТО ТАКОЕ ВНЕСИСТЕМНАЯ ЕДИНИЦА ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

ВНЕСИСТЕМНАЯ ЕДИНИЦА – это единица ФВ, не входящая ни в одну из принятых систем единиц.

 

 НА КАКИЕ ВИДЫ РАЗДЕЛЯЮТСЯ ВНЕСИСТЕМНЫЕ ЕДИНИЦЫ?

 

Внесистемные единицы разделяют на четыре вида:

 

1. Допускаемые наравне с единицами СИ, например: единица массы – тонна; единицы плоского угла – градус, минута, секунда; единица объема – литр и др. Внесистемные единицы, допускаемые к применению наравне с единицами СИ, приведены в таблице 7.

 

2. Допускаемые к применению в специальных областях, к которым относятся: единицы длины (в астрономии) – астрономическая единица, парсек, световой год; единица оптической силы (в оптике) – диоптрия; единица энергии (в физике) – электрон-вольт, приведены в таблице 4.

 

3. Временно допускаемые к применению наравне с единицами СИ, например: в морской навигации – морская миля; в ювелирном деле единица массы – карат и др. Эти единицы должны изыматься из употребления в соответствии с международными соглашениями.

 

4. Изъятые из употребления, к ним относятся единицы давления – миллиметр ртутного столба; единица мощности – лошадиная сила и др., приведены в таблице 8.

 

Таблица 7. Внесистемные единицы, допускаемые к применению наравне с единицами СИ.

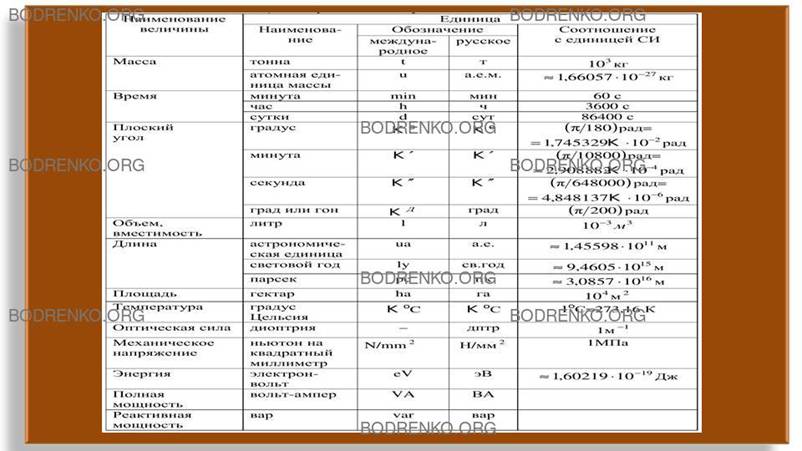
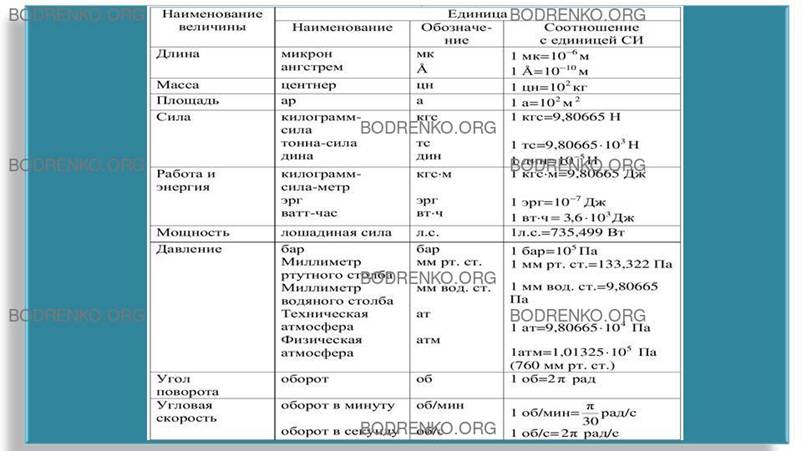
Таблица 8. Внесистемные единицы, изъятые из употребления, и их связь с единицами системы СИ.

ЧТО ТАКОЕ СИСТЕМНАЯ ЕДИНИЦА ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ?

 

СИСТЕМНАЯ ЕДИНИЦА – единица ФВ, входящая в одну из принятых систем. Все основные, производные, кратные и дольные единицы являются системными.

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Герасимова Е.Б., Герасимов Б.И. Метрология, стандартизация и сертификация: Учебное пособие – 2-е изд.-  М.: ФОРУМ: НИЦ ИНФРА-М, 2015. – 224 с.

 

[2] Кошевая И. П., Канке А. А. Метрология, стандартизация, сертификация: Учебник — М.: ИД «ФОРУМ»: ИНФРА-М, 2013. - 416 с.

[3] Крылова Г.Д. Основы стандартизации, сертификации, метрологии: Учебник для вузов.  – М.: ЮНИТИ-ДАНА, 2015. – 671 с.

 

[4] Лифиц И. М. Стандартизация, метрология и подтверждение соответствия: Учебник для бакалавров. — М.: Юрайт: ИД «ЮРАЙТ», 2013. — 411 с.

 

[5] Сергеев А. Г., Терегеря В.В. Метрология, стандартизация и сертификация: Учебник для бакалавров.  — М.: Юрайт: ИД Юрайт, 2013. — 838 с.