Контрольные вопросы

к лекции № 3 «Приемы разработки и выбора управленческих решений в условиях риска и неопределенности»

по предмету

«Методы принятия управленческих решений»

 

1.      Матричная игра задана платежной матрицей A. Найти чистую нижнюю цену игры.

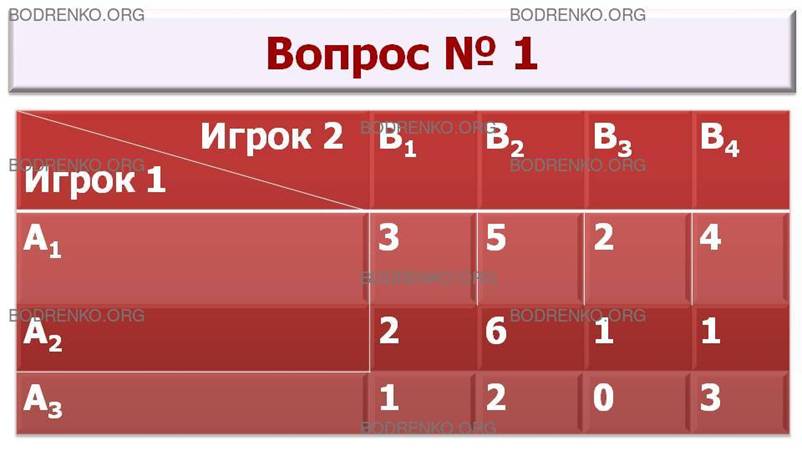
  A =

3	5	2	4
2	6	1	1
1	2	0	3

 

 

 

 

 

A)  4;

      Б)  2;

      В)  1.

 

2.      Матричная игра задана платежной матрицей A. Найти чистую верхнюю цену игры.

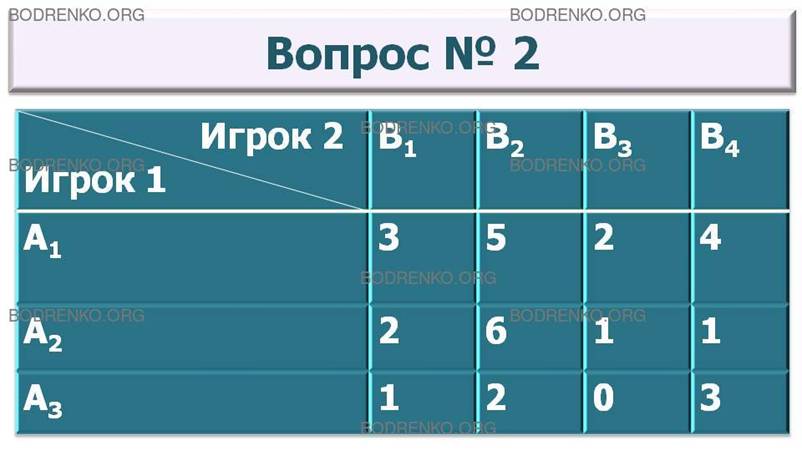
  A =

3	5	2	4
2	6	1	1
1	2	0	3

 

 

 

 

 

 

A)   2;

      Б)   3;

      В)  4.

 

 

3.      Матричная игра задана платежной матрицей A. Найти седловую точку игры.

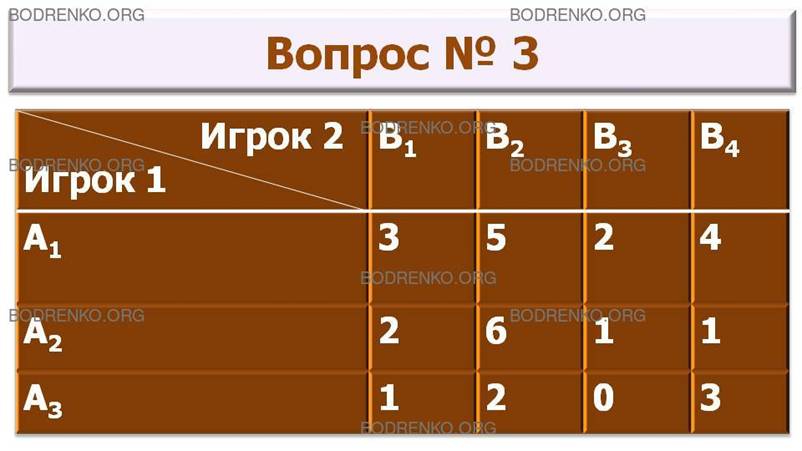
  A =

3	5	2	4
2	6	1	1
1	2	0	3

 

 

 

 

 

 

A) (А3, B2, 2);

 

      Б) (A1, B3, 2);

 

      В) игра не имеет седловой точки.

 

4.    Риском ИГРОКА при применении им стратегии Аi и при состоянии природы Qj называется:

А) разность между выигрышем ИГРОКА при применении им стратегии Ai и при состоянии природы Qj и минимальным выигрыш ИГРОКА при состоянии природы Qj;

           

Б) разность между максимальным выигрышем ИГРОКА при применении им стратегии Ai  и выигрышем ИГРОКА при применении им стратегии Аi и при состоянии природы Qj;

 

В) разность между максимальным выигрышем ИГРОКА при состоянии природы Qj и выигрышем ИГРОКА при применении им стратегии Аi и при состоянии природы Qj.

 

5. Колебанием выигрышей ИГРОКА при состоянии природы Qj называется:

 

А) разность между максимальным и минимальным выигрышами ИГРОКА при состоянии природы Qj;

 

Б) сумма максимального и минимального выигрышей ИГРОКА при состоянии природы Qj;

 

В) произведение максимального и минимального выигрышей ИГРОКА при состоянии природы Qj.

 

6. Показателем благоприятности состояния природы Qj называется:

 

А) минимальный выигрыш ИГРОКА при состоянии природы Qj;

 

Б) максимальный выигрыш ИГРОКА при состоянии природы Qj;

 

В) сумма максимального и минимального выигрышей ИГРОКА при состоянии природы Qj.

 

 

7. Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по максиминному критерию Вальда.

 

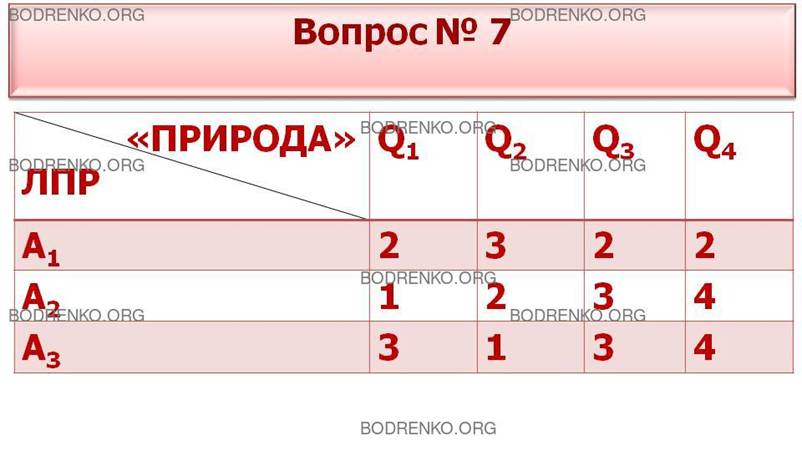
2	3	2	2
1	2	3	4
3	1	3	4

 

 

A =

 

 

 

A) A1;

Б) A2;

В) A3.

 

8. Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по критерию минимаксного риска Сэвиджа.

 

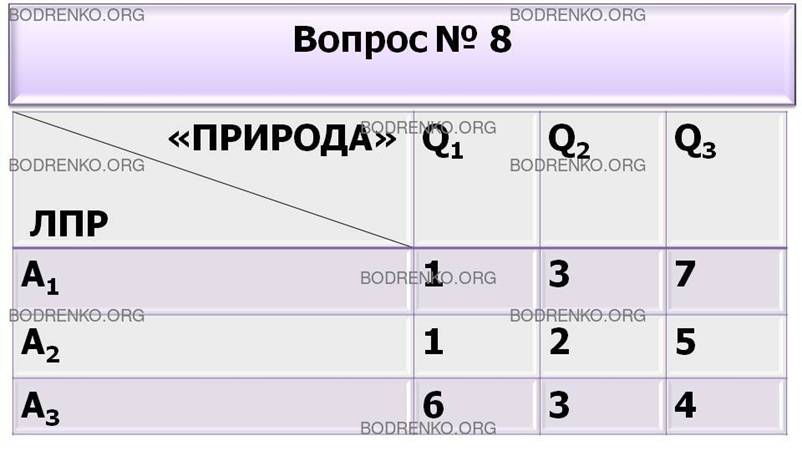
1	3	7
1	2	5
6	3	4

 

 

A = 

 

 

 

A) A1;

Б) A2;

В) A3.

 

9.  Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по критерию Лапласа относительно выигрышей (критерий «недостаточного  основания» Лапласа).

 

 

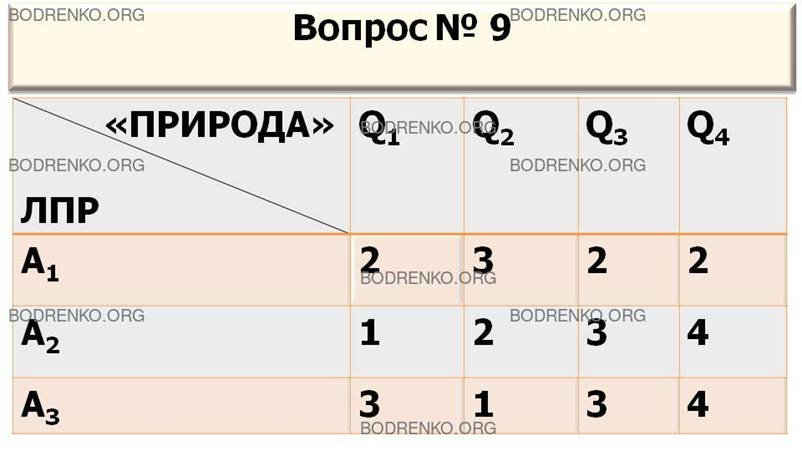
2	3	2	2
1	2	3	4
3	1	3	4

 A=

 

 

 

 

A) A1;

Б) A2;

В) A3.

 

10. Игра с природой задана платежной матрицей A. Найти оптимальную стратегию по критерию Лапласа относительно рисков.

 

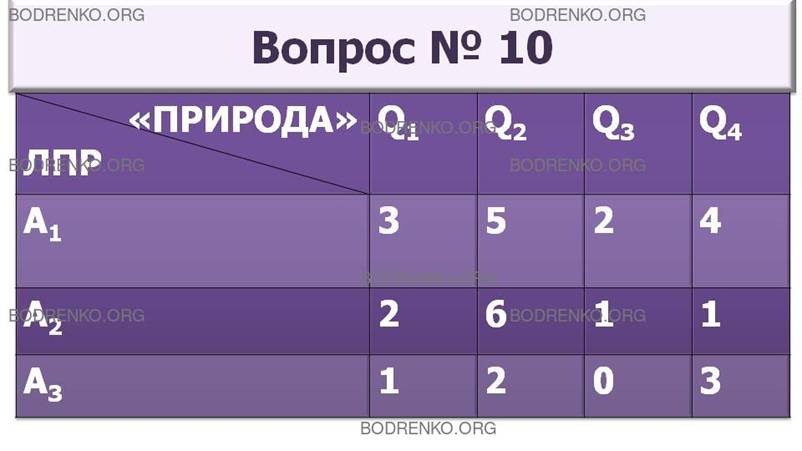
3	5	2	4
2	6	1	1
1	2	0	3

A =

 

 

 

 

 

 

A) A1;

Б) A2;

В) A3.