Методы оптимальных решений

 

Лекция 6

 

Тема лекции 6: «Теория графов и ее экономические приложения»

 

Разделы лекции:

 

1. Элементы теории графов.

2. Природа потоков в сетях и принцип их сохранения.

3. Теорема о максимальном потоке и минимальном разрезе.

 

РАЗДЕЛ 1. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ.

 

ЧТО ТАКОЕ ТЕОРИЯ ГРАФОВ?

 

Большинство возникающих в экономике за­дач удобно представлять для восприятия и анализа в виде сетей, которые позволяют ответить на два главных вопроса: до какого места необходимо дойти (цель) и какой путь следует избрать (как)?  Наглядность и логическая  обоснованность методов сетевого анализа позволяют выбрать довольно естественный подход к решению разнообразных экономических задач. Сетевые модели для людей, не занимающихся науч­ной работой, являются более понятными, чем другие модели, по­скольку для них все же лучше один раз увидеть, чем сто раз услышать. В значительной степени методы сетевого анализа ос­нованы на теории графов  –  области математики, началом разви­тия которой явилась задача о кенигсбергских мостах, сформулированная известным математиком Леонардом Эйлером в 1736 году.  Через реку Прегель, на которой стоял город Кенигсберг (в настоящее время – город Калининград), семь мостов (рисунок 1) связывали два острова друг с другом. Жителей Кенигсберга интересовал вопрос: можно ли в их городе совершить прогулку по замкнутому маршруту, проходя по каждому из семи мостов один и только один раз?  Леонард Эйлер математически сформулировал  и решил эту задачу.

 

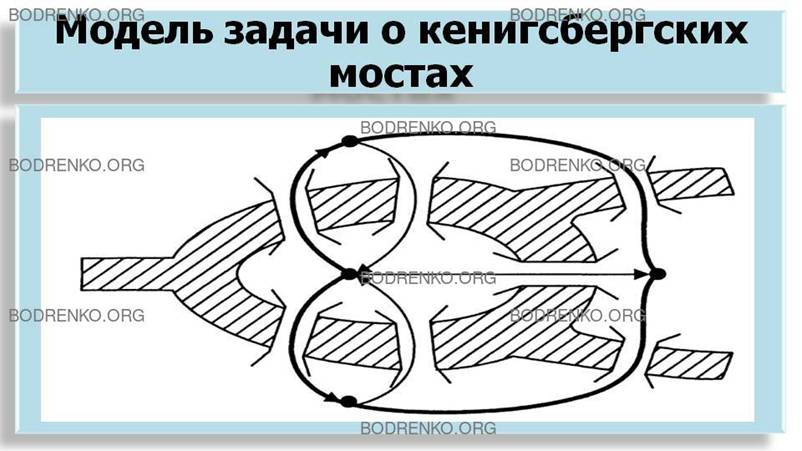
Рисунок 1.  Модель задачи о кенигсбергских мостах.

В девятнадцатом столетии в Англии возникла другая трудноразрешимая математическая  задача, имеющая прямое отношение к теории графов. Это задача о четырех красках: достаточно  ли четырех цветов для такой раскраски карты, нанесенной на плоскость или сферу, чтобы на ней не оказалось двух смежных областей одинакового цвета? Эта задача впоследствии была решена.

 

На основе исследования движения тока в электрических цепях Д. К. Максвелл и Г. Р. Кирхгоф сформулировали некото­рые принципы сетевого анализа. Были разработаны методы рас­чета наибольшей пропускной способности телефонных линий. В двадцатом столетии  теория графов прошла определенные стадии формирования и после 1930 года  была признана самостоятельной дисциплиной. В 40-х годах XX века в результате развития теории исследования операций был разработан ряд математических методов, необходи­мых для анализа больших систем. В 50-60-х годах XX века проводились работы по построению новых сетевых моделей и разработке алго­ритмов их решения на основе элементов теории графов.

МЕТОДЫ И МОДЕЛИ ТЕОРИИ ГРАФОВ И СЕТЕВОГО МОДЕЛИРОВАНИЯ. ОБЗОР ПРИМЕНЕНИЯ СЕТЕВЫХ МОДЕЛЕЙ.

 

Математический аппарат сетевых моделей базируется  на теории графов.  Используя простую терминологию, можно сказать, что граф характеризует отношения между множествами объектов, и теория графов направлена на исследование некоторых из многих возможных  в заданном представлении свойств этих объектов. В рамках теории исследования операций рассматривается большое количество практических задач, которые можно сформулировать и решить как сетевые модели. Приведем несколько конкретных примеров.  

 

1. Проектирование газопровода, соединяющего буровые скважины морского базирования с находящейся на берегу приемной станцией. Целевая функция соответствующей модели должна минимизировать стоимость строительства газопровода.  

 

2. Нахождение кратчайшего маршрута между двумя городами по существующей сети дорог.

 
3. Определение максимальной пропускной способности трубопровода для транспортировки сырой нефти от буровых скважин до нефтеперерабатывающих заводов.

4. Определение схемы транспортировки нефти от пунктов нефтедобычи к нефтеперерабатывающим заводам с минимальной стоимостью транспортировки.  

 

5. Составление временного графика строительных и т.п. работ (определение дат начала и завершения отдельных этапов работ).

 

ПРИМЕР 1. Значительное место в сетевом моделировании занимают зада­чи, связанные с планированием и составлением расписания вы­полнения работ или операций. Например, на рисунке 2 изображена сетевая модель комплекса работ по переводу торгового предприятия на самообслуживание. Обычно время и ресурсы выполнения каждой работы задают­ся вначале. Кроме того, прежде чем работа может начаться, все предшествующие ей работы должны быть завершены. Например, доставка оборудования (событие 15) является предшествующей работой (или опорной) для работы по монтажу оборудования. Следовательно, при наличии полного перечня работ комплекса сеть можно построить, если точно установлены предшествующие операции для каждой работы. В таких случаях сетевая модель представляет собой отражение логической взаимосвязи всех вхо­дящих элементарных работ в комплекс от начала до конца. Сете­вые графики представляют собой орграфы без контуров, дугам и вершинам которых приписаны числовые значения. Наибольшее распространение получил способ задания сетевых графиков в терминах дуги – операции, а вершины –   события.

 

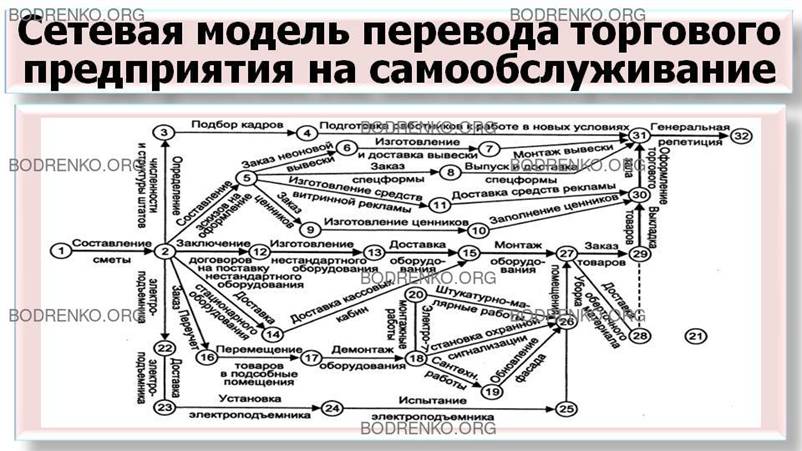
Рисунок 2. Сетевая модель перевода торгового предприятия на самообслуживание.

 

Исходное (1) — это такое событие, с которого начинается вы­полнение всего комплекса операций, а завершающее событие (32) соответствует достижению конечной цели. События обозна­чаются кружками, квадратами, ромбами или другими геометри­ческими фигурами.

ПРИМЕР 2. Одним из важных преимуществ сетевого моделирования яв­ляется возможность построения сетевых моделей, наглядно ото­бражающих процессы, например, коммерческой деятельности. Так, напри­мер, на рисунке 3 представлен ориентированный граф движения денежных потоков на счетах бухгалтерского учета, где в кружках указаны номера счетов бухгалтерского учета, а стрелками — про­водки.

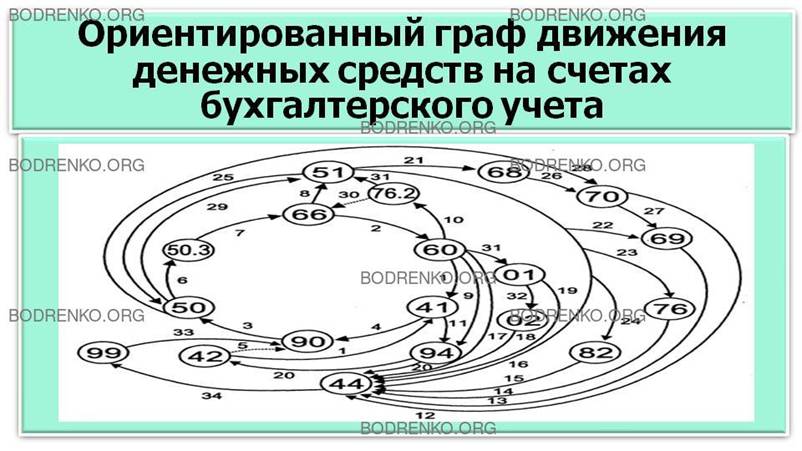
Рисунок 3. Ориентированный граф движения денежных средств на счетах бухгалтерского учета.

ПРИМЕР 3. ПЛАНИРОВАНИЕ РАБОТ КОММЕРЧЕСКОЙ ДЕЯТЕЛЬНОСТИ.

В коммерческой деятельности с целью исключения ущербов или неприятных неожиданностей необходимо составлять планы будущих работ, развернутых во времени. Любое множество работ связано отношениями предшествования. Причем каждая работа может быть начата, если все предшествующие ей работы будут за­вершены. В таких случаях сетевые методы позволяют решать как прямые, так и обратные задачи планирования работ коммерчес­кой деятельности. В результате решения прямых задач определяется оптималь­ный план комплекса работ при заданной схеме организации работ. Решение обратной задачи связано с поиском оптимального плана схемы организации работ, обеспечивающего максималь­ную эффективность.

 

Множество возникающих задач коммерческой деятельности можно свести к одной из трех наиболее типичных постановок за­дач оптимизации.

1. Какое максимальное количество средств и каким образом может быть высвобождено при заданной организации работ при условии, что общее время выполнения всего комплекса работ не возросло?

2. Как наилучшим образом использовать выделенные ограни­ченные ресурсы, чтобы время выполнения всего комплекса работ не превысило заданной величины?

3. Как распределить выделенные ресурсы между работами, чтобы время выполнения всего комплекса работ было бы мини­мальным?

При этом в исходных данных задач параметры работ могут быть заданы совершенно точно (детерминированный случай) или с некоторой степенью определенности, вероятности (стохас­тический случай). Решение задач этого класса также может быть решено методами се­тевого планирования. 

 

Задачи, вытекающие из перечисленных примеров, можно сформулировать и решать как задачи линейного программирования. Однако специфическая структура этих задач позволяет разработать специальные сетевые алгоритмы, более эффективные, чем стандартный симплекс-метод. Постановку и решение подобных задач можно получить с помощью методов сетевого моделирования. Решение приведенных задач (как и многих других подобных задач) требует применения различных сетевых оптимизационных алгоритмов.   

 

Перечислим наиболее известные сетевые оптимизационные алгоритмы.

 

1. Алгоритм нахождения минимального остовного дерева.

 

2. Алгоритм нахождения кратчайшего пути.

 

3. Алгоритм определения максимального потока.

 

4. Алгоритм минимизации стоимости потока в сети с ограниченной пропускной способностью.  

 

5. Алгоритм нахождения критического пути.  

 

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ.

Граф задается двумя множествами: непустым множеством X и множеством U, содержащим пары элементов из множества X. При этом элементы множества U могут повторяться, а также мо­гут повторяться элементы в парах. Граф, заданный на множествах (X,U), обозначается G=(X,U). Если элементы в парах множества U не упорядочены, то граф называется неориентированным, в противном случае — ориентированным, или орграфом. Элементы множества X называют вершинами графа, а элементы множе­ства U — ребрами для неориентированного графа и дугами для орграфа.

 

На плоскости граф задается в виде фигуры, состоящей из точек (вершин) и ли­ний, соединяющих некоторые из них (ребер или дуг).  Если на каждом ребре задается направление (т.е. каждая пара вершин, соединенная ребром, упорядочена), то граф называется ориентированным, в противном случае – неориентированным.

 

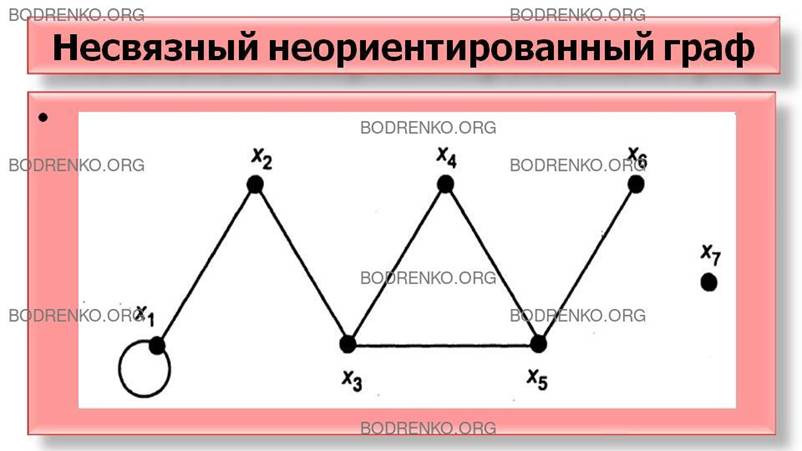
На рисунках 4, 5 изображены, соответственно, неориентированный и ориентированный графы.

Рисунок 4. Несвязный неориентированный граф.

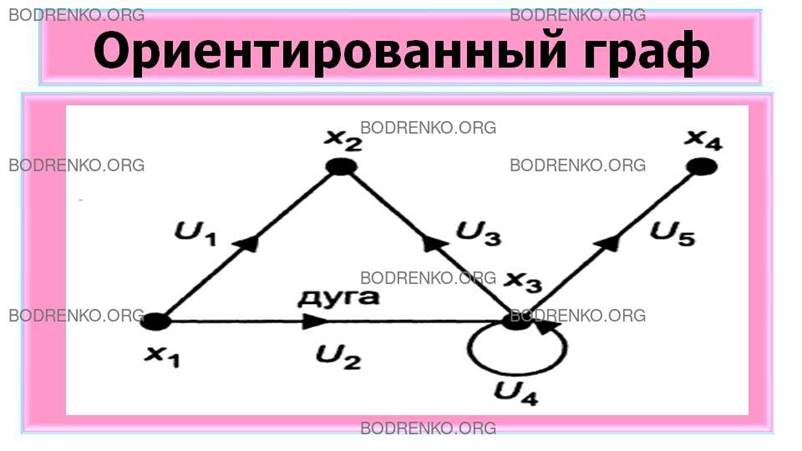
Рисунок 5. Ориентированный граф.

Неориентированный граф, изображенный на рисунке 4, имеет 7 вершин и 7 ребер. Для данного неориентированного графа (см.: рисунок 4) множество вер­шин X и ребер U можно записать так: X={x1, x2, x3, x4, x5, x6, x7}; U={(x1, x1), (x1, x2), (x2, x3), (x3, x4), (x3, x5), (x4, x5), (x5, x6)}.

 

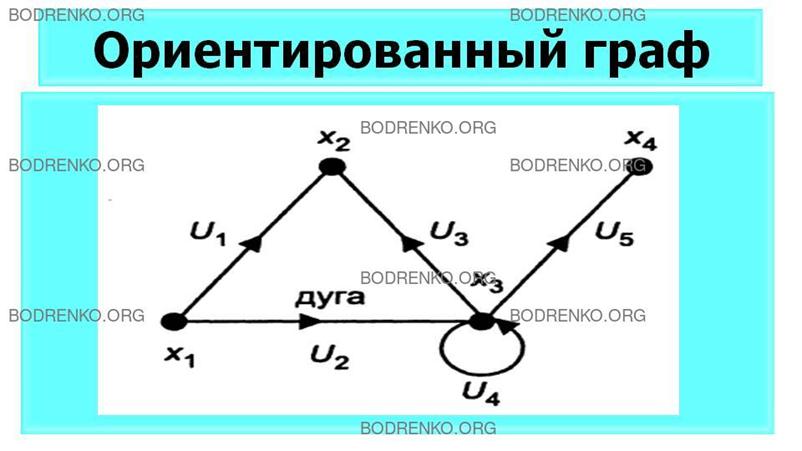
Ориентированный граф, изображенный  на рисунке 5, имеет 4 вершины и 5 дуг.  Множество вершин X и множество дуг U для данного графа (см.: рисунок 5) можно записать следующим образом: X={x1, x2, x3, x4}; U={(x1, x2), (x1, x3), (x3, x2), (x3, x3), (x3, x4)} (или U={U1, U2, U3, U4, U5}, где U1≡(x1,x2), U2≡(x1,x3), U3≡(x3,x2), U4≡(x3,x3), U5≡(x3,x4)).

Вершины графа называются смежными, или соседними, если сущест­вует ребро, их соединяющее.

 

Например, на рисунке 4 смежными являются следующие вершины: x1 и x2; x2 и x3; x3 и x4; x3 и  x5; x4 и x5; x5 и х6; вершины x3 и x6 — несмежные.

Маршрутом, или путем, соединяющим вершины A и B графа, называется такая последовательность его ребер, в которой каждые два соседних ребра имеют общую концевую точку, причем первое ребро выходит из вершины A, а последнее входит в вершину B (см. рисунок 6).

 

 

 

 

 

 

 

 

 

 

 

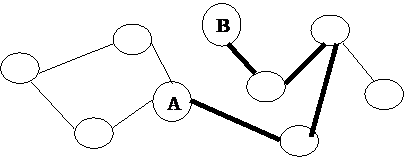
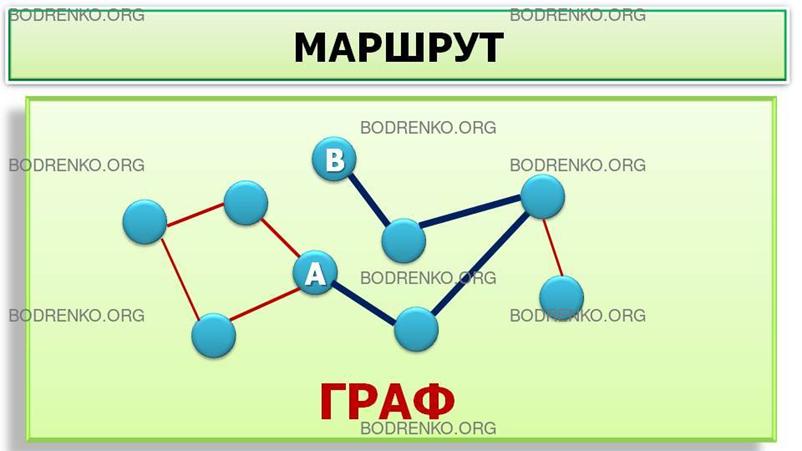
Рисунок 6. Маршрут.

 

В этом случае вершины A и B называются связанными.

 

Маршрут называется цепью, если каждое ребро графа встречается в нем не более одного раза (вершины в цепи могут повторяться и несколько раз) (рисунок 9).

 

Граф называется связным, если любая пара его вершин связана (рисунок 7).

 

 

 

 

 

 

 

 

 

 

Рисунок 7. Связный граф.

 

Граф, изображенный на рисунке 8, несвязен.

 

 

 

 

 

 

 

 

 

 

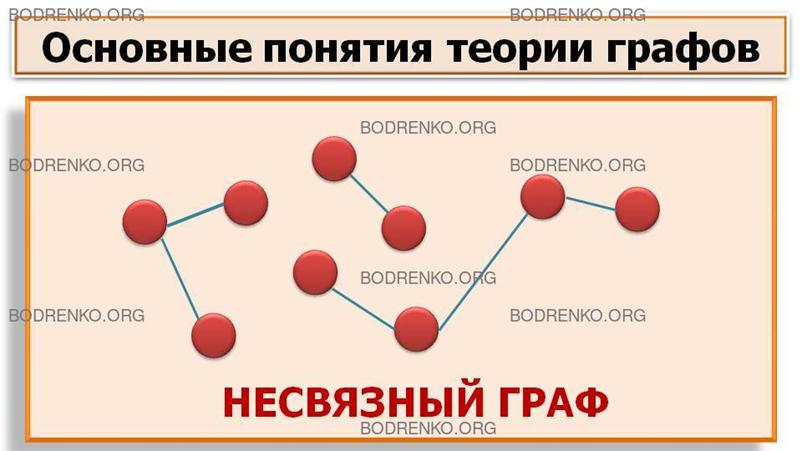
Рисунок 8. Несвязный граф.

 

Граф, представлен­ный на рисунке 4,  связный, а на рисунке 5 – несвязный, поскольку не существует цепи, соединяющей вершину x7 с осталь­ными.

 

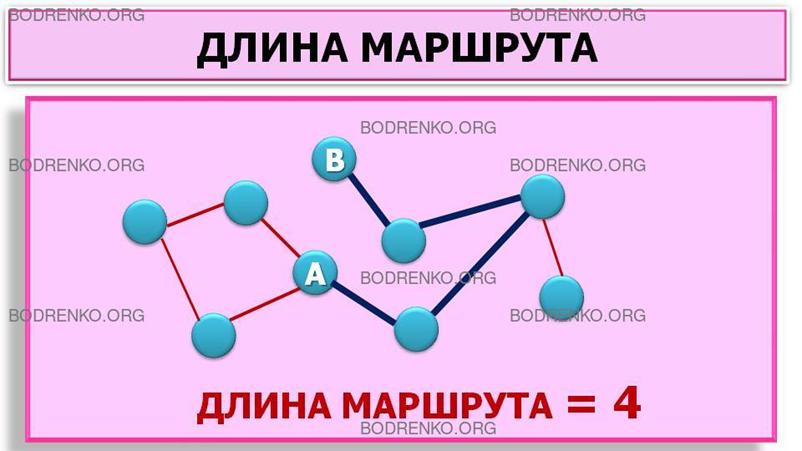
Число ребер в маршруте определяет его длину.

 

Например, на рисунке 6 изображен  маршрут, длина которого равна 4.

 

Простой цепью называется цепь, в которой все вершины различны.

 

 

 

 

 

 

 

 

 

 

 

 

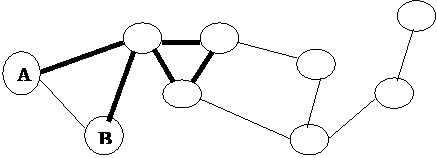
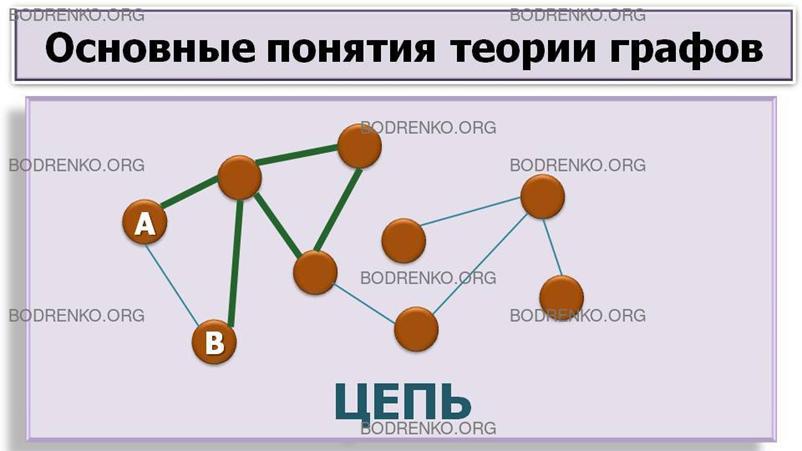
Рисунок 9. Цепь.

 

Цепь, начальная и конечная вершины которой совпадают, называется циклом (рисунок 10).

 

 

 

 

 

 

 

 

 

 

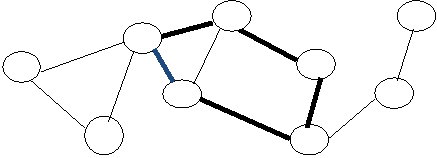
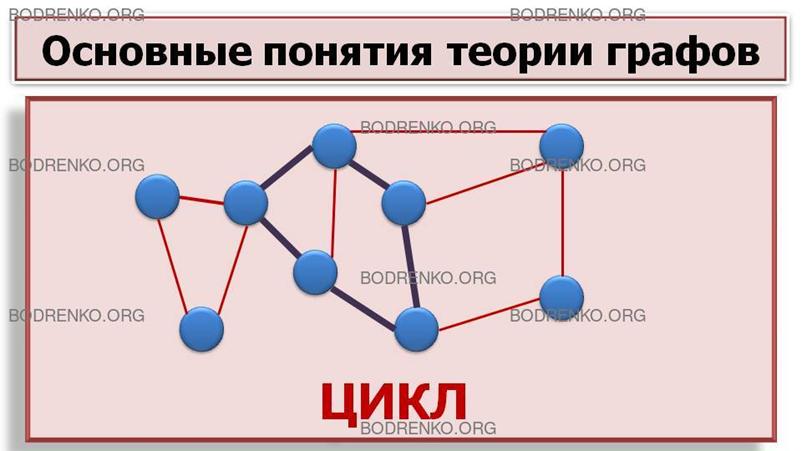
Рисунок 10. Цикл.

 

Простая цепь, начальная и конечная вершина которой совпадают, называется простым циклом. 

 

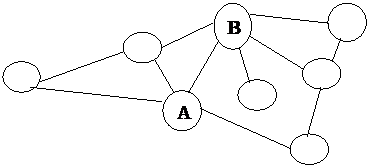
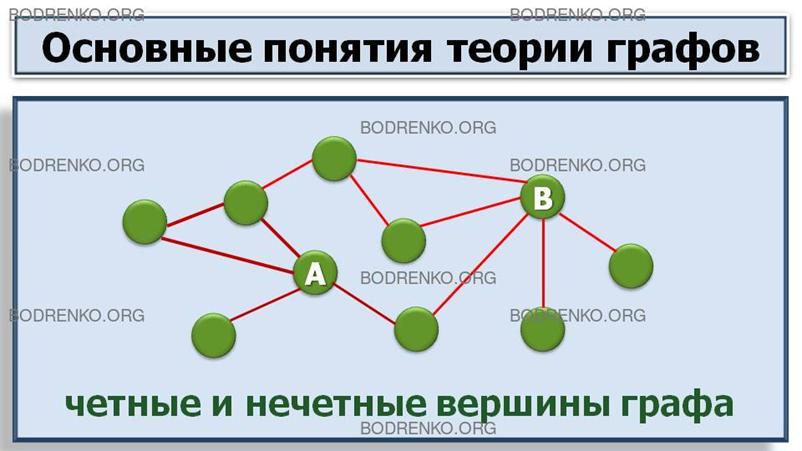
Вершина называется четной, если в ней сходится четное число ребер, и нечетной, если число всех сходящихся в ней ребер нечетно.

Вершина A на рисунке 11 четна — в ней сходятся 4 ребра, а вершина B нечетна — в ней сходятся 5 ребер.

 

 

 

 

 

 

 

 

 

 

Рисунок 11. Четные и нечетные вершины графа.

 

Ребро графа, начало и конец которого совпадают, называется петлей.

 

 

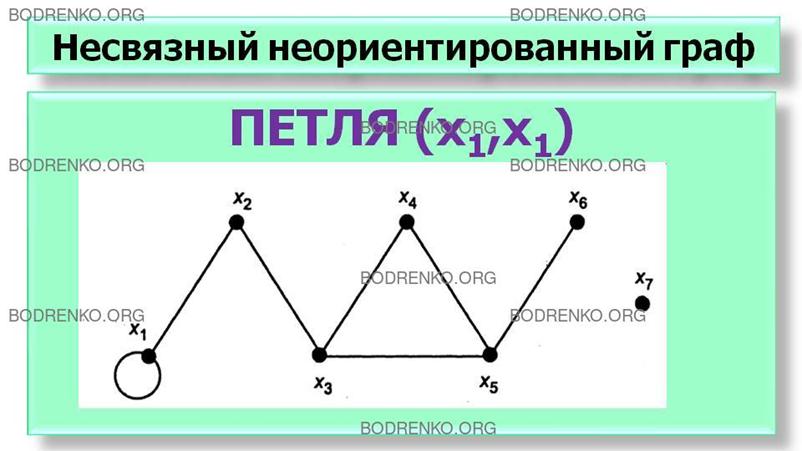
Например, на рисунке 4 изображена петля  (x1, x1).

Число ребер, сходящихся в вершине графа, называется степенью (порядком) этой вершины.

 

Степень вершины х обозначим через d(x).

 

Например, на рисунке 4:  d(x2)= 2; d(х3) = 3;  d(x4)= 2; d(х5)=3; d(x6)=1.

 

Вершина x, степень которой равна нулю: d(х) =0, называется изолированной вершиной (на рисунке 4 имеем: d(x7)=0). 

 

Вершина x, степень которой равна единице: d(x) = 1, называется висячей, или тупиковой (на рисунке 4 имеем: d(x6)=1).

Граф называется регулярным степени q, если все его вершины имеют степень q.

 

Регулярный граф, все вершины которого имеют степень 1, называется паросочетанием.

 

Граф называется двухдольным, если множество его вершин X может быть разделено на два непересе­кающихся подмножества Y и Z таким образом, что каждое ребро графа соединяет вершины из двух разных подмножеств Y и Z.

Расстоянием между вершинами A и B связного графа называется длина самой короткой цепи, соединяющей данные вершины.

 

Диаметром графа называется максимальное расстояние меж­ду его вершинами.

 

Граф называется конечным, если множество его ребер конечно. Примером бесконечного графа может служить прямоугольная сетка, заданная на всей плоскости.

ТЕОРЕМА (Эйлер). В любом конечном связном графе, все вершины которого четны, существует цикл, в котором каждое ребро графа участвует ровно один раз.

 

Такой цикл называют эйлеровым циклом, а граф, все вершины которого четны (и, значит, существует эйлеров цикл), — эйлеровым графом.

 

Важный класс графов составляют так называемые деревья.

 

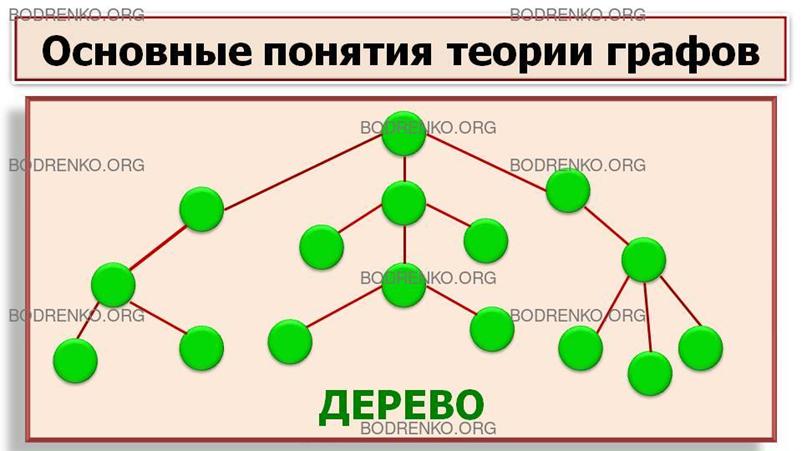
Деревом называется связный граф, который не имеет циклов (рисунок 12).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 12. Дерево.

 

Число B вершин дерева и число P его ребер различаются на единицу: B = P+1.

 

Таким образом, дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути  от исходной вершины к крайним вершинам называются ветвями.

 

Например, на рисунке 13 изображено дерево, имеющее 12 вершин и 11 ребер,  где вершина x1 является корнем дерева.

 

 

 

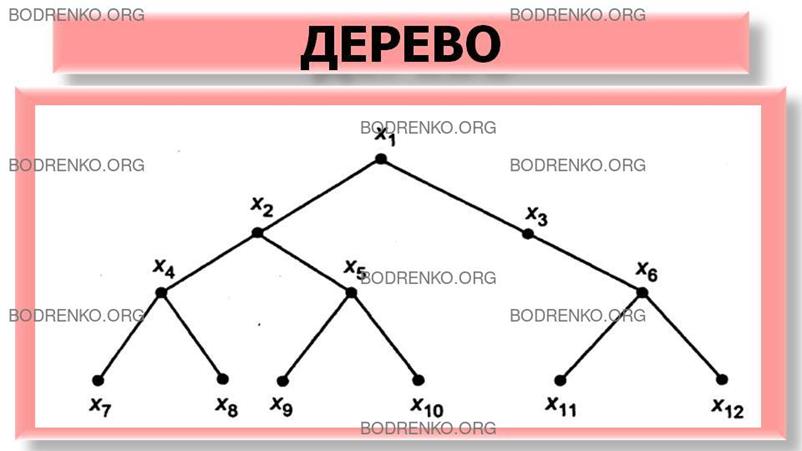
Рисунок 13. Дерево.

Лесом называется граф без циклов, представляющий собой совокупность деревьев (рисунок 14).

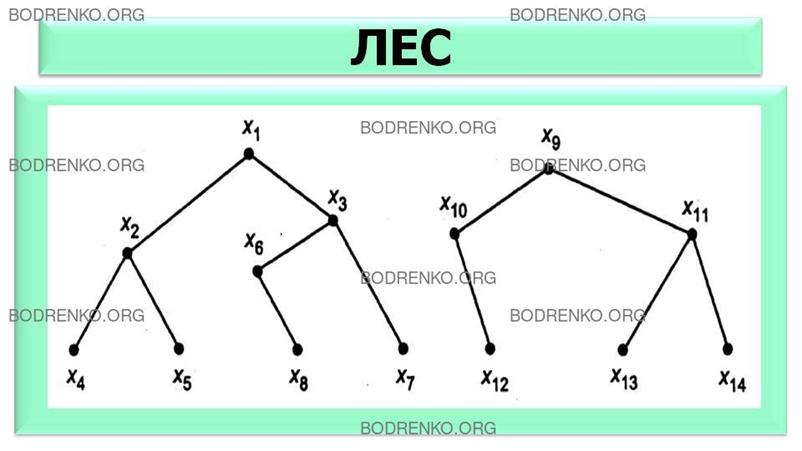
Рисунок 14. Лес.

Граф называется взвешенным, если каждому его ребру постав­лено в соответствие некоторое число, называемое весом ребра, на­пример расстояние между городами, стоимость или время проез­да между ними.

Подграфом графа G называется граф G1 с множеством вершин X1 и множеством ребер U1 такой, что Х1ÎX, U1ÎU. Для графа, изображенного  на рисунке 5, подграфом может быть граф G1=(X1, U1), где X1=(x1,x2, х3, x4, х5), а U1={(x1, x2), (x1, x3), (x3, x4), (x3, x5)}.

Компонентой связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа.

 

Например, граф, изображенный на рисунке 4, имеет две компоненты связности.

 

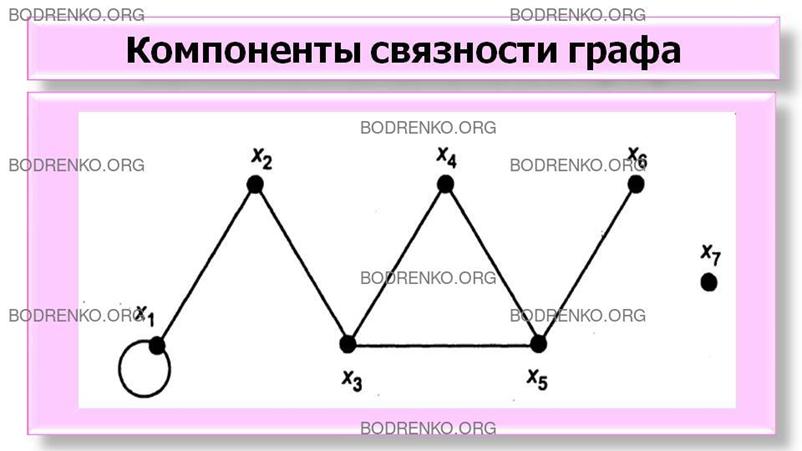
Вершина графа, удаление которой увеличивает число компо­нент связности, называется точкой сочленения. Под удалением вершины понимается удаление самой вершины и всех инцидентных ей ребер.

 

Точкой сочленения является, например, вершина x3 (см.:  рисунок 4), удаление которой приводит к появлению треть­ей компоненты связности.

Граф называется полным, если каждая вершина этого графа соединена ребром с любой другой его вершиной.

 

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа ровно один раз.

 

Например, для графа (рисунок 15) цепь, проходящая последовательно через вершины:  (6, 1, 5, 4, 3, 2, 8, 9, 10, 11, 12, 13, 14, 15, 20, 19,18, 17, 16, 7), является гамильтоновой.

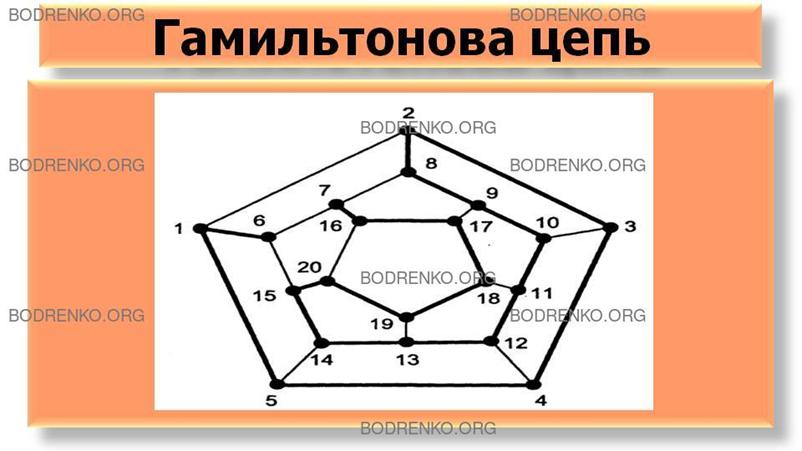
Рисунок 15. Гамильтонова цепь.

 

Гамильтоновым циклом называется гамильтонова  цепь, нача­ло и конец которой совпадают.

 

Например, если в конец предыдущей цепи добавить ребро, соединяющее вершину 7 с вершиной 6, (см.: рисунок 15), получим гамильтонов цикл.

Граф называется гамильтоновым, если в нем имеется гамильтонов цикл (рисунок 15).

Достаточные условия гамильтоновости неориентированного графа содержатся в следующей теореме.

 

ТЕОРЕМА (Дирак). Если в неориентированном графе G=(X,U) с n вершинами (n≥3) степень каждой вершины x не меньше чем n/2 (deg x ≥n/2, "xÎX), то граф G является гамильтоновым.

 

Термин «гамильтонов» связан с именем ирландского матема­тика У. Гамильтона, который в 1859 году предложил игру «Круго­светное путешествие». Каждой из двенадцати вершин додекаэдра (см.:  рисунок 13) соответствует один из городов мира. Необходи­мо, переезжая из города в город по ребрам додекаэдра, посетить каждый город только один раз и вернуться назад. Эта задача сво­дится к поиску простого цикла, проходящего через каждую вер­шину графа.

Задачи, касающиеся эйлеровых и гамильтоновых цепей и цик­лов, часто встречаются на практике. Например, стоимость выпол­нения комплекса коммерческих операций, работ существенно за­висит от последовательности, в которой они выполняются.

Например, задачу коммивояжера можно представить как в виде ориен­тированного (контур), так и неориентированного (цикл) графа (рисунок 16).

 

 

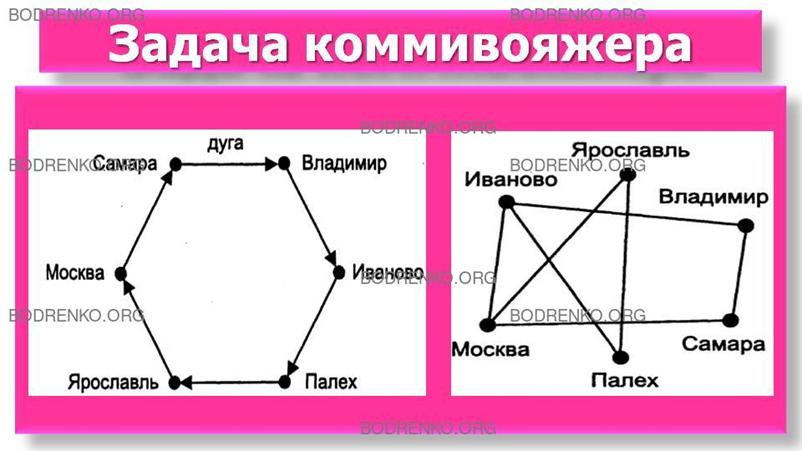
Рисунок 16. Задача коммивояжера.

 

Предложенный вариант решения задачи коммивояжера пред­ставляет собой кольцевой маршрут, где каждый город посещает­ся только один раз, начиная с любого населенного пункта.

 

ЗАМЕЧАНИЕ.  Для ориентированных графов используется термин контур (вместо термина цикл для неориентированного графа), термин дуга (вместо термина ребро для неориентированного графа).   Последова­тельность дуг, в которой конец предыдущей дуги совпадает с на­чалом следующей, называется путем. Длина пути определяется количеством в нем дуг. Путь называется простым, если в нем каждая дуга не встречается дважды, в противном случае он является состав­ным. Путь, в котором никакая вершина не встречается дважды, называется элементарным.  Путь, который начинается и заканчи­вается в одной и той же вершине, называется контуром.

Для ориентированного графа вместо степени вершины вво­дится понятие полустепеней исхода и захода. Если вершина явля­ется началом дуги, то дуга называется исходящей из вершины, если концом, то — заходящей. Полустепенью исхода вершины (d-(x)) называется число дуг, исходящих из этой вершины, полустепенью захода (d+(x)) называется число дуг, заходящих в вершину.

 

Например, для графа, изоб­раженного на рисунке 5, можно записать:

(d-(x2))=0, d-(x1)=2, (d+(x2))=2, (d+(x1))=0.

 

Известно несколько типов матриц, позволяющих задавать граф: матрица смежности, матрица инцидентности, матрица пропускных способностей.

ЧТО ТАКОЕ МАТРИЦА СМЕЖНОСТИ?

 

Матрица смежности графа с конечным числом вершин n представляет собой квад­ратную матрицу A=||aij|| порядка n, строки и столбцы которой соответствуют вершинам графа; и каждый элемент аij которой определяется по следующим формулам.

Для неориентированного графа значение элемента aij=k,  где k -число ребер, соединяющих вершины xi и xj.  В частности, если вершины xi и xj не соединены ни одним ребром, то aij=0.

Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.

 

Матрица смежности A неориентированного графа симметрична. Следовательно, все собственные значения матрицы A являются действительными числами, и существует базис из собственных векторов.

 

Множество собственных значений матрицы смежности A неориентированного графа называется спектром графа и является основным предметом изучения спектральной теории графов.   

 

Матрицы смежности для неориентированных графов являются основными структурами данных, которые используются для представления графов в компьютерных программах.

 

Для ориентированного графа элемент aij матрицы смежности A равен числу дуг, на­правленных от вершины i к вершине j (рисунок 17).

 

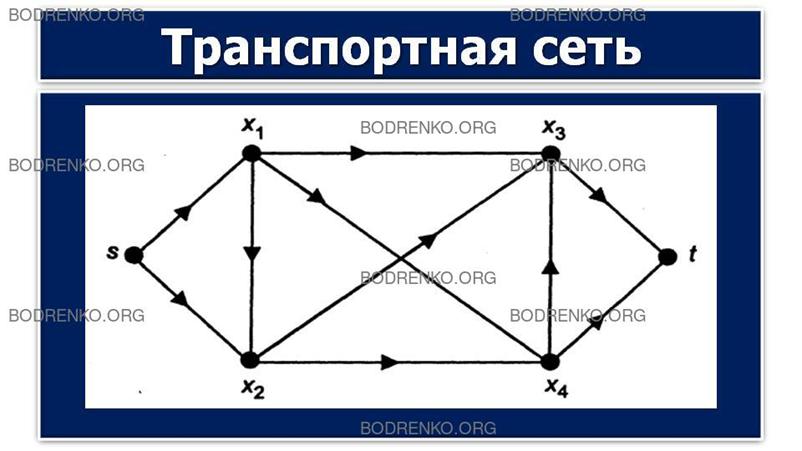
Рисунок 17. Транспортная сеть.

 

Для неориентированного графа, представленного на рисунке 4, матрица смежности симметрична, имеет порядок 7 и за­писывается в следующем виде.

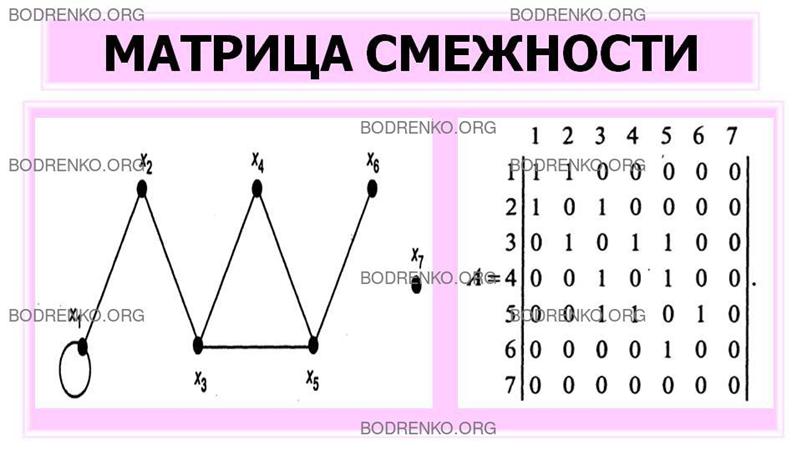
Слева и сверху проставлены номера вершин.

Для ориентированного графа, изображенного на рисунке 17, ма­трица смежности  квадратная порядка 6,  и записывается в следующем виде.

 

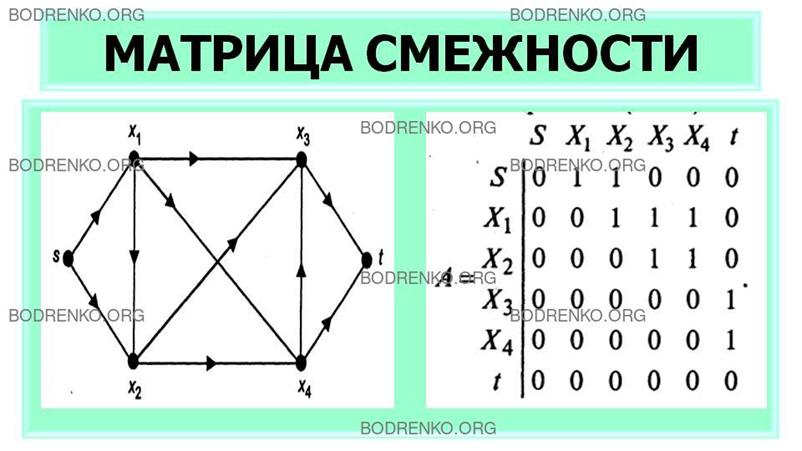
Матрицу смежности чаще применяют для задания неориенти­рованного графа в компьютерных программах. Для задания ориентированного графа лучше ис­пользовать матрицу инцидентности.

 

ЧТО ТАКОЕ МАТРИЦА ИНЦИДЕНТНОСТИ?

 

Матрица инцидентности графа – одна из форм представления графа, в которой указываются связи между инцидентными элементами графа: вершинами и ребрами (дугами) графа. Строки матрицы инцидентности B соответствуют вершинам, а столбцы – ребрам (дугам).

 

Матрицей инцидентности B ориентированного графа с n вершинами и m дугами называется матрица B=||bij|| размера (n x m) с n стро­ками и m столбцами, элементы которой bij определяются по следующим формулам.

Столбец, соответствующий дуге (i,j) графа, заполняется следующим образом: в строке, соответствующей вершине i, ставится (- 1), в строке, соответствующей вершине j, ставится 1, в остальных ячейках ставится 0.  

 

То есть bij= - 1,   если вершина  является началом дуги (i,j);

bij = 1, если вершина  является концом дуги (i, j);

bij=0, если вершина и дуга не инцидентны.

Для неориентированного графа элемент bij=1, если вершина и ребро инцидентны, и bij=0 в противном случае.

 

Для ориентированного графа, представленного на рисунке 17, матрица инцидентности  B  имеет следующий вид.

 

Ненулевое значение в соответствующей ячейке матрицы инцидентности указывает связь между вершиной и ребром (дугой) графа – их инцидентность.

 

В каждом столбце матрицы инцидентности B ориентированного графа обязательно должны стоять (-1)  и 1 (остальные элементы равны 0, если граф имеет более 2-х вершин).

 

В каждом столбце матрицы инцидентности B неориентированного графа обязательно должны стоять две единицы (остальные элементы равны 0, если граф имеет более 2-х вершин).

 

Направленный граф – это ориентированный граф, в котором любые две вершины соединены не более чем одной дугой.

 

Взвешенный ориентированный граф без петель, в котором выделено k вершин, называемых полюсами, называется k-полюсной цепью.

 

Среди сетей особо выделяется двухполюсная транс­портная сеть (рисунок 17) S = (N, U) с множеством вершин N и множеством дуг U, для которых выполняется следующее условие:

1) существует только одна вершина sÎN сети S, в которую не заходит ни одна дуга. Эта вершина называется входом, или исто­ком (источник), сети;

2) существует только одна вершина tÎN сети S, из которой не выходит ни одной дуги сети. Эта вершина называется выходом, или стоком, сети;

3) каждой дуге uÎU сети S поставлено в соответствие неотрица­тельное число c(u), называемое пропускной способностью дуги.

 

 

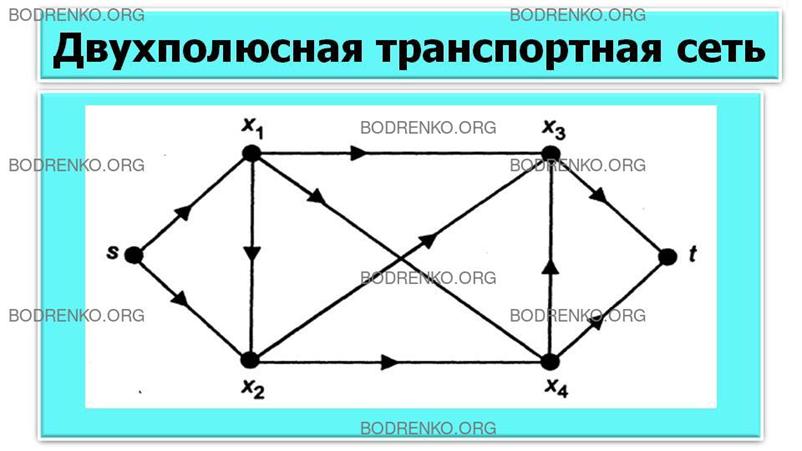
Сетью будем называть ориентированный конечный связный граф без циклов и петель, имеющий начальную вершину (источник) и конечную  вершину (сток).

 

 

Примерами вершин сети могут быть пересечения автострад, электростанции, телефонные узлы, железнодорожные узлы, аэропорты, водохранилища, товарные склады. Примерами дуг сети могут быть дороги, линии электропере­дачи, телефонные линии, авиалинии, водные магистрали, нефте- и газопроводы и т.д.

РАЗДЕЛ 2. ПРИРОДА ПОТОКОВ В СЕТЯХ И ПРИНЦИП ИХ СОХРАНЕНИЯ.

Сходство сетевых представлений наблюдается в природе, тех­нике и различных сферах деятельности человека. Так, например, с высоты птичьего полета или самолета можно наблюдать сетевую модель формирования реки, например Волги, от ее истоков ма­ленькие ручейки и реки, соединяясь во взаимосвязанные артерии, объединяются в одно большое русло, по которому потоки воды ус­тремляются в Каспийское море. Такие же аналогии представляют собой сети железных дорог, по которым транспортные потоки на­правляются из пунктов отправления в пункты назначения, осуще­ствляя перевозку потоков грузов и пассажиров. Совокупность ли­ний электропередач также представляют собой энергетическую сеть, по которой потоки электроэнергии от электростанций по проводам поступают к потребителям. Автомобильные дороги как в масштабе города, района, области, так и в более крупных мас­штабах страны или, например, континента, представля­ют собой сети, по которым движутся потоки автомобилей. Нефте- и газопроводы в совокупности представляют собой сети трубо­проводов, по которым потоки нефти или газа поступают от источ­ников к потребителям. Водопроводные сети обеспечивают движе­ние потоков воды по трубопроводам от источников к потребите­лям. Аналогичные сети представляют собой маршруты движения кораблей и самолетов, обеспечивающие перемещение потоков пассажиров и грузов по планете. Такие же аналогии представляют собой телефонные, радио- и телекоммуникационные сети, по ко­торым циркулируют информационные потоки, например ком­пьютерные сети связи различного назначения. Особый интерес представляют сети, образованные движением товарных и финансовых потоков, изучение которых может пояснить очень многие явления нашей жизни.

Перечисленные сетевые аналогии потоковых процессов име­ют динамический характер, связанный с перемещениями различ­ных по своей природе масс в пространстве: электроэнергии, неф­ти, газа, воды, воздуха, железнодорожного, воздушного, авто­мобильного транспорта, товаров, финансов, пешеходов, инфор­мации и т.п. Причем существование этих потоков необходимо для обеспечения и поддержания жизнедеятельности человека. Сетевое представление взаимодействия и циркуляции потоков необходи­мо, чтобы оценить и вычислить разные характеристики, описывающие условия существования и поведения потоков в таких средах. Множество возникающих в таких случаях задач может быть решено с помощью теории потоков в сетях. В этой теории в качестве основы рассматриваются движения в сетях потоков лю­бой природы от источника s к стоку t.

ОПРЕДЕЛЕНИЕ. Потоком в сети S=(N,U) от входа sÎN к выхо­ду tÎN называется неотрицательная функция φ=φ(i,j), определенная на множестве дуг (i,j)ÎU сети S, со следующими свойствами:

1) ВЕЛИЧИНА ПОТОКА ПО КАЖДОЙ ДУГЕ НЕ ДОЛЖНА ПРЕВОСХОДИТЬ ЕЕ ПРОПУСКНОЙ СПОСОБНОСТИ: 0≤φ(i,j)≤c(i,j);  (i,j)ÎU;

2) ВЕЛИЧИНА ПОТОКА, ВХОДЯЩЕГО В КАЖДУЮ ВЕРШИНУ СЕТИ, ЗА ИС­КЛЮЧЕНИЕМ ВХОДА И ВЫХОДА, РАВНА ВЕЛИЧИНЕ ПОТОКА, ВЫХОДЯЩЕГО ИЗ ЭТОЙ ВЕРШИНЫ:

∑       φ-(i,j) – ∑  φ+(j,i) = 0, i≠s, j≠t,

jÎNi               jÎŇi

 

где Ni — множество вершин, инцидентных дугам, направленным от вершины i (исходящие из вершины i дуги);

Ňi - множество вершин, инцидентных дугам, направленным к вершине i, (входящие в вершину i дуги).

Из определения потока следует, что величина потока не исче­зает и не накапливается в вершинах сети.

 

Следовательно, коли­чество потока из входа s равно количеству потока, заходящему в выход t. ЭТО ЗНАЧЕНИЕ НАЗЫВАЕТСЯ ВЕЛИЧИНОЙ ПОТОКА V.

 

Таким об­разом, поток в сети сохраняется, а величина потока V равняется сумме значений потоков, выходящих из вершины s: ∑φ-(s,j), или входящих в вершину t: ∑φ+(j,t). То есть

 

V =  ∑ φ-(s,j)  =  ∑  φ+(j,t),

     jÎNs             jÎŇt

где Ns – множество вершин, инцидентных дугам, направленным от источника s (исходящие из источника s дуги);

Ňt – множество вершин, инцидентных дугам, направленным к выходу t, (входящие в сток t дуги).

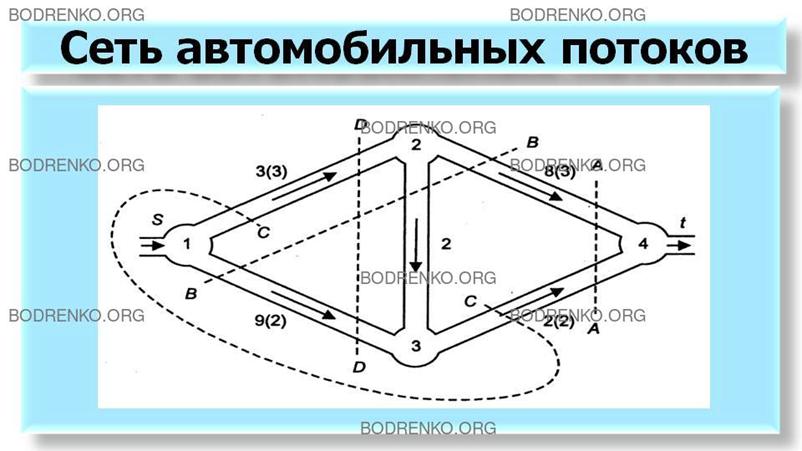
На рисунке 18  изображена сеть автомобильных потоков, которая представляет ориентированную сеть S = (N, U) имеющую множество вершин N = {1, 2, 3, 4} и множество дуг U ={(1, 2); (2,3); (2, 4); (1,3); (3,4)}.

 

Рисунок 18. Сеть автомобильных потоков.

Количественные характеристики дуг сети, а также взаимо­связь между ее вершинами могут быть представлены с помощью матрицы расстояний L=||lij|| или матрицы стоимостей C=||cij||.

Для ориентированной сети, представленной на  рисунке 18, матрица смежности имеет следующий вид.

 

Матрица инцидентности ориентированной сети, изображенной на  рисунке 18,  имеет следующий вид.

 

 

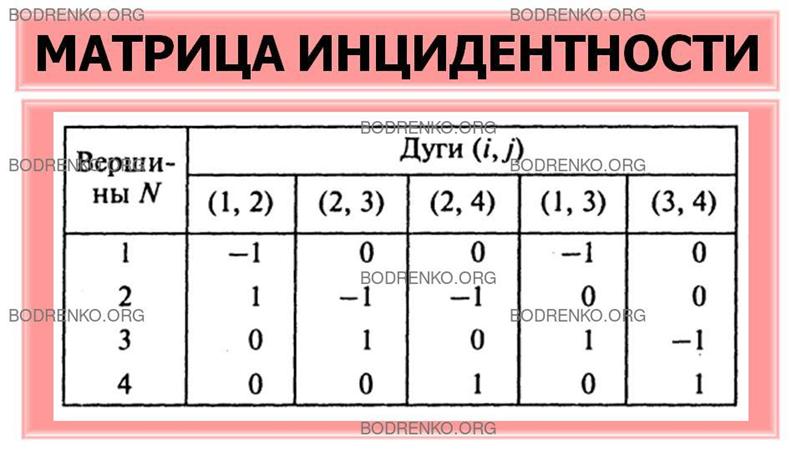
На рисунке 18 стрелками показано направление односторонне­го разрешенного движения потоков автомобилей. От одного пе­рекрестка i до другого перекрестка j пропускная способность c(i, j) по дуге (i, j) по каж­дой улице ограничена и определяется максимально допус­тимой скоростью движения, например, 60 км/ч. В связи с этим мощность автомобильного потока φ(i,j) не может превысить допустимую – пропускную способность c(i,j). Таким образом, должно выполняться первое свойство потока, условие существования статичес­кого или устойчивого потока для каждой улицы:

0≤φ(i,j)≤c(i,j);  (i,j)ÎU.

Рассматривая взаимодействие ограничений по каждой улице и в совокупности по всем перекресткам (вершинам сети), условие сохранения потока в этой сети запишем следующим образом:

∑ φ-(i,j) – ∑  φ+(j,i) =0; i≠s; j≠t.

jÎNi             jÎŇi

 

Для источника сети при i=s нет входящих потоков, следова­тельно,

 

V=  ∑  φ-(s, j).

     jÎNs

 

Для стока при j=t нет выходящих потоков, следовательно,

 

V = ∑ φ+(j,t).

    jÎNt

 

ПРИМЕР 4. Рассмотрим пример анализа сети S = (N,U), представленной на рисунке 19.  N= {s, 1, 2, 3, 4,..., t}; U = {(s, 1); (s,3); (1,2); (1,3); (2,t); (3,2); (3,4); (4,t)}.

 

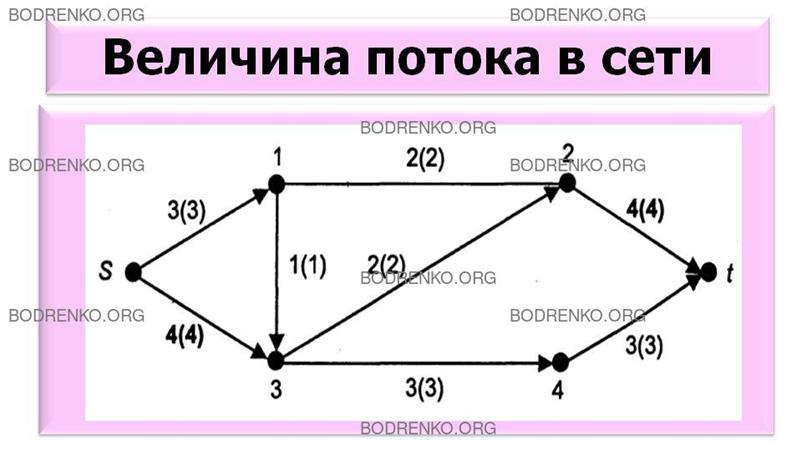
Рисунок 19. Величина потока в сети.

Пропускная способность указана над каждой дугой, где рядом в скобках указано значение существующего потока. Свойства по­тока в данном случае выполняются, поскольку указанные величи­ны не превышают пропускных способностей дуг в каждой вершине, отличной от входа и выхода, поток сохраняется. Например, в вершину 2 заходят 4 единицы потока по дугам (1, 2) и (3, 2) и вы­ходят 4 единицы по дуге (2,t).  Величина потока в сети составляет V=3+4=7 и сохраняется.

РАЗДЕЛ 3. ТЕОРЕМА О МАКСИМАЛЬНОМ ПОТОКЕ И МИНИМАЛЬНОМ РАЗРЕЗЕ.

Пусть в ориентированной сети S= (N, U) от источника к сто­ку протекает поток, величина которого равна V. Поскольку про­пускная способность каждой дуги c(i, j) является величиной ко­нечной, то максимальная величина допустимого потока всей сети тоже ограничена. Максимальный поток сети определяется на основе одного из основных понятий теории сетей — понятия раз­реза. Введем понятие разреза.

Множество вершин N сети S=(N,U) можно разбить на два непересекающихся подмножества Np и Ňp, которые соединяются между собой дугами, образующими МНОЖЕСТВО ДУГ РАЗРЕЗА Up, Причем исток s принадлежит множеству вершин Np: sÎNp, а сток t при­надлежит множеству Ňp: tÎŇp. Тогда величина потока из мно­жества Np во множество Ňp,  протекающего по дугам Up,  не может быть больше, чем сумма пропускных способностей дуг этого множества, что можно записать таким образом:

Этот барьер для потока, отделяющий множество вершин Np, от множества вершин Ňp, называется разрезом и обозначается (Np, Ňp).

 

Разрез представляет такое множество дуг Up, исключе­ние которых отделяет вход s от выхода t сети, и, следовательно, от­деляет множество Np от Ňp  сети S=(N,U) таким образом, что су­ществование потока в таком случае невозможно и тогда величина потока в сети V = 0. Причем начало дуги разреза принадлежит множеству Np, а конец - Ňp. Таким образом, в разрез входят дуги, соединяющие верши­ны этих множеств.

Величина максимального потока от источника s к стоку t ог­раничена сверху величиной разреза C(Np, Ňp), определяемой сум­мой пропускных способностей всех входящих в него дуг множе­ства Up.   Следовательно, V≤ C(Np, Ňp).

 

Минимальным разрезом се­ти называется разрез, имеющий минимальную величину C(Np,Ňp).

 

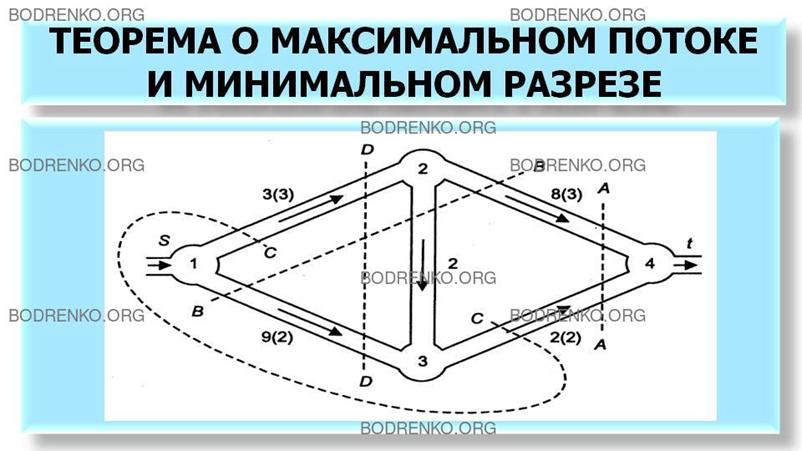
В соответствии с теоремой о максимальном потоке и минималь­ном разрезе, сформулированной Фордом и Фалкерсоном, величи­на максимального потока Vmax  от входа s (источника) в выход t (сток) равна величине минимального разреза, отделяющего вход и выход сети.

 

Следовательно,

 

Vmax  = min C(Np, Ňp).

           UpÎU

Таким образом, разрез определяет множество дуг, при удалении которых из сети полностью прекращается поток от источника к стоку. Пропускная способность разреза равна сумме пропускных способностей «разрезанных» дуг. Среди всех разрезов сети разрез с минимальной пропускной способностью определяет максимальный поток в сети.

Рассматриваемые сети являются сетями с ограниченной про­пускной способностью и имеют распространение в реальной жизни. Это послужило поводом к появлению и постановке задач о максимальном потоке разной природы, связанных с определе­нием максимально допустимой величины Vmax при соблюдении ус­ловий, записанных в виде системы уравнений и неравенств.

В сформулированной выше задаче для сохранения потока ав­томобилей (см.:  рисунок 18), например, через перекресток (3) необ­ходимо, чтобы поступающие потоки автомобилей к этой верши­не (3) φ(1, 3) и φ(2, 3) равнялись величине потока, вытекающего из этой вершины φ(3, 4), что можно записать так:

φ(1,3) + φ(2,3)≤φ(3,4).

Аналогичные уравнения можно записать для остальных вер­шин сети. Поскольку задача заключается в определении макси­мально возможного потока в сети, то необходимо последователь­но вычислить потоки через все разрезы и выбрать из них мини­мальный.

Разрез (А, А) на рисунке 18 отделяет источник (1) от стока (4), в данном случае вершину (4) от остальных вершин (1, 2, 3). Вели­чина разреза определяется пропускной способностью входящих в него дуг (2, 4) и (3, 4) и соответственно равна:  С(2, 4) + С(3, 4)=2+8=10. Затем можно определить все другие возможные ва­рианты разрезов (В,В) (D,D) и (С,С). Тогда величина максималь­ного потока от источника к стоку равна величине минимального разреза:

Vmax= min {(A,A), (B,B), (C,C), (D,D)}= min {10; 12; 19; 5} = 5.

Из рисунка 18 видно, что после удаления дуг разрезов перестают существовать пути движения потока от входа сети s к выходу t. Разрезы имеют раз­личные пропускные способности. Разрез, имеющий минимальную пропускную способность, называется минимальным разре­зом сети.

Приведенный вариант анализа фрагмента сети автомагистра­ли указывает на возможность применения приведенного прин­ципа сохранения потока в коммерческой деятельности. Это поз­волит своевременно принимать оптимальные управленческие решения и облегчить оперативное вмешательство по регулирова­нию не только автомобильных, но и финансовых или товарных потоков.

Рассмотренные алгоритм и примеры моделирования позво­ляют решать аналогичные по своей природе задачи, например по бесперебойному снабжению потоками электричества, бензина, газа, мазута, нефти, воды, продовольственными и непродоволь­ственными товарами населенных пунктов, и таким образом пре­дупредить появление критических ситуаций.

ПРИМЕР 5 (ЗАДАЧА О МАКСИМАЛЬНОМ ПОТОКЕ).

 

 Рассмотрим сеть трубопроводов для транспортировки сырой нефти от буровых скважин до нефтеперерабатывающих заводов. Для перекачки нефти предусмотрены магистральные насосные станции. Каждый сегмент трубопровода имеет свою пропускную способность. Сегменты трубопровода могут быть как однонаправленные (осуществляют перекачку нефти только в одном направлении), так и двунаправленные. В однонаправленных сегментах положительная пропускная способность предполагается в одном направлении и нулевая в другом. На рисунке 20 показана типовая сеть нефтепроводов. Как определить максимальную пропускную способность (т.е. максимальный поток) между нефтяными скважинами и нефтеперерабатывающими заводами? При решении данной задачи исходную сеть необходимо свести к сети с одним источником и одним стоком. Этого можно достигнуть путем введения дополнительных дуг с бесконечной пропускной способностью от источника к скважинам и от нефтеперерабатывающих заводов к стоку (на рисунке 20 эти дуги показаны пунктирными линиями). 

 

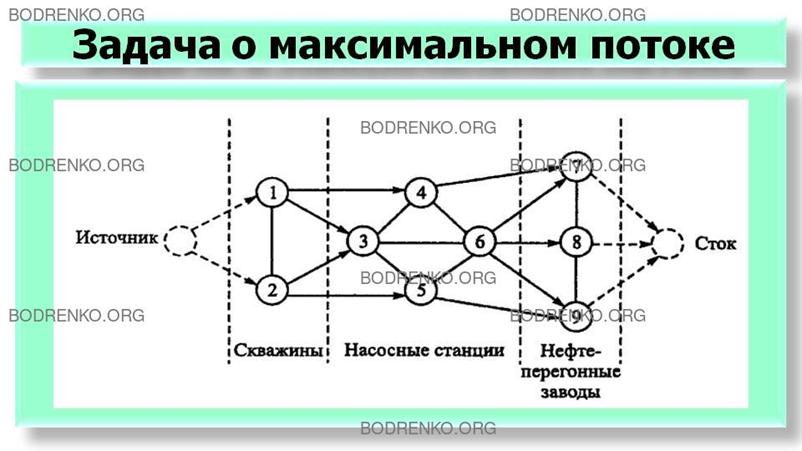
Рисунок 20. Задача о максимальном потоке.

 

Математическая модель задачи о максимальном потоке вы­глядит следующим образом.

Рассмотрим двухполюсную сеть S = (N, U) с одним входом (источником) sÎN  и одним выходом (стоком) tÎN. Дуги сети (i,j)ÎU  и имеют ограниченную пропускную способность cij. Задача о мак­симальном потоке заключается в поиске таких потоков φ(i,j) по ду­гам (i,j) сети, что результирующий поток из источника s в сток t яв­ляется максимальным.

Требуется найти такие значения потоков φ(i,j), при которых

V=  ∑  φ+(s,j) = ∑  φ-(j,t) →max,

        j                   j

 

при ограничениях:

0≤φ(i,j)≤cij,

 

∑ φ(i,j) – ∑ φ(j,i)=0.

j            j

 

 

Для решения этой задачи может быть использован метод по­строения увеличивающих цепей.

ПРИМЕР 6. ЗАДАЧА О ПОТОКЕ МИНИМАЛЬНОЙ СТОИМОСТИ.

Задача нахождения потока наименьшей стоимости в сети с ограниченной пропускной способностью обобщает задачу определения максимального потока по следующим направлениям.

 

1 . Все ребра допускают только одностороннее направление потока, т.е. являются (ориентированными) дугами.

 

2. Каждой дуге поставлена в соответствие (неотрицательная) стоимость прохождения единицы потока по данной дуге.

 

3. Дуги могут иметь положительную нижнюю границу пропускной способности.

 

4. Любой узел сети может выступать как в качестве источника, так и стока.

В рассматриваемой задаче необходимо найти потоки по дугам, минимизирующие общую стоимость прохождения потока по сети; при этом должны удовлетворяться ограничения на пропускные способности дуг и на величины предложений и спроса отдельных (или всех) узлов. 

 

Математическая модель задачи имеет следующий вид.

 

Пусть дана двухполюсная сеть S=(N,U) с источником s и стоком t. Для каждой дуги (i,j)ÎU заданы пропускная способность сij и стоимость доставки по ней единицы потока rij. Необходимо най­ти поток от источников в сток заданной величины V, имеющей минимальную стоимость доставки. Очевидно, при этом поток V не должен превышать максимальной величины Vmax.

Требуется минимизировать функцию R:

 

R =∑∑rij∙φij → min

     i  j 

 

при ограничениях:

 

 

ПРИМЕР 7. ТРАНСПОРТНАЯ ЗАДАЧА.

Транспортная задача является одной из первых потоковых за­дач, которая была сформулирована и решена в 1941 году Ф. Хичко­ком, а затем стала применяться в различных задачах перевозки и распределения. В этой задаче рассматриваются предложение грузов (товаров) от m поставщиков в объемах a1, a2, ... , am  и спрос от n покупателей в объемах b1,  b2,..., bn, затраты на перевозку единицы груза от i-го поставщика к j-му покупателю составляют cij, а объемы перевозимых грузов соответственно составляют хij,  которые необходимо определить. Математическая модель имеет следующий вид.

Определить такие объемы перевозок

хij = ?, i=1, …, m, j=1, …, n,

 

которые при условиях-ограничениях:

 

обеспечивали бы минимальные затраты на перевозку в соответст­вии с целевой функцией:

 

 

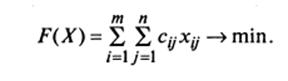
Модель этой задачи может быть представлена в виде сети (рисунок 21), если вершинам поставить в соответствие поставщи­ков и покупателей, а ориентированным дугам — пути для перевозки грузов.

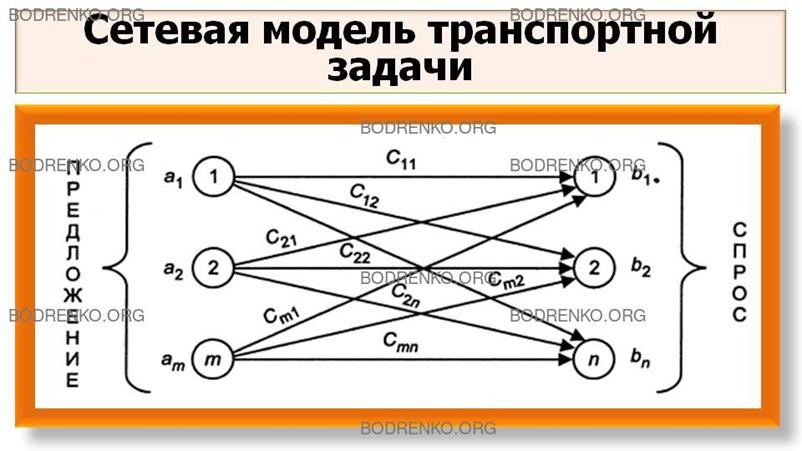
Рисунок 21.  Сетевая модель транспортной задачи.

Эта задача является частным случаем задачи поиска потока минимальной стоимости. В то же время частным случаем транс­портной задачи являются задачи о назначениях, например задача оптимального распределения по населенным пунктам торговых агентов или маркетологов для изучения рынка. Подробный разбор данной задачи мы провели на лекции 3 «Оптимальные решения в линейных задачах управления производством и цепями поставок».

 

СПИСОК  РЕКОМЕНДУЕМОЙ  ЛИТЕРАТУРЫ.

 

[1] Таха Х.А. Введение в исследование операций. — 6-е изд. Пер. с англ. — М.: Издательский дом «Вильямс», 2001. — 912 с: ил.

 

[2] Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

 [3] Шелобаев С. И. Математические методы и модели в экономике,  финансах, бизнесе: Учебное пособие для вузов. — М.: ЮНИТИ - ДАНА, 2001. - 367 с.

[4] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учебное пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).

 

[5] Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш,  Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.:  ЮНИТИ, 1999. - 391 с.