Методы оптимальных решений

 

Лекция 3

 

Тема лекции 3: «Оптимальные решения в линейных задачах управления производством и цепями поставок»

 

Разделы лекции:

 

1. Линейная задача планирования производства. Задача о расшивке узких мест производства.

2. Перевозка грузов. Транспортная задача.

3. Итерационный алгоритм решения  транспортной задачи. Метод потенциалов.

 

 

РАЗДЕЛ 1. ЛИНЕЙНАЯ ЗАДАЧА ПЛАНИРОВАНИЯ ПРОИЗВОДСТВА. ЗАДАЧА О РАСШИВКЕ УЗКИХ МЕСТ ПРОИЗВОДСТВА.

 

Мы уже неоднократно рассматривали задачу оптимального планирования производства. Теперь мы проведем подробное исследование конкретного примера такой задачи с использованием всей изученной теории.

 

ПРИМЕР 1. (ЗАДАЧА О ПЛАНИРОВАНИИ ВЫПУСКА ТКАНЕЙ).

 

Фабрика «Нить Ариадны» выпускает три вида тканей, при­чем суточное плановое задание составляет не менее 90 м тканей первого вида, 70 м — второго и 60 м — третьего.

 

Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии.

 

Расход указанных ресурсов на один метр ткани представлен в таблице 1.

 

Цена за один метр ткани вида I равна 80 денежным единицам, II — 70 денежным единицам, III — 60 денеж­ным единицам.

 

Таблица 1.

Ресурсы	Расход ресурсов (количество единиц ресурса на 1 метр ткани)
	Ткань I вида	Ткань II вида	Ткань III вида
Оборудование	2	3	4
Сырье	1	4	5
Электроэнергия	3	4	2
Цена за 1 метр ткани	80	70	60

 

 

Необходимо определить, сколько метров ткани каждого вида следует выпустить, чтобы общая стоимость выпускае­мой продукции была максимальной.

 

Составим модель задачи. Введем следующие обозначе­ния. Неизвестными в задаче являются объемы выпуска тка­ни каждого вида:

 

x1 – количество метров ткани вида I;

 

x2 – количество метров ткани вида II;

 

x3 – количество метров ткани вида III.

 

С учетом имеющихся данных модель примет вид:

 

 

В результате решения задачи симплексным методом получен следующий оптимальный план: максимум общей стоимости продукции f(X)= 19075 у.е. при

 

x1=112,5 м — оптимальный план выпуска ткани вида I;

 

x2=70 м — оптимальный план выпуска ткани вида II;

 

x3=86,25 м — оптимальный план выпуска ткани вида III.

 

 

Решение двойственной задачи получим с использованием теорем двойственности. Введем обозначения:

 

y1 – двойственная оценка ресурса «оборудование»;

 

y2 – двойственная оценка ресурса «сырье»;

 

y3 – двойственная оценка ресурса «электроэнергия»;

 

y4 – двойственная оценка ткани вида I;

 

y5 – двойственная оценка ткани вида II;

 

y6 – двойственная оценка ткани вида III.

 

Модель двойственной задачи имеет вид:

 

 

Из соотношений второй теоремы двойственности выте­кают следующие условия.

 

Для каждого ресурса имеем соотношения (*) :

 

 

Для задания по выпуску продукции имеем соотношения (**):

 

 

Для нашего примера в этих соотношениях m=3 (количе­ство типов ресурсов).

 

Подставим значения x1=112,5, x2=70 и x3=86,25 в ограничения прямой задачи:

 

 

Суточные ресурсы по оборудованию и электроэнергии ис­пользованы полностью. Сырье используется не полностью, имеется остаток в размере 850 — 823,75 = 26,25 (кг). План выпуска по тканям вида I и III перевыполнен. Из второй теоремы двойственности вытекает, что y2, y4 и y6 равны нулю. Остается найти значения у1, y3 и y5. Так как x1, x2 и x3 — больше нуля, то все три ограничения двойственной задачи выполняются как равенства:

 

Учитывая, что y2=y4=y6=0, имеем:

 

Откуда y1=2,5; у3=25; y5= -37,5.

 

Подставив значения неизвестных в целевую функцию двойственной задачи, проверим, выполняется ли условие f(X)=g(Y) для оптимального плана:

 

g(Y) =780∙2,5 + 850∙0+ 790∙25 + 90∙0 –70∙37,5 + 60∙0 = 19075.

 

 

Условие первой теоремы двойственности выполняется, сле­довательно, рассмотренный план выпуска тканей и соответст­вующая ему система оценок ресурсов и продукции оптимальны.

 

Перейдем к рассмотрению конкретных экономических свойств оценок yj оптимального плана.

 

Имеем следующие свойства двойственных оценок.

 

Свойство 1. Оценки как мера дефицитности ресурсов и продукции.

 

Свойство 2. Оценки как мера влияния ограничений на функционал.

 

Свойство 3. Оценки как инструмент определения эффективности отдельных вариантов.

 

Свойство 4. Оценки как инструмент балансирования суммарных затрат и результатов.

 

 

Экономическое истолкование оценок есть интерпретация их общих экономико-математических свойств применитель­но к конкретному содержанию задачи.

 

ДЕФИЦИТНОСТЬ РЕСУРСОВ.

 

По условию (*) не использованный полностью в оптимальном плане ресурс по­лучает нулевую оценку. Нулевая оценка ресурса свидетель­ствует о его недефицитности. Ресурс недефицитен не из-за его неограниченных запасов (они ограничены величиной bi), а из-за невозможности его полного использования в опти­мальном плане. Так как суммарный расход недефицитного ресурса меньше его общего количества, то план производст­ва им не лимитируется.  Данный ресурс не препятствует и дальше максимизировать целевую функцию f(X). Ограничивают целевую функцию дефицитные ресурсы, в данном примере — оборудование и электроэнергия. Они пол­ностью использованы в оптимальном плане. По условию (*) оценка таких ресурсов положительна (y1=2,5; y3=25).

 

 

ДЕФИЦИТНОСТЬ ПРОДУКЦИИ.

 

Рассмотрим теперь понятие дефицитности продукции. По условию (**) нулевую оценку (y4=y6=0) получает продукция, задания по выпуску которой в оптимальном плане перевыполняются. Очевидно, перевыполнение плана целесообразно по выгодной продукции (ткани I и III видов), т. е. такой, производство которой способствует достижению максимума критерия оптимальности. Размеры производства такой выгодной продукции определяются не величиной за­дания на выпуск (Tj) (в оптимальном плане они перекрыты), а ограниченностью дефицитных ресурсов. Эту продукцию выпускают как можно больше, пока хватит ресурсов. Выпуск выгодной продукции лимитируется не только фактом ограниченности дефицитных ресурсов, но и тем, что часть дефицитных ресурсов требуется выделить на обеспече­ние выпуска невыгодной продукции в соответствии с плано­выми заданиями.

 

По условию (**) отрицательную оценку (y5= –37,5) получает продукция, задания по выпуску которой не перевыполняются. Так как по условию задачи (xj≥Tj) плановые задания должны быть обязательно выполнены, то продукция делится на выгодную (виды I и III ткани) и не­выгодную (вид II ткани). Если в ограничение двойственной задачи, относящееся к виду II ткани:

 

3y1+4у2+4y3+y5≥70

 

подставить полученные значения двойственных оценок, то получаем:

3∙2,5+4∙0+4∙25 – 37,5 = 70.

 

Отсюда,  107,5 - 37,5=70, т. е. стоимость ресурсов, затраченных на один метр ткани вида II, составляет 107,5 денежных единиц и это на 37,5 денежных единиц больше цены одного метра ткани этого вида. Таким образом, вид II ткани убыточен для фабрики: на каждом выпущенном метре ткани этого вида фабрика теряет 37,5 денежных единиц.

 

 

В соответствии с критерием оптимальности плана, в за­висимости от того, перевыполняется план выпуска или нет, выпуск ткани вида II поглощает часть дефицитных ресур­сов, чем сдерживает рост выпуска выгодной продукции, а тем самым и рост целевой функции.

 

Оценка ресурса показывает, на сколько изменится крите­рий оптимальности при изменении количества данного ре­сурса на единицу. Для недефицитного ресурса оценка равна нулю, поэтому изменение его величины не повлияет на кри­терий оптимальности. Дефицитность ресурса измеряется вкладом единицы ресурса в изменение целевой функции.

 

Влияние ограничений по выпуску продукции на критерий оптимальности противоположно влиянию ограничений по ре­сурсам. Если продукция невыгодна (вид II ткани, y5= -37,5), то увеличение плановых заданий по ее выпуску ведет к уменьшению выпуска выгодной продукции и ухудшает план. Наоборот, уменьшение плановых заданий по невыгод­ной продукции позволяет снизить ее выпуск, перебросить сэкономленные ресурсы на дополнительный сверхплановый выпуск выгодных видов продукции, что увеличивает значение целевой функции. Изменение плановых заданий по выгодной продукции не изменяет значения целевой функции. После того как оптимальное решение получено, выявля­ется его чувствительность к определенным изменениям ис­ходной модели. В нашей задаче, например, может пред­ставить интерес то, как повлияет на оптимальное решение изменение запасов сырья и изменение прибыли от единицы продукции. В связи с этим логично выяснить:

 

1. Увеличение объемов какого вида ресурсов наиболее вы­годно?

 

2. На сколько можно увеличить запас сырья для улучшения полученного оптимального значения целевой функции?

 

3. Каков диапазон изменения того или иного коэффициен­та целевой функции, при котором не происходит изме­нения оптимального решения?

 

4. Целесообразность включения в план новых изделий.

 

ЦЕННОСТЬ РЕСУРСОВ.

 

В примере 1 были использованы следующие двойственные оценки: y1 – двойственная оценка ресурса «оборудование»; y2 – двойственная оценка ресурса «сырье»; y3 – двойственная оценка ресурса «электроэнергия».

 

В примере 1 двойственные оценки ресурсов y1=2,5 («оборудование»); y3=25 («электроэнергия») положительны (y1>0, y3>0).

Дефицитный ресурс, полностью используемый в оптималь­ном плане:

 

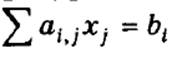
имеет положительную оценку (yj>0).

Недефицитный, не полностью используемый ресурс, для которого

 

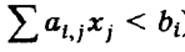
имеет нулевую оценку (yj=0).

 

 

 

В примере 1 «сырье» не является дефицитным ресурсом: y2=0, а «оборудование» и «электроэнергия» – дефицитные ресурсы: y1=2,5; y3=25.

 

 

Чем выше величина оценки yi, тем острее дефицитность i-гo ресурса.

 

В примере 1 ресурс «электроэнергия» более дефицитен, чем «оборудование»: y3=25>2,5=y1. Поэтому наиболее выгодно увеличение объемов ресурса «электроэнергия».

 

ЗАМЕЧАНИЕ. Заметим, что ценность различных видов сырья нельзя отождествлять с действительными ценами, по которым осу­ществляется его закупка. В данном случае речь идет о не­которой мере, имеющей экономическую природу, которая характеризует ценность сырья только относительно полу­ченного оптимального решения.

 

Более детально три  первые свойства двойственных оценок (оценки как меры дефицитности ресурсов, оценки как меры влияния ограничений на функционал, оценки как инструмент определения эффективности отдельных вариантов) и использование этих свойств при анализе оптимальных решений экономических задач рассмотрены в учебном пособии [5]. Свойство двойственных оценок как инструмента балансирования суммарных затрат и результатов — вытекает из первой теоремы двойственности, в которой устанавливается связь между функционалами прямой и двойственной задач: max f(X)=min g(Y). В конкретных задачах такого рода соотношения «затраты — результаты», т. е. равновесие затрат и результатов в точке оптимума, могут иметь различное экономическое содержание. В рассматриваемой нами задаче экономический смысл равенства функционалов прямой и двойственной задач состоит в том, что максимум прибыли может быть обеспечен лишь при минимуме недополученной прибыли от использования дефицитных ресурсов.

 

ЗАДАЧА О РАСШИВКЕ УЗКИХ  МЕСТ ПРОИЗВОДСТВА.

 

При выполнении оптимальной производственной программы может оказаться так, что некоторые ресурсы расходуются полностью. Говорят, что такие ресурсы образуют узкие места производства. Наличие узких мест в силу неустойчивости решения задач линейного программирования может привести к тому, что потеря достаточно малого количества некоторого ресурса, имеющего сравнительно низкую стоимость (относительно суммарной прибыли) может привести к тому, что оптимальное значение прибыли уменьшится намного сильнее, чем на стоимость потерянного ресурса.  Рассмотрим тривиальный пример.

 

ПРИМЕР 2. Предприятие собирает автомобили из готовых узлов и агрегатов. Для изготовления одного автомобиля требуется один кузов с подвеской (в сборе), один двигатель и четыре колеса. Производство одного автомобиля приносит предприятию чистую прибыль 50 тыс. руб. В наличии у предприятия имеется 2 кузова , 2 двигателя и 8 колес. Требуется определить, какие убытки принесет предприятию потеря (в результате хищения) одного колеса (стоимостью 2 тыс. руб.).

РЕШЕНИЕ.

 

Казалось бы, убытки предприятия равны 2 тыс. руб. Но это не так. Из 2 кузовов, 2 двигателей и 8 колес предприятие могло изготовить 2 автомобиля и получить прибыль 100 тыс. руб. После утраты колеса предприятие может собрать только 1 автомобиль и получить прибыль в 2 раза меньше — всего 50 тыс. руб.  

 

Конечно, недостающее колесо можно приобрести, но это требует времени, которое предприятию придется простаивать.  Итак, если колесо можно купить мгновенно, то убытки предприятия составляют 2 тыс. руб., если колесо купить вообще невозможно, то убытки предприятия составят 50 тыс. руб., а в общем случае убытки равны стоимости простоя предприятия в течение того времени, которое занимает закупка колеса.

 

Расшивка узких мест производства заключается в закупке дополнительных единиц тех ресурсов, которые полностью используются при выполнении оптимальной производственной программы. В общем случае расшивка узких мест производства позволяет максимально задействовать имеющийся потенциал предприятия по производству данной продукции по данным технологиям в условиях существующих цен.

 

РАЗДЕЛ 2. ПЕРЕВОЗКА ГРУЗОВ. ТРАНСПОРТНАЯ ЗАДАЧА.

 

Как показано выше, многие прикладные модели в эконо­мике сводятся к задачам линейного программирования. Практически все задачи линейного программирования можно решить, используя ту или иную модификацию симплексного метода. Однако существуют более эффективные вычислитель­ные процедуры решения некоторых типов задач линейного программирования, основанные на специфике ограничений этих задач.  Важный тип задач линейного программирования представляет задача о перевозках. Называется она так потому, что цель этой задачи заключается в минимизации полной стоимости перевозок известного количества товаров со складов к потребителю.

 

ОПРЕДЕЛЕНИЕ ТРАНСПОРТНОЙ МОДЕЛИ.  

 

Транспортные модели (задачи) - специальный класс задач линейного программирования. Эти модели часто описывают перемещение (перевозку) какого-либо товара из пункта отправления (исходный пункт, например место производства) в пункт назначения (склад, магазин, грузохранилище). Назначение транспортной задачи – определение объемов перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, накладываемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов в пунктах назначения (спрос). В транспортной модели предполагается, что стоимость перевозки по какому-либо маршруту прямо пропорциональна объему груза, перевозимого по этому маршруту. В общем случае транспортную модель можно применять для описания ситуаций, связанных с управлением запасами, управлением движением капиталов, составлением расписаний, назначением персонала и др.

Мы поговорим здесь о так называемой сбалансированной транспортной задаче — задаче о перевозках, в которой общий объем товаров, готовых к отправлению, в точности равен объему товаров, который готовы принять в пунктах назначения.

 

ПРИМЕР 1.  Компания имеет два товарных склада и трех оптовых покупателей. Известно, что общий объем запасов на складах составляет 300 тыс. единиц продукции и совпадает с общим объемом заказов покупателей.

Конкретные данные о загруженности каждого из складов (в тыс. ед.), потребности каждого покупателя (в тыс. ед.) и стоимости перевозки (млн. руб. за 1 тыс. ед.) приведены в следующей таблице (таблица1).

 

Таблица 1.

		Стоимость перевозок к потребителям (млн. руб. за 1 тыс. ед.)			Наличие (тыс. ед.)
		B1	B2	B3
Склады	А1	8	5	6	120
	А2	4	9	7	180
Запрос (тыс. ед.)		70	140	90	300

 

 

Обозначим через xij количество товара, поставляемого со склада Ai покупателю Bj (рисунок 1).

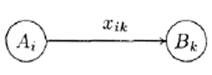
Рисунок 1.

Тогда соответствующая транспортная задача может быть сформулирована следующим образом. Минимизировать общую стоимость перевозок:

 

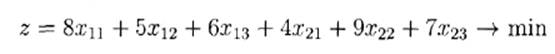
при условии, что:

 

 

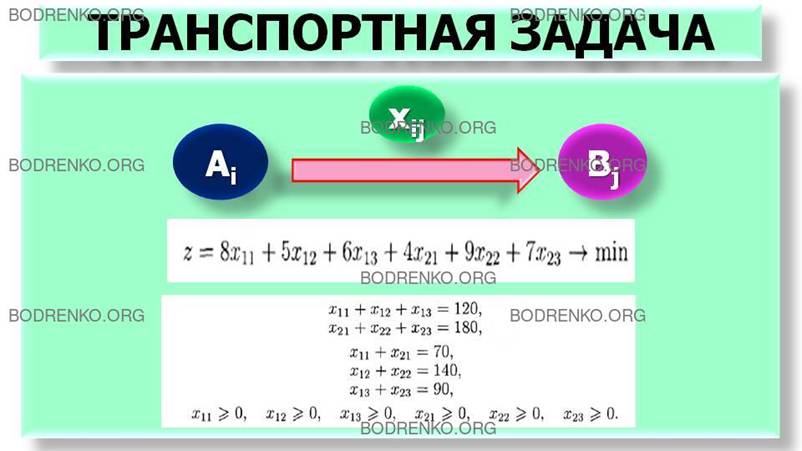
Получаем задачу линейного программирования, в которой основные ограничения вследствие того, что транспортная задача сбалансирована, являются равенствами.

 

ЗАМЕЧАНИЕ. Для лучшего понимания поставленной задачи часто полезно воспользоваться сетью (рисунок 2).

 

 

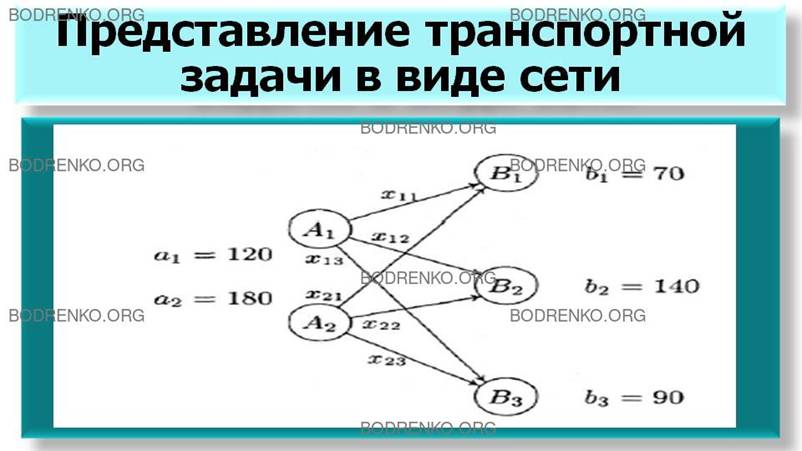
Рисунок 2. Представление транспортной задачи в виде сети.

 

Перейдем теперь к общей постановке сбалансированной транспортной задачи. Рассмотрим так называемую транспортную задачу по критерию стоимости, которую можно сформулировать следующим образом.

В m пунктах отправления А1, А2, ...,Аm, которые в даль­нейшем будем называть поставщиками, сосредоточено опре­деленное количество единиц некоторого однородного про­дукта, которое обозначим аi (i=1, 2, ..., m). Данный про­дукт потребляется в n пунктах В1,В2,… , Вn, которые будем называть потребителями; объем потребления обозначим bj (j = 1, 2, ..., n). Известны расходы на перевозку единицы продукта из пункта Ai в пункт Bj, которые равны cij и при­ведены в матрице транспортных расходов С=||cij||. Требуется составить такой план прикрепления потреби­телей к поставщикам, т.е. план перевозок, при котором весь продукт вывозится из пунктов Ai в пункты Bj в соответ­ствии с потребностью и общая величина транспортных из­держек будет минимальной.

Обозначим количество продукта, перевозимого из пункта Ai в пункт Bj, через xij.

 

Тогда общее количество товара, которое можно отправить из пункта Ai в пункты В1, В2, …, Вn, равно:

 

n

∑xij =ai.

j=1

 

Общее количество товара, которое можно принять в пункте Bj из пунктов А1, А2, ..., Аm, равно:

 

m

∑ xij =bj.

i=1

Стоимость перевозки хij единиц товара из пункта Аi в пункт Вj равна cij∙xij, а общая стоимость всех перевозок z равна:

m   n

∑   ∑ xij  .

 i=1  j=1

 

В результате мы получаем следующую задачу линейного программирования. Совокупность всех переменных xij для краткости обозначим X , тогда целевая функция задачи будет иметь вид:

  

           m   n

f(X) = ∑   ∑ xij  => min ,

         i=1  j=1

 

(1)

а ограничения выглядят следующим образом:

m

∑ xij =bj, (j=1, …, n)

i=1

(2)

n

∑xij =ai, (i=1, …, m)

j=1

(3)

 

xij≥ 0 (i=1, …, m, j=1, …, n).

 

Условия (2) означают полное удовлетворение спроса во всех пунктах потребления; условия (3) определяют полный вывоз продукции от всех поставщиков.

 

Необходимым и достаточным условием разрешимости задачи (1) – (3) является условие баланса:

m        n

∑ ai = ∑ bj.

i=1     j=1

 

(4)

 

 

Транспортная задача, в которой имеет место равенство (4), называется закрытой и может быть решена, как за­дача линейного программирования с помощью симплексного метода. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения.  

 

На рисунке 3 показано представление транспортной задачи в виде сети с m пунктами
отправления и n пунктами назначения, которые показаны в виде узлов сети. Дуги, соединяющие узлы сети, соответствуют маршрутам, связывающим пункты отправления и назначения. С дугой (i , j), соединяющей пункт отправления Ai с пунктом назначения Bj, соотносятся два вида данных: (1) стоимость cij перевозки единицы груза из пункта Ai в пункт Bj и (2) количество перевозимого груза хij. Объем грузов в пункте отправления Ai равен аi, а объем грузов в пункте назначенияBj равен bj. Задача состоит в определении неизвестных величин  xij, минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям, накладываемым на объемы грузов в пунктах отправления (предложения) и пунктах назначения (спрос).

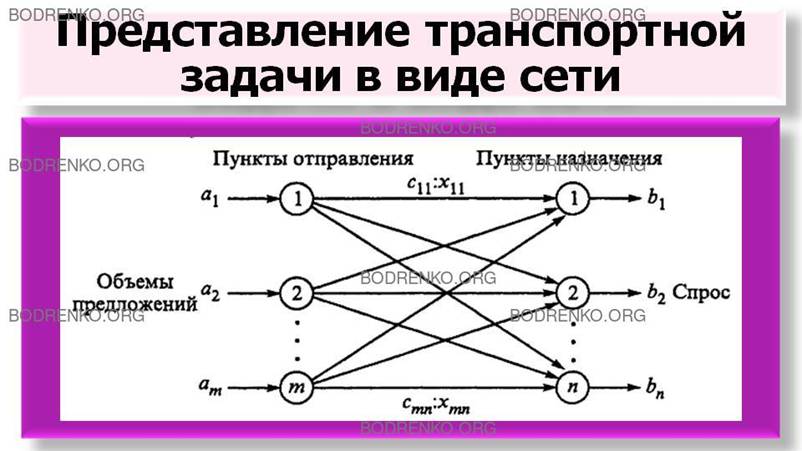
Рисунок 3. Представление транспортной задачи в виде сети.

 

РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ.  

 

В данном разделе будет детально описан алгоритм решения транспортной задачи. Этот алгоритм повторяет основные шаги симплекс-метода. Однако для представления данных, вместо обычных симплекс-таблиц, используются транспортные таблицы и со специальной структурой. Алгоритм решения транспортной задачи будет проиллюстрирован на следующем примере. 

 

ПРИМЕР 2. Транспортная компания «Кот в сапогах» занимается перевозкой зерна специальными зерновозами от трех элеваторов к четырем мельницам. В таблице 2 показаны возможности отгрузки зерна (предложения) элеваторами (в зерновозах) и потребности (спрос) мельниц (также в зерновозах), а также стоимость перевозки зерна одним зерновозом от элеваторов к мельницам. Стоимость перевозок cij приведена в сотнях долларов.

Таблица 2.

 

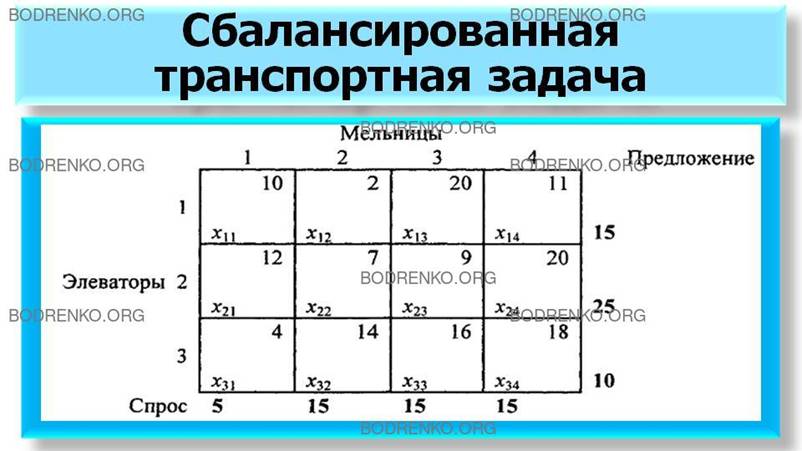
В данной задаче требуется определить структуру перевозок между элеваторами  и мельницами с минимальной стоимостью. Для этого необходимо найти объемы  перевозок хij между i-м элеватором и j-й мельницей.  Последовательность шагов алгоритма решения транспортной задачи в точности повторяет аналогичную последовательность этапов симплексного алгоритма.

 

ШАГ 1. Определяем начальное базисное допустимое решение, затем переходим к выполнению второго шага.

 

ШАГ 2. На основании условия оптимальности симплекс-метода среди всех небазисных переменных определяем переменную, вводимую в базис. Если все небазисные переменные удовлетворяют условию оптимальности, вычисления заканчиваются; в противном случае переходим к третьему шагу.

 

ШАГ 3.  С помощью условия допустимости симплекс-метода среди текущих базисных переменных определяем исключаемую переменную. Затем находим новое базисное решение. Возвращаемся ко второму шагу.  

 

Рассмотрим каждый описанный шаг в отдельности. 

 

ШАГ 1. ОПРЕДЕЛЕНИЕ НАЧАЛЬНОГО РЕШЕНИЯ.

 
Общая транспортная модель с m пунктами отправления и n пунктами назначения имеет (m+n) ограничений в виде равенств, по одному на каждый пункт отправления и назначения. Поскольку мы рассматриваем сбалансированную транспортную модель (сумма предложений = сумме спроса), одно из этих равенств должно быть избыточным. Таким образом, транспортная модель имеет (m+n–1) независимых ограничений, отсюда вытекает, что начальное базисное решение состоит из (m+n–1) базисных переменных. Например, начальное решение в примере 2 содержит (3+4–1=6) базисных переменных.
Специальная структура транспортной модели для построения начального решения позволяет применить следующие методы (вместо использования искусственных переменных, как это делается в симплекс-методе).

 

1 . Метод северо-западного угла. 

 

2. Метод наименьшей стоимости. 

3. Метод Фогеля. 

 

Различие этих методов заключается в «качестве» начального решения, т.е. насколько начальное решение ближе к оптимальному. В общем случае метод Фогеля дает наилучшее решение, а метод северо-западного угла наихудшее. Однако метод северо-западного угла требует меньшего объема вычислений.

 

МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА. Выполнение начинается с верхней левой ячейки (северо-западного угла) транспортной таблицы, т.е. с переменной х11.

 

Шаг 1. Переменной х11 присваивается максимальное значение, допускаемое ограничениями на спрос и предложение.

 

Шаг 2. Вычеркивается строка (или столбец) с полностью реализованным предложением (с удовлетворенным спросом). Это означает, что в вычеркну той строке (столбце) мы не будем присваивать значения остальным переменным (кроме переменной, определенной на первом шаге). Если одновременно удовлетворяются спрос и предложение, вычеркивается только строка или только столбец.

 

Шаг З. Если не вычеркнута только одна строка или только один столбец, процесс останавливается. В противном случае переходим к ячейке справа, если вычеркнут столбец, или к нижележащей ячейке, если вычеркнута строка. Затем возвращаемся к первому шагу.

Если применить описанную процедуру к задаче из примера 2, получим начальное базисное решение, показанное в таблице 3. В этой таблице стрелками показана последовательность определения базисных переменных. 

Таблица 3.

 

Получено следующее начальное базисное решение: x11=5, x12=10,x22=5, x23=15, x24=5, x34=10.

Соответствующая суммарная стоимость перевозок равна:

z=5∙10+ 10∙2+5∙7+ 15∙9 + 5∙20+ 10∙18=$520.

МЕТОД НАИМЕНЬШЕЙ СТОИМОСТИ.

Данный метод находит лучшее начальное решение, чем метод северо-западного угла, поскольку выбирает переменные, которым соответствуют наименьшие стоимости. Сначала по всей транспортной таблице ведется поиск ячейки с наименьшей стоимостью. Затем переменной в этой ячейке присваивается наибольшее значение, допускаемое ограничениями на спрос и предложение. (Если таких переменных несколько, выбор произволен.) Далее вычеркивается соответствующий столбец или строка и соответствующим образом корректируются значения спроса и предложений. Если одновременно выполняются ограничения и по спросу, и по предложению, вычеркивается или строка, или столбец (точно так же, как в методе северо-западного угла). Затем просматриваются не вычеркнутые ячейки, и выбирается новая ячейка с минимальной стоимостью. Описанный процесс продолжается до тех пор, пока не останется лишь одна не вычеркнутая строка или столбец.

ЗАМЕЧАНИЕ. Этот метод в русской математической литературе часто называют методом минимального элемента.

 

Применим метод наименьшей стоимости к задаче из примера 2.

1. Ячейка (1,2) имеет наименьшую в таблице стоимость (=$2). Наибольшее значение, которое можно присвоить переменной х12, равно 15. В этом случае удовлетворяются ограничения, соответствующие первой строке и второму столбцу. Вычеркиваем второй столбец, предложение первой строки и спрос второго столбца принимают нулевые значения.

2. Следующей ячейкой с наименьшей стоимостью в незачеркнутой части таблицы будет ячейка (3,1) – стоимость перевозки единицы груза равна $4. Присвоим переменной х31 значение 5 и вычеркнем первый столбец. Ограничение по предложению, соответствующее третьей строке, станет равным: 10–5=5.  

 

3. Продолжая процедуру, последовательно присваиваем переменной х23 значение 15, переменной х14=0 – значение 0; далее находим х34=5 и х24=10.
Процесс поиска начального решения представлен в таблице 4. Стрелками показана последовательность присвоения переменным значений.

 

Таблица 4.

 

 

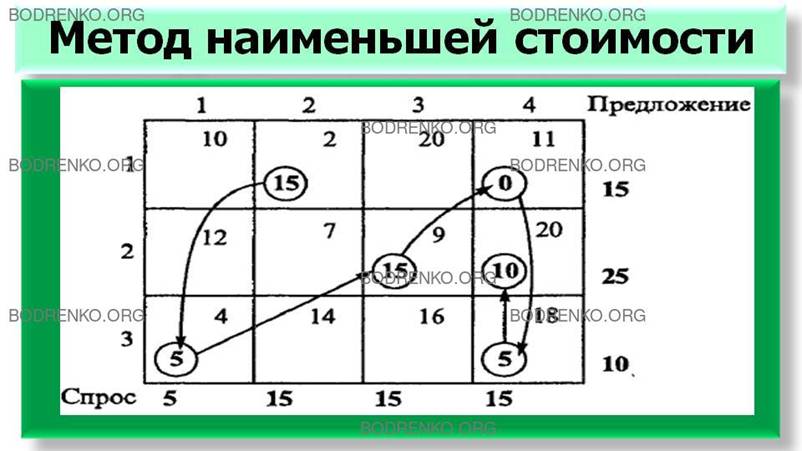
Итак, получили следующее начальное базисное решение (состоящее из 6 переменных):  х12=15, х14=0, х23=15, х24=10, х31=5, х34=5.

 

Соответствующее значение целевой функции равно:

 

z=15∙2+0∙11+15∙9+10∙20+5∙4+5∙18=$475.

 

Отсюда следует, что полученное методом наименьшей стоимости начальное решение лучше, чем начальное решение, представленное методом северо-западного угла (сравните данное значение целевой функции с аналогичным значением из примера 2, вычисленным по методу северо-западного угла).

 
МЕТОД ФОГЕЛЯ. Данный метод является вариацией метода наименьшей стоимости и в общем случае находит лучшее начальное решение. Алгоритм этого метода состоит из следующих шагов.

 

ШАГ 1. Для каждой строки (столбца), которой соответствует строго положительное предложение (спрос), вычисляется штраф путем вычитания  наименьшей стоимости из следующей по величине в данной строке.

 

ШАГ 2. Выделяется строка или столбец с наибольшим штрафом. Если таковых несколько, выбор произволен. Из выделенной строки или столбца выбирается переменная, которой соответствует минимальная стоимость, и ей присваивается наибольшее значение, позволяемое ограничениями. Затем в соответствии с присвоенным значением переменной корректируются величины оставшегося неудовлетворенным спроса и нереализованного предложения. Строка или столбец, соответствующие выполненному ограничению, вычеркиваются из таблицы. Если одновременно выполняются ограничения и по спросу, и по предложению, вычеркивается только строка или только столбец, причем оставшейся строке (столбцу) приписывается нулевое предложение (спрос).

 

ШАГ 3.  

 

(а) Если не вычеркнута только одна строка или только один столбец с нулевым спросом или предложением, вычисления заканчиваются.  

 

(b) Если не вычеркнута только одна строка (столбец) с положительным предложением (спросом), в этой строке (столбце) методом наименьшей стоимости находятся базисные переменные, и вычисления заканчиваются.

 

(c) Если всем невычеркнутым строкам и столбцам соответствуют нулевые объемы предложения и спроса, методом наименьшей стоимости находятся нулевые базисные переменные, и вычисления заканчиваются. 

 

(d)  Во всех остальных случаях необходимо перейти к шагу 1.

Применим метод Фогеля к задаче из примера 2. В таблице 5 показан первый набор вычисленных штрафов.

 

Таблица 5.

 

 

Поскольку третья строка имеет наибольший штраф (10) и в этой строке наименьшая стоимость содержится в ячейке (3, 1), присваиваем переменной х31 значение 5. В этом случае полностью выполняется ограничение первого столбца, его вычеркиваем. Новый набор пересчитанных штрафов показан в таблице 6.

 

Таблица 6.

 

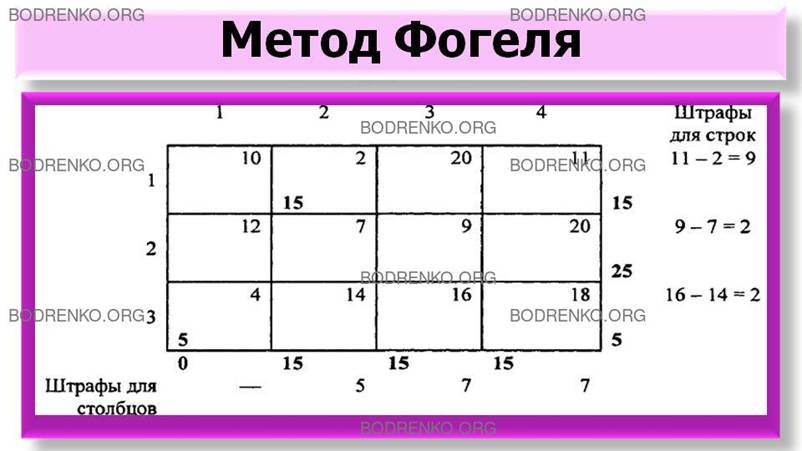
Теперь первая строка имеет наибольший штраф (9). Поэтому мы присваиваем значение 15 переменной х12, которой соответствует минимальная стоимость в первой строке. В этом случае одновременно выполняются ограничения и для первой строки, и для второго столбца. Вычеркнем второй столбец, положив объем предложений, соответствующий первой строке, равным нулю.  Продолжая этот процесс, находим, что на следующем шаге вторая строка будет иметь наибольший штраф (20 – 9=11). Поэтому переменной х23 присваиваем значение 15. В результате, будет вычеркнут третий столбец, во второй строке останется нереализованным предложение объемом в 10 единиц. Остается невычеркнутым только четвертый столбец с положительным неудовлетворенным объемом в 15 единиц. Применяя метод наименьшей стоимости к этому столбцу, последовательно получаем:  х14=0, x34=5, х24=10. Соответствующее значение целевой функции равно:

 

z=15∙2+0∙11+15∙9+10∙20+5∙4+5∙18=$475.

В данном случае значение целевой функции такое же, как и при методе наименьшей стоимости. Но обычно метод Фогеля дает наилучшее начальное решение для транспортной задачи.

РАЗДЕЛ 3. ИТЕРАЦИОННЫЙ АЛГОРИТМ РЕШЕНИЯ  ТРАНСПОРТНОЙ ЗАДАЧИ. МЕТОД ПОТЕНЦИАЛОВ.

 
После определения начального решения (с помощью одного из трех методов, описанных в предыдущем разделе) применяется алгоритм, позволяющий найти оптимальное решение транспортной задачи.

 

ШАГ 1. На основе симплексного условия оптимальности среди текущего множества небазисных переменных определяется вводимая в базис переменная, которая может улучшить значение целевой функции. Если условие оптимальности выполняется для всех небазисных переменных, вычисления заканчиваются, в противном случае необходимо перейти ко второму шагу.

 

ШАГ 2.  С помощью симплексного условия допустимости определяется исключаемая из базиса переменная. Происходит изменение базиса и возврат к первому шагу.

 

При изменении базиса в данном случае не используются вычисления, выполняемые при реализации симплекс-метода,  так как специальная структура транспортной таблицы позволяет значительно упростить вычисления.

 

ПРИМЕР 2 (ПРОДОЛЖЕНИЕ). Решим транспортную задачу из примера 2, используя начальное решение (таблица 3), полученное методом северо-западного угла в примере 2. Имеем следующее начальное решение: x11=5, x12=10,x22=5, x23=15, x24=5, x34=10.

 

 

Определение вводимой переменной среди текущих небазисных (т.е. среди тех переменных, которые не входят в начальное базисное решение) основано на вычислении коэффициентов z-строки, соответствующих небазисным переменным, с использованием метода потенциалов.   Метод потенциалов основан на соотношениях двойственности задачи ЛП.  В методе потенциалов каждой строке i и каждому столбцу j транспортной таблицы ставятся в соответствие числа (потенциалы) ui  и vj.  Для каждой базисной переменной хij потенциалы ui  и vj удовлетворяют уравнению: ui+vj=cij.

 

В рассматриваемой задаче имеем 7 неизвестных переменных (потенциалов) и 6 уравнений, соответствующих шести базисным переменным. Чтобы найти значения потенциалов из этой системы уравнений, нужно присвоить одному из них произвольное значение (обычно полагают u1=0) и затем последовательно вычислять значения остальных потенциалов.

 

 

Итак, имеем: u1=0, u2=5, u3=3; v1=10, v2=2, v3=4, v4=15.

 

Далее, используя вычисленные значения потенциалов, для каждой небазисной переменной вычисляются величины:  иi+vj – cij. Результаты вычисления этих величин приведены в следующей таблице.

Таблица 7.

 

 

Вычисленные значения совместно с нулевыми значениями для базисных переменных (поскольку (ui+vj – cij=0)  для любой базисной переменной xij) фактически являются коэффициентами z-строки симплекс-таблицы.

 

Поскольку в транспортной задаче ведется поиск минимума стоимости перевозок, вводимой в базис, будет переменная, имеющая наибольший положительный коэффициент в z-строке. В данном случае вводимой переменной будет х31.   Описанные вычисления обычно выполняются непосредственно в транспортной таблице, как показано в таблице 8. В этом случае нет необходимости в явном виде выписывать уравнения для потенциалов. Вычисления в транспортной таблице начинаются с присвоения потенциалу u1 нулевого значения: и1 =0. Затем вычисляются v-потенциалы для всех столбцов, имеющих базисные переменные в первой строке. Далее,  на основании уравнения для потенциалов, соответствующего переменной х22, вычисляется величина потенциала и2. Зная значение потенциала u2, вычисляем потенциалы v3 и v4, что позволяет найти потенциал u3. Поскольку все потенциалы определены, далее вычисляются величины:  иi +vj – cij для каждой небазисной переменной xij.  Эти величины показаны в таблице 8 в левом нижнем углу ячеек транспортной таблицы.

Таблица 8.

 

 

Определив вводимую в базис переменную х31, далее следует определить исключаемую из базиса переменную. Напомним, если какая-либо переменная вводится в базис, одна из текущих базисных переменных должна стать небазисной (и равной нулю), чтобы количество базисных переменных оставалось постоянным (в данном примере количество базисных переменных равняется 3+4–1=6).   Исключаемая из базиса переменная определяется следующим образом. Выбрав в качестве вводимой, переменную х31, мы хотим, чтобы перевозки по маршруту, соответствующему этой переменной, уменьшили общую стоимость перевозок. Какой объем груза можно перевести по этому маршруту? Обозначим через λ количество груза, перевозимого по маршруту (3,1) (т.е. х31=λ). Максимально возможное значение λ определяем из следующих условий.  

 

1. Должны выполняться ограничения на спрос и предложение.

 

2. Ни по какому маршруту не должны выполняться перевозки с отрицательным объемом грузов.

Эти условия позволяют найти значение λ и определить исключаемую переменную. Сначала построим замкнутый цикл, который начинается и заканчивается в ячейке, соответствующей вводимой переменной (в данном примере - это ячейка (3,1)). Цикл состоит из последовательности горизонтальных и вертикальных отрезков (но не диагональных), соединяющих ячейки, соответствующие текущим базисным переменным, и ячейку, соответствующую вводимой переменной. В таблице 9 показан цикл для вводимой переменной х31. Для любой вводимой переменной можно построить только один замкнутый цикл.

Таблица 9.

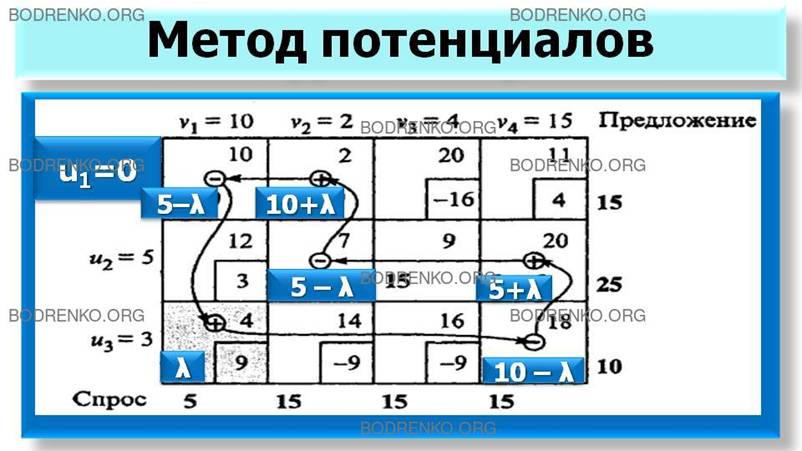
Теперь найдем значение λ. Для того чтобы удовлетворить ограничениям по спросу и предложению, надо поочередно отнимать и прибавлять λ к значениям базисных переменных, расположенных в угловых ячейках цикла, как показано в таблице 9 (не имеет значения направление обхода цикла: по часовой стрелке или против). Новые значения базисных переменных останутся неотрицательными, если будут выполняться следующие неравенства.

 
x11=5–λ≥0, x22=5–λ≥0, x34=10 –λ≥0.

 

Отсюда следует, что наибольшее значение, которое может принять λ, равно 5, при этом переменные x11 и х22 обращаются в нуль. Поскольку только одна переменная исключается из базиса, в качестве исключаемой переменной можно выбрать как х11, так и х22. Остановим свой выбор на х11.  Определив значение для вводимой переменной (x31=5) и выбрав исключаемую переменную, далее следует откорректировать значения базисных переменных, соответствующих угловым ячейкам замкнутого цикла, как показано в таблице 9. Поскольку перевозка единицы груза по маршруту (3,1) уменьшает общую стоимость перевозок на $9 (= u3+v1– c31), суммарная стоимость перевозок будет на $9∙5 =$45 меньше, чем в предыдущем решении.

 

Таким образом, новая суммарная стоимость перевозок будет равна $520– $45=$475.

 

Имея новое базисное решение, следует повторить вычисления потенциалов, как показано в таблице 10. Новой вводимой в базис переменной будет х14. Замкнутый цикл, соответствующий этой переменной, позволяет найти ее значение (х14=10) и исключаемую переменную х24.   Новое решение, показанное в таблице 10,  на $4∙10= $40 уменьшает значение целевой  функции. Таким образом, новая суммарная стоимость перевозок составляет $475–$40=$435.  Теперь новые значения величин (иi+vj – cij) для всех небазисных переменных xij отрицательные. Поэтому решение, представленное в таблице 10, оптимально.

Таблица 10.

 

 

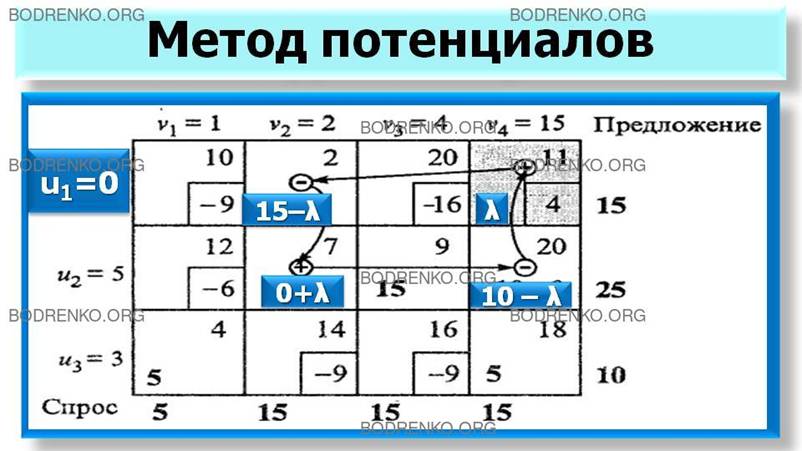
Полученное решение, в терминах исходной задачи перевозки зерна от элеваторов до мельниц, имеет следующий смысл.

 

Минимальная стоимость всех перевозок равна $435.

ЗАКЛЮЧЕНИЕ. Транспортная задача представляет собой частный случай общей задачи линейного программирования, специфическая структура которой позволяет разработать эффективные вычислительные методы, основанные на теории двойственности. Частными случаями транспортной задачи являются задача о назначениях и транспортная задача с промежуточными пунктами. Транспортная модель используется для описания проблем, не связанных с транспортировкой, например в задачах управления запасами и задачах производственного планирования.  Транспортные модели составляют один подкласс обобщенных сетевых моделей, которые мы рассмотрим в лекции 6. Некоторые последние обзоры показывают, что более 70% практических моделей линейного программирования можно рассматривать как сетевые, либо как модели, связанные с сетевыми.

СПИСОК  РЕКОМЕНДУЕМОЙ  ЛИТЕРАТУРЫ.

 

[1] Абчук В.А. Экономико-математические методы: Элементарная математика и логика. Методы исследования операций. СПб.: Союз, 1999. — 320 с.

 

[2] Таха Х.А. Введение в исследование операций. — 6-е изд. Пер. с англ. — М.: Издательский дом «Вильямс», 2001. — 912 с: ил.

[3] Шелобаев С. И. Математические методы и модели в экономике,  финансах, бизнесе: Учебное пособие для вузов. — М.: ЮНИТИ - ДАНА, 2001. - 367 с.

[4] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учебное пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).

 

[5] Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш,  Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.:  ЮНИТИ, 1999. - 391 с.