Математические методы исследования экономики

 

Лекция 9

 

Тема лекции 9: «Задачи оптимизации производства»

Разделы лекции:

 

1. Функции спроса на факторы (ресурсы).

2. Комбинация ресурсов (факторов производства), максимизирующая объем выпуска при ограничении на затраты.

3. Комбинация ресурсов (факторов производства), минимизирующая издержки при фиксированном (общем) объеме выпуска.

РАЗДЕЛ 1. ФУНКЦИИ СПРОСА НА ФАКТОРЫ (РЕСУРСЫ).

 

ОСНОВНЫЕ ПОНЯТИЯ.

Доходом (выручкой) R фирмы в определенном временном  периоде (например, в определённом году) называется произведение р0∙у общего объема у выпускаемой фирмой продукции на (рыночную) цену p0, этой продукции.

Издержками С фирмы называют общие выплаты фирмы в  определённом временном периоде за все виды затрат С = p1∙x1+ р2∙x2, где x1 и x2 - объемы затрачиваемых (используемых) фирмой ресурсов (факторов производства), p1 и р2- рыночные цены на эти ресурсы (факторы производства).

Прибылью PR фирмы в определённом временном периоде  называется разность между полученным фирмой доходом R и ее  издержками C производства: PR= R- С, или

PR(x1,x2) = р0∙f(x1,x2)  - (p1∙x1+ р2∙x2).

Последнее равенство есть выражение прибыли фирмы в  терминах затрачиваемых (используемых) ресурсов. Напомним, что у =f(x1,x2) - производственная функция фирмы, которая выражает  общий объем у выпускаемой фирмой продукции через объемы х1 и х2 затрачиваемых (используемых) ресурсов.

В теории фирмы принято считать,, что если фирма  функционирует в условиях чистой (совершенной) конкуренции, на рыночные цены p0, p1, p2 она влиять не может. Фирма «соглашается» с ценами p0, p1, и p2. Случаи функционирования фирмы в условиях чистой монополии, монополистической конкуренции и олигополии  специально рассматриваются в рамках курса по микроэкономике.

Основная цель фирмы заключается в максимизации прибыли  путем рационального распределения затрачиваемых (используемых) ресурсов. Формально задача максимизации прибыли в определённом временном периоде имеет вид:

 

PR => max.

 

Такая постановка задачи максимизации зависит от того, какой конкретно временной  промежуток (долговременный или краткосрочный) предшествует  периоду, в котором фирма максимизирует свою прибыль. В случае долговременного промежутка фирма может свободно выбирать любой вектор х = (х1, х2) затрат из пространства затрат (формально из неотрицательного ортанта х1≥0, x2≥0 плоскости Ох1х2. Поэтому задача максимизации прибыли в случае  долговременного временного промежутка имеет следующий вид:

р0∙f(x1,x2)  - (p1∙x1+ р2∙x2) = PR(x1,x2) => max ,

при условии, что

х1≥0, x2≥0

(постановка задачи в терминах затрачиваемых (используемых) ресурсов).

В случае краткосрочного промежутка фирма должна учитывать неизбежные лимиты на объемы затрачиваемых (используемых) ею ресурсов, которые формально могут быть записаны в виде  нелинейного, вообще говоря, неравенства

g(x1,x2)≤b

(ограничений вида  g(x1,x2)≤b может быть несколько).

Следовательно, задача максимизации прибыли для краткосрочного  промежутка имеет вид задачи математического программирования:

р0∙f(x1,x2)  - (p1∙x1+ р2∙x2) = PR(x1,x2) => max ,

при условии, что

g(x1,x2)≤b,

 х1≥0,

 

x2≥0.

 

(постановка задачи в терминах затрачиваемых (используемых) ресурсов).

ЧТО ТАКОЕ ИЗОКОСТА?

 

Линия уровня функции Z = p1∙x1+ р2∙x2 издержек производства называется изокостой (см. рисунок 1).

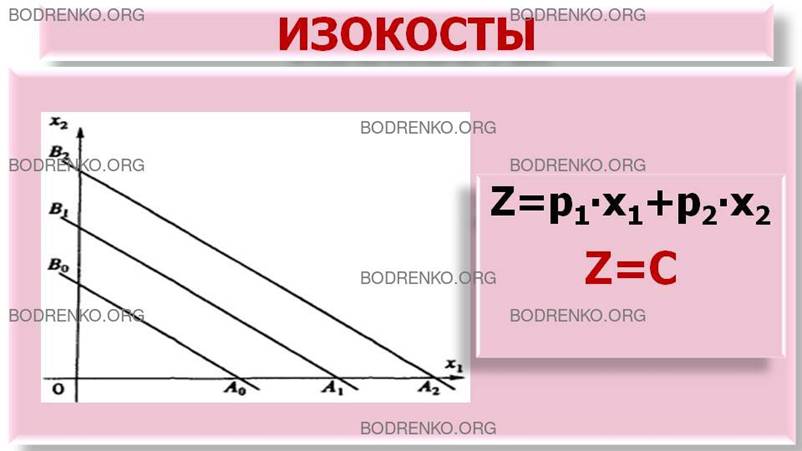
Рисунок 1. Изокосты.

 

В связи с тем, что по экономическому смыслу х1≥0, x2≥0  (так как х1 и x2 - это объемы затрачиваемых (используемых) ресурсов), строго говоря, изокоста есть отрезок прямой, попадающий в  неотрицательный ортант плоскости Ох1х2. Таким образом изокосты – это отрезки A0B0, A1B1, A2B2, …(см. рисунок 1). Отрезки A0B0, A1B1, A2B2 параллельны. Отрезок A1B1, расположенный «северо-восточнее»  отрезка А0В0, соответствует большим издержкам производства. Следовательно, если для отрезка A2B2 издержки производства С равны величине С2, т.е. С=С2, для отрезка A1B1 издержки производства С равны величине С1, т.е. С=С1, для отрезка для отрезка A0B0 издержки производства С равны величине С0, т.е. С=С0, то С0<С1<C2.

 

Верно и обратное, т.е. если С0<С1<C2, то отрезок А2В2, соответствующий издержкам производства С2, расположен «северо-восточнее» параллельного ему отрезка A1B1, соответствующего  издержкам производства С1. Аналогично, отрезок A1B1 расположен  «северо-восточнее» параллельного ему отрезка А0В0, соответствующего издержкам производства С0.

 

Для отрезка А0В0 имеем следующее  аналитическое представление:

С0 = p1∙x1+ р2∙x2,  х1≥0,  x2≥0.

 

Для отрезка A1B1:

С1 = p1∙x1+ р2∙x2,  х1≥0,  x2≥0.

 

для отрезка А2B2:

 С2 = p1∙x1+ р2∙x2,  х1≥0,  x2≥0.

 

ФУНКЦИИ СПРОСА НА ФАКТОРЫ (РЕСУРСЫ) В СЛУЧАЕ ДОЛГОВРЕМЕННОГО ПРОМЕЖУТКА.

В связи с тем, что, как правило, f(x1,0) = f(0,x2)=0 (т.е. если хотя бы один ресурс не затрачивается (не используется), то объем  выпускаемой продукции равен нулю), экономически осмысленными  являются векторы (x1, x2) затрат ресурсов, для которых х1>0,  x2>0. Поэтому в случае долговременного промежутка задача максимизации  прибыли представляет собой обычную задачу на глобальный  абсолютный максимум при х1>0,  x2>0. Из математического анализа  известно, что точки локального абсолютного максимума следует искать только среди точек (x1,x2), которые удовлетворяют системе уравнений:

∂PR(x1,x2)/∂x1=0, ∂PR(x1,x2)/∂x1=0.

 

Запишем эту систему дифференциальных уравнений в развернутом виде, вычислив левые части равенств (ибо прибыль PR(x1,x2) = р0∙f(x1,x2)  - (p1∙x1+ р2∙x2)).

 

Мы имеем:

 

р0∙∂f(x1,x2)/∂x1=p1,   р0∙∂f(x1,x2)/∂x2=p2.   (1)

 

Если вторые частные производные производственной функции таковы, что

∂2f(x1,x2)/∂x1∂x1<0, (∂2f(x1,x2)/∂x1∂x1)∙(∂2f(x1,x2)/∂x2∂x2)– (∂2f(x1,x2)/∂x1∂x2)²>0,

 

(эти неравенства несколько сильнее условий 2″ и 3 свойств производственных функций лекции 8, посвященной производственным функциям), то график производственной функции f(x1,x2) в трехмерном пространстве Оx1x2y есть поверхность, выпуклая вверх. Следовательно, график функции прибыли PR(x1,x2), получаемый путем вычитания из графика функции  р0∙f(x1,x2)  плоскости у =p1∙x1+ р2∙x2, являющейся графиком функции издержек производства, имеет вид «шапочки»,  у которой есть «макушка». «Макушка» соответствует глобальному максимуму прибыли:

PR(x1,x2) = р0∙f(x1,x2)  - (p1∙x1+ р2∙x2).

Из этого геометрического факта следует, что система (1) имеет единственное решение (х01,x02), которое является точкой не только локального, но и глобального (искомого нами) максимума прибыли PR(x1,x2).

 

ЧТО ТАКОЕ ЛОКАЛЬНОЕ (ЧАСТИЧНОЕ) РЫНОЧНОЕ РАВНОВЕСИЕ ФИРМЫ?

 

Вектор (х01,x02) затрат ресурсов, который является решением задачи максимизации прибыли

PR(x1,x2) = р0∙f(x1,x2)  - (p1∙x1+ р2∙x2), называется локальным (частичным) рыночным равновесием  фирмы (в случае долговременного промежутка).

Рисунок графика функции прибыли PR(x1,x2) в трехмерном пространстве, вообще говоря, достаточно сложен. Поэтому график функции прибыли представим схематически на плоскости Ozy, где координатная ось Oz изображает плоскость Ох1х2. На рисунке 2 даны графики производственной функции f(z), дохода фирмы р0∙f(z)  и издержек  производства p∙z.

 

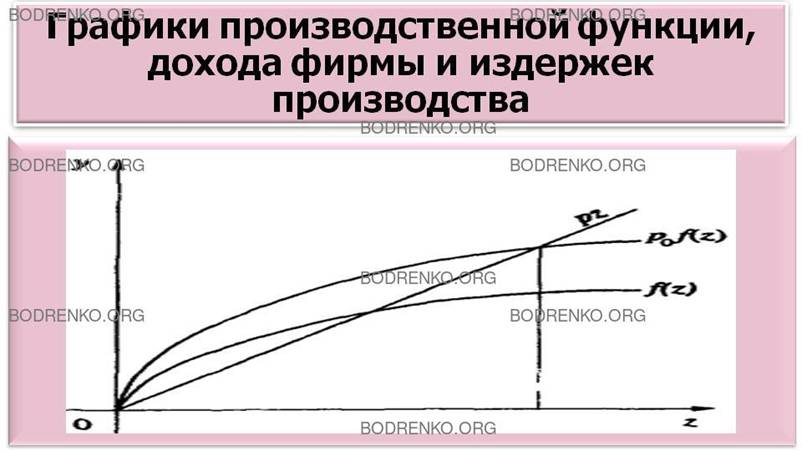
Рисунок 2. Графики производственной функции, дохода фирмы и издержек  производства.

 

 

 

На рисунке 3 изображен график функции прибыли PR(z) = р0∙f(z) - p∙z, который получен вычитанием из графика дохода фирмы р0∙f(z) графика функции издержек производства p∙z.  

 

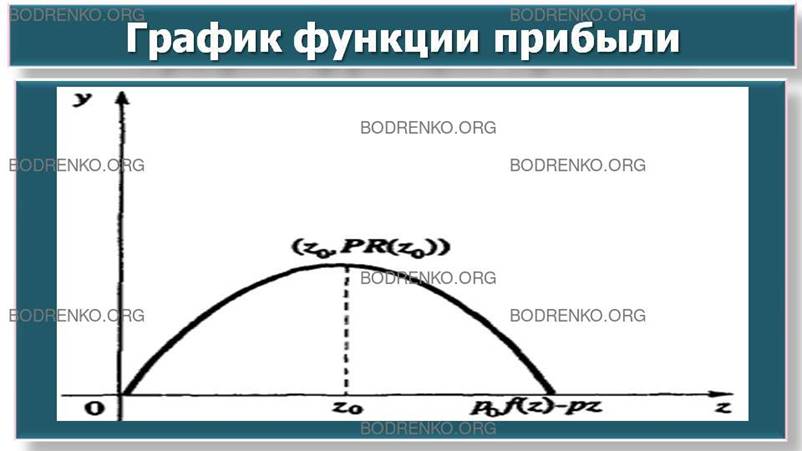
Рисунок 3. График функции прибыли.

 

Точка (z0, PR(z0)) есть «макушка» «шапочки» - графика функции PR(z) = р0∙f(z) - p∙z.

 

Подставив вектор (х01,x02) в уравнения (1), получим тождества:

р0∙∂f(x01,x02)/∂x1≡p1,   р0∙∂f(x01,x02)/∂x2≡p2.   (2)

 

Из (2) путем почленного деления первого тождества на второе получаем

(∂f(x01,x02)/∂x1)/(∂f(x01,x02)/∂x2)=p1/p2. (3)

То есть в точке (х01,x02)  локального рыночного равновесия фирмы отношение предельной производительности первого ресурса к  предельной производительности второго ресурса равно отношению  рыночных цен на эти ресурсы.

Проведем через точку (х01,x02)  изокванту и изокосту, которые эту точку содержат. Уравнение изокванты имеет вид:

 

f(x1,x2) =y0,

где у0=f(x01,x02).

 

Уравнение изокосты имеет вид:

 

 p1∙x1+ р2∙x2 =C0, где

С0 = p1∙x01+ р2∙x02 . (*)

Перепишем уравнение f(x1,x2) =y0,  выразив явно переменную x2 через переменную х1, т.е. в виде: x2=h(x1) (обратим внимание, что уравнения f(x1,x2) =y0 и x2=h(x1) формально разные, но они аналитически описывают одну и ту же изокванту (см. рисунок 4), где выполняется условие:

 

tg φ = -(dh(x01))/(dx1) = (∂f(x01,x02)/∂x1)/(∂f(x01,x02)/∂x2). (4)

 

 

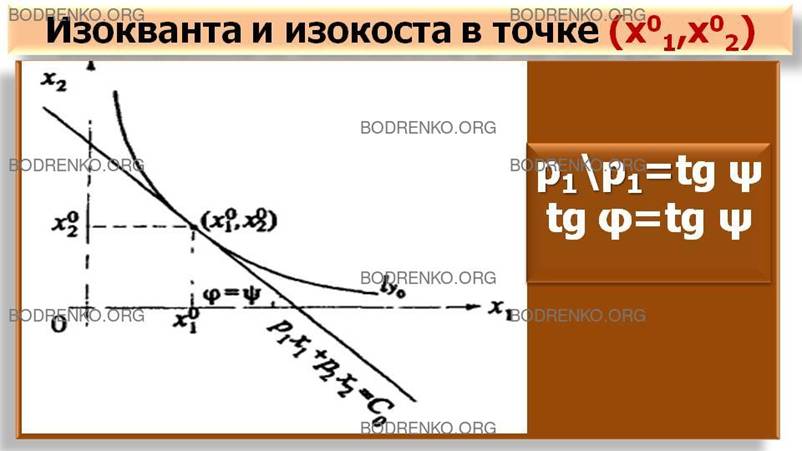
Рисунок 4. Изокванта и изокоста в точке (x01, x02).

 

Из математического анализа известно, что для изокосты, заданной уравнением  p1∙x1+ р2∙x2 =C0,  отношение p1/p2=tg ψ.

 

Из (3), (4) и (5) следует, что tg φ = tg ψ , что означает, что касательная K к изокванте ly0 в точке (х01, x02)  совпадает с изокостой, т.е. в точке (х01, х02) изокванта ly0 обязательно  касается изокосты K (см. рисунок 4).

 

ВЫВОД. Получена важная  геометрическая характеристика локального рыночного  равновесия (х01,x02) фирмы - касание в этом равновесии изокванты и изокосты.

Отметим, что, приступая к решению задачи максимизации  прибыли, мы не имели конкретных изокванты и изокосты, которые касаются друг друга в точке (х01,x02), так как не имели самой этой точки. Касающиеся друг друга изокванта и изокоста появляются после того, как аналитически найдено локальное рыночное  равновесие (х01,х02) путем решения системы уравнений (1).

Записанная в левой части уравнения (3) «четырехэтажная»  дробь  есть не что иное, как R12(x01,x02) - предельная норма замены первого ресурса вторым в точке (x01, x02).

ЗАМЕЧАНИЕ. Равенство (3) выражает следующий фундаментальный факт  теории фирмы: в точке локального рыночного равновесия (x01, x02) предельная норма замены R12(x01,x02) первого ресурса вторым равна отношению p1/p2 рыночных цен на эти ресурсы.

Поскольку х01,и x02 получаются в виде решения системы  уравнений (1), постольку x01 и х02 есть функции цен (p0, р1, р2), т.е.

x01= d1(p0, р1, р2), x02= d2(p0, р1, р2). (5)

ЧТО ТАКОЕ ФУНКЦИИ СПРОСА НА РЕСУРСЫ?

 

Выражения (5) называются функциями спроса на ресурсы  (затраты). Их значения х01 и х02 выражают оптимальные выборы затрат (использования) ресурсов как функции цены p0 выпускаемой  продукции и цен p1, p2 на ресурсы x1, x2, соответственно.

ЧТО ТАКОЕ ФУНКЦИЯ ПРЕДЛОЖЕНИЯ ВЫПУСКА?

 

Подставив функции (5) в производственную функцию у= f(x1,x2), получим выражение

y0 = f(d1(p0, р1, р2), d2(p0, р1, р2))=s(p0, p1, p2),

которое называется функцией предложения выпуска.

Функции спроса на ресурсы и функция предложения выпуска являются однородными нулевой степени по всем своим аргументам p0, p1 и p2. То есть

 

d1(t∙p0, t∙р1, t∙р2) = d1(p0, р1, р2), d2(t∙p0, t∙р1, t∙р2)=d2(p0, р1, р2), s(t∙p0,t∙p1,t∙p2)=s(p0,p1, p2)

 

для любого числа t>0.

 

Свойство однородности означает, что одновременное изменение всех цен p0, p1 и p2 в одно и то же число раз t (т. е. при изменении масштаба, но не структуры цен) не меняются x01, x02, и y0, что важно с  содержательной точки зрения. С математической точки зрения однородность нулевой степени функции спроса и функции предложения является простым фактом, ибо максимизация функции прибыли PR(x1,x2) = р0∙f(x1,x2)  - (p1∙x1+ р2∙x2) сводится к системе уравнений (2), поскольку на  множитель t>0 можно сократить.

 

ФУНКЦИИ СПРОСА НА ФАКТОРЫ (РЕСУРСЫ) В СЛУЧАЕ КРАТКОСРОЧНОГО ПРОМЕЖУТКА.

В случае краткосрочного промежутка рассмотрим конкретный пример, когда второй ресурс фирма может использовать только в объеме, равном x#2>0. Тогда задача максимизации прибыли  превращается в задачу максимизации функции одной переменной:

PR(x1,x#2) = р0∙f(x1,x#2)  - (p1∙x1+ р2∙x#2).

И вместо системы уравнений (1) появляется только одно уравнение:

р0∙∂f(x1,x#2)/∂x1=p1 .  (6)

Как и в предыдущем случае, считаем (исходя из содержательных  экономических соображений), что уравнение (6) имеет единственное  решение x1=x#1, (х#1 зависит от х#2, т.е. х#1= x#1(х#2), следовательно, в случае краткосрочного промежутка локальное рыночное равновесие есть вектор (x#1, х#2). С помощью рисунка 5 дадим ему наглядную геометрическую интерпретацию. Если бы объем х#2 второго ресурса не был лимитирован, то, как видно из рисунка 5, локальным  рыночным равновесием была бы точка касания (х01,x02), в которой тот же объем выпускаемой продукции (для точек (x#1, х#2) и (х01,x02) изокванта одна и та же)  получился бы при  меньших издержках  производства (изокоста,  содержащая точку (x#1, х#2), расположена «северо- восточнее» изокосты,  содержащей точку (х01,x02)). В точке (x#1, х#2)  локального рыночного  равновесия содержащие ее изокванта и изокоста пересекаются, но не  касаются. В  рассматриваемом случае на самом деле х#1=x#1(х#2,p0, p1, p2), это и есть функция спроса на первый ресурс при фиксированном объёме х#2 второго ресурса.

 

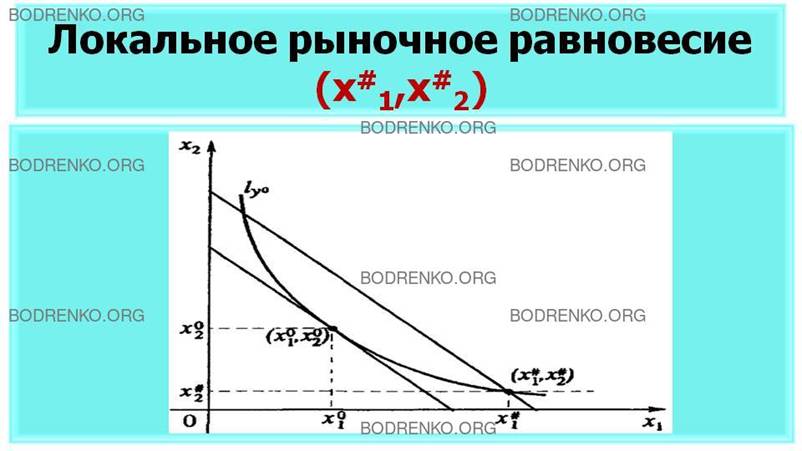
Рисунок 5. Локальное рыночное равновесие (x#1, х#2).

 

Функция предложения выпуска имеет вид:

 

Y=f(x#1(х#2,p0, p1, p2), х#2).

Может случиться так, что точки (x#1, х#2) и (х01,x02) сольются в одну, и тогда получится та ситуация, которая уже была проанализирована в предыдущем случае.

РАЗДЕЛ 2. КОМБИНАЦИЯ РЕСУРСОВ (ФАКТОРОВ ПРОИЗВОДСТВА), МАКСИМИЗИРУЮЩАЯ ОБЪЁМ ВЫПУСКА ПРИ ОГРАНИЧЕНИИ НА ЗАТРАТЫ.

Для случая долговременного промежутка рассмотрим задачу  максимизации объема выпускаемой продукции при ограничении затрат на приобретение ресурсов (факторов), т.е. рассмотрим задачу 1:

 

f(x1,x2) => max , (7)

при условии, что

p1∙x1+ р2∙x2≤V, (8)

х1≥0,  x2≥0. (9)

Величина V не обязательно равна величине С0=p1∙x01+ р2∙x02  (см. соотношение (*)).

Решение этой задачи математического программирования допускает наглядную геометрическую интерпретацию (см. рисунок 6).

 

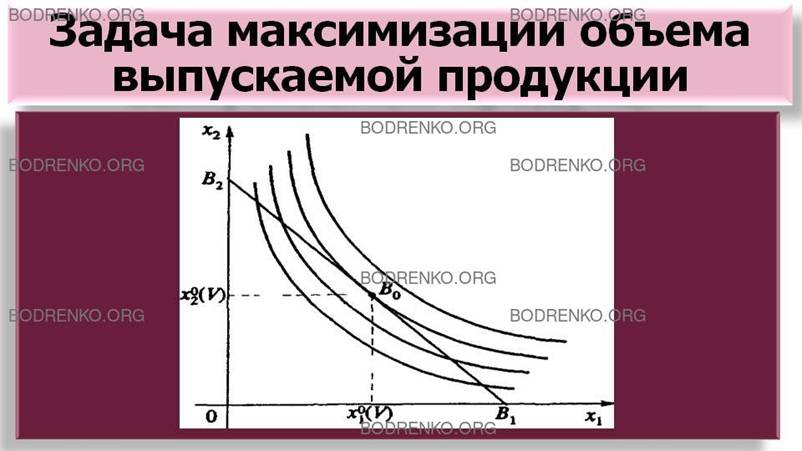
Рисунок 6. Задача максимизации объема выпускаемой продукции.

 

Ограничениям (8) и (9) соответствует треугольник ОВ1В2 плоскости Ox1x2.

Максимизация функции (7) геометрически соответствует тому, что мы переходим на все более «северо-восточные» изокванты, пока они имеют еще общие точки с треугольником OB1B2 (прямая (B1B2) имеет уравнение p1∙x1+ р2∙x2=V). Изокванты - гладкие линии,  выпуклые к точке О(0,0) (а это так, потому что f(x1,x2) не произвольная функция двух переменных, а производственная функция, т.е. функция,  удовлетворяющая определенным требованиям гладкости и выпуклости), поэтому решению задачи (7), (8), (9) соответствует изокванта,  которая касается гипотенузы (изокосты) (В1В2) в точке В0. Любая  изокванта, расположенная «северо-восточнее» этой изокванты,  содержащей точку В0, не подходит, ибо не имеет общих точек с  треугольником ОВ1В2. Координаты точки B0 (x01(V), x02(V))  и дают решение задачи(8), (9), (10).

В связи с тем, что это решение (x01(V), x02(V))  обращает ограничение (8) в равенство p1∙x1+ р2∙x2=V , вместо задачи (7), (8), (9) можно рассмотреть более простую задачу на условный экстремум

f(x1,x2) => max , (7)

при наличии ограничения

p1∙x1+ р2∙x2=V, (10)

(х1≥0,  x2≥0), заданного в виде равенства.

Задачи (7), (8), (9) и (7), (10) разные, но решение (x01(V), x02(V))  у них одно и то же (в случае отсутствия так называемых угловых решений, которые здесь не рассматриваются).

 

Поскольку сумма  p1∙x1+ р2∙x2 равна издержкам производства, постольку целесообразно заменить V на  С,  и формально перейти к задаче максимизации  объема выпускаемой продукции для случая долговременного  промежутка при фиксированных издержках производства С (величина С играет роль параметра и не обязательно равна величине С0 (см. соотношение (*)):

f(x1,x2) => max , (7)

при наличии ограничения

p1∙x1+ р2∙x2=С, (11)

(х1≥0,  x2≥0).

Геометрическое решение задачи (7), (11) также наглядно  очевидно (см. рисунок 7): следует переходить на все более «северо-восточные» изокванты до тех пор, пока они продолжают иметь общие точки с изокостой, соответствующей фиксированным издержкам производства С.

 

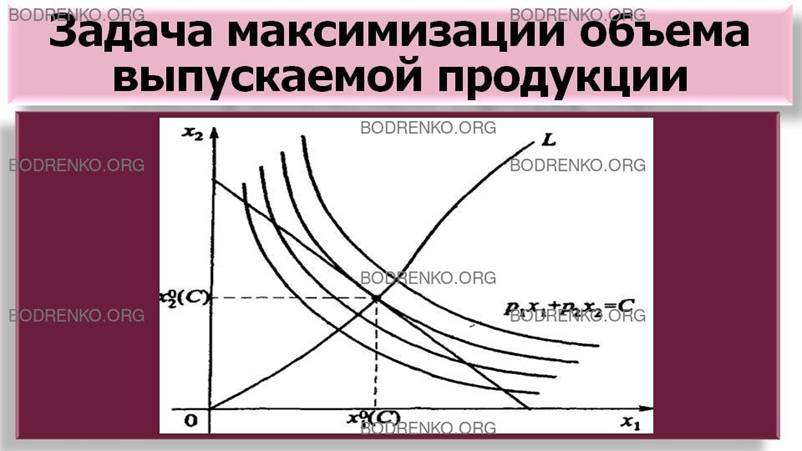
Рисунок 7. Решение задачи максимизации выпуска – точка (x01(С), x02(С)).

 

Ясно, что решением задачи максимизации выпуска будет точка (x01(С), x02(С)) касания последней из допустимых изоквант и фиксированной изокосты  p1∙x1+ р2∙x2=С.  Эта точка касания зависит от величины издержек производства С (поэтому и  написано (x01(С), x02(С))). Если издержки производства С изменятся, то изменится, вообще говоря, и точка (x01(С), x02(С)) .

 

ЧТО ТАКОЕ ДОЛГОВРЕМЕННАЯ ЛИНИЯ РАЗВИТИЯ ФИРМЫ?

 

Множество точек {(x01(С), x02(С))}, соответствующих различным значениям С, образуют линию Г (см. рисунок 7), которая называется долговременной линией развития фирмы. Точка (x01, x02) локального рыночного равновесия фирмы обязательно принадлежит линии L.

Решим задачу (7), (11) формально с помощью функции Лагранжа

L(x1,x2, λ) = f(x1,x2) + λ(C –  p1∙x1 – р2∙x2).

Для функции Лагранжа выписываем систему уравнений:

 

∂(L(x1,x2, λ))/∂x1 =0,

∂(L(x1,x2, λ))/∂x2 =0,

∂(L(x1,x2, λ))/∂λ =0.

 

или в развернутом виде

∂(f(x1,x2))/∂x1=λ∙p1,

 

∂(f(x1,x2))/∂x2=λ∙p2,

 

C – p1∙x1 – р2∙x2 =0. (12)

 

Критическая точка ((x01(С), x02(С), λ0(C)) функции Лагранжа, удовлетворяющая системе (12) и взятая без последней координаты  (множителя Лагранжа λ0(C))  т.е. точка (x01(С), x02(С)), и есть решение задачи (7), (11) максимизации выпуска при данных фиксированных издержках производства С. Подставив критическую точку ((x01(С), x02(С), λ0(C))  в первые два уравнения системы (12), получим два тождества.  Поделив почленно первое тождество на второе, получим, очевидно,  выражение (3) (множитель Лагранжа λ0(C)) сократится).   

 

Получили  аналитическое обоснование того, что в точке ((x01(С), x02(С)) изокванта и изокоста касаются (см. рисунок 7). Вообще говоря, критическая точка функции Лагранжа,  взятая без последней координаты, не обязана быть решением задачи (7), (11) на условный максимум. В случае же производственной функции f(x1,x2), удовлетворяющей определенным требованиям гладкости и выпуклости, критическая точка функции Лагранжа (без последней координаты) есть решение задачи (7), (11) на условный экстремум. Отметим также, что в случае  производственной функции f(x1,x2) имеем строгие неравенства: x01(С)>0, x02(С)>0, λ0(C)>0.

 

В разделе 1 этой лекции  в точке локального рыночного равновесия (х01,х02) были определены издержки производства, равные величине С0=p1∙x01+ р2∙x02  (равенство (*)). Если в ограничении (12) положить С=С0, то несложно показать, что   x01(С0)=x01,  x02(С0)=x02, а также, что 1/λ0(C0)=p0, т.е. величина, обратная множителю Лагранжа  λ0(C0), равна рыночной цене p0 единицы  выпускаемой фирмой продукции. Таким образом, предложена  естественная экономическая интерпретация множителя Лагранжа  λ0(C0).

Подставив x1=x01(С), x2=x02(С) в выражение y=f(x1,x2), получим, что

y=f(x01(С), x02(С))=F(C). (13)

То есть получим у= F(C) как функцию издержек производства С, а не как функцию y=f(x1,x2) объемов х1 и х2 затрачиваемых  (используемых) ресурсов. Выражение (13) называется значением задачи (7), (11).

Так построенная функция у= F(С) соответствует случаю  долговременного промежутка.

Имея функцию у= F(С), можно выписать выражение для  прибыли в терминах издержек производства:

 

PR(С) = p0∙F(C) – С  

 

(сравните с выражением для прибыли фирмы в терминах затрачиваемых (используемых) ресурсов - см. раздел 1).

Задача максимизации объема выпускаемой продукции при  фиксированных издержках производства С для случая краткосрочного промежутка, когда лимитирован объем х#2 второго ресурса, имеет вид

f(x1,x#2) => max , (14)

при наличии ограничения

p1∙x1+ р2∙x#2=С, (15)

(х1≥0).

Ограничимся наглядным геометрическим решением задачи (14), (15) (см. рисунок 8).

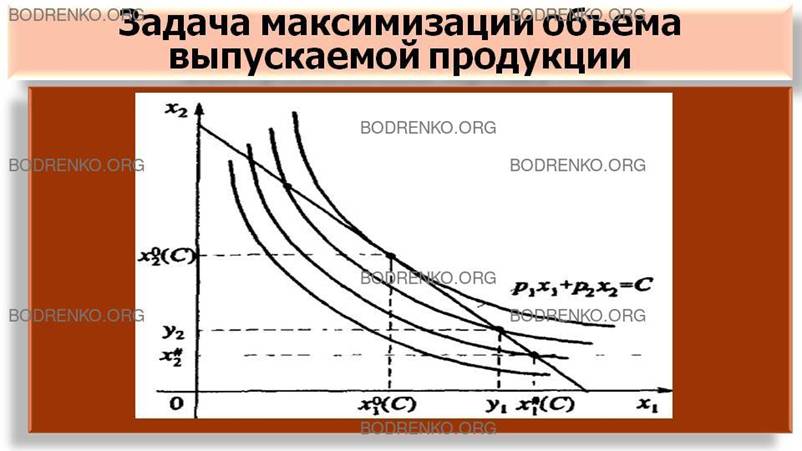
Рисунок 8. Задача максимизации объема выпускаемой продукции при  фиксированных издержках производства.

 

Перемещаемся по изоквантам на «северо-восток» до того момента, пока изокванта не пройдет через точку (х#1(С), х#2(С)), которая есть решение задачи (14), (15). От этой изокванты далее на «северо-восток» идти нельзя, так как в точках у=(y1,y2) - пересечения новых изоквант и фиксированной изокосты p1∙x1+ р2∙x2=С имеет место неравенство y2 ≠x#2 (см. рисунок 8).

Если бы условиях равенства x2=х#2 не было, то решением задачи  максимизации объема выпускаемой продукции была бы точка (x01(С), x02(С)) (см. рисунок 8), которая соответствует случаю долговременного  промежутка. Очевидно,

 

f(x01(С), x02(С))>f(x#1(C), х#2).

 

Так как изокванта,  проходящая через точку(x01(С), x02(С)), расположена «северо-восточнее» изокванты, проходящей через точку (x#1(C), х#2).

 

ВЫВОД. Получен важный результат теории фирмы: при одних и тех же издержках производства С объем выпускаемой продукции для долговременного промежутка больше (точнее не меньше) объема выпускаемой продукции для краткосрочного  промежутка. Эти объемы сравняются, если издержки производства С будут такими, что x02(C)=х#2, (см. рисунок 9). Горизонтальная прямая х2=х#2 называется краткосрочной линией развития производства фирмы.

 

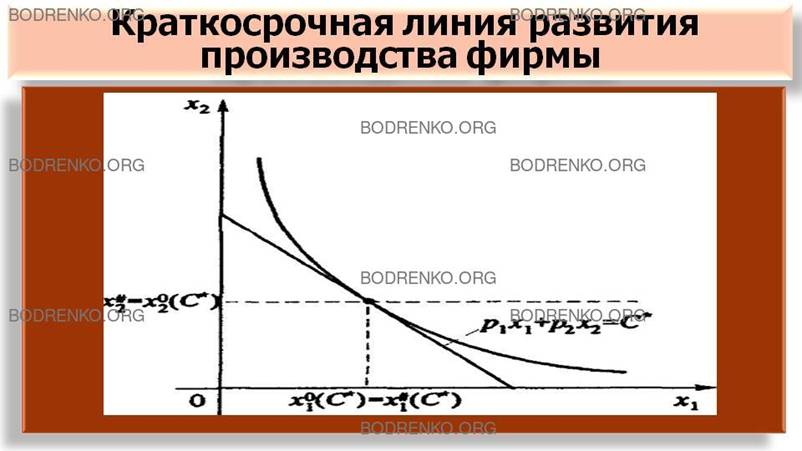
Рисунок 9. Краткосрочная линия развития производства фирмы.

 

РАЗДЕЛ 3. КОМБИНАЦИЯ РЕСУРСОВ (ФАКТОРОВ ПРОИЗВОДСТВА), МИНИМИЗИРУЮЩАЯ ИЗДЕРЖКИ ПРИ ФИКСИРОВАННОМ (ОБЩЕМ) ОБЪЁМЕ ВЫПУСКА.

Для случая долговременного промежутка рассмотрим задачу  минимизации издержек производства при фиксированном объеме у  выпускаемой продукции (т.е. рассмотрим задачу 2):

 p1∙x1+ р2∙x2=С(x1, x2) →min (16)

 

при условии, что

y=f(x1,x2), (х1≥0,  x2≥0). (17)

Геометрически решение задачи (16), (17) аналогично решению задачи (7), (10) (см. рисунок 9): в случае задачи (16), (17) следует перемещаться по изокостам на «юго-запад» (так как имеем задачу  минимизации) до тех пор, пока они продолжают иметь общие точки с изоквантой, соответствующей фиксированному объему y.

 

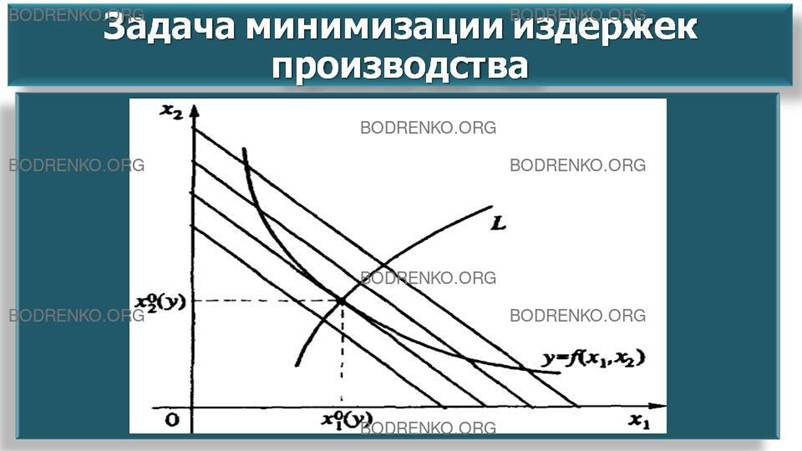
Рисунок 9. Графическое решение задачи минимизации издержек (16), (17).

 

Ясно, что решением задачи минимизации издержек будет общая точка (х01(y), x02(y)) изокосты и фиксированной изокванты. Эта точка  касания зависит от объема у,  поэтому и написано (х01(y), x02(y)). Если объем у изменится, то изменится и точка (х01(y), x02(y)).  

 

Множество точек {(х01(y), x02(y))}, соответствующих различным объемам у  выпускаемой продукции, образуют линию L (см. рисунок 9), которая,  очевидно, совпадает с линией L на рисунке 6.

Решим задачу (16), (17) формально с помощью функции Лагранжа

L(x1,x2,λ) = p1∙x1+ р2∙x2 + λ(y – f(x1,x2)) .

Для функции Лагранжа выписываем систему уравнений:

∂(L(x1,x2, λ))/∂x1 =0,

∂(L(x1,x2, λ))/∂x2 =0,

∂(L(x1,x2, λ))/∂λ =0.

 

Запишем эту систему в развернутом виде:

p1=λ∙∂(f(x1,x2))/∂x1,  p2=λ∙∂(f(x1,x2))/∂x2,  y – f(x1,x2)=0. (18)

 

Критическая точка (x01(y), x02(y), λ0(y)) функции Лагранжа,  удовлетворяющая системе (18) и взятая без последней координаты λ0(y)), т.е. точка (x01(y), x02(y)), и есть решение задачи (16), (17)  минимизации издержек при данном фиксированном объеме производства y.

Подставив точку (x01(y), x02(y), λ0(y)) в первые два уравнения системы (18), получим два тождества. Поделив почленно первое тождество на второе, получим, очевидно, выражение (3) (множитель λ0(y)  сократится, как и в случае раздела 2 множитель λ0(y)>0). Получили аналитическое обоснование того, что изокоста и изокванта  касаются в точке (x01(y), x02(y)) (см. рисунок 9). Характер взаимосвязи между критической точкой функции Лагранжа  без последней координаты λ0(y) и решением задачи (16), (17) минимизации может быть  прокомментирован здесь подобно тому, как это было сделано в разделе 2 для задачи максимизации.

В разделе 2 в точке локального рыночного равновесия (x01, x02) был определён объём производства у0=f(x01, x02). Если в ограничении (17) положить y=y0, то несложно показать,

что

 

x01(y0)=x01, x02(y0)=x02,

а также p0.

 

То есть множитель Лагранжа λ0(y0) равен рыночной цене p0 единицы выпускаемой продукции. Таким образом,  предложена естественная экономическая интерпретация множителя Лагранжа λ0(y0).

Подставив х1=x01(y), x2=x02(y) в выражение С(x1, x2)= p1∙x1+ р2∙x2, получим выражение для издержек

p1∙x01(y)+ р2∙x02(y) =C(y),

как функцию объема выпускаемой продукции, а не как  функцию С(x1,x2)= p1∙x1+ р2∙x2 объемов затрачиваемых (используемых) ресурсов.

 

Выражение С(у)=p1∙x01(y)+ р2∙x02(y)  называется значением задачи (16), (17).

 

Так построенная функция издержек С(у)  соответствует случаю долговременного промежутка. Имея выражение С(у), выпишем в явном виде представление прибыли в виде функции объемов у выпускаемой продукции:

PR(y) = p0∙y – С(у)

(сравните с выражением для прибыли фирмы в терминах  затрачиваемых (используемых) ресурсов - см. раздел 1). Выражение (PR(y)=p0∙y – С(у)) играет важную роль в микроэкономике.

Пусть (x01(С), x02(С)) и у=h(С) есть решение и значение задачи максимизации (7), (11) (см. раздел 1).

Пусть (x01(y), x02(y)) и C=C(y) есть решение и значение задачи минимизации (16), (17).

Пусть значение С в (12) равно значению С(y) задачи  минимизации (16), (17). Тогда значение задачи максимизации (7), (11) (см. раздел 2) будет равно у.

Наоборот, пусть значение у в (17) равно значению у=h(C) задачи максимизации (7), (11). Тогда значение задачи минимизации (16), (17) равно С. Таким образом, наблюдается взаимная зависимость задач (7), (11) и (16), (17) (см. рисунок 10).

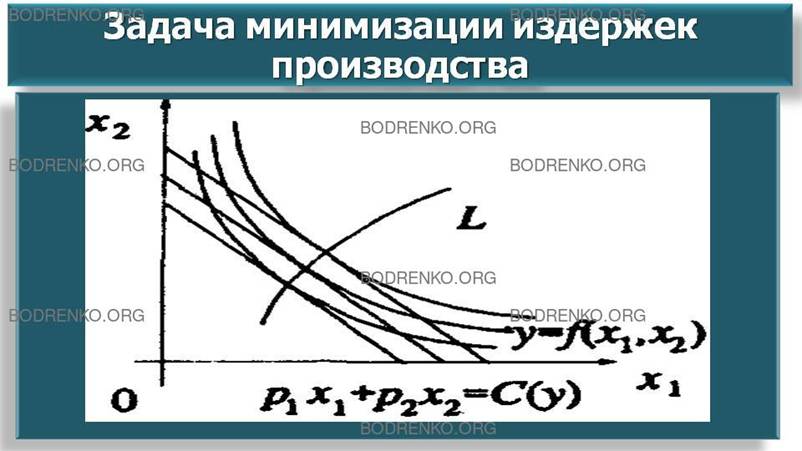
Рисунок 10. Решение и значение задачи минимизации (16), (17).

Задача минимизации издержек производства при фиксированном объеме y выпускаемой продукции для случая краткосрочного  промежутка, когда фиксирован объем х#2 второго ресурса, имеет вид (у играет роль параметра):

p1∙x1+ р2∙x#2=С(x1, x#2) →min , (19)

 

при условии, что

y=f(x1,x2), (х1≥0). (20)

Ограничимся наглядным геометрическим решением задачи (19), (20) (см. рисунок 11).

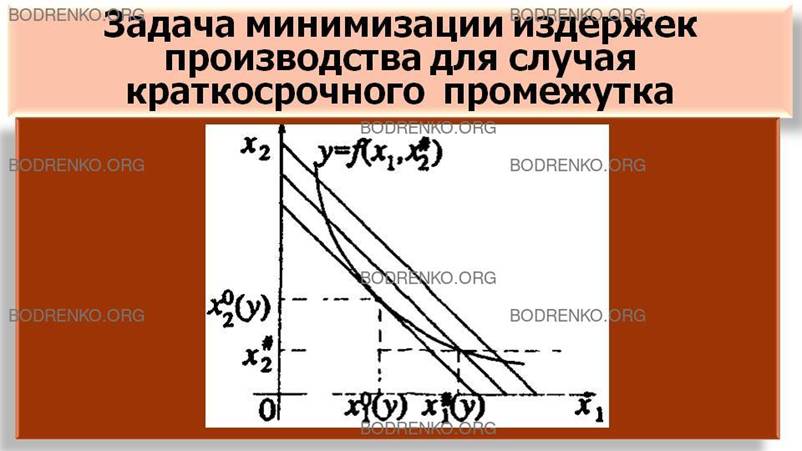
Рисунок 11. Задача минимизации издержек производства при фиксированном объеме y выпускаемой продукции.

 

ВЫВОД. Имеет место важный результат теории фирмы: при одном том же объеме у выпускаемой продукции издержки производства для случая долговременного промежутка меньше  (точнее не больше) издержек производства для случая краткосрочного промежутка. Эти издержки производства равны друг другу, если объем y* производства будет таким, что х01(y*) =х#2 (см. рисунок 12).

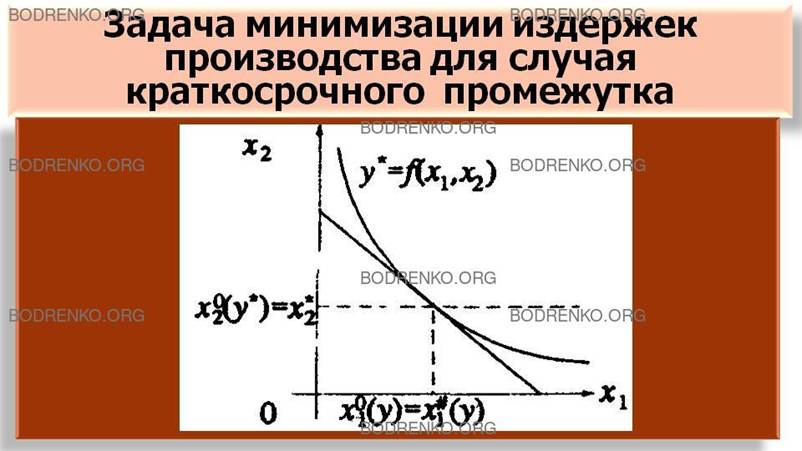
Рисунок 12. Издержки производства при фиксированном объеме y выпускаемой продукции.

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Замков О.О., Толстопятенко А.В., Черемных Ю.М. Математические методы в экономике: Учебник. 2-е изд. - М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. — 368 с.

 

[2] Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

[3] Шелобаев С. И. Математические методы и модели в экономике,  финансах, бизнесе: Учеб. пособие для вузов. — М.: ЮНИТИ - ДАНА, 2001. - 367 с.

[4] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).

 

[5] Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш,  Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.:  ЮНИТИ, 1999. - 391 с.