Математические методы исследования экономики.

 

Лекция 8

 

Тема лекции 8: «Методы построения и использования производственных функций»

Разделы лекции:

 

1. Производственные функции как основа описания закономерностей производства.

2. Формальные свойства производственных функций.

3. Производственные функции с двумя ресурсами.

РАЗДЕЛ 1. ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ КАК ОСНОВА ОПИСАНИЯ ЗАКОНОМЕРНОСТЕЙ ПРОИЗВОДСТВА.

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ.

 

Производственными функциями (в широком смысле) называют соотношения между используемыми в производстве материальными благами и трудовыми ресурсами (называемыми в совокупности производственными ресурсами) и выпускаемой продукцией.

Пусть в модели рассматривается n производственных  ресурсов. Количество i-го ресурса, используемого (или потребляемого) в течение некоторой единицы времени, обозначим через хi. Пусть выпускается m продуктов, причем объем выпуска j-го продукта обозначен через уj. Производственная функция связывает  значения вектора продукции у=(y1, …, ym) со значениями вектора ресурсов х=(x1, …, xn):

F (x, у, а) = 0, (1)

где а = (a1, ..., ар) — вектор параметров производственной  функции.

Соотношение (1) может быть векторным, т. е. оно может состоять из нескольких равенств. Производственная функция (1) может быть задана не только в аналитическом виде (т. е. в виде системы функций), но и в виде таблицы. Описание связи между использованием ресурсов и выпуском продукции в виде (1)  подразумевает, что не учитываются эффекты, связанные с  продолжительностью производственного цикла, т. е. с периодом между затратами ресурсов и выпуском продукции. Далее в этом  разделе будем предполагать, что это возможно в силу того, что единица времени, для которой строится производственная  функция, значительно превосходит продолжительность  производственного цикла.

Описание элементарной производственной единицы начинается с формулировки списка ресурсов и номенклатуры продукции с указанием характерных значений и пределов изменения этих  величин. Характерные значения объемов используемых ресурсов определяют единицы измерения, используемые в  производственных функциях. Если производится всего несколько тонн  продукции, то выпуск измеряют в тоннах; если тысячи тонн — то  соответственно в тысячах тонн. Часто используются безразмерные единицы, т. е. выпуск продукции и использование ресурсов  измеряются, например, в отношении к выпуску продукции и  использованию ресурсов некоторого базового года.

Следует отметить, что не все величины, воздействующие на производство, могут быть описаны количественно. Так,  например, не всегда удается описать количественно такие важные факторы, как концентрация и рационализация производства,  организация труда, структура управления и т.д. В этом случае их  влияние пытаются учитывать через воздействие этих факторов на  ресурсы, на структуру производственной функции и ее параметры. Материальные производственные ресурсы необходимо  различать по способам их расходования в производственных процессах. Обычно выделяют материальные ресурсы двух типов: предмет труда (сырье) и основные фонды (здания, оборудование и т. д.).

Ресурсы первого типа в процессе производства в течение одного производственного цикла (т. е. периода выпуска продукции)  расходуются полностью, ресурсы второго типа используются в  течение значительного числа производственных циклов.

Вместо общего представления производственной функции в виде (1) часто используют два частных случая:

1) функции выпуска, в которых в качестве независимых  переменных берутся затраты ресурсов, а функцией является выпуск

y=f(x,a),  (2)

2) функции производственных затрат, в которых независимой переменной является выпуск, а функцией — затраты

x = h(y, a). (3)

Подчеркнем еще раз, что в соотношениях (2) и (3)  величины y, х и а могут быть многокомпонентными или векторными.

В том случае, когда вектор ресурсов х является  многокомпонентным, между функциями выпуска и функциями затрат возникает принципиальное различие. В функции выпуска (2) возможны различные сочетания количеств производственных ресурсов, что приводит к тому, что один и тот же объем продукции может быть произведен, вообще говоря, при разных сочетаниях  количеств ресурсов. В функции затрат (3) задание выпуска  продукции полностью определяет затраты ресурсов. Поэтому функции затрат используются в том случае, когда в описываемой  элементарной экономической единице отсутствует возможность  замещения одного ресурса другим. Функции выпуска используются  тогда, когда такая замена допустима. Отметим, что в экономической литературе часто под термином «производственная функция» (в узком смысле) подразумевают функцию выпуска (2).

ЧТО ТАКОЕ МНОЖЕСТВО ПРОИЗВОДСТВЕННЫХ ВОЗМОЖНОСТЕЙ?

 

С понятием производственной функции (в широком смысле) тесно связано понятие МНОЖЕСТВА ПРОИЗВОДСТВЕННЫХ  ВОЗМОЖНОСТЕЙ, которое определяется как множество всех возможных  сочетаний затрат трудовых и материальных ресурсов и выпусков  продукции, то есть имеет вид:

{(х, y)}ÎG(a), (4)

где G(a) — некоторое множество в пространстве ресурсов и  продукции, зависящее от вектора параметров а.

ПРИМЕР 1.

 

Приведем простой пример множества технологических  возможностей: Пусть имеются единственный ресурс х и единственный продукт у. Проинтерпретировать эти величины можно, например, как  количество техники, приходящейся на единицу площади  сельскохозяйственных угодий в некотором районе, и урожайность полевых культур. При этом предполагается, что количество остальных  ресурсов (трудовых ресурсов, минеральных удобрений и т. д.)  остается без изменений, поэтому они не включены в производственную функцию в явном виде. Множество производственных  возможностей зададим соотношением

0≤у≤х^α,  х≥0, (5)

где α— параметр, удовлетворяющий соотношению 0<α<1.

Множество производственных возможностей изображено на рисунке 1.

 

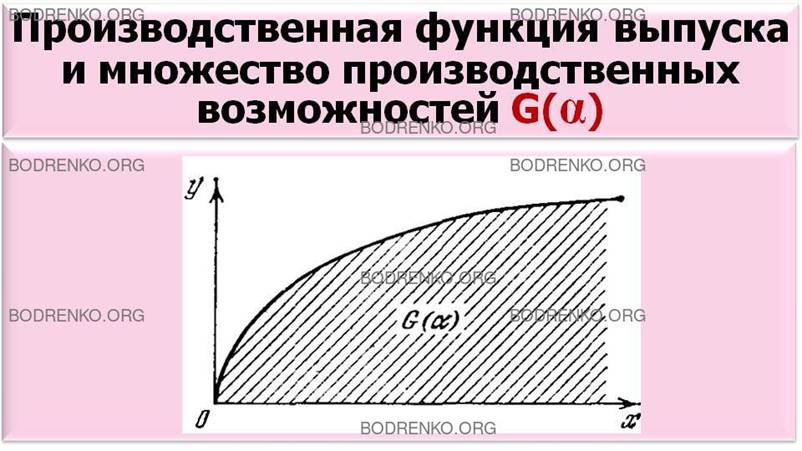
Рисунок 1. Производственная функция выпуска и множество производственных возможностей G(α).

 

Связь между производственной функцией и множеством  производственных возможностей  устанавливается следующим образом. Предположим, что производство ведется эффективно, т. е. при данном  количестве ресурсов выпускается  максимально возможное количество  продукции. Тогда имеет смысл  рассматривать не все множество  производственных возможностей (5), а  только его границу

у = х^α,  х≥0 (0<α<1). (6)

Таким образом, мы получили производственную функцию в виде функции выпуска. Если же с самого начала задана  производственная функция в виде (6), то множество производственных возможностей можно получить, предполагая, что вместе с производством некоторого количества продукции с помощью тех же ресурсов можно выпустить и меньшее количество продукции. Тогда из (6) с учетом того, что выпуск неотрицателен, сразу же получаем (5). Аналогичным образом от описания в виде множества  производственных возможностей (5) можно перейти к функции  затрат. Для этого надо предположить, что производство данного неотрицательного объема продукции у  достигается при минимальных затратах ресурса х. Из (5) получаем функцию

x = y^1/α,  y≥0, (7)

которая имеет вид функции затрат (3).

Заметим, что соотношения (6) и (7)  описывают одну и ту же зависимость. На рисунке 2 изображены функция затрат (7) и множество производственных возможностей (5).

 

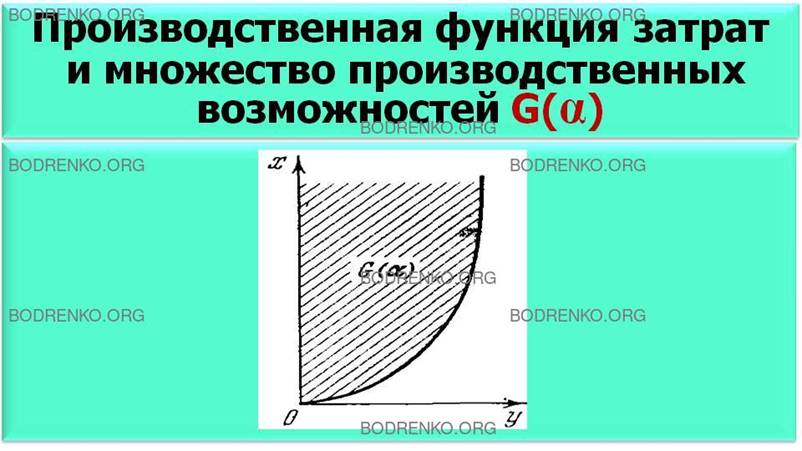
Рисунок 2. Производственная функция затрат и множество производственных возможностей.

 

ЗАМЕЧАНИЕ.

 

Конечно, такая простая связь между множеством производственных возможностей и производственными функциями  устанавливается лишь в случае одного продукта и одного ресурса. В общем случае переход от множества производственных  возможностей (4) к производственной функции (1) требует построения множества всех эффективных точек множества (4), т. е. всех таких объемов затрачиваемых ресурсов и выпускаемой  продукции, что при данных затратах нельзя выпустить большее количество хотя бы одного вида продукции, не уменьшив  производства других видов продукции; кроме того, данного выпуска  нельзя добиться при меньших затратах хотя бы одного ресурса, не увеличив при этом затраты других ресурсов. Помимо чисто  математических проблем переход от описания в виде множества производственных возможностей (4) к производственной  функции (1) ставит следующие принципиальные вопросы. На каком основании мы считаем, что будут реализовываться только  эффективные точки множества G(a)? Имеется ли экономический механизм, приводящий к реализации только эффективных точек? Таким образом, здесь от чисто производственно-технологических вопросов приходится переходить к социально-экономическим  проблемам. С этим фактом нам еще придется столкнуться при  обсуждении вопроса о построении производственных функций. Пока же заметим, что в некоторых случаях множество производственных возможностей удобнее рассматривать вместо производственной функции из чисто математических соображений.

ОДНОРЕСУРСНЫЕ ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ.

 

Как было отмечено выше, производственная функция выпуска -  это функция, независимая  переменная x которой принимает значения объемов затрачиваемого или используемого ресурса (фактора производства), а зависимая  переменная y принимает значения объемов выпускаемой продукции:

 

y=f(x). (8)

 

В формуле (8) x (где х ≥ 0) и у (где у ≥ 0) - числовые величины, т.е. у =f(x) есть числовая функция одной переменной х.

В связи с этим  производственная функция (ПФ) y=f(x) называется одноресурсной или однофакторной ПФ, ее область определения - множество неотрицательных действительных чисел (т.е. х≥0). Запись у =f(x) означает, что если ресурс затрачивается или используется в количестве х единиц, то продукция выпускается в количестве у=f(x) единиц. Символ f - знак функции - является характеристикой производственной  системы, преобразующей ресурс в выпуск. Символ f связывает между собой независимую переменную х с зависимой переменной у. В микроэкономической теории принято считать, что у - это  максимально возможный объем выпуска продукции, если ресурс  затрачивается или используется в количестве х единиц. В макроэкономике такое понимание не совсем корректно: возможно, при другом  распределении ресурсов между структурными единицами экономики выпуск мог бы быть и большим. В этом случае ПФ - это  статистически устойчивая связь между затратами ресурса и выпуском. Более правильной является символика у=f(x, a), где a - вектор  параметров ПФ.

 

ПРИМЕР 2. Возьмем ПФ f в виде: f(x)=а∙х^b, где х – величина затрачиваемого ресурса (например, рабочего времени), f(x) – объем выпускаемой продукции (например, число готовых к отправке  холодильников). Величины а и b - параметры ПФ f. Здесь а и b -

положительные числа, и число b<1, вектор параметров есть  двумерный вектор (а,b).

 

График Γ производственной функции у= а∙х^b, изображен на рисунке 3.

 

 

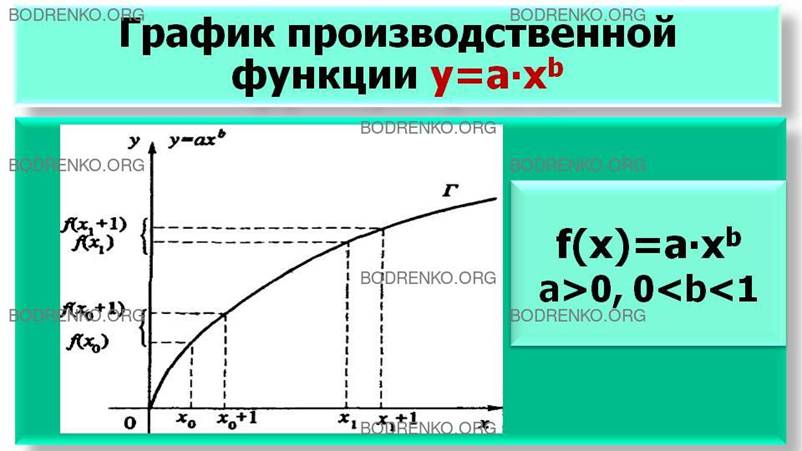
Рисунок 3. График производственной функции у= а∙х^b.

 

На этом графике (рисунок 3) видно, что с ростом величины затрачиваемого ресурса x объем выпуска у растет, однако при этом каждая дополнительная единица ресурса дает все меньший прирост объема у  выпускаемой продукции. Отмеченное обстоятельство (рост объема у и уменьшение прироста объема у с ростом величины х) отражает фундаментальное положение экономической теории (хорошо  подтверждаемое практикой), называемое законом убывающей  эффективности. ПФ у= а∙х^b является типичным представителем широкого класса однофакторных ПФ.

 

ПФ могут иметь разные области использования. Принцип  «затраты – выпуск» может быть реализован как на микро-, так и на макроэкономическом уровне. Сначала остановимся на  микроэкономическом уровне. ПФ у =а∙х^b, рассмотренная выше, может быть использована для описания взаимосвязи между величиной  затрачиваемого или используемого ресурса х в течение года на отдельном предприятии (фирме) и годовым выпуском продукции у этого  предприятия (фирмы). В роли производственной системы здесь  выступает отдельное предприятие (фирма) - имеем микроэкономическую ПФ (МИПФ). На микроэкономическом уровне в роли  производственной системы может выступать также отрасль, межотраслевой производственный комплекс. МИПФ строятся и используются в  основном для решения задач анализа и планирования, а также задач прогнозирования.

 

ПФ может быть использована для описания взаимосвязи между годовыми затратами труда в масштабе региона или страны в целом и годовым конечным выпуском продукции (или доходом) этого региона или страны в целом. Здесь в роли производственной  системы выступает регион или страна в целом (точнее хозяйственная система региона или страны) - имеем макроэкономический уровень и макроэкономическую ПФ (МАПФ). МАПФ строятся и активно используются для решения всех трех типов задач (анализа,  планирования и прогнозирования).  Точное толкование понятий затрачиваемого (или используемого) ресурса и выпускаемой продукции, а также выбор единиц их  измерения зависят от характера и масштаба производственной системы, особенностей решаемых (с помощью ПФ) задач (аналитических, плановых, прогнозных), наличия исходных данных.

 

В КАКИХ ПОКАЗАТЕЛЯХ ИЗМЕРЯЮТСЯ ЗАТРАТЫ И ВЫПУСК НА МИКРОЭКОНОМИЧЕСКОМ УРОВНЕ?

 

На  микроэкономическом уровне затраты и выпуск могут измеряться как в натуральных, так и в стоимостных единицах (показателях). Годовые затраты труда могут быть измерены в человеко-часах (объем  человеко-часов - натуральный показатель) или в рублях выплаченной заработной платы (ее величина - стоимостный показатель); выпуск  продукции может быть представлен в штуках или в других  натуральных единицах (тоннах, метрах и т.п.) или в виде своей  стоимости.

 

В КАКИХ ПОКАЗАТЕЛЯХ ИЗМЕРЯЮТСЯ ЗАТРАТЫ И ВЫПУСК НА МАКРОЭКОНОМИЧЕСКОМ УРОВНЕ?

 

На макроэкономическом уровне затраты и выпуск измеряются, как правило, в стоимостных показателях и представляют собой  стоимостные (ценностные) агрегаты, т.е. суммарные величины  произведений объемов затрачиваемых (или используемых) ресурсов и выпускаемых продуктов на их цены.

 

РАЗДЕЛ 2. ФОРМАЛЬНЫЕ СВОЙСТВА ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ.

 

СВОЙСТВА ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ. Рассмотрим некоторые наиболее общие свойства производственных функций, имеющих форму (2), т. е. функций выпуска, допускающих, вообще говоря, замену одного ресурса другим. В этом разделе будут изучены функции с одним продуктом и несколькими ресурсами  (трудовыми и материальными). Вектор параметров а в соотношении (2) будем опускать, считая, что параметры уже определены и их влияние нас не интересует. Тогда функция выпуска приобретает вид

y=f(x) (9)

где у — скаляр, х=(х1,..., хn) — вектор. Соотношение (9)  задано при неотрицательных значениях компонент вектора  ресурсов х.

Обычно относительно производственной функции (9) делают предположение, очень удобное с математической точки зрения,— предположение о непрерывном изменении переменных х и  достаточно плавном изменении выпуска при изменении затрат ресурсов. В математической форме эти предположения имеют следующий вид: функция (9) задана при всех неотрицательных значениях составляющих вектора х (как принято говорить, НА  НЕОТРИЦАТЕЛЬНОМ ОРТАНТЕ) и является непрерывной (или нужное  число раз дифференцируемой) функцией своих аргументов. На  практике, ресурсы и продукция зачастую не могут меняться  непрерывно — их количество дискретно и измеряется, например, в штуках. Описание с помощью переменных, принимающих  любые вещественные значения, и непрерывных функций означает в таких случаях, что число выпускаемых и потребляемых единиц достаточно велико, чтобы дискретностью можно было пренебречь. Перейдем к формулировке предположений, имеющих под  собой экономическое обоснование. Подчеркнем, что хотя  формулируемые ниже предположения кажутся довольно естественными и часто используются при изучений свойств производственных функций, можно привести много примеров, где они не  выполняются. Поэтому всякий раз после формулировки предположения мы будем обсуждать его.

1) ПЕРВОЕ ПРЕДПОЛОЖЕНИЕ. Производство невозможно при отсутствии хотя бы одного ресурса, т. е.

f(0, х2, ..., xn) = 0,

f(x1, 0, …, xn)=0

…

f(x1, …, 0) = 0.

Это предположение означает, что каждый из ресурсов  необходим хотя бы в малых количествах. Полное его отсутствие не  может быть компенсировано другими ресурсами. Заметим, что это условие выполняется для функции (6).

Вообще говоря, предположение 1) обязательно только для трудовых и еще некоторых действительно незаменимых  ресурсов — как, например, семян при выращивании зерна. Другие те ресурсы (скажем, удобрения в полеводстве) не обязательны,  урожай может быть получен и в их отсутствие.

 

2) ВТОРОЕ ПРЕДПОЛОЖЕНИЕ. При увеличении затрат производственных ресурсов выпуск продукции не уменьшается.

В математической форме это выглядит так:

f(x*)≤ f(x**) при х*≤ х**. (10)

Если функция f(x) дифференцируема, то (10) можно переписать

в эквивалентной форме: при х>0

∂f(x)/∂xi ≥0, i=1, ..., n.  (11)

Величина ∂f(x)/∂xi называется предельной эффективностью (или производительностью) i-го ресурса.

Величина предельной  эффективности, вообще говоря, зависит от точки х, в которой берется производная. Предельная эффективность характеризует  отношение прироста выпуска продукции к малому приросту количества производственного ресурса.

Заметим, что предположение (10), являющееся на первый взгляд очевидным, также выполняется не всегда. Так, при  увеличении количества удобрений, приходящихся на единицу  площади, производство зерна сначала растет, а затем начинает  убывать. Этот факт должен находить отражение в производственных функциях, которые не будут удовлетворять предположению (10).

Для производственных функций, не удовлетворяющих  соотношениям (10) или (11), вводится понятие экономической области  в случае дифференцируемых функций это — множество таких сочетаний ресурсов х, для которых выполняется соотношение (11).

 

Использование ресурсов в сочетаниях, не попадающих в экономическую область, бессмысленно с экономической точки зрения. Для функций (8), имеющих непрерывные производные, границами экономической области являются поверхности ∂f(x)/∂xi=0, которые часто называют разделяющими поверхностями.

Эффективность использования ресурса можно  охарактеризовать не только предельной эффективностью, описывающей  свойство производственной функции в некоторой точке, но и  интегральным показателем — средней эффективностью ресурса,  определяемой как f(x)/xi.

 

ПРИМЕР 3.  Средняя эффективность обычно отличается от предельной эффективности. Так, для производственной  функции (6) при х>0 получаем

∂f/∂x = α∙x^α-1 > 0.

Отсюда следует, что для функции (6) экономическая область совпадает с областью определения функции, Далее, заметим, что f(x)/x= x^α-1. В силу того, что 0<α<1, для этой  производственной функции предельная эффективность меньше средней.

Помимо предельной и средней эффективностей в качестве  характеристики изменения выпуска продукции при увеличении  затрат ресурсов используют также отношение этих величин,  которое принято называть эластичностью выпуска по отношению к изменению затрат i-го ресурса и обозначать

Ei(x) = (xi/f(x))∙(∂f/∂xi). (12)

 

При анализе эффективности использования ресурсов  исследователи часто интересуются вопросом о том, на сколько  процентов возрастет объем продукции при увеличении затрат ресурса на 1%, Как легко заметить, эластичность выпуска по отношению к изменению затрат близка к этой величине, Величину Ei(x)   можно вычислять по более удобной формуле, эквивалентной (12).

Поскольку при xi>0 и f(x)>0 имеем dxi/xi = d(ln хi) и dx/f(x)=d(ln f(x)), то (12) эквивалентно соотношению

 

Ei(x) = (∂(ln f(x))/∂(ln xi). (12`)

 

ПРИМЕР 4. Для производственной функции (6) имеем

E(x) = d(ln f(x))/d(ln x) = d(α∙ln x)/d(ln x) = α.

 

Таким образом, эта производственная функция  характеризуется постоянной эластичностью выпуска по отношению к  изменению ресурса. На рисунке 4 изображен графики производственной функции (6), ее предельной и средней эффективностей, а также эластичности выпуска по ресурсу.

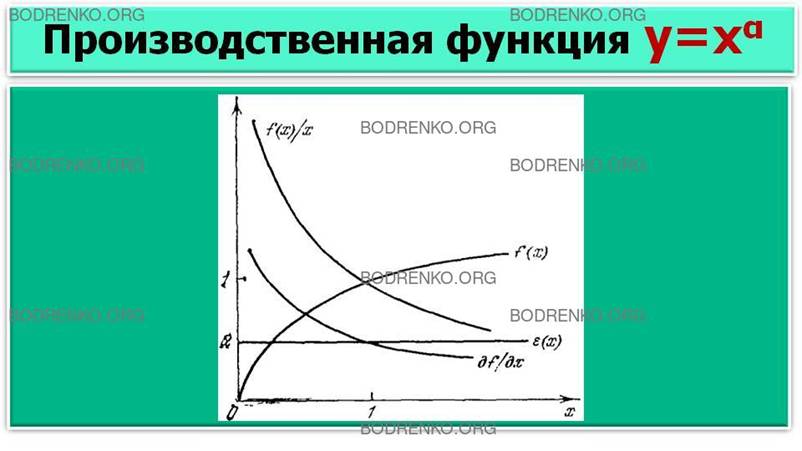
Рисунок 4. Графики ПФ, ее предельной и средней эффективностей.

 

 

3) ТРЕТЬЕ ПРЕДПОЛОЖЕНИЕ. По мере увеличения  количества одного ресурса при постоянных количествах других  предельная эффективность использования этого ресурса не  возрастает. Математически это требование для дважды  дифференцируемых производственных функций (8) выглядит так:

∂2f(x)/∂xi∂xi ≤0 , i=1, …, n. (13)

Легко проверить, что для производственной функции (6) это условие выполняется. Оно означает, что рост вооруженности средствами производства приводит к росту выпуска продукции, по темп роста выпуска продукции все время падает. В случае экстенсивного роста производства; т. е, роста только за счет  количества ресурсов, без  повышения эффективности их  использования на основе достижений научно-технического прогресса, соотношение (13) имеет  разумную интерпретацию:  поскольку каждая следующая  единица производственного  ресурса, количество которого  возрастает, должна соединяться со все меньшим приходящимся на нее количеством других  ресурсов, эффективность  использования этого ресурса уменьшается. Если количество тракторов в экономической системе,  описываемой функцией (6), будет увеличиваться, а численность трактористов оставаться прежней, то это приведет к росту числа тракторов в расчете на  одного тракториста. В условиях неизменных технологии проведения  полевых работ, квалификации трактористов и технических  характеристик тракторов это увеличение фондовооруженности хотя и  вызовет некоторый рост производства, однако тракторы будут  использоваться все менее эффективно. Часть времени они будут простаивать, причем чем больше тракторов будет приходиться на одного тракториста, тем больше будет время простоя. Если же новые тракторы качественно отличаются от старых, позволяют усовершенствовать технологию обработки земли, то соотношение (13) для производственной функции моделируемой системы  может не выполняться. Кроме того, даже в отсутствие технического прогресса повышение эффективности использования тракторов при росте их количества может быть достигнуто за счет  концентрации производства. Этот эффект бывает особенно заметен в  промышленности.

4) ЧЕТВЕРТОЕ ПРЕДПОЛОЖЕНИЕ. Производственная  функция характеризуется определенной отдачей от расширения масштабов производства. Отдача от расширения масштабов  производства характеризует производственную функцию с точки зрения изменения выпуска продукции при «пропорциональном» изменении затрат ресурсов, которое математически выражается в умножении всех компонент вектора х на положительный скаляр t. Принято говорить, что скалярная функция f(x) является однородной  функцией степени p, если для любого вектора х и любого скаляра t она удовлетворяет соотношению

f(t∙x) = t^p∙f(x). (16)

Математически четвертое предположение состоит в требовании однородности производственной функции. Если p>1, то говорят, что производственная функция характеризуется возрастающей отдачей от расширения масштабов производства; если p=1 — постоянной отдачей (наиболее часто встречающийся случай), а при p<1 — убывающей отдачей. Естественно, что выполняется предположение p>0, ибо в противном случае нарушалось бы  условие (10) во всех точках положительного ортанта и  отсутствовала бы экономическая область.

 ПРИМЕР 5.  Рассмотрим производственную функцию (6). Для нее

f(tx) = (tx)^α= t^α∙x^α= t^α∙f(x).

Таким образом, p=α, т. е. эта функция характеризуется  убывающей отдачей от расширения масштабов производства.

РАЗДЕЛ 3. ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ С ДВУМЯ РЕСУРСАМИ.

 

ЧТО ТАКОЕ ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ (ВЫПУСКА) НЕСКОЛЬКИХ ПЕРЕМЕННЫХ?

 

Производственная функция нескольких переменных - это  функция, независимые переменные х1,..., хn которой принимают  значения объемов затрачиваемых или используемых ресурсов (число  переменных n равно числу ресурсов), а значение функции Y имеет смысл величин объемов выпуска:

 

Y= f(x)=f(x1, ..., xn). (9)

 

В формуле (9) величина у (у≥0) - скалярная, х - векторная величина (x=(x1, ..., xn)), х1, ..., xn

- координаты вектора х.

 

То  есть f(x1, ..., xn) есть числовая  функция нескольких (многих) переменных х1,,..., хn. В связи с этим ПФ f(x1, ..., xn) называют многоресурсной или многофакторной ПФ. Более правильной является такая символика f(х1,... , хn, а), где а - вектор параметров ПФ.

По экономическому смыслу х1≥0, ... , хn≥0, следовательно, областью определения многофакторной ПФ f(x1, ..., xn) является множество n-мерных векторов х, все координаты х1,..., хn которых есть неотрицательные числа.

 

Для отдельного предприятия (фирмы), выпускающего  однородный продукт, ПФ f(x1, ..., xn) может связывать объем выпуска в натуральном или стоимостном выражении) с затратами рабочего времени по различным видам трудовой деятельности, различных видов сырья, комплектующих изделий, энергии, основного капитала  (измеренных обычно в натуральных единицах). ПФ такого типа  характеризуют действующую технологию предприятия (фирмы). При построении ПФ для региона или страны в целом в качестве величины годового выпуска Y (будем обозначать объем выпуска, или дохода, на макро-уровне большой буквой) чаще берут  совокупный продукт (доход) региона или страны, исчисляемый обычно в неизменных, а не в текущих ценах, в качестве ресурсов  рассматривают основной капитал (х1≡K - объем используемого в течение года основного капитала), живой труд (х2≡L - количество единиц  затрачиваемого в течение года живого труда), исчисляемые обычно в стоимостном выражении. Таким образом строят двухфакторную ПФ f(x1, x2) или Y=f(K,L). От двухфакторных ПФ переходят к трехфакторным. В качестве третьего фактора иногда вводят объемы  используемых природных ресурсов. Кроме того, если ПФ строится по данным временных рядов, то в качестве особого фактора роста  производства может быть включен технический прогресс.

 

КАКАЯ ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ НАЗЫВАЕТСЯ СТАТИЧЕСКОЙ?

 

ПФ у = f(x1, x2) называется статической, если ее параметры и ее характеристика f не зависят от времени t, хотя объемы ресурсов и объемы выпуска могут зависеть от времени t, т.е. могут иметь  представление в виде временных рядов: x1(0), x1(1), ..., х1(T); x2(0), x2(1), ..., x2(Т);  у(0), y(1), ..., у(Т); y(t) =f(x1(t),x2(t)). Здесь t- номер года, t =0, 1, ... , Т; t=0 - базовый год временного промежутка, охватывающего годы 1,2, ... Т.

ПРИМЕР 6. Для моделирования отдельного региона или страны в целом (т.е. для решения задач на макроэкономическом, а также и на микроэкономическом уровне) часто используется ПФ вида:

 

у =a0∙x1^a1∙x2^a2, (10)

 

где a0,a1,a2- параметры ПФ. Это положительные  постоянные (часто a1 и а2 таковы, что a1+a2=1).

 

ПФ только что  приведенного вида (10) называется ПФ Кобба-Дугласа (ПФКД) по имени двух американских экономистов, предложивших ее использовать в 1929 г. ПФКД активно применяется для решения разнообразных теоретических и прикладных задач благодаря своей структурной простоте. ПФКД принадлежит к классу так называемых  мультипликативных ПФ (МПФ).

 

В приложениях ПФКД х1≡K равно объему используемого основного капитала (объему используемых  основных фондов - в отечественной терминологии), х2≡L -  затратам живого труда, тогда ПФКД приобретает вид, часто  используемый в литературе:

 

Y = a0∙K^a1∙L^a2 .

 

Графиком ПФ у = a0∙x1^a1∙x2^a2 (где a1+a2=1) в трехмерном  пространстве является двумерная поверхность Γ, эскиз которой представлен на рисунке 5.

 

Рисунок 5. График ПФКД.

 

График Г в рассматриваемом случае есть коническая поверхность, направляющей которой является, например, линия L, а образующими - лучи, выходящие из точки О(0,0,0).

 

Пусть х2=x02>0, тогда  у =a0∙x1^a1∙x02^a2,  и мы получаем вариант ПФ (рисунок 6), аналогичный рассмотренному выше (см. рисунок 3).

 

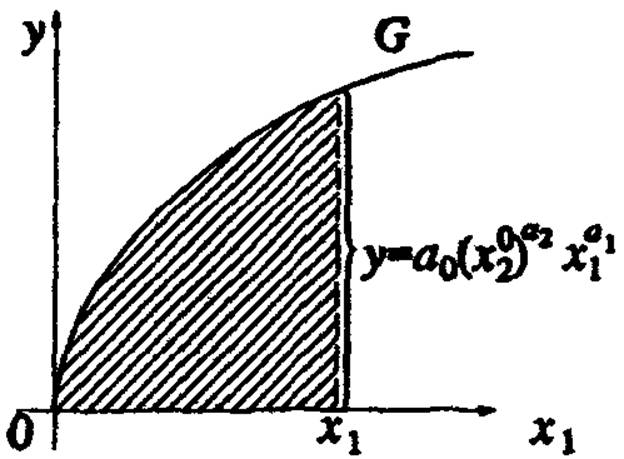
Рисунок 6. График ПФ.

 

Линия G есть пересечение поверхности Г вертикальной плоскостью х2=х02. На рисунке 6 представлен фрагмент рисунка 5, относящийся к линии G. Поведение линии G отражает то обстоятельство, что с ростом затрат первого ресурса объем выпуска у растет, но каждая дополнительная единица первого ресурса обеспечивает все меньший прирост  выпуска у. Это обстоятельство можно прокомментировать следующим образом. Если число работников и их квалификация остаются  неизменными, а число обслуживаемых ими станков (которое уже  достаточно велико) увеличивается, например, в два раза, то это  естественно не приведет к двойному росту объема выпуска. Отметим, что если a1+a2<1, то графиком Г ПФКД является поверхность, которая напоминает выпуклую вверх «горку», крутизна которой падает, если точка (х1, x2) перемещается на «северо-восток» по  плоскости Ох1х2.

 

ПРИМЕР 7. Линейная ПФ (ЛПФ) имеет вид:

 

y=a0+a1∙x1 + a2∙x2

 

(двухфакторная)

 

и

 

y= a0+ a1∙x1 + a2∙x2 +  ... + an∙xn (многофакторная).

 

ЛПФ принадлежит к классу так называемых аддитивных ПФ (АПФ).

 

Переход от мультипликативной ПФ к аддитивной осуществляется с помощью операции логарифмирования. Для двухфакторной  мультипликативной ПФ

 

у =a0∙x1^a1∙x2^a2

 

этот переход имеет вид:

 

ln y = ln a0 +a1∙ln x1 + a2∙ln x2.

 

Заменяя ln y = w, ln x1 = u1, ln x2 = u2, получаем аддитивную ПФ:

 

w = ln a0 + a1∙u1 + a2∙u2.

Выполняя обратный переход, из аддитивной ПФ получим  мультипликативную ПФ.

 

Если сумма показателей степени равна единице (a1+a2=1)  в ПФ Кобба-Дугласа

 

Y = a0∙K^a1∙L^a2  , то ее можно записать в несколько другой форме:

 

Y/L =a0∙K^a1∙L^a2 /L = a0∙K^a1∙L^a2-1 = a0∙K^a1/L^{1- a2} =  a0∙K^a1/L ^a1  .

 

То есть

Y/L = a0∙(K/L) ^a1 

 

Дроби Y/L≡z и K/L≡k называются, соответственно, производительностью труда и капиталовооруженностью труда. Используя новые символы, получим функцию:

 

z = a0∙k ^a1 

 

т.е. из двухфакторной ПФКД получим формально однофакторную ПФКД. В связи с тем, что 0<a1<1, из последней формулы следует, что производительность труда z растет медленнее его  капиталовооруженности. Однако этот вывод справедлив для случая  статической ПФКД в рамках существующих технологии и ресурсов.

Отметим здесь, что дробь Y/K называется производительностью капитала или капиталоотдачей, обратные дроби K/Y и L/Y называются, соответственно,  капиталоемкостью и трудоемкостью выпуска.

 

КАКАЯ ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ НАЗЫВАЕТСЯ ДИНАМИЧЕСКОЙ?

 

ПФ называется динамической, если:

 

1) время t фигурирует в качестве самостоятельной переменной величины (как бы самостоятельного фактора производства),  влияющего на объем выпускаемой продукции;

 

2) параметры ПФ и ее характеристика f зависят от времени t.

 

Отметим, что если параметры ПФ оценивались по данным  временных рядов (объемов ресурсов и выпуска) продолжительностью Т0 лет (т.е. базовый промежуток для оценки параметров имеет  продолжительность T0 лет), то экстраполяционные расчеты по такой ПФ следует проводить не более чем на T0/3  лет вперед (т.е. промежуток экстраполяции должен иметь продолжительность не более чем T0/3 лет).

 

При построении ПФ научно-технический прогресс (НТП) может быть учтен с помощью введения множителя НТП: exp(p∙t), где параметр (число) р (р>0) характеризует темп прироста выпуска под  влиянием НТП:

 

Y(t) =  exp(p∙t) ∙f(x1(t)),x2(t)) (t=0,1, ... ,T).

 

Эта ПФ - простейший пример динамической ПФ; она включает нейтральный, то есть не материализованный ни в одном в одном из факторов, технический прогресс. В более сложных случаях технический  прогресс может воздействовать непосредственно на производительность труда или капиталоотдачу:

 

Y=f(A(t)∙L(t), K(t)) или

 

Y=f(A(t)∙K(t), L(t)).

 

Он называется, соответственно, трудосберегающим или капиталосберегающим НТП.

 

ПРИМЕР 8. Приведем вариант ПФКД с учетом НТП exp(p∙t):

 

у =a0∙ exp(p∙t)∙ x1(t)^a1∙x2(t)^a2.

 

ЧТО ТАКОЕ СПЕЦИФИКАЦИЯ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ?

 

Выделение существенных видов ресурсов (факторов  производства) и выбор аналитической формы функции f(x1,x2) называется  спецификацией ПФ у = f(x1,x2).

 

ЧТО ТАКОЕ ПАРАМЕТРИЗАЦИЯ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ?

Преобразование реальных и экспертных данных в модельную информацию, т.е. расчет численных значений параметров ПФ у = f(x1,x2) на базе статистических данных с помощью регрессионного и корреляционного анализа, называется параметризацией ПФ у = f(x1,x2).

 

ЧТО ТАКОЕ ВЕРИФИКАЦИЯ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ?

 

Проверка истинности (адекватности) ПФ называется ее  верификацией.

 

ЧТО ВЛИЯЕТ НА СПЕЦИФИКАЦИЮ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ?

 

Выбор аналитической формы ПФ у = f(x1,x2) (т.е. спецификация) диктуется прежде всего теоретическими соображениями,  которые должны явно (или даже неявно) учитывать особенности  взаимосвязей между конкретными ресурсами (в случае микроэкономического  уровня) или экономических закономерностей (в случае  макроэкономического уровня), особенности реальных или экспертных данных, преобразуемых в параметры ПФ (т.е. особенности параметризации). На спецификацию и параметризацию в процессе  совершенствования ПФ оказывают влияние результаты верификации ПФ. Отметим здесь, что оценка параметров ПФ обычно проводится с помощью метода наименьших квадратов.

 

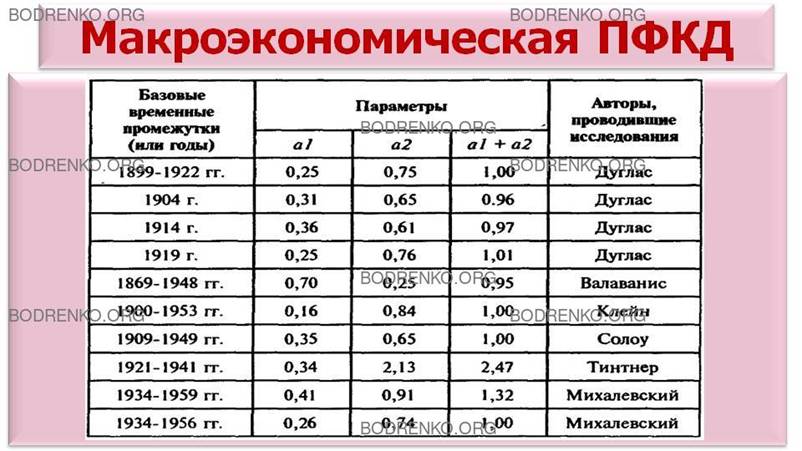
ПРИМЕР 9. Приведем в качестве иллюстрации значения  параметров а1 и а2 макроэкономической ПФ Кобба-Дугласа Y = a0∙K^a1∙L^a2  для экономики США, рассчитанные разными авторами для разных базовых временных промежутков (априори не предполагалось, что обязательно a1 + a2 = 1) (см.: Терехов Л.Л. Производственные  функции. М.: Статистика, 1974, с. 113) (Таблица 1). Параметры разными авторами рассчитывались по разным  методикам, поэтому пестрота картины не является неожиданной.  Обращает на себя внимание, что у всех авторов наблюдается  значительное превышение параметра а2 относительно параметра a2. Также почти у всех авторов сумма a1+а2 оказалась близкой к единице.

 

Таблица1.

 

СВОЙСТВА ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ С ДВУМЯ РЕСУРСАМИ.

 

Сформулируем приведенные выше свойства производственных функций 1) – 4) для функции f(x1,x2) двух переменных x1, x2.

 

Производственная функция f(x1,x2) как формальная  конструкция определена на неотрицательном ортанте  двумерной плоскости, т.е. определена при x1 ≥0, x2≥0. ПФ должна удовлетворять ряду (для каждой конкретной ПФ - своему) свойств:

 

1. f(0,0)=0;

 

1″. f(0,x2)=f(х1, 0)=0;

 

2.  Из условия x(1)≥x(0) (и при этом x(0)≠x(1))  следует условие f(x(1))>f(x(0)), где x(k)=(x1(k), x2(k)), k=0,1;

 

2″. x>0 =>  ∂f(x)/∂xi>0 (i=1,2), х=(х1,x2);

 

3. x>0 =>  ∂2f(x)/∂xi∂xi≤0 (i=1,2), x=(x1,x2);

 

3″.  x>0 =>  ∂2f(x)/∂x1∂x2≥0, x=(x1,x2);

 

4. f(t∙x1,t∙x2) = t^p∙f(x1,x2) .

 

Свойство 1 означает, что без ресурсов нет выпуска. Свойство 1″ означает, что при отсутствии хотя бы одного из ресурсов нет выпуска. Свойство 2 означает, что с ростом затрат хотя бы одного ресурса объем выпуска растет. Свойство 2″ (первая частная производная ∂f(x)/∂xi>0 (i=1,2) ПФ f(x1,x2) положительна) означает, что с ростом затрат одного ресурса при неизменном количестве другого ресурса объем выпуска растет. Упорядоченная пара (х1,x2) чисел х1 и х2 для краткости здесь и далее обозначается символом х, то есть x=(x1,x2).

 

Свойство 3 (вторая частная производная ∂2f(x)/∂xi∂xi≤0 (i=1,2), ПФ f(x1,x2)  неположительна) означает, что с ростом затрат одного (i-го) ресурса при  неизменном количестве другого ресурса величина прироста выпуска на каждую дополнительную единицу i-го ресурса не растет (закон  убывающей эффективности). Свойство 3″ означает, что при росте  одного ресурса предельная эффективность другого ресурса возрастает.

 

Если выполнены условия 3 и 3″, то график Г ПФ есть поверхность, расположенная в неотрицательном октанте х1≥0, x2≥0, y≥0 трехмерного пространства Ox1x2y и выпуклая вверх. Вообще  геометрический образ ПФ должен прежде всего ассоциироваться с выпуклой горкой, крутизна которой убывает, если точка (х1, x2) уходит в  плоскости Ox1x2 на «северо-восток».

 

Свойство 4 означает, что ПФ является однородной функцией (ОФ) степени р>0. При р>1 с ростом масштаба производства в t раз  (число t>1), т.е. с переходом от вектора х к вектору t∙x, объем выпуска возрастает в t^p (>t) раз, т.е. имеем рост эффективности производства от роста масштаба производства. При р<1 имеем падение эффективности производства от роста масштаба  производства. При р=1 имеем постоянную эффективность производства при росте его масштаба (или имеем независимость удельного  выпуска от масштаба производства - в английской терминологии  constant returns to scale).

 

Для ПФКД у =a0∙x1^a1∙x2^a2,  (а1+а2=1) свойства 1-4 выполняются.

 

Для ЛПФ y=a0+a1∙x1 + a2∙x2 , (а0>0, а1>0, а2>0 свойства 1 и 1″(при a0=0) и свойство 4 не выполняются.

 

ЧТО ТАКОЕ ИЗОКВАНТА ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ?

 

Множество (линия) lq уровня q=f(x1,x2) (где 0<q – положительное действительное число) ПФ  y= f(x1,x2) называется изоквантой ПФ. Иными словами, линия lq уровня q - это множество точек, в котором ПФ y= f(x1,x2) постоянна и равна q.

 

Различные наборы (v1,v2) и (w1,w2) затрачиваемых  (используемых) ресурсов, принадлежащие одной и той же изокванте lq уровня q (т.е. q=f(v1,v2)=f(w1,w2)), дают один и тот же объем выпуска q. Изокванта есть линия, расположенная в неотрицательном квадранте x1≥0, x2≥0 двумерной плоскости Ox1x2.

 

ПРИМЕР 10. На рисунке 7 даны эскизы изоквант lq1  и lq2  ПФКД.

 

 

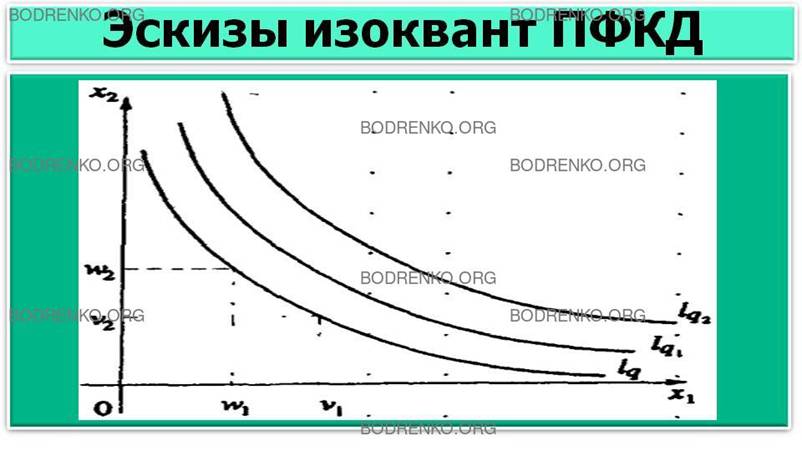
Рисунок 7. Эскизы изоквант ПФКД.

 

Отметим, что изокванта lq2, расположенная «северо-восточнее» изокванты lq1, соответствует большему объему выпуска (т.е. q2>q1).Если объем используемого основного капитала неограниченно растет (т.е. x1≡K→+∞), то, как видно на рисунка 6, затраты труда  неограниченно убывают (т.е. x2≡L→+0). Аналогично, как видно на рисунке 6, если x2≡L→+∞, то x1≡K→+0.

 

На рисунке 8 даны эскизы изоквант lq1  и lq2  (q2>q1) ЛПФ.

 

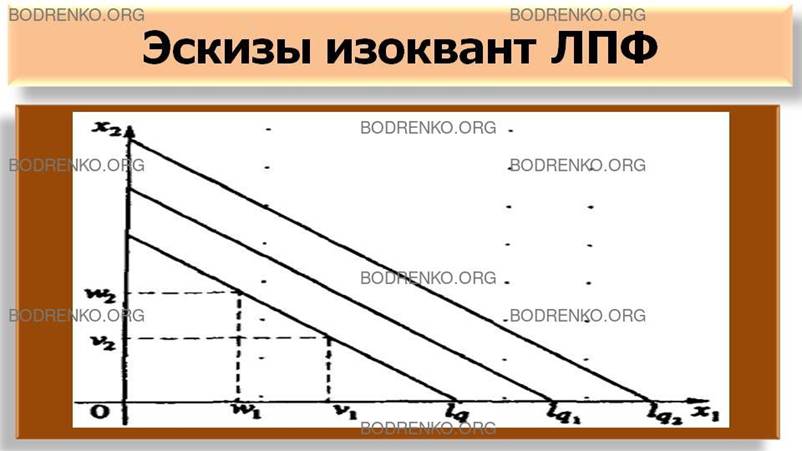
Рисунок 8. Эскизы изоквант ЛПФ.

 

При n=2 для любой ПФ, для которой справедливы все (или часть) свойств 1-4, изокванта (если она не является прямой) есть линия (не обязательно гладкая), которая выпукла к точке О(0,0), т.е. линия, которая похожа на изокванту lq (рисунок 7). Если график Г ПФ похож на выпуклую горку, то естественно, что ее изокванты есть линии, выпуклые к точке О(0,0).

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Замков О.О., Толстопятенко А.В., Черемных Ю.М. Математические методы в экономике: Учебник. 2-е изд. - М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. — 368 с.

 

[2] Лотов А. В. Введение в экономико-математическое моделирование.  –  М.: Наука. Главная редакция физико-математической литературы, 1984.— 392 с.  

[3] Шелобаев С. И. Математические методы и модели в экономике,  финансах, бизнесе: Учеб. пособие для вузов. — М.: ЮНИТИ - ДАНА, 2001. - 367 с.

[4] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).

 

[5] Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш,  Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.:  ЮНИТИ, 1999. - 391 с.