Математические методы исследования экономики

 

Лекция 6

 

Тема лекции 6: «Оптимизационные задачи с ограничениями»

Разделы лекции:

 

1. Задачи оптимального программирования.

2. Постановка задач математического программирования.

3. Примеры задач оптимального программиро­вания.

РАЗДЕЛ 1.  ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ.

 

Выбор оптимального управленческого по­ведения в конкретной производственной ситуации связан с проведением с позиций системности и оптимальности эко­номико-математического моделирования и решением задачи оптимального программирования.

Задачи оптимального программирования в наиболее об­щем виде классифицируют по следующим признакам.

КАК КЛАССИФИЦИРУЮТ ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ ПО ХАРАКТЕРУ ВЗАИМОСВЯЗИ МЕЖДУ ПЕРЕМЕННЫМИ?

 

1. По характеру взаимосвязи между переменными задачи оптимального программирования разбивают на следующие группы:

 

а) линейные,

б) нелинейные.

В случае а) все функциональные связи в системе ограни­чений и функция цели — линейные функции; наличие не­линейности хотя бы в одном из упомянутых элементов приводит к случаю б).

КАК КЛАССИФИЦИРУЮТ ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ ПО ХАРАКТЕРУ ИЗМЕНЕНИЯ ПЕРЕМЕННЫХ?

 

2. По характеру изменения перемен­ных задачи оптимального программирования разбивают на следующие классы:

а) непрерывные,

б) дискретные.

 

В случае а) значения каждой из управляющих перемен­ных могут заполнять сплошь некоторую область действи­тельных чисел; в случае б) все или хотя бы одна переменная могут принимать только целочисленные значения.

КАК КЛАССИФИЦИРУЮТ ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ ПО УЧЕТУ ФАКТОРОВ ВРЕМЕНИ?

 

3. По учету фактора времени задачи оптимального программирования разбивают на следующие классы:

а) статические,

б) динамические.

В задачах а) моделирование и принятие решений осуще­ствляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение. В случае б) такое предположение достаточно аргументированно не может быть и необходимо учитывать фактор времени.

КАК КЛАССИФИЦИРУЮТ ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ ПО НАЛИЧИЮ ИНФОРМАЦИИ О ПЕРЕМЕННЫХ?

 

4. По наличию информации о переменных задачи оптимального программирования разбивают на следующие три класса:

а) задачи в условиях полной определенности (детерми­нированные),

б) задачи в условиях неполной информации,

в) задачи в условиях неопределенности.

В задачах б) отдельные элементы являются вероятност­ными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения. В случае в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.

КАК КЛАССИФИЦИРУЮТ ЗАДАЧИ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ ПО ЧИСЛУ КРИТЕРИЕВ ОЦЕНКИ АЛЬТЕРНАТИВ?

 

5. По числу критериев оценки альтер­натив задачи оптимального программирования разбивают на следующие классы:

а) простые, однокритериальные задачи,

б) сложные, многокритериальные задачи.

В задачах а) экономически приемлемо использование од­ного критерия оптимальности или удается специальными процедурами (например, «взвешиванием приоритетов») све­сти многокритериальный поиск к однокритериальному.

КАК МОЖНО ГРУППИРОВАТЬ ЗАДАЧИ И МЕТОДЫ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ ПО НАИБОЛЕЕ ОБЩИМ ПРИЗНАКАМ КЛАССИФИКАЦИИ?

 

Сочетание признаков 1—5 позволяет группировать (клас­сифицировать) в самом общем виде задачи и методы опти­мального программирования. Например, сочетание общих признаков 1а)2а)3а)4а)5а) приводит к  задачам  и методам линейного программирования. Сочетание общих признаков 1б)2а)3а)4а)5а) характеризует задачи и методы нелинейного программирования. Сочетание общих признаков 1а)2б)3а)4а)5а) выделяет задачи и методы целочисленного (дис­кретного) линейного программирования и т.д.

Выбору метода решения конкретной задачи оптимально­го программирования предшествует ее классификация, т.е. отнесение к одному из классов оптимизационных задач, на­чиная с приведенных самых общих признаков (например, задача дискретного линейного программирования с булевыми переменными).

Развитие и совершенствование методов решения задач оптимального программирования идет от случаев типа а) к случаям типа б), в).

КАКОЙ КЛАСС ЗАДАЧ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ НАИБОЛЕЕ ИЗУЧЕН?

 

В настоящее время множество задач планирования и управле­ния, а также большой объем частных прикладных задач решаются методами математического программирования. Ф наиболее развитыми в области решения оптимизационных задач являются методы линейного программи­рования. Эти методы позволяют описать с достаточной точнос­тью широкий круг задач, среди которых отметим следующие.  Планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организа­ция рациональных перевозок товаров (транспортная задача); распределение работников по должностям (задача о назна­чении); организация рациональных закупок продуктов питания (задача о диете);  распределение ресурсов; планирование капита­ловложений; оптимизация межотраслевых связей; замена торго­вого оборудования; определение оптимального ассортимента то­варов в условиях ограниченной площади; установление рацио­нального режима работы. В задачах линейного программирования критерий эффектив­ности и функции в системе ограничений линейны. Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования. Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается че­рез уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования. Наиболее изучены задачи линейного программирования, для которых разработан универсальный метод решения — метод последовательного улучшения плана (симплекс-метод), т.е. любая задача линейного программирования решается (реализуется) этим методом.  Во многих экономических моделях зависимости между посто­янными и переменными факторами можно считать линейными. Именно такие задачи в дальнейшем рассматриваются на этой лекции.

 

РАЗДЕЛ 2. ПОСТАНОВКА ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ.

1. ПЛАНИРОВАНИЕ ТОВАРООБОРОТА.

 

Коммерческое предприятие реализует товары нескольких групп  Aj (j = 1,…, n). Для реализации этих товаров используются ресурсы с ограниченным объемом:

 

b1 — рабочее время (чел.-ч);

 

b2  - площадь залов (м2);

 

b3 - издержки обращения (руб.).

 

Известны нормы расхода каждого вида ресурса на реализацию единицы j-й группы товара —

aij  (i= 1,2,3; j =1,…, n). Доход от продажи в расчете на единицу товара составляет cj. Необходимо составить оптимальный план товарооборота по критерию максимума дохода (или по другому критерию — мини­мум издержек обращения).

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

Известно, что величина дохода линейно связана с объемом продажи товаров xj. В связи с этим целевую функцию можно за­писать в виде

F(X) = c1x1 + с2х2 + ... + cnxn => max.

Очевидно, что объем продажи товаров не может быть отрица­тельной величиной. Поэтому хj≥0 , j=1, …, n. Учитывая нормы затрат ресурсов и их объемы, запишем огра­ничения в виде системы:

 

Решение задачи можно получить с помощью симплексного метода.

 

2. ПРОИЗВОДСТВЕННАЯ ЗАДАЧА.

Предприятие изготавливает несколько видов продукции, рас­ходуя на это изготовление различные виды сырья. Запасы сырья ограничены. Доход, получаемый от реализации каждого вида продукции, различен. Необходимо составить такой план выпуска продукции, при котором доход предприятия был бы максималь­ным.

 

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

Для изготовления n видов продукции Рj(j=1, …, n) использует­ся m видов сырья Si (i=1, …, m). Запасы сырья составляют bi, i=1, …, m. Нормативы затрат сы­рья на изготовление единицы продукции составляют aij. Доход, получаемый от реализации единицы продукции j-го вида, состав­ляет Dj, j=1, …, n. Необходимо составить такой план выпуска продукции, при котором доход от ее реализации будет максимальным.

Обозначим xj количество единиц продукции j-го вида (j=1, …, n), запланированных к производству. Тогда целевая функ­ция будет иметь вид:

 

F(X)=∑{j=1,…, n} Dj∙xj  => max.

Для изготовления всей продукции потребуется

∑{j=1, …, n}aij∙xj

 

единиц сырья i-го  вида. Поскольку его количество ограничено вели­чиной bi, получаем неравенство

∑{j=1, …, n}aij∙xj≤bi; i=1, …, m.

 

Учитывая нормативы затрат и ограничения на ресурсы, запи­шем систему неравенств:

 

3. ФОРМИРОВАНИЕ РАЦИОНАЛЬНЫХ СМЕСЕЙ.

В коммерческой деятельности возникают задачи, связанные с осуществлением рациональных закупок продуктов, обеспечива­ющих необходимый рацион питания для поддержания нормаль­ной жизнедеятельности человека, или формирование диетичес­кого питания в больницах, или задачи составления кормовых смесей на животноводческих фермах. Задачи о рациональном питании решаются в условиях огра­ниченного ассортимента, товарных запасов, стоимости, суточ­ных норм потребления питательных веществ и их содержания в продуктах. Причем из всех возможных вариантов необходимо выбрать самый дешевый.

 

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

 

Допустим, имеется набор продуктов: мясо, рыба, молоко, са­хар, яйца, картофель, овощи, фрукты, хлеб, мука  и т.д.,  по ценам соответственно c1, c2, …, cj, …, cn, причем запасы этих продуктов огра­ничены, соответственно, величинами: а1, а2,..., аj ..., аn. Содержание питательных веществ — белков, жиров, углево­дов, витаминов и минеральных солей — в 1 кг каждого продукта известны и составляют соответственно qij (i = 1, …, m; j=1, …, m). Кроме того, известны нормы суточной потребности человека в каждом питательном веществе: b1, b2,..., bi,..., bm. Необходимо определить количество закупаемых продуктов x1, x2, …, xj, …, xn,  которое обеспечит потребность в питательных веществах каждого вида и будет иметь минимальную стоимость.

Кроме того, количество каждого продукта в рационе не может быть величиной отрицательной, а размер закупок ограничен за­пасами. Тогда имеем следующую систему неравенств:

 

0≤x1≤a1, 0≤x2≤a2, …, 0≤xi≤ai, …,  0≤xn≤an,

Так как содержание питательных веществ в рационе должно быть не менее b1, b2,..., bi,..., bm, то получим систему линейных ограниче­ний:

 

 

Общая стоимость рациона запишется в виде линейной целе­вой функции:

F(X)=c1x1+c2x2+ …, cjxj+ …, cnxn => min.

 

4. ПЕРЕВОЗКА ГРУЗОВ.

В современных условиях большие транспортные расходы свя­заны с простоями в ожидании обслуживания на погрузочно-разгрузочных работах, порожними пробегами, встречными и нера­циональными перевозками, затратами на бензин, техническое обслуживание и заработную плату водителей. В связи с этим не­ обходимо решать задачи оптимального планирования перевозок грузов в коммерческой деятельности из пунктов отправления (баз, станций, фабрик, совхозов, заводов) в пункты назначения (магазины, склады) методами, позволяющими оптимизировать план по какому-либо экономическому показателю, например финансовых затрат или времени на перевозку грузов.

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

 

Имеется m  пунктов отправления (поставщиков) грузов: A1, A2, …, Ai, …, Am, на которых сосредоточены запасы какого-либо однородного гру­за в объемах соответственно: a1, a2, …, ai, …, am.  Величины аi определяют максимально возможные размеры вывоза груза с пунктов отправления. Суммарный запас груза поставщиков составляет ∑ai. Кроме того, имеется n пунктов назначения: B1, B2, …, Bj, …, Bn,  которые подали заявки на поставку грузов в объемах соответст­венно: b1, b2, …, bj, …, bn.

 

Суммарная величина заявок составляет ∑ bj. Стоимость перевозки одной единицы груза от поставщика Аi к потребителю Bj обозначим через cij (транспортный тариф), образующих матрицу транспортных издержек С=||cij||. В качестве критерия оптимальности выбираем суммарные издержки по перевозке грузов.

Тогда транспортная задача формулируется следующим обра­зом: необходимо составить оптимальный план, т.е. найти такие значения объема перевозок грузов || xij || от поставщиков Аi к по­требителям Bj, чтобы вывести все грузы от поставщиков; удовле­творить заявки каждого потребителя и обеспечить минимальные транспортные расходы на перевозку груза.

Все исходные данные транспортной задачи можно записать в виде таблицы 1, которая называется транспортной.

 

Таблица 1.

 

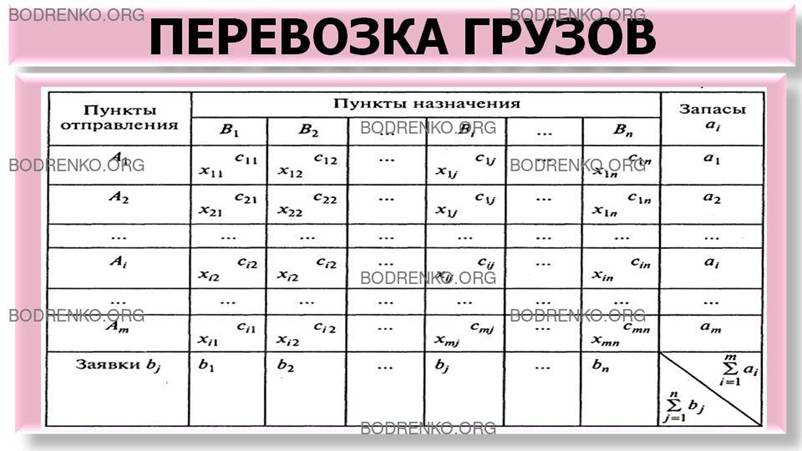
Задача заключается в определении плана перевозок - матри­цы X=||xij||(i=1, …, m; j=1, …, n), которая удовлетворяет следующим усло­виям:

И обеспечивает минимальное значение целевой функции

 

В таком виде экономико-математическая постановка транс­портной задачи считается законченной. Транспортная задача может быть решена на компьютере, по­скольку математические методы, как правило, реализованы в ви­де специальных программ.

5. ЗАДАЧА О НАЗНАЧЕНИЯХ.

 В коммерческой сфере возникают задачи, связанные с необ­ходимостью выбора такого варианта распределения ресурсов: трудовых, товарных, финансовых, энергетических, материальных, природных и других по некоторым объектам - магазинам, городам, предприятиям, цехам и т.п., который обеспечил бы ми­нимальные затраты денег, времени или максимальные прибыль и доход и минимальные издержки. Так, например, всегда актуальной является проблема форми­рования трудового коллектива. Известно, что один и тот же работник может выполнять раз­личные функции с разной производительностью в зависимости от опыта работы, квалификации, индивидуальных особенностей. Поэтому возникает задача о назначениях, предполагающая такое распределение работников по должностям, при котором произ­водительность труда в коллективе была бы максимальной.

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

 

На коммерческом предприятии имеется m работников: A1, A2, …, Ai, …, Am,   каждый из которых должен выполнять одну Bj из имеющихся n видов работ: B1, B2, …, Bj, …, Bn. Для каждого работника Аi на рабочем месте Bj рассчитывается производительность труда cij. Необходимо определить, кого и на какую работу следует назначить, чтобы добиться максимальной или минимальной стоимости назначения суммарной производи­тельности при условии, что каждый работник может быть назна­чен только на одну работу.

Пусть количество работников  равно количеству работ, то есть m=n. Обозначим xij назначение i-го работника на j-ю работу. Коли­чество работников m равно количеству работ, поэтому xij может принимать только два целочисленных значения: 1, если i-й ра­ботник назначен на выполнение j-й работы; 0, если не назначен.

При назначении i-го работника на j-ю работу производитель­ность или стоимость назначения равна cij ∙xij. Необходимо постро­ить квадратную матрицу распределения по должностям X, кото­рая обеспечивает максимальное или минимальное значение ли­нейной функции цели

 

при ограничениях

 

Задача о назначениях является частным случаем транспорт­ной задачи, поэтому для ее решения можно воспользоваться лю­бым алгоритмом линейного программирования, однако более эффективным является венгерский метод.

6. ФОРМИРОВАНИЕ ТОРГОВОЙ СЕТИ.

В регионе расположены населенные пункты, численность жителей которых, а также расстояние между ними, стоимость по­ездок известны. Кроме того, задано множество типовых проектов предприятий общественного питания. Необходимо найти опти­мальный план размещения предприятий общественного питания в регионе, обеспечивающий минимальные приведенные затраты на их строительство, эксплуатацию и на поездки населения меж­ду населенными пунктами.

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

 

Введем обозначения показателей, которые относятся к содер­жанию задачи:

n - количество населенных пунктов;

j — номер населенного пункта; j =1,…, n;

Nj - численность населения j-го населенного пункта;

rij - расстояние между пунктами i и j;

i -  индекс пункта размещения предприятия общественного пи­тания (i=1, …, m);

Qj — количество типовых вариантов предприятий для j-го пункта;

q — номер типового предприятия общественного питания, q= l,…, Q;

Bj — спрос населения в j-м населенном пункте на продукцию об­щественного питания;

b — норма обеспеченности продукцией общественного питания одного человека;

Rдоп — максимально допустимый радиус передвижения населения;

Xij  — численность населения j-го пункта, обслуживаемого предпри­ятием i-го пункта;

xiq — типовой вариант q предприятия общественного питания i-го пункта;

сiq — текущие затраты для хiq;

рiq — единовременные затраты для хiq;

cij — затраты на поездку одного жителя из пункта i в пункт j;

Ен — нормативный коэффициент эффективности капитальных вложений.

В качестве критерия оптимальности принимаем приведенные затраты С на строительство, эксплуатацию и на поездки населе­ния.

 

Тогда формальная запись задачи представляет такой вид: найти такие типовые варианты xiq предприятий общественного питания для каждого i-го пункта и xij численности населения j-го пункта, обслуживаемого предприятиями i-го пункта, обеспечива­ющие минимум затрат в соответствии с целевой функцией вида

 

при следующих условиях-ограничениях:

1) предложение продукции общественного питания, предостав­ляемое населению района предприятиями общественного питания j-го пункта, должно соответствовать мощности предприятия:

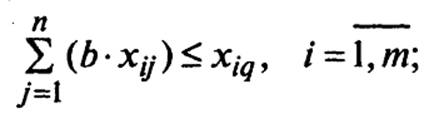
2) потребность населения j-го пункта в продукции, обеспечива­емой предприятиями района, должна быть удовлетворена:

 

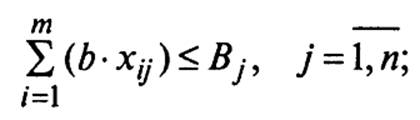
3) расстояние от j-го пункта расселения до i-го пункта размеще­ния предприятия не должно превышать допустимого радиуса об­служивания rij≤Rдоп. Кроме того, существуют ограничения на пе­ременные xij≥0.

Решение этой задачи проводят путем последовательного под­бора типовых мощностей предприятий торговли или обществен­ного питания xij в модели и определении величин затрат для каж­дого варианта.

 

7. ПОСТРОЕНИЕ КОЛЬЦЕВЫХ МАРШРУТОВ.

Коммерческая деятельность обычно связана с командировка­ми, поездками по городам для заключения сделок. Расстояния между любой парой множества из n городов известны и составля­ют aij (i=1,…, m; j=1, …, n, i ≠j). Если прямого маршрута между горо­дами i и j не существует, то допускают, что аij=∞. Коммерсант, выезжая из какого-либо города, должен посе­тить все города, побывав в каждом из них один и только один раз, и вернуться в исходный город. Необходимо определить такую по­следовательность объезда городов, при которой длина маршрута была бы наименьшей.

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

 

Экономико-математическая постановка этой задачи может быть представлена как задача целочисленного линейного про­граммирования. Переменные определим следующим образом:  xij=1, если коммивояжер переезжает из города i в город j (i=1,…, m; j=1, …, n, i ≠j); в противном случае хij=0.

Задача заключается в определении матрицы целых неотрица­тельных значений переменных xij, минимизирующих целевую функцию вида

 

при ограничениях:

1) для въезда в город j только один раз:

 

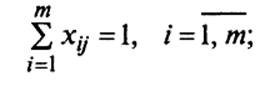
2) для выезда из города i только один раз:

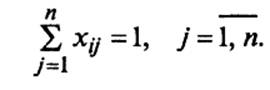
В такой постановке задача коммивояжера представляет собой задачу целочисленного линейного программирования. Действи­тельно, условия аij=∞ исключают в оптимальном решении зна­чения xij=1 как не имеющие смысла, а ограничения требуют:

1) чтобы маршрут включал только один въезд в каждый город;

2) чтобы маршрут включал лишь один выезд из каждого города, а целевая функция включала длину маршрута коммивояжера;

3) чтобы маршрут образовывал контур, проходящий через все го­рода. Таким образом, формируется экономный вариант маршрута в виде кольца.

Решение этой задачи строится, например, методом ветвей и границ целочисленного программирования.

 

8. ВЫБОР ПОРТФЕЛЯ ЦЕННЫХ БУМАГ.

При инвестировании денежных средств в ценные бумаги: ак­ции, облигации, валюты, векселя, возникают задачи оптимиза­ции. Обычно денежные средства вкладывают в несколько видов ценных бумаг, которые образуют портфель активов. Доходность портфеля характеризуется средневзвешенной до­ходностью его составляющих, которая для портфеля из двух ак­тивов рассчитывается следующим образом:

Д=Wa∙Дa + Wb∙Дb

 

где Д — общая доходность портфеля; Wa - удельный вес актива А; Дa - доходность актива А; Wb, — удельный вес актива В; Дb - доходность актива В.

Будущая стоимость ценных бумаг (в отличие от текущей) не определена и  зависит от большого количества различных факто­ров. Количественная мера этой неопределенности называется риском. При этом методы линейного программирования можно использовать для контроля систематического риска при форми­ровании портфеля активов.

Допустим, имеется множество активов Ai (i=1, …, m), а ожидае­мые доходы для них соответственно равны Дi. Доли каждого из этих активов в портфеле соответственно равны Wi и являются пе­ременными, которые могут корректироваться. Риск портфеля R определяется как средневзвешенная величина рисков активов гi.

Цель процедуры оптимизации заключается в максимизации дохода по портфелю при заданном ограничении уровня риска портфеля.

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

Определим оптимальные пропорции (веса) каждого из акти­вов, которые приведут к максимальному ожидаемому доходу при условии заданного максимального уровня риска. Эта задача мо­жет быть сформулирована следующим образом. Ограничения следующие.

Первое ограничение связано с тем, что:

1) риск R портфеля не должен превышать Rдоп;

2) в каждый актив обязательно должны быть проведены поло­жительные инвестиции;

3) все средства должны быть полностью инвестированы. Та­ким образом, ограничения имеют следующий вид: ∑Wi∙ri≤Rдоп, где все активы могут иметь только неотрицательные веса 0≤Wi≤1; причем ∑Wi=1,  поскольку средства должны быть полностью инвестированы.

Все ограничения линейны и представлены в виде равенств и неравенств. Целевая функция имеет вид:

Д=∑Wi∙Дi  => max.

Поскольку доход по каждому активу предопределен, то в це­левой функции могут изменяться только веса.

 

РАЗДЕЛ 3. ПРИМЕРЫ ЗАДАЧ ОПТИМАЛЬНОГО ПРОГРАММИРОВАНИЯ.  

 

Рассмотрим конкретные примеры задач оптимального программиро­вания.

ПРИМЕР 1.

 

Построить экономико-математическую модель оп­ределения структуры выпуска первых и вторых блюд предприя­тия общественного питания при заданном квартальном плане то­варооборота 270 тыс. руб. и получении максимального дохода на основе данных, приведенных в таблице 2.

 

Таблица 2.

 

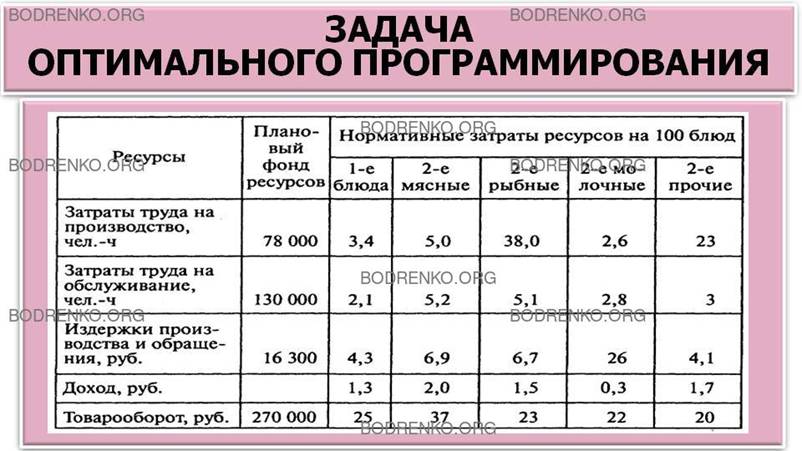
Экономико-математическая модель задачи имеет следующий вид.

Найти такое количество выпускаемых блюд — вектор X=(x1,x2, x3, x4, x5), которое при заданных ограничениях по использованию ресурсов, представленных в виде следующей системы линейных неравенств:

обеспечивает максимум дохода в соответствии с целевой функ­цией

F(X)=1,3x1+2x2+1,5x3+0,3x4+1,7x5 => max.

 

ПРИМЕР 2.

Построить экономико-математическую модель оп­ределения структуры выпуска блюд на предприятии обществен­ного питания, обеспечивающую максимальный доход на основе заданных объемов, ресурсов и нормативов затрат продуктов на первые и вторые блюда, представленных в таблице 3.

Таблица 3.

 

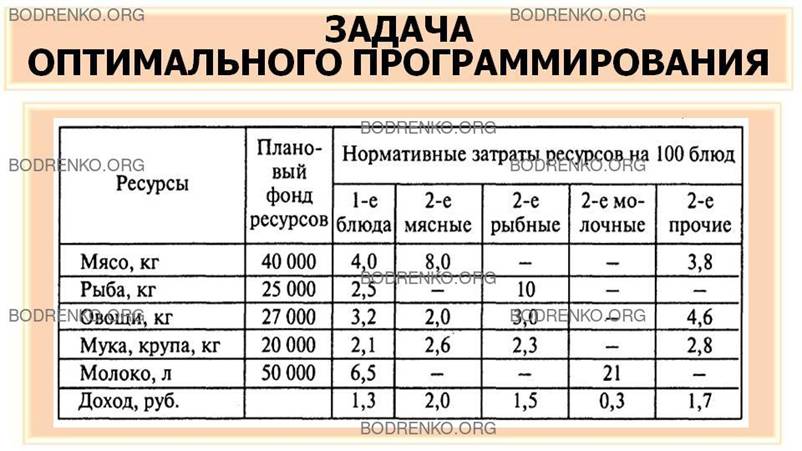
Экономико-математическая модель задачи имеет следующий вид.

Найти такое количество выпускаемых блюд - арифметичес­кий вектор  X=(x1,x2, x3, x4, x5), который при заданных ограничениях

 

обеспечивает максимум дохода в соответствии с целевой функ­цией

 

F(X)=1,3x1+2x2+1,5x3+0,3x4+1,7x5 => max.

 

ПРИМЕР 3 (КОММЕРЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ ПРЕДПРИЯТИЯ).

Коммерческому отделу поручили проанализировать совмест­ную деятельность подразделений фабрики по изготовлению и продаже двух видов краски для внутренних (В) и наружных (Н) работ, которая поступает в продажу по цене 3 тыс. руб. и 2 тыс. руб. за 1 т. Для производства красок используют два вида сырья А и В, максимально возможные суточные запасы которых состав­ляют 3 т и 4 т. Расходы сырья на производство 1 т красок приве­дены в таблице 4.

 

Таблица 4.

 

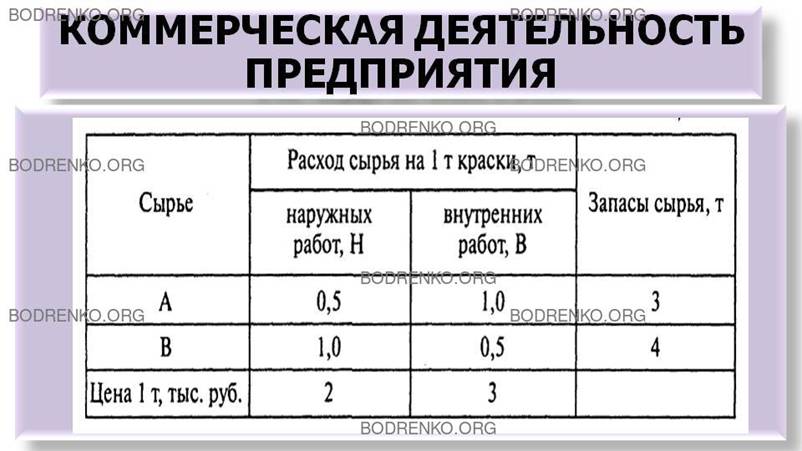
Изучение конъюнктуры спроса на рынке сбыта показало, что суточный спрос на краску для внутренних работ никогда не пре­вышал спроса на краску для наружных работ более чем на 1,5 т, а спрос на краску для внутренних работ никогда не превышал 2 т в сутки. Какое количество краски каждого вида необходимо произ­водить, чтобы доход от ее реализации был максимальным? Кроме того, известно, что план фабрики должен предусмот­реть обязательный выпуск красок, производство которых не опу­скалось ниже 0,25 т, для красок для наружных работ и ниже 0,5 т — для красок для внутренних работ.

ПОСТРОЕНИЕ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАДАЧИ.

Поскольку в задаче необходимо определить объемы произ­водства для продажи краски, то суточные объемы производства красок для наружных и внутренних работ обозначим хн и хв тонн соответственно. Критерием, по которому определяется степень достижения поставленной цели, является доход от продажи краски, который должен быть максимально возможным. На этом основании целе­вую функцию можно записать таким образом:

F(X) = (2xн+ Зхв) => max.

Решение любой задачи осуществляется в рамках ограничен­ных ресурсов. В данном случае необходимо учесть ограничения на расход сырья, запасы которого на фабрике не бесконечны,  также ограничения на спрос краски. Математически эти ограничения можно записать следующим образом:

Объемы производства и соответственно продажи краски не могут принимать отрицательных значений. В связи с этим необходимо записать тривиальное условие неотрицательности пере­менных: хн≥0; xв≥0.

Таким образом, в целом экономико-математическую модель задачи можно представить в таком виде. Определить суточные объемы производства красок — вектор X=(xн, xв), который при заданных условиях-ограничениях

 

обеспечивает максимальный доход от продажи краски в соответ­ствии с целевой функцией

F(X) = (2xн +3xв) =>  max.

Полученная модель является задачей линейного программи­рования, так как все входящие в нее функции линейны. Решение задачи такого класса возможно с использованием либо геометри­ческого, либо алгебраического симплексного методов.

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Замков О.О., Толстопятенко А.В., Черемных Ю.М. Математические методы в экономике: Учебник. 2-е изд. - М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. — 368 с.

 

[2] Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

[3] Шелобаев С. И. Математические методы и модели в экономике,  финансах, бизнесе: Учеб. пособие для вузов. — М.: ЮНИТИ - ДАНА, 2001. - 367 с.

[4] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).

 

[5] Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш,  Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.:  ЮНИТИ, 1999. - 391 с.