Математические методы исследования экономики. Абсолютные и относительные величины в экономическом анализе. Соотношения между суммарными, средними и маржинальными (предельными) величинами. Функции суммарного, среднего и предельного дохода и издержек. Функция спроса. Совершенная конкуренция. Предельные издержки. Предельная выручка. Предельная полезность. Предельный продукт труда. Кривая спроса. Темп роста. Средние издержки. Экономический анализ
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Математические методы исследования
экономики
Лекция 5
Тема лекции 5: «Соотношения между суммарными, средними и предельными
величинами в экономике»

Разделы лекции:
1. Абсолютные и относительные величины
в экономическом анализе.
2. Соотношения между суммарными, средними и маржинальными (предельными) величинами.
3. Функции суммарного, среднего и
предельного дохода и издержек.

РАЗДЕЛ 1. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ В ЭКОНОМИЧЕСКОМ АНАЛИЗЕ.
Все экономические показатели можно, с
известной долей условности,
разделить на абсолютные и относительные. Первые выражаются в каких-либо объемных или денежных единицах и
могут быть либо потоковыми (то есть величина за определенный период),
либо запасовыми (то есть величина на определенную дату). Вторые, относительные, показатели представляют собой отношения абсолютных (или других относительных) показателей, то есть
количество единиц одного показателя на одну единицу другого.
Относительными показателями являются не
только соотношения разных показателей в
один и тот же момент времени, но и одного и того же – в разные
моменты; это - темпы роста данного показателя. В экономическом анализе и принятии решений в одних случаях
важны абсолютные показатели (например, общий объем прибыли), в других - относительные (например, доход надушу населения). Как
правило, для комплексного анализа экономической ситуации, для выбора наилучшего решения важны как
абсолютные, так и относительные показатели. Пусть, например, фирма решает вопрос о необходимом масштабе расширения (или сокращения) объема производства. Ее, естественно, интересует
(абсолютный) показатель
прибыли, являющийся разностью двух других таких показателей - выручки и издержек. Но при решении
поставленной задачи максимизации прибыли фирма широко использует два типа относительных показателей: это средние и предельные величины
(прибыли,
выручки, издержек). Средняя величина в данном случае показывает величину соответствующего показателя в расчете на
единицу выпуска, предельная - прирост соответствующего показателя в расчете на единицу прироста выпуска. Так, если средняя
выручка превышает
средние издержки, то фирма получает прибыль и производить продукцию выгодно. Если при этом предельная
выручка превышает
предельные издержки, то фирме выгодно расширять производство, увеличивая объем прибыли. Соответственно, если
средние издержки превышают среднюю выручку, то фирма терпит убытки, а
если предельные издержки превышают предельную выручку, то объем
производства нужно сократить. Далее мы рассмотрим формально роль абсолютных (суммарных) и относительных
(средних и предельных величин) в экономическом анализе, а также
свойства и соотношения этих величин.
ОПРЕДЕЛЕНИЕ И ГЕОМЕТРИЧЕСКАЯ
ИНТЕРПРЕТАЦИЯ СУММАРНЫХ,
СРЕДНИХ И ПРЕДЕЛЬНЫХ ВЕЛИЧИН.
СУММАРНАЯ ВЕЛИЧИНА (F(x)). Под суммарной величиной мы будем понимать
любую функцию независимой переменной F(x). Как правило, в
экономике под суммарными понимаются абсолютные величины, но, вообще говоря, формальное понятие суммарной величины является относительным (то есть любая величина
может рассматриваться
как суммарная по отношению к другим, своим предельным и
средним величинам). В экономике в роли суммарных величин выступают: доход (выручка) или
издержки как функции объема выпуска (R(Q) или C(Q)), объем выпуска как функция от количества
переменного ресурса, например, труда (функция Q(L)), полезность как функция количества потребляемого блага (функция U(x)) и другие экономические показатели. Любая из
перечисленных функций может быть
задана в виде формулы, например, F(x)= ax∙x - bx, графика, например,
показанного на рисунке 1, и т.д.
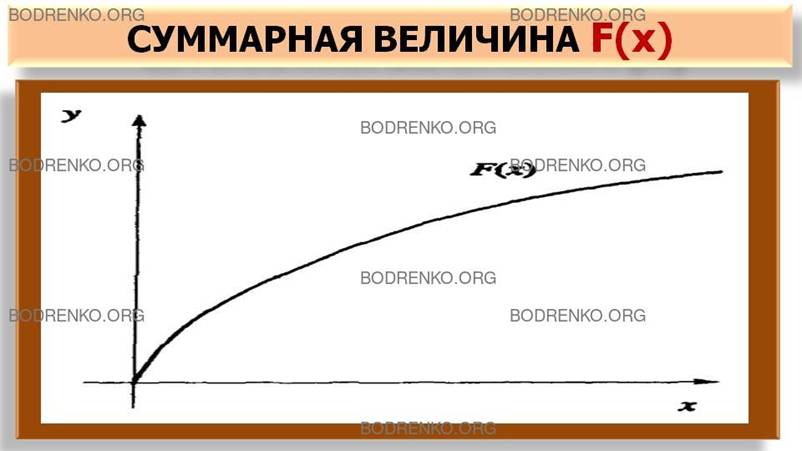
Рисунок 1. График функции y = F(x).
СРЕДНЯЯ ВЕЛИЧИНА (AF(x)) определяется как отношение суммарной
величины к независимой переменной:
AF(x)= F(x)/x.
Буква А - сокращение от Average (средняя).
Средняя величина может обозначаться также
AQ = AQ(L).
ПРИМЕРЫ СРЕДНИХ ВЕЛИЧИН В ЭКОНОМИКЕ:
среднедушевой объем потребления,
средняя фондоотдача, средняя выручка (доход) AR = R(Q)/Q, средние
издержки: AC=C(Q)/Q, средний продукт
труда AQ(L) = Q(L)/L, и т.д.

Средняя величина, как функция независимой переменной, также может задаваться в формульном или графическом виде.
МАРЖИНАЛЬНАЯ (ПРЕДЕЛЬНАЯ) ВЕЛИЧИНА (MF(x)) определяется как производная
суммарной величины F(x) по независимой переменной х:
MF(x)
= F′(x) = lim{Δx→0}ΔF(x)/Δx в случае, когда независимая переменная меняется непрерывно. Если суммарная
величина меняется дискретно, то
под маржинальной (предельной) величиной понимают отношение изменения ΔF(x) суммарной величины F(x) к вызвавшему это
изменение изменению (приращению) Δх независимой переменной х: MF(x) = ΔF(x)/Δх. В этом случае маржинальную
(предельную) величину можно интерпретировать как изменение суммарной величины, вызванное увеличением независимой переменной на
единицу (в соответствующем масштабе).
ПРИМЕРЫ ПРЕДЕЛЬНЫХ ВЕЛИЧИН В ЭКОНОМИКЕ:
предельная выручка (доход) MR = R′(Q) или ΔR/ΔQ;
предельные издержки МС= C′(Q) или ΔС/ΔQ;
предельный продукт труда MQ(L) = Q′(L) или ΔQ/ΔL;
предельная полезность MU =U′(x) или ΔU/Δx; и т.д.

Предельная величина, как и все
предыдущие, может задаваться формулой или
в графическом виде.
РАЗДЕЛ 2. СООТНОШЕНИЯ МЕЖДУ СУММАРНЫМИ, СРЕДНИМИ И МАРЖИНАЛЬНЫМИ (ПРЕДЕЛЬНЫМИ) ВЕЛИЧИНАМИ.
Встречаясь с этими величинами в
экономике, часто приходится использовать соотношения между ними (например, между суммарными, средними и предельными издержками) и решать
задачи на нахождение по одной из этих величин двух других (например, среднего и предельного дохода по суммарному доходу). Рассмотрим задачи нахождения по
одной из этих величин двух других.
ФОРМАЛЬНЫЙ И ГРАФИЧЕСКИЙ АНАЛИЗ.
НАХОЖДЕНИЕ СРЕДНЕЙ ВЕЛИЧИНЫ ПО
СУММАРНОЙ. Формальный и графический анализ. Формально, эта задача решается с
помощью определения средней величины: AF(x) = F(x)/x. Например, если F(х) = x(а - x∙b∙x), то AF(x) = а - bх∙x.

Для графического решения этой задачи (когда суммарная величина задана
в виде графика)
необходимо
провести вектор, соединяющий начало координат с точкой графика функции,
имеющей координаты (x,F(x)). Тангенс угла наклона этого вектора, равный отношению противолежащего (углу β) катета прямоугольного
треугольника F(x) к прилежащему катету х:
tgβ = F(x)/x, будет (по определению) численно равен средней
величине AF(x) = tgβ(x) при любом значении независимой переменной
х, отличном от нуля.
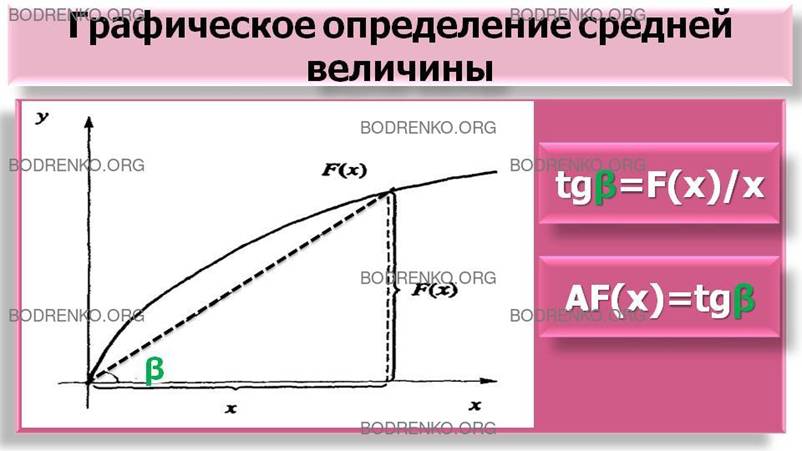
Рисунок 2. Графическое определение средней величины.
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ИЗМЕНЕНИЯ СРЕДНЕЙ ВЕЛИЧИНЫ.
При изменении независимой переменной х угол
β наклона вектора {x,F(x)}также изменяется. Увеличение этого угла с увеличением x свидетельствует о
возрастании средней величины, а
уменьшение - об убывании. В частности,
для приведённого на рисунке 2 графика средняя величина убывает, и её график изображен на рисунке 3.
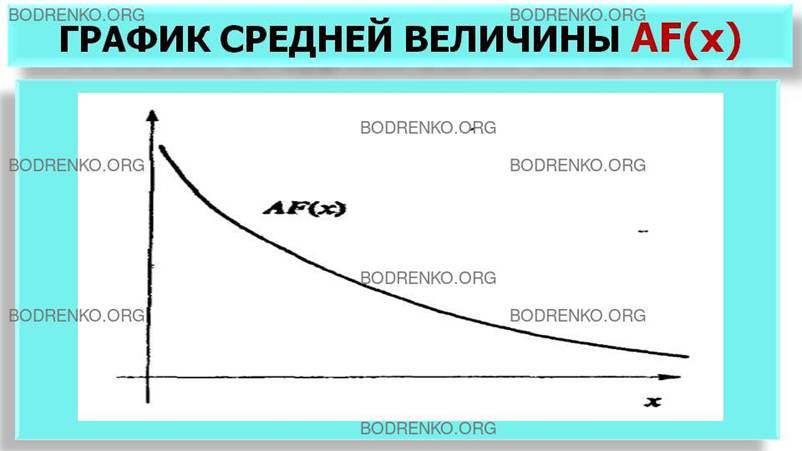
Рисунок 3. График средней
величины AF(x).
НАХОЖДЕНИЕ СУММАРНОЙ ВЕЛИЧИНЫ ПО СРЕДНЕЙ (ОБРАТНАЯ ЗАДАЧА).
Формально обратная задача решается так же, как и прямая, с помощью определения, из
которого находим F(x)=x∙AF(x). Если средняя величина задана в виде графика, представленного
на рисунке 4, то
суммарную величину при данном значении независимой переменной х можно определить как площадь прямоугольника с вершинами в начале координат и точке графика средней величины, имеющей координаты (х, AF(x)), и сторонами x и AF(x).
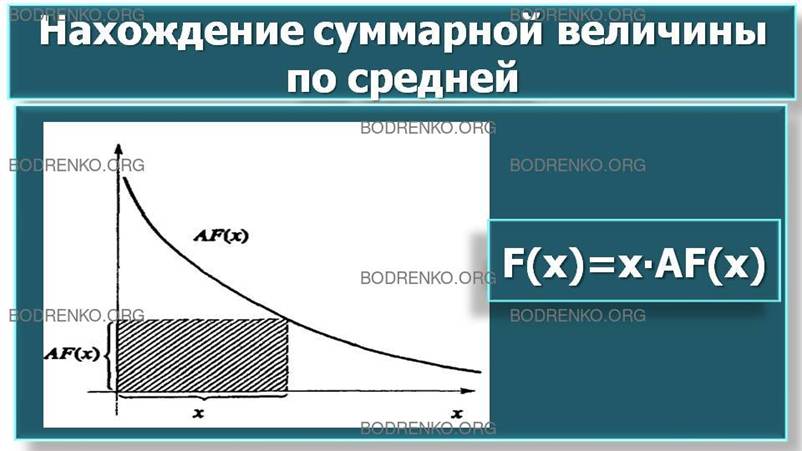
Рисунок 4.
Нахождение суммарной величины по средней.
Определяя характер изменения площади, мы можем построить график суммарной величины. Однако,
на практике, при качественном построении графиков, удобнее применить «метод подбора», т.е. подобрать такую
функцию F(x), чтобы наклон прямой, соединяющей
точки ее графика с
началом координат, изменялся в соответствии с заданным характером изменения средней величины AF(x).
НАХОЖДЕНИЕ МАРЖИНАЛЬНОЙ (ПРЕДЕЛЬНОЙ) ВЕЛИЧИНЫ ПО СУММАРНОЙ (ДЛЯ НЕПРЕРЫВНОГО СЛУЧАЯ).
Формальный и
графический анализ.
Формально эта задача решается с помощью определения
предельной величины МF(x)= F′(x);
ПРИМЕР. Например, если F(x) = x(а- bx∙x), то MF(x) = а – 3bx∙x.

Для графического решения этой задачи (когда суммарная величина
задана в виде графика) необходимо через точку графика суммарной величины,
имеющую координаты
(x,F(x)),
провести касательную к графику. Тангенс угла наклона касательной
к графику суммарной
величины в произвольной точке x, согласно геометрической интерпретации
производной, будет численно
равен производной суммарной величины, а, следовательно, являться предельной величиной MF(x) = F′(x) = tgα(x) (рисунок 5).
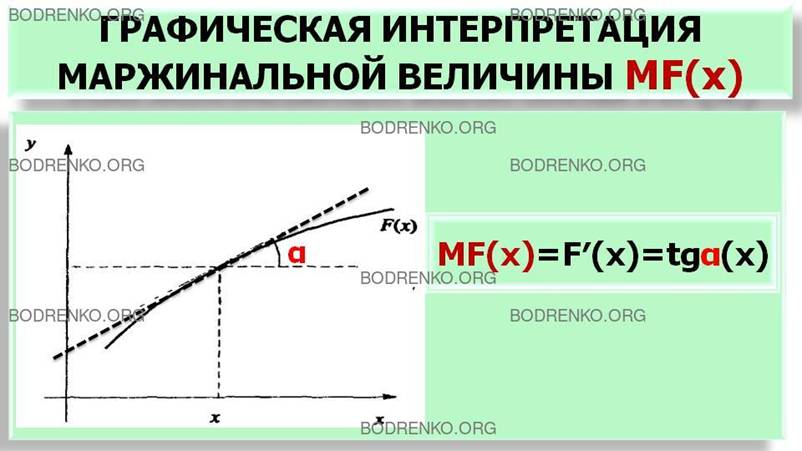
Рисунок 5. Графическая
интерпретация маржинальной величины MF(x).
Геометрическая интерпретация изменения маржинальной (предельной) величины.
При изменении независимой переменной х
угол наклона
касательной α(x) также изменяется. Увеличение этого
угла с увеличением x свидетельствует
о возрастании предельной величины, а
уменьшение - об убывании. В частности, для приведённого на рисунке 5 графика суммарной
величины предельная величина убывает, и её график имеет следующий вид (рисунок 6)
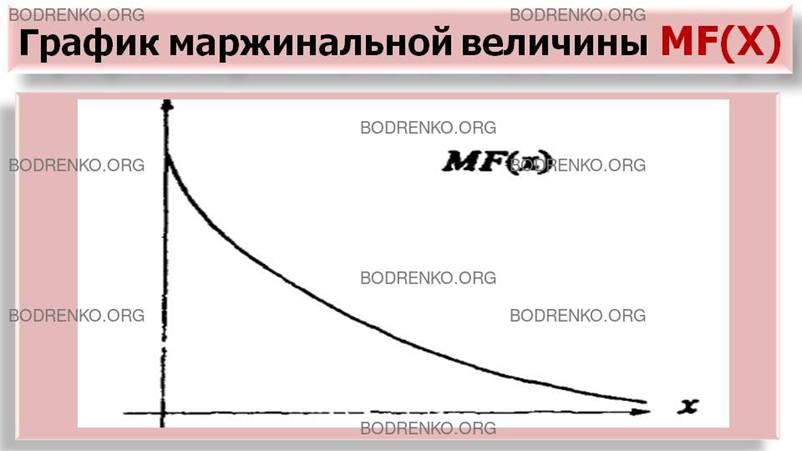
Рисунок 6.
Геометрическая интерпретация изменения маржинальной (предельной) величины MF(x).
НАХОЖДЕНИЕ СУММАРНОЙ ВЕЛИЧИНЫ ПО
МАРЖИНАЛЬНОЙ (ПРЕДЕЛЬНОЙ) (ОБРАТНАЯ ЗАДАЧА).
Формально обратная задача означает
нахождение функции F(x), производная которой F′(x) = MF(x) известна. Для решения
этой задачи служит операция интегрирования, обратная операции дифференцирования. Функция F(x) называется первообразной для функции MF(x) и находится с помощью
неопределенного интеграла F(x) = ∫MF(x)dx.
ПРИМЕР.
Например, если МF(x) = a – bx∙x/3, то
F(x) = ∫MF(x)dx = ∫( a – bx∙x/3)dx = x∙(a – bx∙x) + C, где С – произвольная постоянная.

Здесь мы воспользовались известной
формулой интегрирования степенной функции:
∫xαdx = xα+1/(α+1) + С (α≠-1).
В большинстве практических задач применение операции
интегрирования часто
можно заменить применением так называемого «метода подбора» - т.е. подобрать
такую функцию F(x), что ее производная будет равна данной в
задаче функции MF(x). Этот прием особенно удобно применять для
степенных функций и многочленов, когда операция дифференцирования вызывает понижение показателя степени на
единицу, а операция интегрирования - повышение показателя степени на единицу.
Если предельная величина задана в виде графика, то, согласно геометрической интерпретации
неопределенного интеграла, площадь подграфика функции предельной величины в диапазоне изменения независимой переменной от нуля до х будет равна
суммарной величине минус некоторая постоянная С: или F(x) = S(x) + С.

Рисунок 7. Геометрическая
интерпретация суммарной величины F(x).
Если при x→0 площадь S(x) →0, то константу C можно найти как значение суммарной величины при x = 0. Например, при нахождении суммарного дохода R(Q) = p∙Q чаше всего R(0)=0, и С=0; при нахождении
суммарных издержек С(Q) постоянная С= С(0) имеет
смысл фиксированных (постоянных) издержек.
СООТНОШЕНИЯ МЕЖДУ СРЕДНИМИ (AF) И МАРЖИНАЛЬНЫМИ (ПРЕДЕЛЬНЫМИ) (MF) ВЕЛИЧИНАМИ.
Задача нахождения по одной из этих
величин другой может быть сведена к одной из предыдущих задач, если, предварительно,
мы найдём суммарную величину. Например, если
дана средняя величина AF(x), то суммарная величина F(x) = х∙АF(x), а предельная MF(x) = F′(x) = (х∙АF(x))′= AF(x) + х∙АF′(х).
Аналогично, можно выразить среднюю
величину через суммарную:
AF(x) =(1/x)∙∫MF(x)dx.

Первое из этих соотношений, а именно
соотношение:
MF(x)= AF(x) + х∙АF′(х), имеет простую интерпретацию.
В точке экстремума функции AF(x) ее производная AF'(x) =0, и, следовательно, предельная величина
совпадает со средней в точке экстремума
последней. Предположим, что независимая переменная может принимать
только положительные значения (х > 0), тогда:
а) в области возрастания функции AF(x) её производная AF′(x) > 0, и MF(x) > AF(x) (предельная величина больше
средней);
б) в области убывания функции АF(х) её производная AF′(x< 0, и MF(x) < AF(x) (предельная величина меньше средней).
Таким образом, график предельной величины лежит выше графика средней величины в
области возрастания последнего, ниже - в области убывания, и проходит
через точку экстремума графика средней величины.
Примеры соотношения между графиками
средних и предельных издержек (АС и МС), а также между графиками среднего и предельного
продуктов труда (APL и MPL) , приведены на рисунках 7, 8.
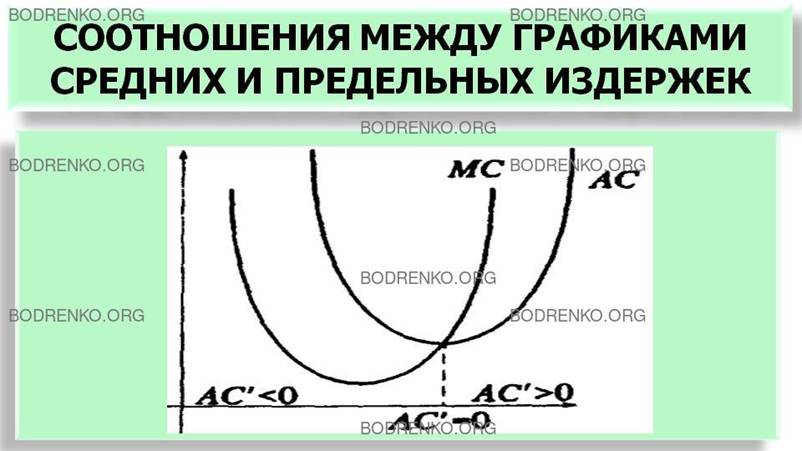
Рисунок 7.
Соотношение между графиками средних и предельных издержек AC и MC.
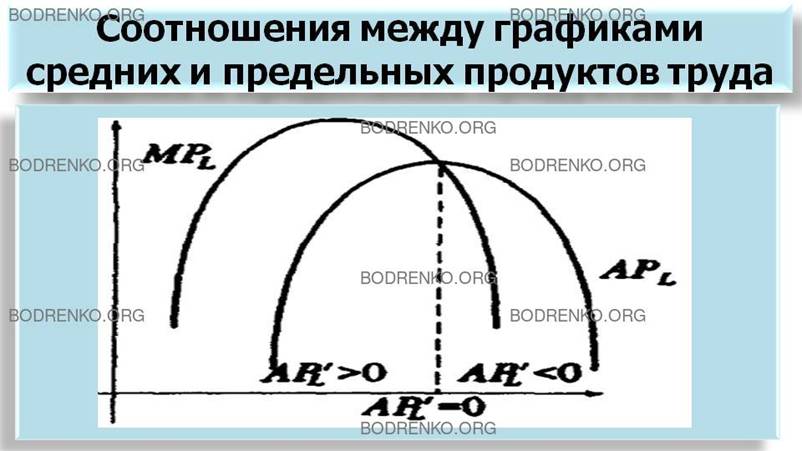
Рисунок 8.
Соотношение между графиками среднего и предельного продуктами труда APL и MPL.
ДИСКРЕТНЫЙ СЛУЧАЙ.
Если независимая переменная х может принимать только дискретные значения (например, объём
выпуска автомобилей
фирмой, количество нанимаемых ею рабочих и т.д.). то все полученные выше соотношения
сохраняют свой вид при следующих
условиях:
а) производная F′(x) заменяется на отношение:ΔF/Δx;
б) интеграл ∫MF(x)dx заменяется на конечную сумму ∑{x}MF(x);
в) касательная к графику функции F(x) заменяется на прямую
линию, проходящую через две точки с координатами (х,F(x)) и ((x+Δx); F(x+Δx)).
Соотношение между средними и
предельными величинами в дискретном
случае имеет простую интерпретацию. Представим себе ученика-«хорошиста», который получает одни четвёрки.
Каждую последующую
оценку можно интерпретировать как предельную оценку, а средний балл - как среднюю оценку. Если этот
ученик решит стать «отличником» и будет получать в дальнейшем одни пятёрки (предельная
оценка выше средней), то его средняя оценка будет постепенно повышаться. Если ученик,
наоборот, разленится и превратится в
«троечника», начав получать одни тройки
(предельная оценка станет меньше средней), то его средняя оценка будет понижаться.
РАЗДЕЛ 3. ФУНКЦИИ СУММАРНОГО, СРЕДНЕГО И ПРЕДЕЛЬНОГО ДОХОДА И
ИЗДЕРЖЕК.
В качестве примера применения
соотношений между предельными,
средними и суммарными величинами рассмотрим экономические показатели, характеризующие работу фирмы: Q -
объем выпуска, р -
цена, R = p(Q)∙Q- доход (выручка). С- издержки, Π=R – C - прибыль - для двух типов рыночной
структуры: совершенной конкуренции и монополии.
СОВЕРШЕННАЯ КОНКУРЕНЦИЯ.
В этом случае цена на продукцию фирмы
не зависит от объёма производства данной фирмы, а определяется рынком и постоянна. Цена p(Q)=p=const. Следовательно, R(q)
= pQ. Доход является линейной функцией объёма выпуска. Для типичной функции издержек (растущих быстрее чем доход
при малых объёмах выпуска) графики дохода, издержек и прибыли показаны на рисунке 9.
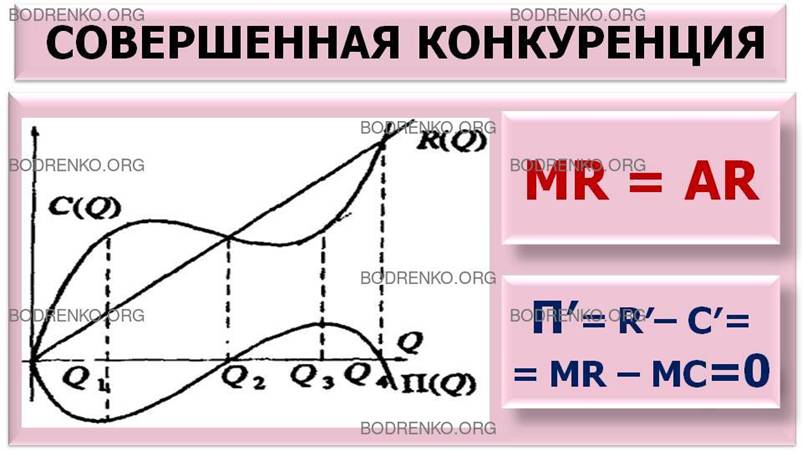
Рисунок 9. Графики
дохода, издержек и прибыли (совершенная конкуренция).
По ним можно построить графики средних и предельных величин. Так как MR = (pQ)' =p = (pQ)/Q = R(Q)/Q = AR, то графики среднего и предельного
дохода имеют вид прямой, параллельной оси Q.

График средних издержек пересекается с графиком
среднего дохода при объёмах выпуска Q2
и Q4, (так как в этих точках значения функций C(Q) и R(Q) совпадают), лежит выше него при Q< Q2 и Q > Q4, (из C(Q) > R(Q) следует, что AC(Q) =С(Q)/Q >R(Q)/Q =
AR(Q)) и ниже - при Q2< Q < Q4. В точке, лежащей чуть ниже Q3 (для данных графиков на рисунке 9) средние издержки минимальны.
Эту точку можно найти, проводя из начала координат прямую, касающуюся
графика C(Q).
График предельных издержек можно построить,
анализируя изменение наклона касательной к графику C(Q). В точках Q1 и Q3 касательная к графику C(Q) параллельна графику дохода R(Q). Следовательно, в этих точках
предельные издержки совпадают с предельным доходом и имеет место
минимум прибыли (максимум убытков) в точке Q1, и максимум прибыли в точке
Q3 (Π′ = R′ - С′= MR- МС=0, ибо, как
видно из рисунка 9, прибыль положительна при объёме выпуска Q2< Q< Q4, отрицательна при Q<Q2 и Q> Q4. Величину прибыли при оптимальном объёме
выпуска (Q3) можно найти как площадь заштрихованного прямоугольника по графикам средних издержек и среднего дохода (рисунок 10). (Вершины
прямоугольника находятся в точках с координатами: (Q3, p), (Q3,AC(Q3)), (0,AC(Q3)), (0, p)).
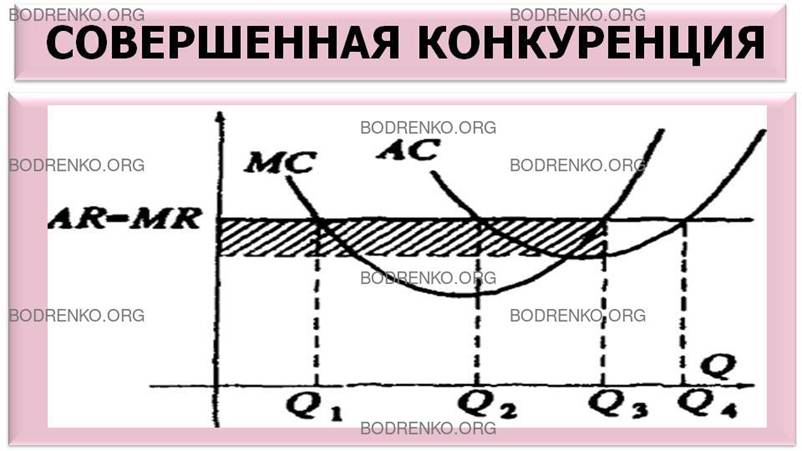
Рисунок 10.
Величина прибыли при оптимальном выпуске (совершенная конкуренция).
МОНОПОЛИЯ.
В случае монополии фирма сама выбирает цену, исходя из кривой спроса p(Q) на её продукцию. Поскольку p(Q) - убывающая функция, p′(Q)<0.
При той же функции издержек, что и в предыдущем случае, графики суммарных, средних и предельных показателей показаны на рисунках 11, 12. При этом графики суммарных, средних и предельных
издержек имеют тот же вид, что и предыдущем случае.
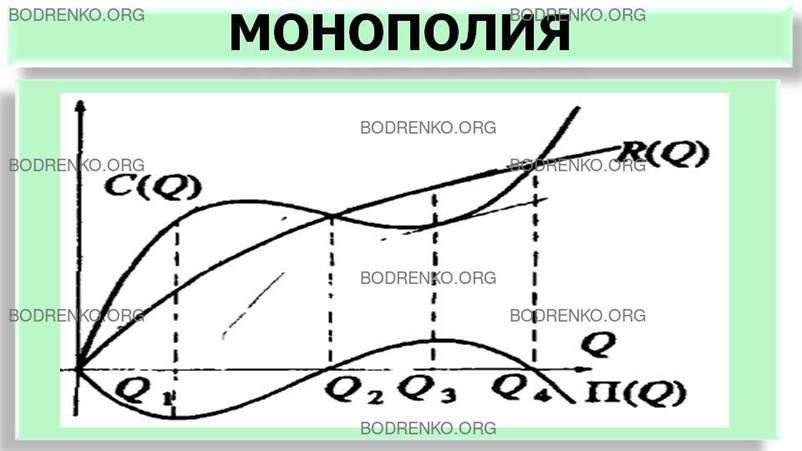
Рисунок 11. Графики дохода, издержек и прибыли (монополия).
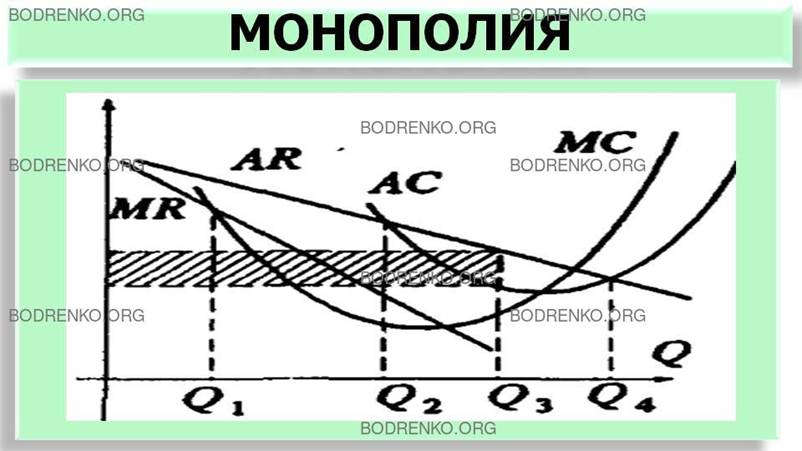
Рисунок 12. Величина прибыли
при оптимальном выпуске (монополия).
График среднего дохода AR =(p(Q)∙Q/Q)=p(Q) совпадает с графиком функции
спроса и пересекает график средних издержек в точках Q2 и Q4 (где R(Q) = C(Q)). График предельного дохода лежит ниже
графика среднего
дохода при любых объёмах выпуска, так как MR = R′(Q) = (p(Q)∙Q)' = p(Q) + Q∙p′(Q) =AR+ Q∙p′(Q) < AR, (поскольку p′(Q) < 0), и пересекает график предельных издержек в точках
Q1 и Q3, в которых касательные к графикам дохода и издержек параллельны.

При этих объёмах выпуска прибыль, как и в предыдущем случае, принимает минимальное и максимальное значения соответственно. Это обусловлено тем,
что необходимое
условие максимума прибыли по-прежнему записывается как Π′ = R′ -
С′= MR- МС=0, и в оптимальной точке предельный доход обязательно равен предельным издержкам.
Аналогично предыдущему случаю, прибыль на графиках средних и
предельных величин также можно определить как площадь заштрихованного прямоугольника,
построенного между графиками среднего дохода и средних издержек (вершины прямоугольника находятся в
точках: (Q3, AR(Q3)), (Q3,AC(Q3)), (0,AC(Q3)), (0, AR(Q3))).
Итак, при определении оптимального
объема производства фирмы, если
известны ее функции суммарного дохода и издержек R(Q) и C(Q) (предполагается, что эти функции
дифференцируемы), средние и предельные показатели могут быть использованы следующим образом.
Вначале находятся точки, в которых
величина предельного дохода равна
величине предельных издержек: MR(Q)=MC(Q). Если таких точек нет, то фирме либо невыгодно производить вообще
(при R(Q)< С(Q)), либо выгодно сколь угодно
наращивать объем производства
(при R(Q)>C(Q)).
В найденных точках может достигаться
максимум прибыли, максимум
убытка, минимум прибыли, минимум убытка, либо ничего из перечисленного. Поэтому далее среди
этих точек находятся те, в которых функция прибыли Π(Q)= R(Q) – C(Q) достигает максимума (ее производная меняет знак с плюса на
минус). Это точки максимума
прибыли или минимума убытка. Наконец, нужно выбрать точки (точку), где величина прибыли
положительна. Признаком этого может быть превышение среднего дохода над средними издержками: AR(Q)>MR(Q). Если такая точка найдена, то она
является
точкой (локального) максимума прибыли фирмы.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Замков О.О., Толстопятенко А.В.,
Черемных Ю.М. Математические методы в экономике: Учебник. 2-е изд. - М.: МГУ
им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. — 368 с.
[2] Фомин Г. П. Математические
методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и
доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

[3] Шелобаев
С. И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. —
М.: ЮНИТИ - ДАНА, 2001. - 367 с.
[4] Шикин Е.
В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб.
пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический
университетский учебник»).
[5]
Экономико-математические методы и прикладные модели: Учебное пособие для вузов/
В.В. Федосеев, А.Н. Гармаш, Д.М.
Дайитбегов и др.; Под ред. В.В. Федосеева. — М.: ЮНИТИ, 1999. - 391 с.
