Математическое моделирование экономических систем. Динамические модели в управлении экономическими системами. Экономика как динамическая система. Теория равновесия в экономическом анализе. Динамические теории в экономике. Динамические модели: модель народонаселения, модель мобилизации, модель гонки вооружений
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Математическое моделирование экономических систем
Лекция 6
Тема лекции 6. «Динамические модели в управлении
экономическими
системами»

Разделы лекции:
1. Экономика как динамическая система.
2. Теория равновесия в экономическом
анализе. Динамические теории в экономике.
3. Примеры динамических моделей: модель
народонаселения, модель мобилизации, модель гонки вооружений.

РАЗДЕЛ 1. ЭКОНОМИКА КАК ДИНАМИЧЕСКАЯ
СИСТЕМА.
В ЧЕМ ПРОЯВЛЯЕТСЯ МАТЕМАТИЗАЦИЯ
ЭКОНОМИЧЕСКОЙ НАУКИ НА СОВРЕМЕННОМ ЭТАПЕ ЕЕ РАЗВИТИЯ?
Характерной чертой современного этапа
развития экономической науки является ее математизация, которая проявляется в
замене изучаемого экономического процесса адекватной математической моделью и
последующем исследовании свойств этой модели либо аналитическими методами, либо
на основе проведения вычислительных экспериментов.
КАКИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ПЕРВОНАЧАЛЬНО ИСПОЛЬЗОВАЛИСЬ В ЭКОНОМИКЕ?
Использование математических моделей в
экономике имеет более чем столетнюю историю. Например, одна из первых моделей
рыночной конкуренции (О. Курно) была опубликована в 1838 году, а через полвека
Л. Вальрас уже применял математические модели при чтении курса политической
экономии в Лозаннском университете. К настоящему времени в экономической теории
прочно закрепились различные модели взаимодействия рынков рабочей силы, товаров
и денег, модели однопродуктовой и многопродуктовой фирм, модель поведения
потребителя, модель конкуренции фирм на рынке товаров и другие, которые, по
существу, являются равновесными моделями.

ПОЧЕМУ ВАЖНЫ ИССЛЕДОВАНИЯ РЕАЛЬНЫХ
ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ В ДИНАМИКЕ?
Подавляющее большинство экономических
процессов протекает во времени, вследствие чего соответствующие математические
модели являются в принципе динамическими. Одним из традиционных подходов к
прогнозированию развития экономических процессов служит изучение смещения точки
равновесия динамической системы, вызванного изменением тех или иных параметров
модели. Такой (квазистационарный) подход опирается на ключевую концепцию
классической политэкономии — «невидимую руку» Адама Смита. Как известно, эта
концепция опирается на гипотезу о существовании на конкурентных рынках
автоматического равновесного механизма.
ЧЕМ БЫЛО ОПРАВДАНО ИСПОЛЬЗОВАНИЕ КВАЗИСТАЦИОНАРНОГО ПОДХОДА К
АНАЛИЗУ ДИНАМИЧЕСКИХ ПРОЦЕССОВ ЭКОНОМИКИ?
Использование квазистационарного
подхода к анализу динамических процессов экономики привело к распространению
общего представления о том, что развитие любой сложной системы можно
рассматривать как смену одного устойчивого состояния другим с кратким периодом
переходного процесса между ними. Однако анализ реальной экономической динамики
на основе такого подхода может оказаться ошибочным, поскольку период
неравновесного развития многих экономических процессов может оказаться слишком длительным,
чтобы им можно было пренебречь. Прекрасно понимая важность исследования
экономических процессов в динамике, классик современной экономической науки А.
Маршалл оправдывал использование квазистационарного подхода для оценки
изменений на рынке тем, что «наш анализ все еще пребывает в младенческом
возрасте».
ПОЧЕМУ ИССЛЕДОВАНИЯ ДИНАМИКИ
ЭКОНОМИЧЕСКИХ СИСТЕМ СТАНОВЯТСЯ АКТУАЛЬНЫМИ?
Отметим, что квазистационарный подход является эффективным лишь до поры до
времени, пока, в силу некоторых причин, характер стационарного состояния не
изменится кардинальным образом. Подобные изменения, называемые бифуркациями,
принадлежат уже к области приложений методов нелинейного динамического анализа,
развитие которого приводит ко все большему распространению такой точки зрения:
«Мир — это постоянное развитие, вечная неустойчивость, а периоды стабилизации —
лишь краткие остановки на этом пути». Неудивительно, что эта универсальная
методология, возникшая сравнительно недавно и хорошо зарекомендовавшая себя в
естествознании, стала проникать и в традиционно гуманитарные науки, в первую очередь в экономику. Не боясь
ошибиться, можно утверждать, что любой раздел экономической науки может быть
отнесен к области приложений синергетики, поскольку при рассмотрении любого
динамического экономического процесса всегда присутствует в качестве
действующего фактора некоторый активный, то есть осуществляющий обратную связь
элемент. Поэтому, если мы хотим заглянуть за горизонт узкого мира, в котором
все представляется устойчивым, и в котором нет места катастрофам и
перестройкам, нам не обойтись без использования синергетического подхода. Время
изменяет не только экономический уклад общества, но вносит свои поправки в
ключевые экономические идеи. Сегодня слишком рано судить об историческом
значении вклада в экономическую науку новейших экономистов, поскольку
экономисты-классики, такие как Рикардо, Мальтус, Маркс, Вальрас и Маршалл жили
в иное время, и принадлежат иным
культурам. Время — лучший арбитр. Только время придает нам достаточно мудрости,
чтобы признать, что иные идеи, которые казались сначала такими значительными и
многообещающими, имеют довольно поверхностный характер. Не только широкая
публика, но многие экономисты все больше утрачивают веру в возможность
применения экономической науки к реальности, хотя уровень экономических знаний
в последнее время значительно вырос: видимо, между научным знанием и доверием к
науке нет простой зависимости. Можно придумать множество причин, по которым
экономика ошибается в своих попытках объяснить действительность. С одной
стороны, сам реальный мир резко усложнился в последние десятилетия. Технология,
институты общества, качество жизни,
устремления людей, их нравы, которые в прошлом менялись относительно медленно,
сейчас, как правило, изменяются гораздо быстрее. Эта особенность современного
общества делает затруднительными, если не просто невозможными, попытки
объяснения экономической жизни с позиций чистой науки. С другой стороны,
традиционная теоретическая экономика имеет свои внутренние ограничения: она
ограничена преимущественно статическими и стабилизированными извне
экономическими системами. Нелинейные неустойчивые процессы, такие, как
регулярные и нерегулярные колебания, в традиционном анализе считаются
случайными, либо незначительными явлениями.
КАКИЕ ЭТАПЫ В РАЗВИТИИ ТЕОРЕТИЧЕСКОЙ ЭКОНОМИКИ МОЖНО ВЫДЕЛИТЬ?
Поль А. Самуэльсон, когда писал свои
выдающиеся «Основы экономического анализа», разделял развитие аналитической
экономики примерно на пять больших этапов.
1. Первый этап связан с именем
Вальраса, у которого мы находим кульминацию идеи детерминированного равновесия
и статического уровня.
2. Парето и другие сделали следующий
шаг, который лег в основу теории сравнительной статики.
3. Третий шаг, связанный с
максимизацией действия экономического объекта, был сделан Джонсоном, Слуцким,
Хиксом и Алленом.
4. Четвертое достижение связано с
открытием принципа соответствия.
5. «Пятый шаг, который естественно
сделать после того, как мы исследовали отклик системы на изменение заданных параметров
— это исследовать ее поведение в зависимости от времени». Более того, Самуэльсон подчеркивал, что
«польза от любого теоретического построения состоит в том, чтобы понять
характер поведения экономических переменных в зависимости от определенных данных
или параметров. Это справедливо как для динамики, так и для статики.
Следовательно, следующим логическим шагом должно быть именно создание теории
сравнительной динамики. Она должна не только включить в себя теорию
сравнительной статики как частный случай, а также все перечисленные выше
разделы экономической теории, но покрывать значительно более широкую область» (Самуэльсон,
1946).
На этой лекции мы коснемся проблем,
связанных с динамикой экономических систем.
ПОЧЕМУ ВАЖНЫ МЕТОДЫ НЕЛИНЕЙНОГО ДИНАМИЧЕСКОГО
АНАЛИЗА В ИССЛЕДОВАНИИ ЭКОНОМИЧЕСКИХ СИСТЕМ?
Любая теория может объяснить лишь
некоторые аспекты реального мира. Экономическая теория, которая стремится
объяснить долговременную экономическую эволюцию, может оказаться бессильной
объяснить кратковременные экономические явления, подобно тому, как теория быстрых процессов Кейнса может быть
непригодна для долгоживущих социальных систем Шумпетера. Однако, если экономисты отдадут себе отчет,
какие предположения явно или неявно приняты в экономической теории, и, до того
как начинать дебаты, определятся в том, к какому классу отнести экономическое
явление, которое подлежит теоретическому осмыслению, то взаимные недопонимания
между различными школами могут быть в значительной степени устранены. Важно понимать, при каких примерно условиях
применимы результаты каждой из экономических теорий.
Столкнувшись с ошибками традиционной
экономики при объяснении реальных явлений, экономисты попытались ввести в
экономику такие понятия, как несовершенная конкуренция, неполная информация и
нерациональность. К настоящему времени на этом пути предложено немало теорий.
Мы имеем неравновесную макроэкономику, экономику семьи, частную экономику, и
так далее. Очень популярно также использовать микроэкономический подход к анализу
макроэкономических процессов. В наше время и реальная экономика, и
экономическая теория стали «хаотическими». Упростить экономические явления мы
не можем. Но в основе человеческой природы лежит стремление к истине с позиций
простоты и красоты. Для объяснения сложности реального мира мы всегда пытаемся
отыскать простые и универсальные пути. И для нас естественно пытаться построить
теорию, которая могла бы объяснять сложные явления, используя, насколько это
возможно, простые концепции и методы. И раньше, в 1930-х и 1940-х годах,
находились экономисты, сознававшие значение неустойчивости нелинейных
динамических систем для экономики. В основном это были экономисты, которые
изучали деловые циклы. Однако нельзя сказать, чтобы они систематически
использовали понятие неустойчивости или рассматривали его как источник
сложности реального мира. Фактически для экономистов было почти невозможно без
затруднений принять идеи нелинейности, поскольку хаотические явления в
неустойчивых нелинейных динамических системах могут быть поняты только с
помощью математики и находятся за пределами наших интуитивных представлений. Но
даже математики мало знали о нелинейных неустойчивых динамических системах в то
время.
После второй мировой войны произошло
удивительное экономическое явление: две страны — Западная Германия и Япония,
которые подверглись значительным разрушениям в ходе войны (по крайней мере, физическим),
были восстановлены и стали развиваться с большой скоростью. Бурный
экономический рост, быстрая урбанизация и многочисленные экономические успехи
наблюдались в послевоенные годы и в других странах, хотя иногда их развитие
характеризовалось значительными (нерегулярными) флуктуациями. Даже внутри одной
страны в различных регионах имелись различия. Порой они бывали столь велики,
что можно было подумать, будто люди, населяющие разные области, проживают не в
одной и той же стране. Отсюда можно сделать очевидный вывод: время и место
играют определяющую роль в формировании и изменении характеристик индивидуумов
и сообществ.
Экономисты предложили много теорий для
объяснения феномена экономической эволюции. Однако теория экономической
динамики все еще использует упрощенные подходы. До сих пор основной интерес в
литературе был сосредоточен на условиях существования, единственности и устойчивости
стационарных состояний. К несчастью, в реальной экономике эти типы поведения не
зарегистрированы.
Вместо этого реальная экономика
проявляет сложную динамику: периодические циклы, нерегулярные флуктуации и
хаос. Между действительным экономическим развитием и экономическими теориями
имеет место разрыв, и этот разрыв не сокращается с течением времени. Когда бы
экономисты ни обращались к проблемам динамики, они находят повод для
разногласий. Безусловно, с одной стороны, это может происходить вследствие
сложности экономических систем, с другой стороны — из-за отсутствия
взаимопонимания между самими экономистами. Более того, любопытно, что разрыв
между теорией и действительностью не сокращается с появлением мощных
компьютеров и накоплением статистических данных. Видимо, вера в то, что
усовершенствования в технике вычислений и моделировании могут решить все
проблемы экономического развития, вряд ли оправдана — анализ реальных данных
мало о чем говорит, если он надежно не подкреплен хорошей теорией.
РАЗДЕЛ 2. ТЕОРИИ РАВНОВЕСИЯ В
ЭКОНОМИЧЕСКОМ АНАЛИЗЕ. ДИНАМИЧЕСКИЕ
ТЕОРИИ В ЭКОНОМИКЕ.
ТЕОРИИ РАВНОВЕСИЯ В ЭКОНОМИЧЕСКОМ
АНАЛИЗЕ.
Перед тем как дать обзор основных
концепций теории экономической динамики, мы поясним, как важна для понимания
динамической экономики экономика статическая.
Неопровержимым аргументом здесь служит
то обстоятельство, что наиболее важные результаты в экономическом анализе были
получены из равновесных теорий. Подобно некоторым другим концепциям
экономического анализа, понятие «равновесия» в экономике позаимствовано из
теоретической механики. Концепция равновесия была известна механикам задолго до
публикации «Благосостояния наций» в 1776 году, и совершенно очевидно, что Адам
Смит черпал свои идеи в некоторых механических аналогиях. Однако поскольку в
действительности не существует такой экономики, которая могла бы быть
зафиксирована в состоянии покоя, анализ равновесий имеет явно ограниченную
применимость. Возникает вопрос, возможно ли, пользуясь методами равновесного
анализа, пролить какой-то свет на проблемы эволюции. Тем не менее, развитие
экономической теории
доказало, что анализ равновесий
является весьма и весьма полезным.
Интерес экономистов к равновесным
ситуациям можно оправдать двояко. Во-первых, состояния равновесия имеют особые
права на наше внимание, потому что когда мы спрашиваем себя, как устроена такая
децентрализованная экономика, которая еще и эффективна мы обнаруживаем, что
зачастую такая экономика находится в конкурентом равновесии (которое
представляет собой стационарное состояние). Конечно, это не должно означать,
что всякая система совершенной конкуренции обязана иметь выраженную тенденцию к
равновесию — простейшим примером тому является паутинообразная динамика
конкурентной модели («теорема о паутине»). Более того, в современной литературе
о деловых циклах и экономическом хаосе показано, что стремление к равновесию
имеет место лишь в ограниченном ряде случаев. Вторым аргументом в пользу
изучения равновесий, который был выдвинут первоначально Маршаллом, является утверждение
о том, что в любой реальной экономике, если она не находится в состоянии
равновесия, действуют силы которые стремятся вернуть ее к равновесию. Те же
основополагающие аргументы можно обнаружить и в обосновании концепции
«невидимой руки» Смита. Последний термин означает что социальная система,
движимая под действием независимых сил к различным состояниям, согласуется при
этом с окончательным Положением равновесия. В итоге результаты конкуренции
могут быть совершенно отличны от тех, которые имелись в виду участниками. Смит
сформулировал наиболее важный вывод общей равновесной теории — способность
конкурирующей системы достигать такого распределения ресурсов, которое в
определенном смысле оказывается эффективным. Рикардо (1817), Милль (1848) и
Маркс (1867), чьи работы заполнили некоторые логические пробелы у Смита, все
могут быть отнесены к ранним представителям общей теории динамического
равновесия. Однако никто из классиков не владел верной общей теорией
равновесия, никто явно не сформулировал роль спроса.
Шумпетер (1934, 1975) имел близкую
Маршаллу точку зрения относительно равновесий. Однако, согласно Шумпетеру, в
капиталистической системе экономическое равновесие вообще не может быть
достигнуто, потому что всегда существуют новшества, которые сдвигают систему из
положения равновесия — тем не менее, он считал важным изучение равновесных
структур, так как они позволяют прояснить тенденцию реальных процессов
экономической эволюции.
Полная формулировка общей концепции
равновесия может быть отнесена на счет Вальраса, хотя многие ее элементы были
независимо разработаны В. С. Джевонсом и С. Менгером. Работы Вальраса заложили
фундамент, на который и поныне опираются экономисты. Чтобы охватить области
обмена, производства, капитала и денег, он развил общую теорию равновесия в
унифицированной формулировке.
Модели равновесия Вальраса вновь стали
обсуждаться в начале 1950-х годов (см., например, Дебрэ, 1959, Эрроу и Хан,
1971). Работы последних, которые часто называют общей теорией равновесия, были
сфокусированы на вопросе существования конкурентных равновесий, гарантированных
равновесными ценами.
Таким образом, общий динамический
анализ предопределен устойчивостью таких равновесий. Динамика здесь, в
основном, состоит в «искусственных» процессах регулирования цен. Она
существенным образом связана с устойчивостью равновесия, определенного в рамках
статики (Эрроу и Хан, 1971).
В известной книге «Основы
экономического анализа» Самуэльсон (1947) отстаивает использование концепции
равновесия, аргументируя это тем, что многие экономические проблемы могут
рассматриваться как задачи максимизации и минимизации. По Самуэльсону, теория
поведения потребителя и фирмы являются простыми приложениями методов условной
максимизации (максимизации с ограничениями). Этот аппарат обнаруживает не
только единую структуру, лежащую в основе самых разных проблем, но и служит
источником новых теоретических предсказаний. Одним из наиболее популярных
методов, используемых при этом подходе, является сравнительный статический
анализ, суть которого заключается в изучении влияния сдвига значений
экономических параметров. Метод дает нам информацию о том, как изменится
равновесие в результате экзогенных воздействий (шоков). Он нашел широкое
применение в различных задачах экономики.
ДИНАМИЧЕСКИЕ ТЕОРИИ В ЭКОНОМИКЕ.
Время должно входить в качестве
независимой переменной в описание каждой экономической величины. Никакая теория
экономической динамики не может избежать рассмотрения временных зависимостей. В
теориях равновесия время исключено, потому что предполагается, что систему
можно поддерживать в таком состоянии, когда отношения взаимодействия между
переменными остаются неизменными. Это предположение справедливо, если период
наблюдения очень короток или если мы имеем дело только со стационарными состояниями,
и следовательно, время не играет роли. До известной степени, равновесный анализ
можно рассматривать как частный случай анализа динамического. По теории
экономической динамики имеется обширная литература. Основные работы в области
экономической эволюции относятся к вопросам экономического роста и деловых
циклов. Экономический рост является классическим предметом экономики.
Значительный вклад в его теорию сделан Адамом Смитом, Д. Рикардо, Т. Р.
Мальтусом, К. Марксом, Дж. Миллем и другими. В течение периода с 1870 по 1920
годы в литературе доминировали подход частичного равновесия Маршалла и подход
общего равновесия Вальраса. В трудах Бома-Баверка, Кларка, Викселла и Фишера
большое развитие получили также теории капитала и прибыли. Однако, по крайней мере,
в свете современных представлений, их работы часто страдали упрощением
формулировок и неверными выводами. Можно считать, что «Социализм, капитализм и
демократия» (1975), «Теория экономического развития» (1934) Дж. А. Шумпетера и
«Теория экономического роста» В. А. Льюиса (1955) также не выходят за рамки
классических традиций. Все эти работы характеризуются тем, что для объяснения
хода экономического развития принимают во внимание не только «чисто
экономические переменные», но также и некоторые социальные факторы, такие как
мораль, этика, общественные институты и т. д.

В эволюционной системе Шумпетера важную
роль при построении теории играет концепция инновации. Это понятие относится к
различным аспектам нововведений — таким, как появление новых потребностей и
изменение ориентации, составляющие часть процесса социального обучения;
разработка новых товаров, удовлетворяющих нужды потребителей; использование
новых товаров и оборудования для усиления конкурентоспособности; предложение
новых организационных методов и открытие новых рынков. В силу существования
инноваций, конкурентная капиталистическая экономика не может быть устойчивой .
Однако, по Шумпетеру, такая неустойчивая эволюция не означает разрушения
системы. Каждому экзогенному воздействию соответствует новое состояние
равновесие, в направлении которого движется реальная система. К настоящему
времени для объяснения динамики экономических систем ряд ученых, воодушевленных
перспективами, открытыми Шумпетером, разработали «эволюционную экономику» (см.,
например, Нельсон и Винтер, 1982). Здесь термин «эволюция» зачастую относится к
долговременным процессам и прогрессивным переменам.
Термин «вне-равновесие» при их подходе
является ключевым словом в большей степени, нежели термин «равновесие». В этом
отношении синергетическая экономика оказывается весьма похожей на «эволюционную
экономику». Интерес к макроэкономической теории роста возродила «Общая теория»
Кейнса. «Общая теория» обрисовала картину взаимодействий агрегированных
макроэкономических переменных.
Следует заметить, что для Кейнса и
некоторых его последователей эволюция капиталистической системы является
потенциально нестабильной, тогда как, согласно неоклассическому подходу,
экономический рост характеризуется как устойчивый процесс. Кейнс полагал, что
правительство может стабилизировать экономику, принимая верные политические
решения. Таким образом, одной из основных проблем кейнсианской теории является
вопрос о том, каким образом стабилизировать экономическую систему. Значительную
роль в развитии современной экономической теории роста сыграли работы
Самуэльсона, Солоу, Моришимы, Хикса, Леонтьева и других. Эти работы
сфокусированы на процессах аккумуляции капитала, переплетающихся с увеличением
производства и потребления, но почти все они выполнены в предположении
заведомой устойчивости систем. О том, что будет, если система находится в
неустойчивом состоянии, сказано мало.
Между классической и современной
теориями экономического роста существует множество различий. Например,
эмпирические факты, которые пытается объяснить современная экономика роста,
совершенно отличны от тех, с которыми имеет дело классическая. Так, оказалось,
что некоторые из наиболее важных предсказаний теории Мальтуса и Рикардо, не
реализуются. Вопреки им, сегодня доля землевладельцев не выглядит возрастающей,
население не растет быстрее, чем продукты, а роль сельского хозяйства по
отношению к промышленности заметно снижается.
С другой стороны, основным предметом
современной экономики роста является объяснение сдвигов в производстве,
занятости и акционерном капитале растущей экономики и взаимоотношения между
этими переменными, а также объяснение движения распределения дохода между
участниками производства. Современная теория роста пытается очертить
концептуальные рамки, в которых могут иметь место гораздо более значительные
эмпирические исследования. Типы экономик, которые пытается описать современная
теория, являются существенно боле развитыми и индустриализированными. Капитал и
труд в таких экономиках — две отправные точки, на которых фокусируется основное
внимание. Земля, которая является важным фактором в классической теории роста,
здесь обычно игнорируется. Анализ в основном концентрируется на соотношениях
«потребление-инвестиции», а не на распределении между альтернативными
инвестициями или альтернативными потребительскими товарами.
РАЗДЕЛ 3. ПРИМЕРЫ ДИНАМИЧЕСКИХ
МОДЕЛЕЙ: МОДЕЛЬ НАРОДОНАСЕЛЕНИЯ, МОДЕЛЬ
МОБИЛИЗАЦИИ, МОДЕЛЬ ГОНКИ ВООРУЖЕНИЙ.
Не ставя перед собой задачи дать сколько-нибудь
полную классификацию существующих моделей, сначала коротко опишем некоторые их
типы.
1. ФИЗИЧЕСКИЕ МОДЕЛИ.
Так называют увеличенное или уменьшенное описание
объекта или системы. Отличительная характеристика физической модели состоит в
том, что в некотором смысле она выглядит как моделируемая целостность. Наиболее
известным примером физической модели является копия конструируемого самолета,
выполненная с полным соблюдением пропорций, скажем 1:50. На одном из этапов
разработки самолета новой конструкции возникает необходимость проверить его основные
аэродинамические параметры. С этой целью подготовленную копию продувают в
специальной (аэродинамической) трубе, а полученные показания затем тщательно
исследуют. Выгодность такого подхода совершенно очевидна. И потому все ведущие
самолетостроительные компании используют физические модели подобного рода при
разработке каждого нового летательного аппарата. Часто в аэродинамическую трубу
помещают уменьшенные копии многоэтажных зданий, имитируя при этом розу ветров,
характерную для той местности, где предполагается их строительство. Пользуются
физическими моделями и в кораблестроении.
2. АНАЛОГОВЫЕ МОДЕЛИ.
Так называют модели, представляющие исследуемый
объект аналогом, который ведет себя как реальный объект, но не выглядит как таковой.
Приведем два достаточно характерных примера.
ПРИМЕР 1. График, иллюстрирующий соотношения между затраченными усилиями и
результатами, является аналоговой моделью. График на рисунке 1 показывает, как
количество времени, отведенное студентом на подготовку к экзамену, влияет на
его результат.

Рисунок 1. Аналоговая
модель.
ПРИМЕР 2. Предположим, что нужно найти наиболее экономичный способ для регулярных
известных поставок товаров в три города, построив для этого только один склад.
Основное требование: место для склада должно быть таким, чтобы полные
транспортные расходы были наименьшими (считается, что стоимость каждой
перевозки равна произведению расстояния от склада до пункта назначения на общий
вес перевозимых товаров и измеряется в тонна-километрах).
Для решения этой задачи наклеим карту местности на
лист фанеры. Затем в месте нахождения каждого города пропилим сквозные
отверстия, пропустим через них нити и привяжем к ним грузики, пропорциональные
запросам товаров в этот город (рисунок 2). Свяжем свободные концы нитей в один
узел и отпустим. Под действием силы тяжести система придет в состояние
равновесия. То место на листе фанеры, которое при этом займет узел, и будет
соответствовать оптимальному расположению склада (рисунок 3).
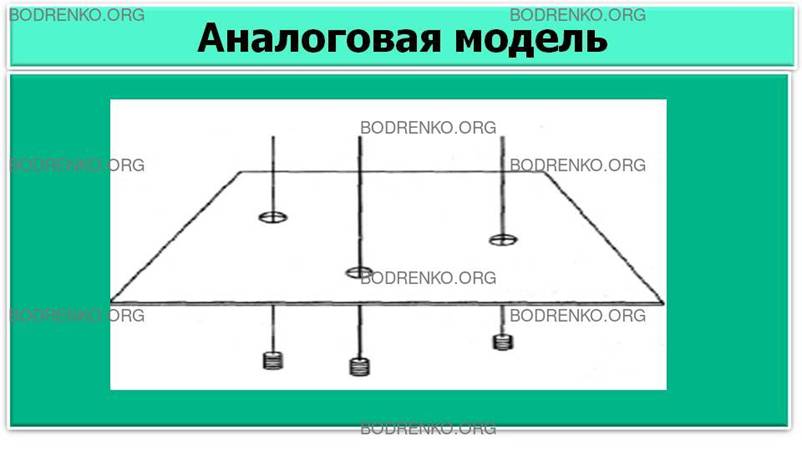
Рисунок 2. Построение аналоговой модели экономичной
перевозки грузов.
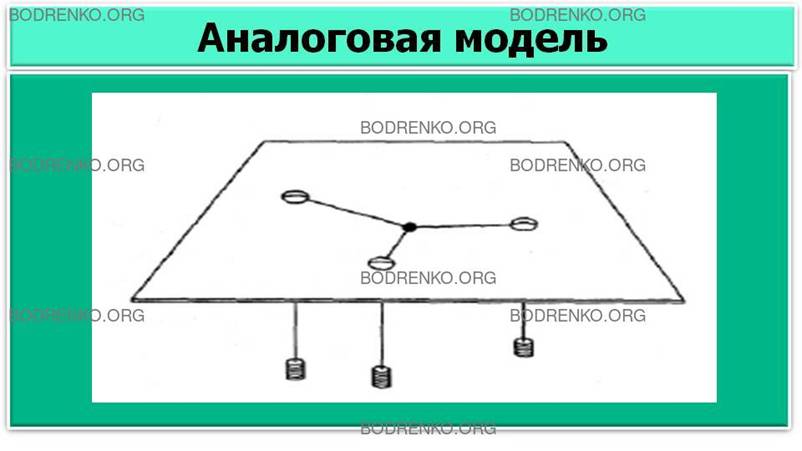
Рисунок 3. Аналоговая модель: оптимальное
расположение склада.
ЗАМЕЧАНИЕ. Стоимость
дорог, которые придется построить заново, мы для простоты рассуждений в расчет
не принимаем.
3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ.
Так называют модели, использующие для описания
свойств и характеристик объекта или события математические символы и методы. Если
некоторую проблему удается перенести на язык формул, то она сильно упрощается.
Математический подход прост еще и потому, что он подчиняется вполне
определенным жестким правилам, которые нельзя отменить указом или иным
способом. Сложность нашей жизни как раз и состоит в том, что многое, что в ней
случается, нередко свободно от пут условностей. Математика имеет дело с
упрощенным описанием явлений. По существу, любая формула (или совокупность
формул) представляет собой определенный этап в построении математической
модели. Опыт показывает, что построить модель (написать уравнение) довольно
легко. Трудно в этой модельной и, следовательно, упрощенной форме суметь
передать суть изучаемого явления.
Динамические математические
модели, хорошо зарекомендовавшие себя в
физике, а затем в биологии, имеют много общего, хотя и сохраняют специфические
особенности каждой из этих наук. Сейчас модели этого класса все шире
применяются в социологии и экономике. К настоящему времени современная
методология анализа нелинейных динамических систем оформилась в новое научное
направление, называемое синергетикой. Эта междисциплинарная наука нацелена на
выявление общих принципов эволюции и самоорганизации сложных систем в различных
областях знания на основе построения и исследования нелинейных динамических
математических моделей. Важными понятиями синергетики являются «катастрофа»,
«бифуркация», «предельный цикл», «странный аттрактор», «диссипативная
структура», «бегущая волна» и т. д. Возникающие при использовании сравнительно
простых нелинейных моделей, эти понятия позволяют нам глубже проникнуть в суть
многих процессов и явлений. Физика, химия, биология в изобилии демонстрируют
примеры успешного применения этой методологии. К ним можно отнести фазовые
переходы между агрегатными состояниями вещества, турбулентные течения жидкости,
структуры в средах при наличии автокаталитических реакций, волны жизни и волны
горения, колебания численности природных популяций и др.
На предыдущих лекциях
мы рассмотрели достаточное число разнообразных
математических моделей, детерминированных, стохастических и игровых. В этом разделе лекции мы приведем примеры
динамических моделей, на основании которых можно делать прогнозы на будущее и
по-новому заглядывать в прошлое. Итак, мы рассматриваем модели, в которые
входят изменяющиеся во времени величины, уделяя основное внимание простейшим из
них.
Дело в том, что сами модельные уравнения (модели)
строятся на основе простых и зачастую почти очевидных соображений. Именно анализ
предлагаемых уравнений позволяет как-то оценить степень их адекватности
описываемым ими обстоятельствам.
МОДЕЛЬ НАРОДОНАСЕЛЕНИЯ.
В 1820 году в Лондоне Т.Р. Мальтусом была опубликована работа «Principles of political economy considered with a
view to their practical application» (в русском переводе: «Опыт о законе народонаселения»).
В этой работе, в частности, говорилось о том, что в
силу биологических особенностей людей население имеет тенденцию размножаться по
закону геометрической прогрессии:
xn+1=γ∙xn, γ>1, (1)
в то
время как средства существования могут увеличиваться лишь по закону
арифметической прогрессии:
yn+1=yn+ d, d>0.

Такое различие в скорости изменения величин,
непосредственно связанных с проблемами выживаемости популяции (рисунок 4), не
могло остаться незамеченным и вызвало довольно жесткую критику и сильно
политизированную полемику в соответствующих кругах.
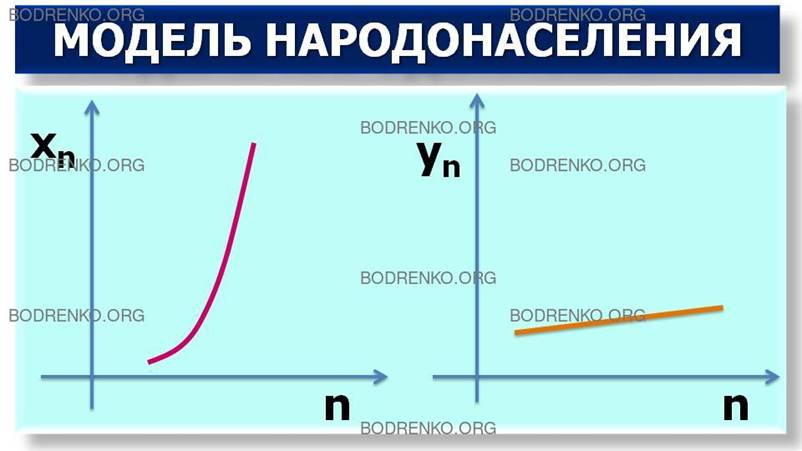
Рисунок 4.
Модель народонаселения Мальтуса.
Попробуем извлечь из самого факта критики полезный
для нас вывод об адекватности построенной модели народонаселения (1).
Разумеется, при попытке упрощенного описания
ситуации некоторыми обстоятельствами приходится пренебрегать, считая их
несущественными. Однако единого взгляда на то, что именно существенно, а что не
очень, по-видимому, нет. Можно, например, не обращать внимания на то, что
начался дождик. Но согласитесь, что одно дело пробежать под накрапывающим
дождем сотню метров, и совсем другое — часовая прогулка под таким дождем без
зонта. Нечто аналогичное мы наблюдаем и здесь: при расчете на 3-4 года вперед
формула (1) работает достаточно хорошо, но долгосрочный прогноз, основанный на
ней, оказывается ошибочным.
ВАЖНЫЙ ВЫВОД. Предлагая построенную или выбранную вами модель, вы
непременно должны указать пределы, в которых ею можно пользоваться, и
предупредить о том, что нарушение этих ограничений может привести (и, скорее
всего, приведет) к серьезным ошибкам. Коротко говоря, у каждой модели есть свой
ресурс. Покупая блузку или рубашку, мы привыкли к наличию меток, на которых
указаны максимально допустимая температура глажения, дозволенные виды стирки и
т. п. Это, конечно, ни в коей мере не означает, что вам запрещается, взяв
докрасна раскаленный утюг, пройтись им раз-другой по ткани. Такое вы сделать
можете. Но вот захотите ли вы носить блузку или рубашку после такого глажения?
В модели народонаселения (1) возможны три различных
случая.
Случай 1. Численность населения растет (рисунок 5).
Случай 2. Численность
населения не изменяется (рисунок 6).
Случай 3. Население
вымирает (рисунок 7).

Рисунок 5. Модель народонаселения (γ>1):
население растет.
Рисунок 6. Модель народонаселения (γ=1):
численность населения не изменяется.
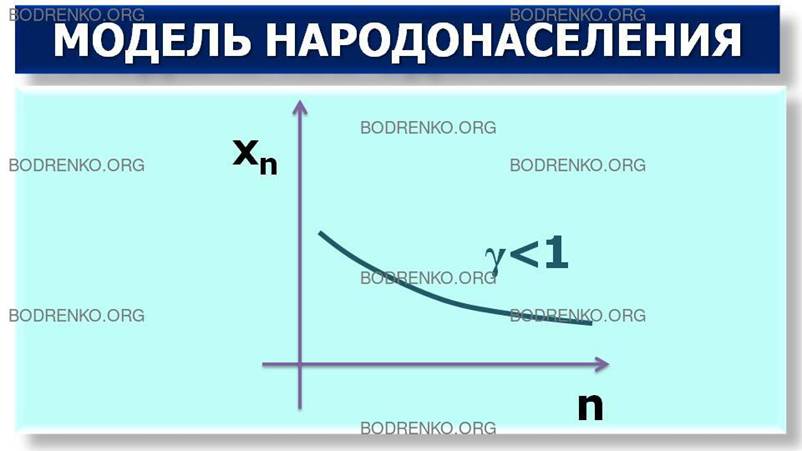
Рисунок 7. Модель народонаселения (γ<1):
население вымирает.
ЗАМЕЧАНИЕ
1. Очень часто, описывая эту модель народонаселения
(1), привлекают ее дифференциальный вариант:
x`=δ∙x,
здесь x=x(t) – зависящая
от времени численность популяции, x` – производная
по времени, δ – постоянная величина.
ЗАМЕЧАНИЕ
2. При больших значениях x конкурентная борьба за средства существования
приводит к уменьшению δ, и эта жесткая модель должна быть заменена более
мягкой моделью:
x`=δ(x)∙x,
в которой
коэффициент δ=δ(x) зависит от численности населения x.
В простейшем
случае эта зависимость описывается так:
δ(x)= a – b∙x ,
где a и b – постоянные
числа, а соответствующее уравнение принимает вид:
x`=(a – b∙x)∙x,

И мы приходим к более сложной, так называемой логистической
модели, которая описывает динамику популяции уже
достаточно хорошо. Анализ логистической кривой (рисунок 8) весьма поучителен.
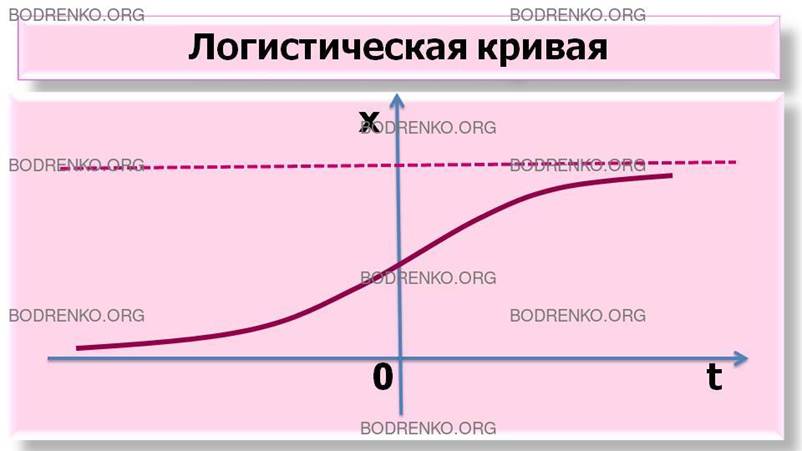
Рисунок 8. Логистическая кривая.
Логистическая модель хорошо описывает и другие
процессы, например, эффективность рекламы.
МОДЕЛЬ МОБИЛИЗАЦИИ.
ЧТО ПОНИМАЕТСЯ ПОД ТЕРМИНОМ МОБИЛИЗАЦИЯ В МОДЕЛИ?
Под термином политическая, или социальная, мобилизация понимается вовлечение людей в партию или в число ее
сторонников, в какое-либо общественное движение и т. п.
Вследствие того что текущий уровень мобилизации
тесно связан с прошлым ее уровнем, а будущая мобилизация зависит от сегодняшних
успехов пропагандистской кампании, ясно, что при построении соответствующей
модели необходимо учитывать временной фактор. Иными словами, нужно понимать,
что искомая модель должна быть динамической.
ПОСТАНОВКА ЗАДАЧИ.
Необходимо
отразить логику изменения уровня мобилизации в данном регионе между двумя
соседними моментами времени, скажем, за месяц (за год, неделю, день и т. п.).
ПОСТРОЕНИЕ МОДЕЛИ.
Примем за
единицу ту часть населения, для которой мобилизация данного типа имеет смысл.
Пусть Mn – доля
мобилизованного населения в момент времени tn=n.
Тогда доля немобилизованного населения будет равна:
1 – Mn
Геометрически
мобилизованное и немобилизованное население можно изобразить в виде двух множеств
следующим образом.

Рисунок 9. Мобилизованное и немобилизованное
население.
За месяц
уровень мобилизации может измениться по двум основным причинам:
1) часть населения удалось привлечь дополнительно;
ясно, что эта величина тем больше, чем выше доля еще несагитированного населения
на момент tn=n, и поэтому можно считать ее равной:
α∙(1 – Mn),
здесь α>0
– коэффициент агитируемости, постоянный для данного региона;
2) часть населения убыла (по разным причинам);
ясно, что это уменьшает долю сагитированного населения тем больше, чем выше была
эта доля на момент tn=n, и поэтому потери, связанные с выбытием, можно
считать равными:
β∙Mn ,
здесь β>0 – постоянный коэффициент выбытия.
Подчеркнем, что числовые параметры α и β отражают
пропорциональное изменение интересов, взглядов и намерений соответствующих
частей населения рассматриваемого региона.
Таким
образом, изменение уровня мобилизации за единицу времени:
ΔMn=Mn+1 – Mn
равно
разности между долей населения, привлеченного дополнительно, и долей выбывшего
сагитированного населения:
Mn+1 – Mn= α∙(1 – Mn) –
β∙ Mn . (2)
Уравнение (2) и есть уравнение процесса мобилизации. Модель мобилизации построена.
Последнее
соотношение легко преобразуется к следующему виду:
Mn+1 = α
+ λ∙Mn , (3)
где
λ=1 – α – β.

ЗАМЕЧАНИЕ. Вспомогательный
параметр λ не может быть больше 1 вследствие того, что исходные параметры α
и β положительны.
Полученное уравнение (3) называется линейным разностным уравнением
с постоянными коэффициентами.
Интересно отметить, что построенная модель, несмотря
на простоту подходов и рассуждений, довольно хорошо отражает реальные процессы.
Так, предложенная модель мобилизации использовалась для изучения динамики числа
голосов, поданных за демократическую партию в Лейк Кантри (США) в 1920-1968
гг., и оказалось, что она достаточно хорошо описывает качественные
характеристики процесса мобилизации.
МОДЕЛЬ ГОНКИ ВООРУЖЕНИЙ.
Рассмотрим конфликтную ситуацию, в которой могут
оказаться две соседние страны, для определенности названные странами X и Y.
Обозначим через x=x(t) расходы
на вооружение страны X и через y=y(t) расходы на вооружение страны Y в момент времени t≥0.
ПРЕДПОЛОЖЕНИЕ
1. Страна X вооружается, опасаясь потенциальной угрозы войны со
стороны страны Y, которая в свою очередь, зная о росте затрат на вооружение
страны X, также
увеличивает свои расходы на вооружение. Каждая страна изменяет скорость роста
(или сокращения) расходов на вооружение пропорционально уровню затрат другой. В
простейшем случае это можно описать так:
x`=μ∙y,
y`=ν∙x,
где μ>0,
ν>0 – положительные постоянные.

Однако написанные уравнения имеют очевидный
недостаток: уровень вооружения ничем не
лимитируется. Поэтому правые части этих уравнений нуждаются в естественной
корректировке.
ПРЕДПОЛОЖЕНИЕ
2. Чем
больше текущий уровень расходов страны на оборону, тем меньше скорость его
роста. Это позволяет внести в предыдущую систему
следующие изменения:
x`=μ∙y –
ρ∙x ,
y`=ν∙x –
τ∙y ,

ПРЕДПОЛОЖЕНИЕ
3. Введем в систему постоянные коэффициенты a и b. Если a и b – положительные постоянные, то эти коэффициенты
интерпретируются как соответствующие
претензии стран. В случае если
постоянные a и b отрицательны, их можно назвать коэффициентами
доброй воли.
Основываясь на всех трех предположениях, в
результате получаем следующую систему уравнений:
x`=μ∙y –
ρ∙x +a,
y`=ν∙x – τ∙y
+b,
Модель гонки вооружений построена.
Решением полученной системы являются функции x(t) и y(t), определяемые
для данных начальных условий x0≥0, y0≥0 (начального состояния гонки вооружений).

ЗАМЕЧАНИЕ. Интересно отметить, что возможности построенной модели проверялись на
реальной ситуации — гонке вооружений перед первой мировой войной. Проведенные
исследования показали, что, несмотря на свою простоту, эта модель достаточно
достоверно описывает положение дел в Европе в 1909-1913 гг.

В завершение описания этой модели процитируем
высказывание Т. Саати об этой модели: «Модель представляется гораздо более
убедительной, если вместо вооружений провести на ней изучение проблем угрозы,
поскольку люди реагируют на абсолютный уровень враждебности, проявляемый по
отношению к ним другими, и испытывают чувство тревоги в степени,
пропорциональной уровню враждебности, которую они испытывают сами».
На следующих лекциях мы подробно рассмотрим линейные динамические модели макроэкономики с дискретным временем и с непрерывным временем. Заключительную лекцию мы посвятим изучению малосекторных нелинейных динамических моделей макроэкономики.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
[1] Бережная
Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб.
пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432
с.: ил.
[2] Колемаев В.А. Экономико-математическое
моделирование. Моделирование
макроэкономических процессов и систем. М.:
ЮНИТИ-ДАНА, 2005. - 295 с.

[3] Красс М.С., Чупрынов Б.П. Основы
математики и ее приложения в экономическом образовании: Учебник. 4-е изд., испр.
– М.: Дело, 2003. – 688 с.
[4] Фомин Г. П.
Математические методы и модели в
коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и
статистика, 2005. — 616 с: ил.
[5] Шикин Е.
В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб.
пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический
университетский учебник»).
