Математическое моделирование экономических систем

 

Лекция 5

 

Тема лекции 5: «Методы и модели прогнозирования временных рядов экономических показателей»

Разделы лекции:

 

1.Основные положения и понятия в прогнозировании временных рядов.

2. Характеристика методов и моделей прогнозирования показателей работы предприятий.

3. Прогнозирование с помощью методов экстраполяции.

РАЗДЕЛ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ И ПОНЯТИЯ В ПРОГНОЗИРОВАНИИ ВРЕМЕННЫХ РЯДОВ.

 

Среди большого разнообразия экономико-математических методов, используемых для решения задач управления предприятием, особое место занимают методы и модели прогнозирования.

 

Следует различать два понятия, связанных с прогнозированием,- предсказание и собственно прогнозирование.

 

Под предсказанием понимают суждение о будущем состоянии процесса, основанное на субъективном «взвешивании» большого числа факторов качественного и количественного характера.

 

Под прогнозом понимается научно обоснованное описание возможных состояний системы в будущем и сроков достижения этих состояний, а процесс разработки прогнозов называют прогнозированием. Прогнозирование — это исследовательский процесс, в результате которого получают прогноз о состоянии объекта. Прогноз является вероятностным суждением о возможном состоянии объекта или об альтернативных путях его достижения. Известно большое количество методов, методик и способов прогнозирования. Все они основаны на двух крайних подходах: эвристическом и математическом.

 

Эвристические методы базируются на использовании явлений или процессов, не поддающихся формализации.

 

Для математических методов прогнозирования характерен подбор и обоснование математической модели исследуемого процесса, а также способов определения ее неизвестных параметров. Задача прогнозирования при этом сводится к решению уравнений, описывающих данную модель для заданного момента времени. В зависимости от объектов прогнозирования прогнозы разделяют на научно-технические, экономические, социальные и т. д.

 

КАК МОЖНО КЛАССИФИЦИРОВАТЬ ЭКОНОМИЧЕСКИЕ ПРОГНОЗЫ?

 

В зависимости от масштабности объекта прогнозирования экономические прогнозы охватывают все уровни: от прогнозов отдельных предприятий и производств (микроуровни) до прогнозов развития отрасли в масштабе страны (макроуровень) или закономерностей мирового масштаба (глобальный уровень).

 

ЧТО ТАКОЕ ВРЕМЯ УПРЕЖДЕНИЯ ПРИ ПРОГНОЗИРОВАНИИ?

 

ОПРЕДЕЛЕНИЕ 1. Временем упреждения (или периодом упреждения, периодом прогноза) при прогнозировании называют отрезок времени от момента, для которого имеются последние данные об изучаемом объекте, до момента, к которому относится прогноз.

 

КАКИЕ ВИДЫ ПРОГНОЗОВ РАЗЛИЧАЮТ В ЭКОНОМИКЕ?

 

По длительности времени упреждения  в экономике различают следующие виды прогнозов:

 

-  оперативные — с периодом упреждения до одного месяца;

 

- краткосрочные — до одного года;

 

-  среднесрочные — от одного года до пяти лет;

 

-  долгосрочные — с периодом упреждения более пяти лет.

 

Наибольший практический интерес представляют оперативные и краткосрочные прогнозы.

Результаты экстраполяции наиболее надежны при кратко- и среднесрочном прогнозировании. При этом предполагается, что совокупность факторов, определявших тенденцию временного ряда в прошлом, в среднем сохранит свою силу и направление действия в течение прогнозируемого периода.

 

ИЗ КАКИХ ЭТАПОВ СОСТОИТ ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ?

 

Прогнозирование экономических процессов состоит из следующих этапов:

 

Этап 1. Постановка задачи и сбор необходимой для прогнозирования информации.

 

Этап 2. Первичная обработка исходной информации.

 

Этап 3. Определение возможных моделей прогнозирования.

 

Этап 4. Оценка параметров рассматриваемых моделей.

 

Этап 5. Проверка адекватности выбранных моделей.

 

Этап 6. Расчет характеристик моделей.

 

Этап 7.Анализ полученных результатов прогноза.

 

Среди математических методов прогнозирования в особую группу выделяются методы экстраполяции, которые отличаются простотой, наглядностью и легко реализуются на ЭВМ. Методологическая предпосылка экстраполяции состоит в признании преимущественной связи между прошлым, настоящим и будущим. При этом развитие экономических явлений наиболее полно находит свое отражение во временных рядах, которые представляют собой упорядоченные во времени наборы измерений каких-либо характеристик исследуемого объекта, процесса. Поэтому независимая переменная для временного ряда, это, как правило, календарные равные отрезки времени (год, квартал, месяц и т. д.).

 

ВИДЫ ВРЕМЕННЫХ РЯДОВ.

 

Происходящие в экономических системах процессы в основном проявляются как ряд расположенных в хронологическом порядке значений определенного показателя, который в своем изменении несет определенную информацию о динамике изучаемого явления.

 

ЧТО ТАКОЕ ВРЕМЕННОЙ РЯД (ДИНАМИЧЕСКИЙ РЯД)?

 

ОПРЕДЕЛЕНИЕ 2. Ряд наблюдений за значениями определенного показателя, упорядоченный в зависимости от возрастающих или убывающих значений другого показателя, называют временным рядом (или динамическим рядом,  рядом динамики).

 

ЧТО ТАКОЕ УРОВНИ ВРЕМЕННОГО РЯДА?

 

ОПРЕДЕЛЕНИЕ 3. Отдельные наблюдения временного ряда называются уровнями этого ряда.

 

КАКИЕ ВРЕМЕННЫЕ РЯДЫ РАЗЛИЧАЮТ? 

 

Временные ряды бывают моментные, интервальные и производные.

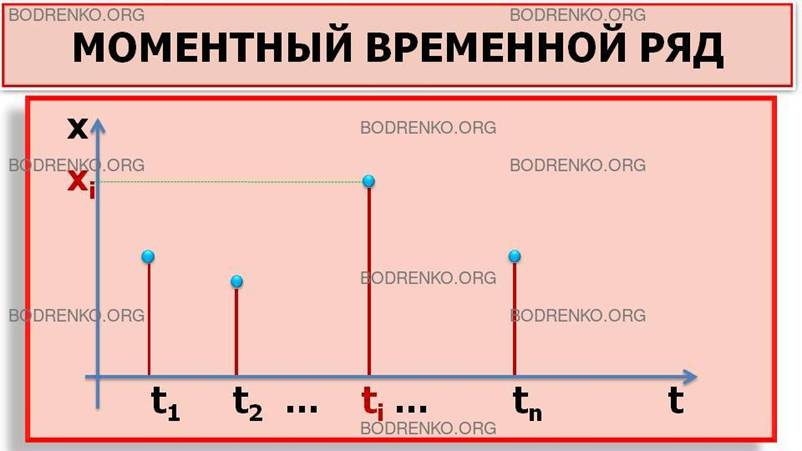
Моментные ряды характеризуют значения показателя на определенные моменты времени; пример такого ряда представлен в таблице 1.

Таблица 1. Численность работников фирмы.

 

Дата	01.01.2011	01.01.2012	01.01.2013	01.01.2014	01.01.2015	01.01.2016
Численность работников, чел.	282	286	294	297	307	295

Интервальные ряды характеризуют значения показателя за определенные интервалы времени. Пример интервального ряда представлен в таблице 2.

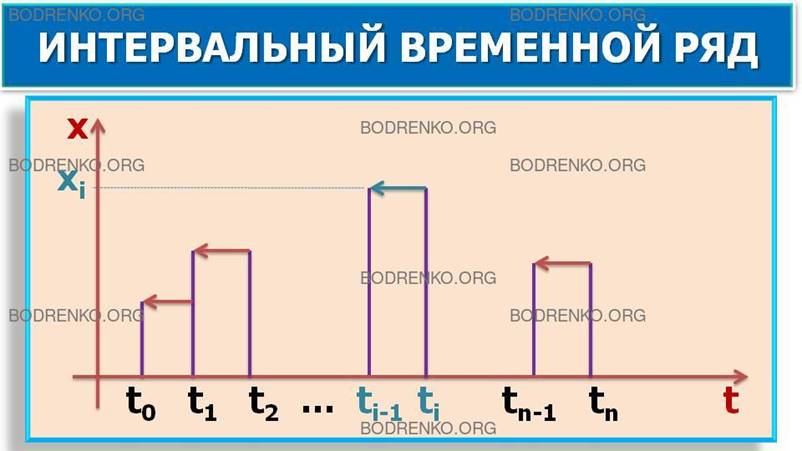
Таблица 2. Фонд заработной платы работников фирмы.

 

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь
Фонд заработной платы, руб.	3 540 000	3 658 000	3 687 500	3 746 500	3 776 000	3 805 500

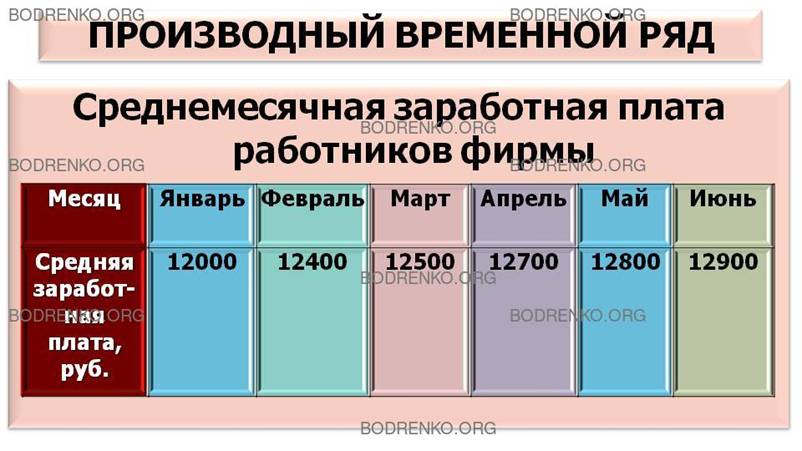
Производные ряды получаются из средних или относительных величин показателя. Пример производного временного ряда представлен в таблице 3.

 

Таблица 3. Среднемесячная заработная плата работников фирмы.

 

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь
Средняя заработная плата, руб.	12 000	12 400	12 500	12 700	12 800	12 900

Основной чертой, выделяющей временные ряды среди других видов статистических данных, является существенность порядка, в котором производятся наблюдения. В ходе решения задачи прогнозирования пользуются ограниченным количеством информации об одномерном временном ряде конечной длины.

 

Уровни ряда могут иметь детерминированные или случайные значения. Ряд последовательных данных о количестве дней в месяце, квартале, году являются примерами рядов с детерминированными значениями. Прогнозированию подвергаются ряды со случайными значениями уровней. Каждый показатель таких рядов может иметь дискретную или непрерывную величину.

 

ТРЕБОВАНИЯ К ИСХОДНОЙ ИНФОРМАЦИИ.

 

Важное значение для прогнозирования имеет выбор интервалов между соседними уровнями ряда. При слишком большом интервале времени могут быть упущены некоторые закономерности в динамике показателя. При слишком малом — увеличивается объем вычислений, могут появляться несущественные детали в динамике процесса. Выбор интервала времени между уровнями ряда должен решаться конкретно для каждого процесса, причем удобнее иметь равноотстоящие друг от друга уровни. Важным условием правильного отражения временным рядом реального процесса развития является сопоставимость уровней ряда. Несопоставимость чаще всего встречается в стоимостных характеристиках, изменениях цен, территориальных изменениях, укрупнения предприятий и др. Для несопоставимых величин показателя неправомерно проводить его прогнозирование. Для успешного изучения динамики процесса необходимо, чтобы информация была полной на принятом уровне наблюдений, временной ряд имел достаточную длину, отсутствовали пропущенные наблюдения.

 

Уровни временных рядов могут иметь аномальные значения. Появление таких значений может быть вызвано ошибками при сборе, записи или передаче информации — это ошибки технического порядка, или ошибки первого рода. Однако аномальные значения могут отражать реальные процессы, например, скачок курса доллара или падение курса ценных бумаг на фондовом рынке и др.; такие аномальные значения относят к ошибкам второго рода, они не подлежат устранению. Для выявления аномальных уровней временных рядов можно использовать метод Ирвина.

 

В ЧЕМ СОСТОИТ МЕТОД ИРВИНА?

 

Пусть имеется временной ряд

 

y₁, y₂, …, y_t, …, y_n, t=1, …,n.   (1)

 

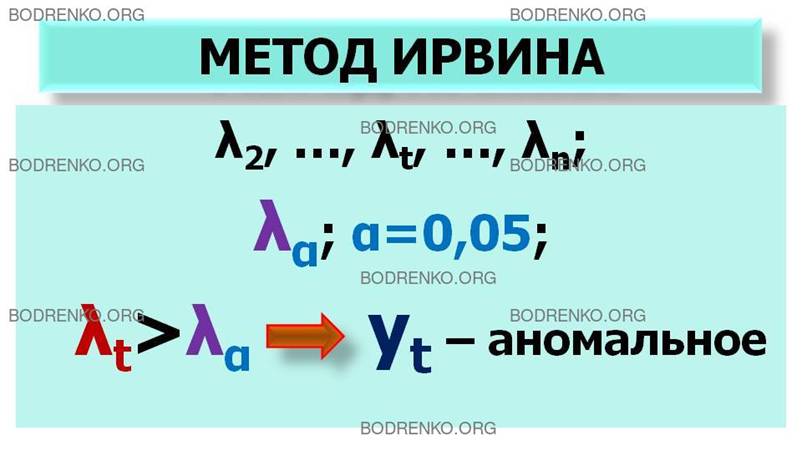
Метод Ирвина предполагает использование следующей формулы:

 

λ_t+1=|y_t+1 – y_t|/σ_y, t=1,2, …

 

где σ_y   –  среднее квадратическое отклонение временного ряда   (1).

Расчетные значения λ₂,  λ₃, …, сравниваются с табличными значениями критерия Ирвина λ_α; если какое-либо из них оказывается больше табличного, то соответствующее значение y_t уровня ряда считается аномальным.

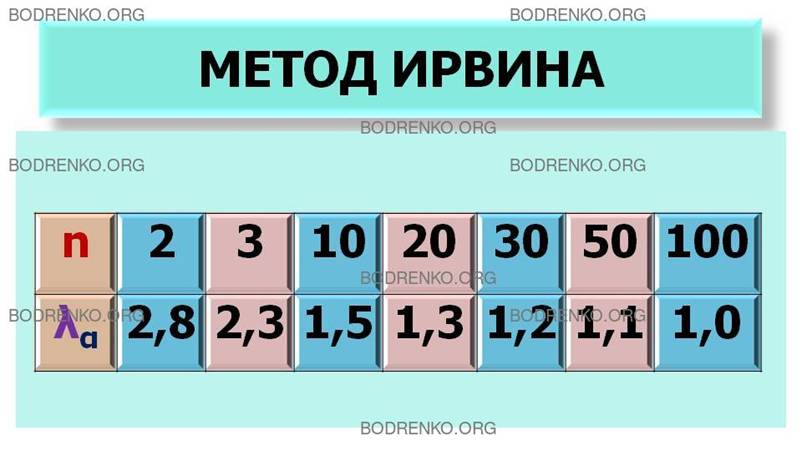
Значения критерия Ирвина для уровня значимости α=0,05 приведены в таблице 4.

 

Таблица 4. Значения критерия Ирвина.

 

n	2	3	10	20	30	50	100
λα	2,8	2,3	1,5	1,3	1,2	1,1	1,0

После выявления аномальных уровней необходимо определить причины их возникновения. Если они вызваны ошибками технического порядка, то они устраняются либо заменой аномальных уровней соответствующими значениями по кривой, аппроксимирующей времен-

ной ряд, либо заменой уровней средней арифметической двух соседних уровней ряда.

 

Ошибки, возникающие из-за воздействия факторов, имеющих объективный характер, устранению не подлежат.

 

КОМПОНЕНТЫ ВРЕМЕННЫХ РЯДОВ.

 

Если во временном ряду проявляется длительная тенденция изменения экономического показателя, то в этом случае говорят, что имеет место тренд. Под трендом понимают изменение, определяющее общее направление развития или основную тенденцию временного ряда.

 

Тренд относят к систематической составляющей долговременного действия. Во временных рядах часто происходят регулярные колебания, которые относятся к периодическим составляющим рядов экономических процессов.

 

ИЗ КАКИХ СОСТАВЛЯЮЩИХ СКЛАДЫВАЮТСЯ ЗНАЧЕНИЯ УРОВНЕЙ ВРЕМЕННЫХ РЯДОВ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ?

 

Считают, что значения уровней временных рядов экономических показателей складываются из следующих составляющих (компонентов):

 

- тренда,

 

- сезонной составляющей,

 

- циклической составляющей  и

 

- случайной составляющей.

КАКИЕ КОЛЕБАНИЯ НАЗЫВАЮТСЯ СЕЗОННЫМИ, ЦИКЛИЧЕСКИМИ?

 

Если период колебаний не превышает года, то их называют сезонными, более года — циклическими составляющими. Чаще всего причиной сезонных колебаний являются природные, климатические условия, циклических — демографические циклы и др.

 

КАКИЕ КОМПОНЕНТЫ ВРЕМЕННОГО РЯДА НАЗЫВАЮТСЯ РЕГУЛЯРНЫМИ?

 

ОПРЕДЕЛЕНИЕ 4. Тренд, сезонная и циклическая составляющие называются регулярными (или систематическими) компонентами временного ряда.

 

Если из временного ряда удалить регулярные компоненты, то останется случайный компонент.

 

КАКАЯ МОДЕЛЬ НАЗЫВАЕТСЯ АДДИТИВНОЙ?

 

Если временной ряд представлен в виде суммы составляющих компонентов, то модель называется аддитивной. Форма записи аддитивной модели следующая.

 

y_t=u_t+s_t+v_t+e_t.

 

Где использованы следующие обозначения:

 

y_t  – уровни временного ряда,

 

u_t – временной тренд,

 

s_t –  сезонный компонент,

 

vt – циклическая составляющая,

 

e_t –  случайный компонент.

 

КАКАЯ МОДЕЛЬ НАЗЫВАЕТСЯ МУЛЬТИПЛИКАТИВНОЙ?

 

Если временной ряд представлен в виде произведения составляющих компонентов, то модель называется мультипликативной. Форма записи мультипликативной модели следующая.

 

y_t=u_t∙s_t∙v_t∙e_t.

 

где

 

y_t  – уровни временного ряда,

 

u_t – временной тренд,

 

s_t –  сезонный компонент,

 

v_t – циклическая составляющая,

 

e_t –  случайный компонент.

 

В КАКОЙ ФОРМЕ ЗАПИСЫВАЕТСЯ МОДЕЛЬ СМЕШАННОГО ТИПА?

 

Модель смешанного типа записывается в следующей форме.

 

y_t=u_t∙s_t∙v_t + e_t.

ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.

 

Прогнозирование временных рядов целесообразно начинать с построения графика исследуемого показателя. Однако в нем не всегда прослеживается присутствие тренда. Поэтому в этих случаях необходимо выяснить, существует ли тенденция во временном ряду или она отсутствует.

 

КАК МОЖНО ПРОВЕРИТЬ СУЩЕСТВОВАНИЕ ТРЕНДА ВРЕМЕННОГО РЯДА?

 

Для временного ряда (1) рассмотрим критерий «восходящих и нисходящих» серий, согласно которому тенденция определяется по следующему алгоритму:

 

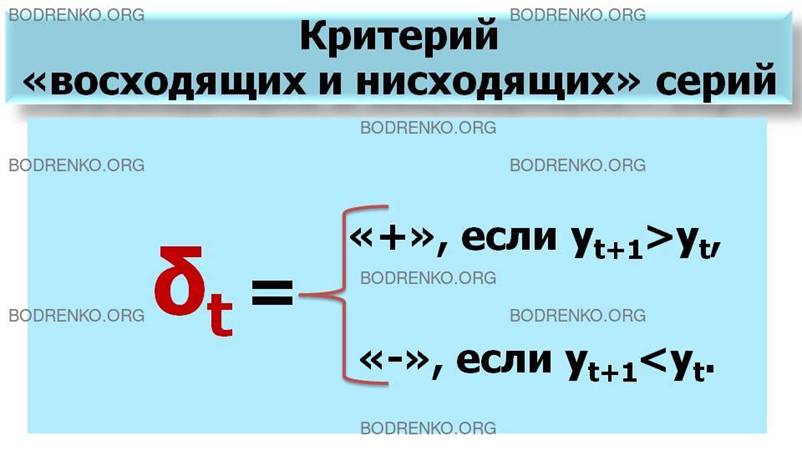
Шаг 1. Для исследуемого временного ряда определяется последовательность знаков, исходя из условий

 

δ_t= «+», если y_t+1>y_t,

 

δ_t= «-», если y_t+1<y_t,

 

При этом, если последующее наблюдение равно предыдущему, то учитывается только одно наблюдение.

Шаг 2. Подсчитывается число серий v(n). Под серией понимается последовательность подряд расположенных плюсов или минусов, причем один плюс или один минус считается серией.

 

Шаг 3. Определяется протяженность самой длинной серии l_max(n).

 

Шаг 4. По таблице 5, приведенной ниже, находится значение l(n).

Таблица 5.

 

Длина временного ряда n	n≤26	26<n≤153	153<n<170
Значение l(n)	5	6	7

Шаг 5. Если нарушается хотя бы одно из следующих двух неравенств, то гипотеза об отсутствии тренда отвергается с доверительной вероятностью 0,95:

 

v(n)>[(2n – 1)/3 – 1,96∙√((16n – 29)/90)],

 

l_max(n)≤l(n),

 

где квадратные скобки в правой части первого неравенства означают целую часть числа.

ПРИМЕР 1.

 

Дана динамика ежеквартального выпуска продукции фирмы в денежных единицах. С помощью критерия «восходящих и нисходящих» серий сделать вывод о присутствии или отсутствии тренда. Доверительную вероятность принять равной 0,95.

 

t	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
yt	9	13	6	15	14	16	15	19	16	6	14	15	19	13	18	20

РЕШЕНИЕ.

 

Шаг 1. Определим последовательность знаков. Результаты запишем в следующую таблицу.

 

t	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
yt	9	13	6	15	14	16	15	19	16	6	14	15	19	13	18	20
δt		+	-	+	-	+	-	+	-	-	+	+	+	-	+	+

Шаг 2.  Подсчитаем число серий. Число серий v(n)=11.

 

Шаг 3. Определим протяженность самой длинной серии l_max(n)=3.

 

Шаг 4. По таблице 5 находим значение l(n)=5.

 

Шаг 5. Запишем систему неравенств, подставив данные задачи:

 

11>[(32 – 1)/3 – 1,96∙√((256 – 29)/90)],

 

3≤5.

 

Отсюда, имеем систему неравенств:

 

11>7,

 

3≤5.

ВЫВОД. Оба неравенства выполняются, поэтому тренд в динамике выпуска продукции фирмы отсутствует с доверительной вероятностью 0,95.

 

СГЛАЖИВАНИЕ ВРЕМЕННЫХ РЯДОВ.

 

Предварительный анализ временных рядов экономических показателей заключается в выявлении аномальных значений уровней ряда, которые не соответствуют реальным возможностям рассматриваемой экономической системы, а также в определении наличия тренда. Наиболее распространенным приемом для устранения аномальных значений показателей и отсутствия тенденции временного ряда является сглаживание временного ряда. При этом производится замена фактических уровней временного ряда расчетными, что способствует более четкому проявлению тенденции ряда. Сглаживание временного ряда является одним из методов теории математических фильтров, имеющей дело с фильтрацией высокочастотных «шумов». Скользящие средние позволяют сгладить случайные и периодические колебания временного ряда.

 

СГЛАЖИВАНИЕ ПО ПРОСТОЙ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ.

 

Наиболее распространенной процедурой сглаживания является метод простой скользящей средней. Сначала для временного ряда определяется интервал сглаживания (g). Если необходимо сгладить мелкие колебания, то интервал сглаживания берут по возможности большим, если нужно сохранить более мелкие колебания, то интервал сглаживания уменьшают. Для первых (g) уровней временного ряда вычисляется их среднее арифметическое значение. Это будет сглаженное значение уровня ряда, находящегося в середине интервала сглаживания.

 

Затем интервал сглаживания сдвигается на один уровень вправо, повторяется вычисление средней арифметической и т. д. В результате такой процедуры получим ряд сглаженных значений, при этом в зависимости от (g) первые и последние уровни теряются.

 

Длину интервала сглаживания (g) удобно брать в виде нечетного числа, в этом случае расчетное значение скользящей средней будет приходиться на средний интервал ряда. Например, для интервала g=3 сглаженные уровни рассчитываются по формуле:

 

ŷ_t=(y_t-1+y_t+y_t+1)/3.

 

Для того чтобы не потерять первый и последний уровни ряда, их можно вычислить по формулам параболического интерполирования:

 

ŷ₁=(5y₁+2y₂ - y₃)/6.

 

ŷ_n=(-y_n-2+2y_n-1+5y_n)/6.

 

Метод простой скользящей средней дает хорошие результаты в динамических рядах с линейной тенденцией развития.

СГЛАЖИВАНИЕ С ИСПОЛЬЗОВАНИЕМ ВЗВЕШЕННОЙ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ.

 

Для рядов с нелинейной тенденцией развития необходимо применять метод взвешенной скользящей средней. Этот метод отличается от метода простой скользящей средней тем, что уровни, входящие в интервал сглаживания, суммируются с разными весами.

 

Например, для полиномов 2-го и 3-го порядков по 5-членной взвешенной скользящей средней центральное значение интервала определяется по формуле:

 

ŷ_t=(-3y_t-2+12y_t-1+17y_t +12y_t+1 -3y_t+2)/35.

ЭКСПОНЕНЦИАЛЬНОЕ СГЛАЖИВАНИЕ.

 

Суть метода заключается в том, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное значение уровня ряда.

 

РАЗДЕЛ 2. ХАРАКТЕРИСТИКА МЕТОДОВ И МОДЕЛЕЙ ПРОГНОЗИРОВАНИЯ ПОКАЗАТЕЛЕЙ РАБОТЫ ПРЕДПРИЯТИЙ.

 

В экономической литературе предлагается широкий спектр методов экстраполяции. Остановимся на краткой характеристике основных методов данной группы.

 

КАКИЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ МОЖНО ВЫДЕЛИТЬ?

 

 В настоящее время разработана большая группа экстраполяционных методов прогнозирования отдельных экономических показателей.

 

В данной группе методов можно выделить следующие:

 

1. Методы, основанные на построении многофакторных корреляционно-регрессионных моделей;

 

2. Методы  авторегрессии, учитывающие взаимосвязь членов временного ряда.

 

3. Методы, основанные на разложении временного ряда на компоненты: главная тенденция (тренд), сезонные колебания, циклические колебания и случайная составляющая;

 

4. Методы, позволяющие учесть неравнозначность исходных данных.

 

5. Методы  прямой экстраполяции, при этом используются разные трендовые модели.

 

Коротко охарактеризуем эти методы.

 

1. При прогнозировании методом корреляционно-регрессионного анализа строится модель, включающая набор переменных, от которых зависит поведение функции. Основным недостатком этого подхода является то, что необходимы сбор и обработка больших массивов информации по группе однородных предприятий и прогнозирование самих объясняющих

переменных. При этом остается открытым вопрос о прогнозировании показателей работы предприятий, не вошедших в группу однородных. Для данных методов характерна невысокая точность прогноза для конкретного, отдельного предприятия.

 

В КАКИХ СЛУЧАЯХ ПРИМЕНЯЮТСЯ МЕТОДЫ АВТОРЕГРЕССИИ?

 

2. Авторегрессионные модели чаще всего используются для прогнозирования тех экономических процессов, для которых внешний механизм их формирования четко не определен, и практически невозможно выделить стабильные во времени причинно-следственные связи. Применение этих моделей целесообразно и для сильно автокоррелированных динамических рядов. Главная идея методов авторегрессии состоит в том, что будущие значения временного ряда не могут произвольно отклоняться в большую или меньшую сторону от предшествующих значений  временного ряда, какими бы причинами ни были вызваны эти отклонения. Во временных рядах экономических показателей существует связь между недавно реализованными значениями и значением, реализующимся в близком будущем. Смысл этой связи таков, что если между близкими значениями временного ряда существует корреляция, то можно построить прогноз показателя.  Для улучшения прогнозирующих свойств модели авторегрессии в нее можно ввести фактор времени в виде самостоятельной переменной. Подобный подход в ряде случаев существенно увеличивает точность прогноза, что объясняется учетом линейного тренда.

 

3. Методы, основанные на разложении временного ряда на компоненты – главная тенденция, сезонные колебания и случайная составляющая, – позволяют описать почти любой экономический  процесс, независимо от его характера.

 

Рассмотренные выше методы не позволяют в достаточной степени учесть неравнозначность исходных данных.

 

КАКИЕ МЕТОДЫ ПОЗВОЛЯЮТ УЧЕСТЬ НЕРАВНОЗНАЧНОСТЬ ИСХОДНЫХ  ДАННЫХ?

 

4. К числу методов, учитывающих неравнозначность данных, можно отнести:

 

-  метод авторегрессии с последующей адаптацией коэффициентов уравнения;

 

- метод взвешенных отклонений.

 

Для адаптации коэффициентов модели авторегрессии может быть использован метод наискорейшего спуска.  Заметим, что адаптация производится либо по последнему эмпирическому значению, либо по предыдущему производному значению.

 

Метод взвешенных отклонений достаточно подробно изложен в работе Л. Г. Лабскера, Л. О. Бабешко «Теория массового обслуживания в экономической сфере». Для сравнения точности прогнозных оценок, получаемых с использованием рассмотренных выше методов, был произведен ретроспективный прогноз показателей работы подвижного состава десяти транспортных предприятий. Объем выборки составил более 857 вариантов расчетов. Средние ошибки приведены в таблице 6.

 

Таблица 6. Модели прогнозирования показателей работы автомобилей.

 

 

№ п/п	Наименование модели прогнозирования	Средняя ошибка прогноза, %
1.	Авторегрессия без учета времени	1,89
2.	Авторегрессия с учетом времени	2,94
3.	«Гармонический фильтр» без учета значимости	1,9
4.	«Гармонический фильтр» с учетом значимости	2,34
5.	Метод взвешенных отклонений	2,24
6.	Авторегрессия без учета времени и с последующей адаптацией параметров модели	1,82
7.	Авторегрессия с учетом времени и последующей адаптацией параметров модели	1,94

 

Анализ ошибок (таблица 6) позволяет сделать следующие выводы.

 

Все модели прогнозирования обладают достаточно высокой точностью. Наиболее точным методом прогнозирования показателей работы транспортных предприятий является авторегрессия без учета фактора времени и с последующей адаптацией коэффициентов данной модели (средняя ошибка =1,82%).

 

ЗАМЕЧАНИЕ. Модель авторегрессии без учета фактора времени и с последующей адаптацией коэффициентов данной модели в отдельных случаях может значительно уступать по точности другим моделям прогнозирования. Например, при прогнозировании показателя балансовой прибыли ошибка прогноза оказалась в 2,61 раза больше, чем ошибка прогноза, полученного с использованием метода взвешенных отклонений. Общее число случаев, когда модель авторегрессии без учета времени и с последующей адаптацией коэффициентов данной модели оказалась лучшей по точности, составило 67%. Поэтому для прогнозирования экономических показателей работы предприятий необходимо использовать комплекс моделей прогнозирования, приведенных в таблице 6. Сложность математического аппарата моделей прогнозирования, представленных в таблице 6, не оправдывает себя. Для получения точных оценок прогнозирования в каждом случае необходимо использовать эти модели прогнозирования в комплексе, что значительно увеличивает время на получение прогноза.

 

Проведенные исследования показали, что при краткосрочном прогнозировании (на один год) показателей работы предприятий целесообразно использовать комплекс трендовых моделей, который позволяет с достаточной точностью описать динамику показателей. В связи с вышеизложенным остановимся более детально на процедуре прогнозирования с помощью прямой экстраполяции.

 

РАЗДЕЛ 3. ПРОГНОЗИРОВАНИЕ С ПОМОЩЬЮ МЕТОДОВ ЭКСТРАПОЛЯЦИИ.

 

Прогнозирование с помощью методов экстраполяции должно включать следующие этапы работ.

 

ЭТАП 1. УСТАНОВЛЕНИЕ ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ, АНАЛИЗ ОБЪЕКТА ПРОГНОЗИРОВАНИЯ.

 

Прогнозирование развития любой системы (предприятия, фирмы и т. д.) предъявляет специфические требования к параметрам (объектам), характеризующим и определяющим ее развитие. Поэтому необходимо на первом этапе работ провести детальное логическое изучение системы: зависимость рассматриваемого объекта (параметра, показателя) от других систем одного уровня и субсистемы (системы более высокого уровня); взаимосвязь между данным объектом и другими объектами системы; установление характера предоставления статистических данных об объекте.

 

ЭТАП 2. ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ.

 

Работы по этому этапу начинаются с проверки временного ряда, в результате которой устанавливаются полнота ряда (наличие данных за каждый год (месяц, квартал) ретроспективного периода), сопоставимость данных и, в случае необходимости, проверка методики приведения данных к сопоставимому виду. Если временной ряд представлен не полностью, то необходимо недостающие данные определить с помощью тех или иных методов интерполяции в зависимости от характера протекания процесса. Наряду с этим осуществляется также формирование массива функций, который в последующем будет использован для выбора вида математической модели.

 

ЭТАП 2. ФИЛЬТРАЦИЯ ИСХОДНОГО ВРЕМЕННОГО РЯДА.

 

В результате этой процедуры устраняются случайные возмущения (флуктуации), возникающие под воздействием неучтенных факторов или ошибок измерения относительно наиболее вероятного протекания процесса, и тем самым исключается искажающее влияние случайных колебаний на выбор вида регрессии.

 

КАКИЕ ПРОЦЕДУРЫ ВКЛЮЧАЕТ ФИЛЬТРАЦИЯ ИСХОДНОГО ВРЕМЕННОГО РЯДА?

 

Фильтрация исходного динамического ряда включает его сглаживание и выравнивание.

ДЛЯ ЧЕГО ПРИМЕНЯЕТСЯ СГЛАЖИВАНИЕ?

 

Сглаживание применяется для устранения случайных отклонений (шума) из экспериментальных значений исходного ряда. Сглаживание производится с помощью многочленов, приближающих (обычно по методу наименьших квадратов) группы опытных точек. Наилучшее сглаживание получается для средних точек группы, поэтому желательно выбирать нечетное количество точек в сглаживаемой группе. Обычно их выбирают три или пять. Например, по первым трем точкам y1, у2, y3  сглаживают среднюю y2, затем по следующей тройке y2, y3, y4 сглаживают у3 и т. д. Крайние точки сглаживают по специальным формулам. Чаще всего для сглаживания применяют линейную зависимость.

 

Сглаживание (даже в простом линейном варианте) является во многих случаях эффективным средством выявления тренда при наличии в экспериментальных точках случайных помех и ошибок измерения.

 

ДЛЯ ЧЕГО ПРИМЕНЯЕТСЯ ВЫРАВНИВАНИЕ?

 

Выравнивание применяется для более удобного представления исходного ряда без изменения его числовых значений. Выравниванием называется приведение исходной эмпирической формулы:

 

y=f(t, a, b)   (*)

 

где t – время,

 

a, b – параметры,

 

к виду

 

Y=a₁∙T+b₁.

ЗАМЕЧАНИЕ. Использование двухпараметрической зависимости (*) объясняется ее наибольшим распространением в практике прогнозирования и сравнительно простыми способами получения выравниваемых формул. Функции с большим (более 2) числом параметров выравниваются не всегда, и формулы имеют громоздкий вид.

 

КАКИЕ СПОСОБЫ ВЫРАВНИВАНИЯ НАИБОЛЕЕ РАСПРОСТРАНЕНЫ?

 

Наиболее распространенными способами выравнивания являются логарифмирование и замена переменных.

 

ПРИМЕР. Дана исходная функция

 

y=a∙t^b.

 

Логарифмируя, получим lg y = lg a + b∙lg t.

 

Вводя замену переменных, имеем:

 

Y= lg y;

 

T= lg t;

 

a₁=lg a;

 

b₁=b.

 

Таким образом, приходим к уравнению:

 

Y=a₁∙T+b₁.

 

В новых переменных мы получим линейную зависимость, с которой легче работать и определять коэффициенты. Затем нужно пересчитать результаты по формулам, обратным исходному преобразованию.

 

ЗАМЕЧАНИЕ. Можно рассматривать выравнивание не как метод представления исходного динамического ряда, а как метод непосредственного приближенного определения параметров аппроксимирующей функции, что часто и делается на практике.

 

ЭТАП 4. ЛОГИЧЕСКИЙ ОТБОР ВИДОВ АППРОКСИМИРУЮЩЕЙ ФУНКЦИИ.

 

На основе изучения статистических данных и логического анализа протекания изучаемого процесса из заданного массива функций отбираются наиболее приемлемые виды уравнений связи. Этот этап необходим, так как позволяет при отборе функций учесть основные условия протекания рассматриваемого процесса и требования, предъявляемые к математической модели. На этом этапе должны быть решены следующие вопросы:

 

1) является ли исследуемый показатель величиной, монотонно возрастающей (убывающей), стабильной, периодической, имеющей один или несколько экстремумов;

 

2) ограничен ли показатель сверху или снизу каким-либо пределом;

 

3) имеет ли функция, определяющая процесс, точку перегиба;

 

4) обладает ли анализируемая функция свойством симметричности;

 

5) имеет ли процесс четкое ограничение развития во времени.

 

КАКИЕ ФУНКЦИИ ОБЫЧНО ИСПОЛЬЗУЮТ В ПРОГНОЗНОЙ ЭКСТРАПОЛЯЦИИ?

 

Рассмотрим те функции, которые предпочтительно использовать в прогнозной экстраполяции.

 

В качестве аппроксимирующих функций чаще всего используются различные полиномы с ограничением степени полинома.

 

Это

 

- степенной полином:

 

- экспоненциальный полином:

 

 

- гиперболический полином:

 

 

Где использованы следующие обозначения:

 

y – прогнозируемый показатель;

 

t – время;

 

a₀, a₁, a₂, …, a_n – параметры (коэффициенты), подлежащие определению.

 

Опыт применения аппроксимирующих функций для целей прогнозирования показывает, что наиболее простыми (математически) и чаще всего используемыми являются следующие функции:

 

- линейная:

 

y(t)=а+b∙t;

 

- квадратичная:

 

y(t)=a+b∙t+c∙t²;

 

-  степенная:

 

y(t)=a∙t^b;

 

-  экспоненциальная:

 

y(t)=a∙exp{b∙t};

 

-  модифицированная экспонента:

 

y(t)=k – a∙exp{-b∙t};

 

-  гиперболическая:

 

 y(t)=a+ b/(c+t);

 

- логистическая кривая:

 

 y(t)=k – a∙exp{-b∙t};

 

где a, b, c, k – параметры.

Когда это возможно, при выборе вида аппроксимирующей функции прибегают к графическому способу подбора по виду точек временного ряда, расположенных на плоскости y0t. Если по графику подобрать функцию трудно, иногда прибегают к анализу производных от соответствующих видов функций аппроксимации (или разностей Δ1, Δ2, Δ3, ...) соответствующего порядка.

 

Выбирают ту функцию для прогноза, арифметическая средняя для разностного ряда которого будет равна нулю или близка к нулю по абсолютной величине. Окончательное решение о виде аппроксимирующей функции может быть принято после определения ее параметров и верификации прогноза по ретроспективному ряду. Поэтому для прогнозирования используют несколько подходящих аппроксимирующих функций, с тем, чтобы после оценки точности выбрать наиболее подходящую функцию.

 

Прогнозные значения исследуемого показателя определяют путем подстановки в уравнение кривой времени t, соответствующему периоду упреждения. Полученный прогноз называют точечным. В дополнение к точечному прогнозу можно определить границы возможного изменения прогнозируемого показателя, т. е. вычислить интервальный прогноз. При прогнозировании, как правило, в точке прогноза оценивают математическое ожидание процесса (точечный прогноз) и величину интервала, в который с заданной вероятностью попадет прогнозируемое значение процесса (интервальный прогноз).

ЭТАП 5. ОЦЕНКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРОГНОЗИРОВАНИЯ.

 

На этом этапе исследования определяются параметры различных видов аппроксимирующих функций. Наиболее распространенными методами оценки параметров аппроксимирующих зависимостей являются метод наименьших квадратов (МНК) и его модификации, метод экспоненциального сглаживания, метод вероятностного моделирования, метод адаптивного сглаживания.

 

Рассмотрим для примера МНК и метод экспоненциального сглаживания.

 

Метод наименьших квадратов состоит в определении параметров модели тренда, минимизирующих ее отклонение от точек исходного временного ряда.  Классический метод наименьших квадратов предполагает равноценность исходной информации в модели. В реальной же практике будущее поведение процесса в большей степени определяется поздними наблюдениями, чем ранними. Речь идет о дисконтировании, т. е. уменьшении ценности более ранней информации. Дисконтирование учитывают путем введения в модель некоторых весов. Весовые коэффициенты могут быть заданы в числовой форме или в виде функциональной зависимости таким образом, чтобы по мере продвижения в прошлое веса убывали.

 

Метод наименьших квадратов широко применяется при прогнозировании, что объясняется его простотой и легкостью реализации на ЭВМ. К недостаткам МНК можно отнести следующее.

 

Во-первых, модель тренда жестко фиксируется, и с помощью МНК можно получить прогноз на небольшой период упреждения. Поэтому МНК относят к методам краткосрочного прогнозирования.

 

Во-вторых, значительную трудность представляет правильный выбор вида модели, а также обоснование и выбор весов во взвешенном методе наименьших квадратов.

 

Наконец, МНК очень просто реализуется только для линейных и линеаризуемых зависимостей, когда для получения оценок коэффициентов моделей решается система линейных уравнений. Задача значительно усложняется, если для прогноза используется функциональная зависимость, не сводимая к линейной.

 

Метод экспоненциального сглаживания является эффективным и надежным методом среднесрочного прогнозирования. Здесь следует остановиться более подробно на учете важности ретроспективной информации. Практически большее значение для построения прогноза имеет информация, описывающая процесс в моменты времени, стоящие ближе к настоящему (нулевому) моменту времени. Чем дальше мы углубляемся в ретроспекцию, тем менее ценной для прогноза становится информация. Это можно учесть, придавая членам исходного динамического ряда некоторые веса, тем большие, чем ближе находится точка к началу периода прогноза. Это положение лежит в основе метода экспоненциального сглаживания.

Сущность метода заключается в сглаживании исходного динамического ряда взвешенной скользящей средней, веса которой подчиняются экспоненциальному закону (рисунок 1).

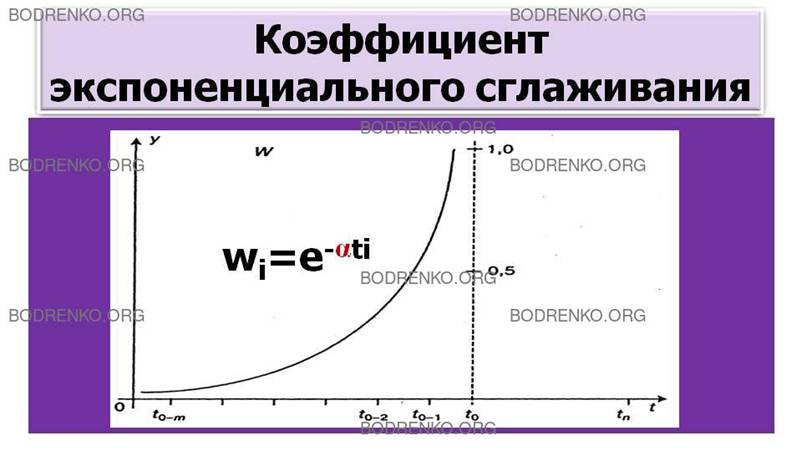
Рисунок 1. Коэффициент экспоненциального сглаживания.

 

Метод экспоненциального сглаживания позволяет построить такое описание процесса, при котором более поздним наблюдениям придаются большие веса по сравнению с ранними наблюдениями, причем веса наблюдений убывают по экспоненте.

 

Для метода экспоненциального сглаживания основным и наиболее трудным моментом является выбор параметра сглаживания α, начальных условий и степени прогнозирующего полинома. Параметр сглаживания α определяет оценки коэффициентов модели, и, следовательно, результаты прогноза.

 

В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного рада наблюдений: чем больше α, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий убывает быстро. При малом α прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более ранней информации происходит медленно.

 

Для приближенной оценки α известны два основных соотношения:

 

1) соотношение Брауна, выведенное из условия равенства скользящей и экспоненциальной средней:

 

α=2/(N+1),

 

где N — число точек ряда, для которых динамика рада считается однородной и устойчивой (число точек в интервале сглаживания).

 

Иногда параметр α принимают равным:

 

α=2/(n+1),

 

где n – число наблюдений (точек) в ретроспективном динамическом раду;

 

2) соотношение Мейера:

 

α=σ_n/σ_ε,

 

где σ_n  - средняя квадратическая ошибка модели;

 

σ_ε,  – средняя квадратическая ошибка исходного ряда.

Однако достоверно определить σ_n и σ_ε,  из исходной информации очень сложно, поэтому использование соотношения Мейера затруднено.

 

Очевидно, что выбор параметра α нужно связывать с точностью прогноза, поэтому для более обоснованного выбора α можно использовать процедуру обобщенного сглаживания. В ряде случаев параметр α выбирают так, чтобы минимизировать ошибку прогноза, рассчитанного по ретроспективной информации.

 

Качество прогноза во многом зависит от выбора порядка прогнозирующего полинома. Известно, что превышение второго порядка модели не приводит к существенному увеличению точности прогноза, но значительно усложняет расчет.

 

Отметим в заключение, что метод экспоненциального сглаживания является одним из наиболее эффективных, надежных и широко применяемых методов прогнозирования. Он позволяет получить оценку параметров тренда, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения, и при этом отличается простотой вычислительных операций.

 

ЭТАП 6. ВЫБОР МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПРОГНОЗИРОВАНИЯ.

 

Выбор моделей прогнозирования базируется на оценке их качества. Независимо от метода оценки параметров моделей экстраполяции (прогнозирования) их качество определяется на основе исследования свойств остаточной компоненты,  т. е. величины расхождений на участке аппроксимации (построения модели) между фактическими уровнями и их расчетными значениями.

 

Качество модели определяется ее адекватностью исследуемому процессу и точностью. Адекватность характеризуется наличием и учетом определенных статистических свойств, а точность — степенью близости к фактическим данным. Модель прогнозирования будет считаться лучшей со статистической точки зрения, если она является адекватной и более точно описывает исходный динамический ряд.

 

КАКАЯ МОДЕЛЬ ПРОГНОЗИРОВАНИЯ СЧИТАЕТСЯ АДЕКВАТНОЙ?

 

Модель прогнозирования считается адекватной, если она учитывает существенную закономерность исследуемого процесса. В ином случае ее нельзя применять для анализа и прогнозирования. Закономерность исследуемого процесса находит отражение в наличии определенных статистических свойств остаточной компоненты, а именно: независимости уровней, их случайности, соответствия нормальному закону распределения и равенства нулю средней ошибки.

 

Независимость остаточной компоненты означает отсутствие автокорреляции между остатками.

 

Перечислим последствия, вызываемые автокорреляцией остатков:

 

1) недооценка дисперсии остатков функции регрессии;

 

2) наличие ошибки при оценке выборочной дисперсии параметров регрессии.

 

Ошибки в вычислении дисперсий — препятствие к корректному применению метода наименьших квадратов при построении модели исходного динамического ряда.

 

Очевидно, важно иметь критерий, позволяющий устанавливать наличие автокорреляции. Таким критерием является критерий Дарбина–Уотсона, в соответствии с которым вычисляется статистика d.  Возможные значения статистики лежат в интервале 0≤d≤4.

 

Согласно методу Дарбина и Уотсона существует верхний dв и нижний dн пределы значений статистики d. Эти критические значения зависят от уровня значимости α, объема выборки n и числа объясняющих переменных m (для трендовых моделей m=1).

 

Критерий Дарбина-Уотсона обладает двумя недостатками. Первый из них — наличие области неопределенности, в которой с помощью данного критерия нельзя прийти ни к какому решению. Второй недостаток заключается в том, что при объеме выборки меньше 15 для d не существует критических значений dн и dв. В этом случае для оценки независимости уровней ряда можно использовать коэффициент автокорреляции r_a.

 

Данный показатель приближенно можно вычислить по формуле:

 

r_a=1 – d/2,

 

где d — статистика Дарбина-Уотсона.

 

Для проверки случайности уровней ряда можно использовать критерий поворотных точек (критерий «восходящих и нисходящих» серий, критерий «пиков» и «впадин»). В соответствии с этим критерием каждый уровень ряда сравнивается с двумя соединенными с ним. Если он больше или меньше их, то эта точка считается поворотной.

 

Соответствие ряда остатков нормальному закону распределения важно с точки зрения правомерности построения интервалов прогноза. Основными свойствами рада остатков являются их симметричность относительно тренда и преобладание малых по абсолютной величине ошибок над большими. В этой связи определяется близость к соответствующим параметрам нормального закона распределения коэффициентов асимметрии Аs (мера «скошенности») и эксцесса Ek (мера «скученности») наблюдений около модели. Если эти коэффициенты близки к нулю или равны нулю, то рад остатков распределен в соответствии с нормальным законом.

 

После проверки всех моделей прогнозирования из выбранного массива на адекватность необходимо выполнить оценку их точности.

 

КАКОВЫ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ТОЧНОСТИ МОДЕЛИ ПРОГНОЗИРОВАНИЯ?

 

В статистическом анализе известно большое число характеристик точности.

 

Наиболее часто в практической работе встречаются следующие характеристики.

 

1. Оценка стандартной ошибки.

 

2. Средняя относительная ошибка оценки.

 

3. Среднее линейное отклонение.

 

4. Ширина доверительного интервала в точке прогноза.

 

Лучшей по точности считается та модель, у которой все перечисленные характеристики имеют меньшую величину. Однако эти показатели по-разному отражают степень точности модели и поэтому нередко дают противоречивые выводы. Для однозначного выбора лучшей модели исследователь должен воспользоваться либо одним основным показателем, либо обобщенным критерием.

 

Итогом работ по выбору вида математической модели прогноза является формирование ее обобщенных характеристик. В обобщенную характеристику должны быть включены вид уравнения регрессии, значения его параметров, оценки точности и адекватности модели и сами прогнозные оценки, точечные и интервальные.

 

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Бережная Е.В., Бережной В.И. Математические методы моделирования экономических  систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с.: ил.

 

 [2] Колемаев В.А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем.  М.: ЮНИТИ-ДАНА, 2005. - 295 с.

[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. 4-е изд., испр. – М.: Дело, 2003. – 688 с.

 

[4] Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

 

[5] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).