Математическое моделирование экономических систем

 

Лекция 4

 

Тема лекции 4: «Методы и модели корреляционно-регрессионного анализа»

Разделы лекции:

 

1. Исходные предпосылки корреляционно-регрессионного анализа.

2. Основные понятия корреляционно-регрессионного анализа.

3. Этапы построения многофакторной корреляционно-регрессионной модели.

РАЗДЕЛ 1. ИСХОДНЫЕ ПРЕДПОСЫЛКИ КОРРЕЛЯЦИОННО-РЕГРЕССИОННОГО АНАЛИЗА.

 

Большинство явлений и процессов в экономике находятся в постоянной взаимной и всеохватывающей объективной связи. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль в экономике. Оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования интенсивности, вида и формы зависимостей широко применяется корреляционно-регрессионный анализ, который является методическим инструментарием при решении задач прогнозирования, планирования и анализа хозяйственной деятельности предприятий.

 

КАКИЕ ВИДЫ ЗАВИСИМОСТЕЙ МЕЖДУ ЭКОНОМИЧЕСКИМИ ЯВЛЕНИЯМИ И ПРОЦЕССАМИ МОЖНО ВЫДЕЛИТЬ?

 

Различают два вида зависимостей между экономическими явлениями и процессами:

 

- функциональную;

- стохастическую (вероятностную, статистическую).

Функциональная зависимость встречается редко. В большинстве случаев функция (Y) или аргумент (X) – случайные величины.

 

Случайные величины X и Y подвержены действию различных случайных факторов, среди которых могут быть факторы, общие для двух случайных величин.

 

ПРИМЕР. Например, если на случайную величину X действуют факторы Z₁, Z₂, ..., V₁, V₂, а на случайную величину Y действуют факторы Z₀, Z₂, V₁, V₃..., то наличие двух общих факторов Z₂ и V₁ позволит говорить о вероятностной или статистической зависимости между случайными величинами X и Y.

ЧТО ТАКОЕ СТАТИСТИЧЕСКАЯ ЗАВИСИМОСТЬ МЕЖДУ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ?

 

ОПРЕДЕЛЕНИЕ. Статистической называется зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины.

В ЧЕМ, В ЧАСТНОСТИ, МОЖЕТ ПРОЯВЛЯТЬСЯ СТАТИСТИЧЕСКАЯ ЗАВИСИМОСТЬ?

 

В частном случае статистическая зависимость проявляется в том, что при изменении одной из величин изменяется математическое ожидание другой. В этом случае говорят о корреляции или корреляционной зависимости. Статистическая зависимость проявляется только в массовом процессе, при большом числе единиц совокупности. При стохастической закономерности для заданных значений зависимой переменной можно указать ряд значений объясняющей переменной, случайно рассеянных в интервале. Каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это обусловливается тем, что зависимая переменная, кроме выделенной переменной, подвержена влиянию ряда неконтролируемых или неучтенных факторов. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.

 

Установление зависимости между двумя или более наблюдаемыми величинами является одним из важных приложений методов математической статистики. При этом наряду с раздельным анализом выборок, составленных из значений этих величин, возможен и их совместный анализ. На лекции мы рассмотрим некоторые методы такого анализа.

 

РАЗДЕЛ 2. ОСНОВНЫЕ ПОНЯТИЯ КОРРЕЛЯЦИОННО-РЕГРЕССИОННОГО АНАЛИЗА.

 

В экономике приходится иметь дело со многими явлениями, имеющими вероятностный характер. Например, к числу случайных величин можно отнести стоимость продукции, доходы предприятия, межремонтный пробег автомобилей, время ремонта оборудования и т. д.

 

Рассмотрим ситуацию, когда в результате эксперимента измеряется не одна, а сразу две случайные величины, скажем X и Y. Примерами здесь могут служить врачебный осмотр, где у каждого пациента измеряют рост и вес; измерение средней температуры воздуха в двух городах в течение определенного дня; проверка квалификации рабочих, когда фиксируются производительность и стаж работы.

 

Итак, исходными данными являются пары чисел (точки)

 

(x_l,y₁), (x₂,y₂), …, (x_n,y_n).       (*)

 

где n – число испытаний. Наряду с анализом величин X и Y по отдельности представляет интерес исследование возможной зависимости между ними. Являются ли величины X и Y независимыми? Если же между ними имеется некоторая зависимость, то какова она?

 

ЧТО ТАКОЕ КОРРЕЛЯЦИЯ?

 

КОРРЕЛЯЦИЯ (лат. correlatio - соотношение) - понятие, указывающее на статистическую связь, существующую между изучаемыми явлениями.

 

КАКОЕ ИССЛЕДОВАНИЕ НАЗЫВАЕТСЯ КОРРЕЛЯЦИОННЫМ?

 

Корреляционным называется исследование, проводимое для подтверждения или опровержения гипотезы о статистической связи между несколькими (двумя и более) переменными.  Наиболее распростра­ненной схемой современного эмпирического исследования является кор­реляционное исследование. Теория корреляционного исследования основана на представлениях о мерах корреляционной связи, ее основы были заложены К. Пирсоном в работах по математической статистике. 

 

ВИДЫ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ.

 

«Корреляция» в прямом переводе означает «соотношение», и в широком смысле слова корреляция означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. При измерении тесноты связи говорят о корреляции в узком смысле слова. Если изменение од­ной переменной сопровождается изменением другой, то можно говорить о корреля­ции этих переменных. Наличие корреляции двух переменных ничего не говорит о причинно-следственных зависимостях между ними, но дает возможность выдвинуть такую гипотезу. Отсутствие же корреляции позволяет отвергнуть гипотезу о при­чинно-следственной связи переменных. Корреляционные связи различаются по своему виду.

 

КАКИЕ ВИДЫ КОРРРЕЛЯЦИИ ОТНОСИТЕЛЬНО ТИПА СОЕДИНЕНИЯ ЯВЛЕНИЙ  СУЩЕСТВУЮТ?

 

Относительно типа соединения явления различают:

 

1) непосредственную корреляцию;

 

2) косвенную корреляцию;

 

3) ложную корреляцию.

 

КАКИЕ ВИДЫ КОРРЕЛЯЦИИ ОТНОСИТЕЛЬНО ЧИСЛА ПЕРЕМЕННЫХ СУЩЕСТВУЮТ?

 

Относительно числа переменных различают:

 

1) простую корреляцию;

 

2) множественную корреляцию;

 

3) частную корреляцию.

 

В частности, различают несколько интерпретаций нали­чия корреляционной связи между двумя переменными X и Y:

 

ПРЯМАЯ КОРРЕЛЯЦИОННАЯ СВЯЗЬ. Уровень одной переменной непосредственно соответствует уровню другой.

 

ПРИМЕРЫ. Примером прямой корреляционной связи является закон Хика: скорость переработ­ки информации пропорциональна логарифму от числа альтернатив. Другой пример: корреляция высокой личностной пластичности и склонности к смене социальных установок.

 

 КОРРЕЛЯЦИЯ, ОБУСЛОВЛЕННАЯ 3-Й ПЕРЕМЕННОЙ.

 

Две переменные (X, Y) связаны одна с другой через 3-ю переменную (Z), не измеренную в ходе исследования.

 

Тогда по свойству транзитив­ности имеем:  

 

если R(X,Z) и R(Z,Y),  то R(X,Y).

 

ПРИМЕРЫ. Примером подобной корреляции явля­ется установленный психологами США факт связи уровня интеллекта с уровнем доходов.  Другой пример: скорость опозна­ния изображения при его быстром (тахистоскопическом) предъявлении и словарный запас испытуемых также положительно коррелируют. Скрытой переменной, обу­словливающей эту корреляцию, является общий интеллект.

 

СЛУЧАЙНАЯ КОРРЕЛЯЦИЯ, не обусловленная никакой переменной.

 

КОРРЕЛЯЦИЯ, ОБУСЛОВЛЕННАЯ НЕОДНОРОДНОСТЬЮ ВЫБОРКИ.

 

ПРИМЕР. Представим себе, что выборка, которую мы будем обследовать, состоит из двух однородных групп. Напри­мер, мы хотим выяснить, связана ли принадлежность к определенному полу с уров­нем экстраверсии (экстра­версию можно измерить, например, с помощью опросника Айзенка ETI-1). Если мы взяли две группы испытуемых: мужчи­ны-математики и женщины-журналистки, то неудивительно, если мы получим линейную зависимость между полом и уровнем экстраверсии—интроверсии: в нашем случае боль­шинство мужчин будут интровертами, а большинство женщин — экстравертами.

 

КАКИЕ ВИДЫ КОРРЕЛЯЦИИ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА КОРРЕЛЯЦИИ   СУЩЕСТВУЮТ?

 

Относительно характера корреляции различают:

 

1) положительную корреляцию;

 

2)  отрицательную корреляцию;

 

Если повышение уровня од­ной переменной сопровождается повышением уровня другой, то речь идет о поло­жительной корреляции. Например, возрастание громкости звука сопровождается ощущением по­вышения его тона.

 

Если рост уровня одной переменной сопровождается снижением уровня другой, то мы имеем дело с отрицательной корреляцией.  Например, чем боязливей особь, тем меньше у нее шансов занять доминирующее положение в группе.

 

Нулевой называется корреляция при отсутствии связи переменных.

 

 

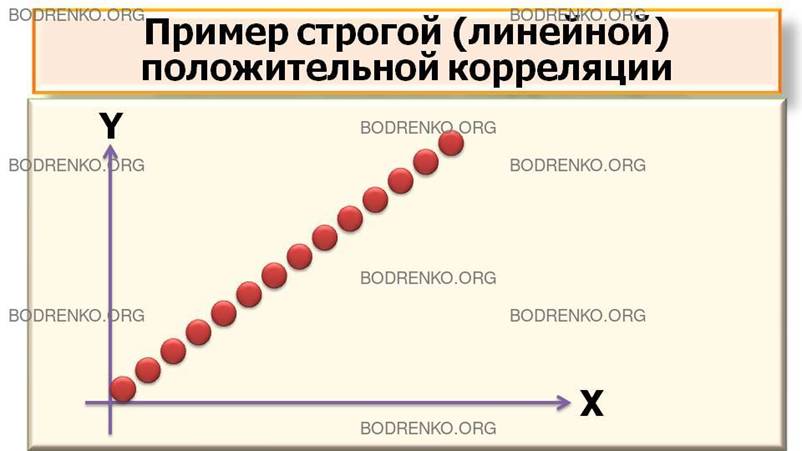
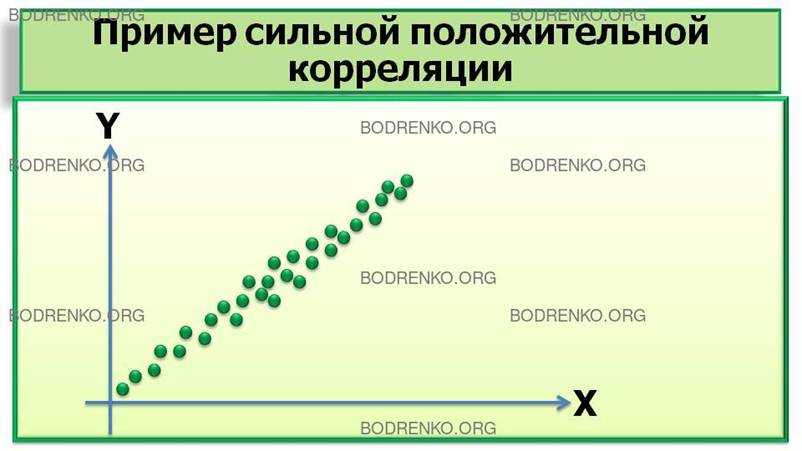
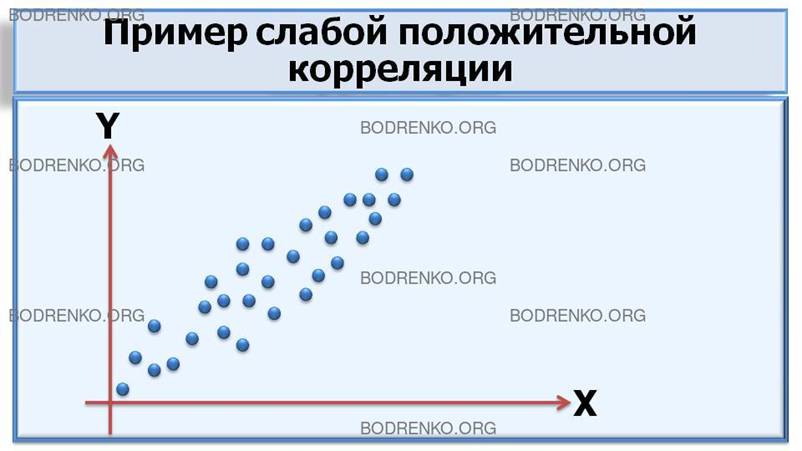
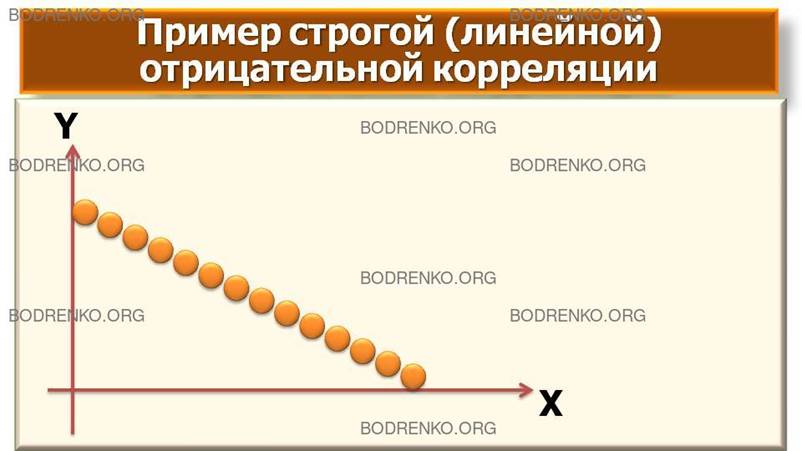
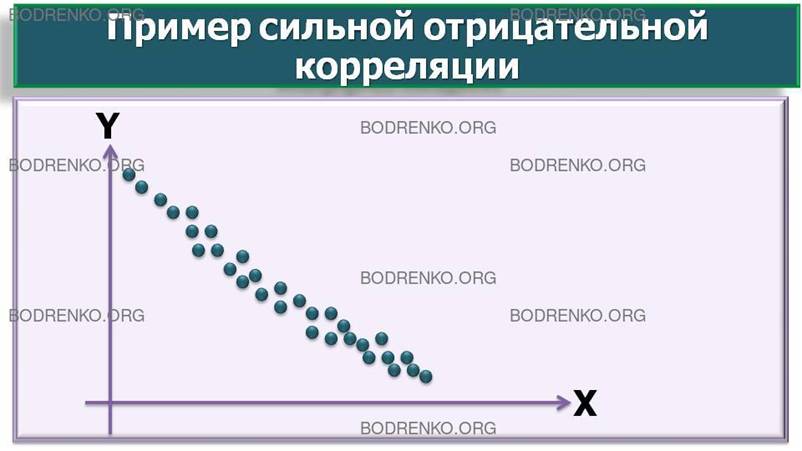
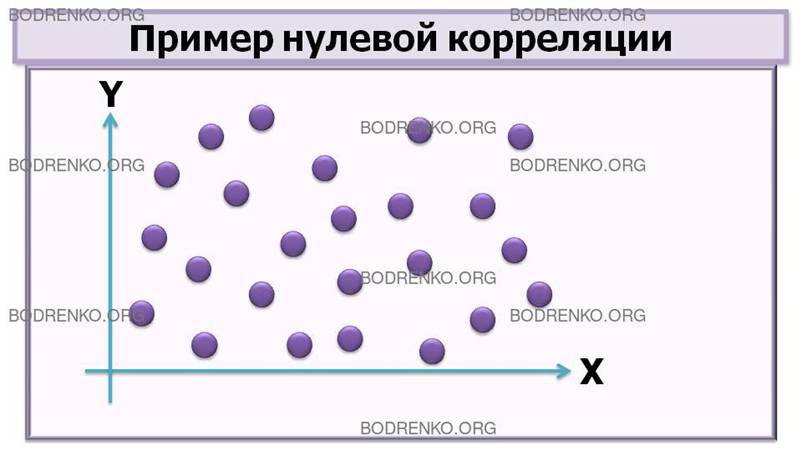
Рисунок 1. Графическая интерпретация корреляционных связей между случайными величинами X и Y (*).

 

 

КАКИЕ ВИДЫ КОРРЕЛЯЦИИ ОТНОСИТЕЛЬНО ФОРМЫ СВЯЗИ  СУЩЕСТВУЮТ?

 

Относительно формы связи выделяют:

 

1) линейную корреляцию;

 

2) нелинейную корреляцию.

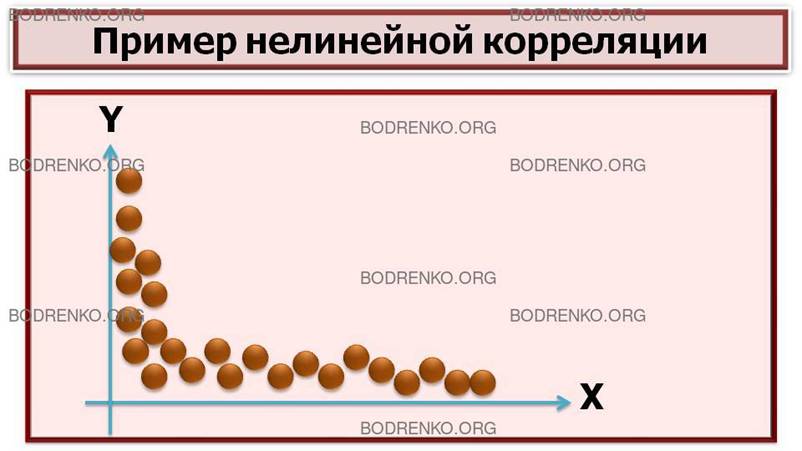
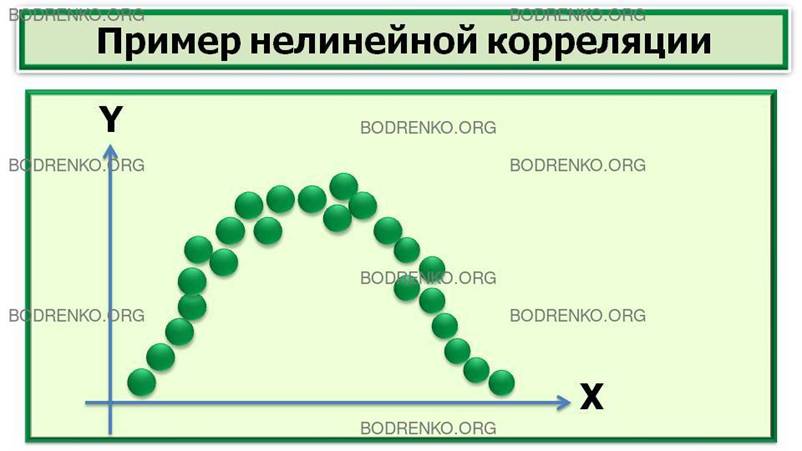
ЗАМЕЧАНИЕ. Математическую теорию линейных корреляций разработал К. Пирсон. Хотя в реальной экономике мало примеров строго линейных связей (положитель­ных или отрицательных). Большинство связей – нелинейные. Классический при­мер нелинейной корреляционной зависимости — закон Йеркса—Додсона: возрастание мотивации первоначально повышает эффективность научения, а затем наступает снижение продуктивности (эффект «перемотивации»). Другим примером является связь меж­ду уровнем мотивации достижений и выбором задач различной трудности. Лица, мо­тивированные надеждой на успех, предпочитают задания среднего диапазона труд­ности — частота выборов на шкале трудности описывается колоколообразной кривой.

 

ЧТО ТАКОЕ КОРРЕЛЯЦИОННЫЙ АНАЛИЗ?

 

Любое причинно-следственное влияние может выражаться либо функциональной, либо корреляционной связью. Но не каждая функция или корреляция соответствует причинно-следственной зависимости между явлениями. Поэтому требуется обязательное исследование причинно-следственных связей. Исследование корреляционных связей мы называем корреляционным анализом, а исследование односторонних стохастических зависимостей регрессионным анализом. Корреляционный и регрессионный анализ имеют свои задачи.

 

В ЧЕМ СОСТОЯТ ЗАДАЧИ КОРРЕЛЯЦИОННОГО АНАЛИЗА?

 

1. Измерение степени связности (тесноты, силы) двух и более явлений. Здесь речь идет в основном о подтверждении уже известных связей.

 

2. Отбор факторов, оказывающих наиболее существенное влияние на результативный признак на основе измерения тесноты связи между явлениями.

 

3. Обнаружение неизвестных причинных связей. Корреляция непосредственно не выявляет причинно-следственных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждений об их наличии. Причинный характер связей выясняется с помощью логически-профессиональных рассуждений, раскрывающих механизм связей.

 

МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ИНТЕРПРЕТАЦИЯ ДАННЫХ КОРРЕЛЯЦИОННОГО ИССЛЕДОВАНИЯ.

 

Дан­ные структурного корреляционного исследования представляют собой одну или не­сколько матриц. Первичная обработка заключается в под­счете коэффициентов статистической связи между двумя и более переменными. Выбор меры связи определяется шкалой, с помощью которой произведены изме­рения.

 

СЛУЧАЙ 1.Стохастическая связь между качественными переменными номинативной шкалы называется сопряженностью. При исследовании степени тесноты связи между качественными номинативными (но не дихотомическими) признаками используются коэффициенты сопряженности Пирсона.   

 

СЛУЧАЙ 2. Если измерения произведены по дихотомической шкале, то для подсчета тес­ноты связи признаков применяется «коэффициент ассоциации» - коэффициент контингенции Пирсона (φ-коэффициент).

 

Коэффициент контингенции Пирсона (φ-коэффициент).

Дихотомическая корреляция используется при исследовании степени тесноты между переменными X и Y, каждый из которых представлен в виде двух альтернатив («1» – «0»). Расчетная таблица φ-коэффициента Пирсона (тетрахорическая таблица) состоит из четырех ячеек (рисунок 2):

 

ПЕРЕМЕННЫЕ		X
		«1»	«0»
Y	«1»	a	b
	«0»	c	d

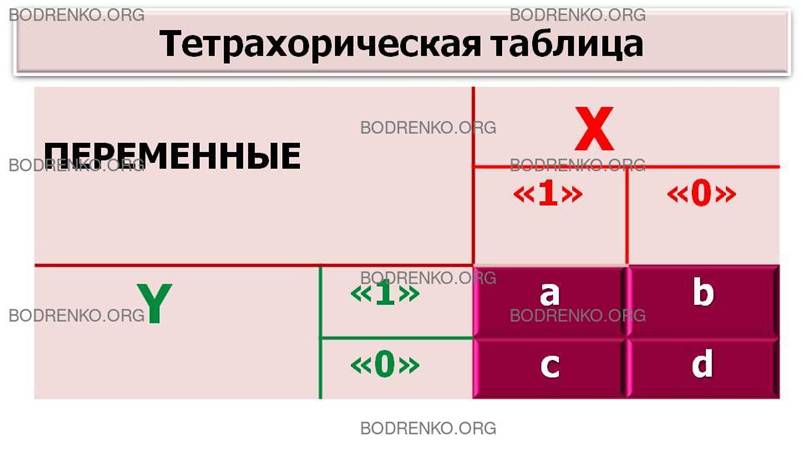
Рисунок 2. Тетрахорическая таблица.

 

Частоты a, b, c, d называются тетрахорическими показателями, их сумма равна объему выборки: N = a + b + c + d.

 

Каждая из клеток тетрахорической таблицы соответствует частоте выбора определенной альтернативы того и другого признака.  Например, частота b определяет количество случаев, в которых зарегистрировано «0» по переменной X и «1» по переменной Y.

 

φ-коэффициент Пирсона определяется по формуле

 

 

Проверка гипотезы о значимости связи между исследуемыми переменными осуществляется с помощью критерия χ² .

 

Для этого эмпирическое значение

 

χ² = φ ² · N,  где N – объем выборки, 

 

сравнивается с критическим χ_α² (1) для числа степеней свободы df = 1:

 

χ_α1 ² = 3,841 (для α₁ = 0,05); χ_α2² = 6,635  (для α₂ = 0,01).

 

Если выполняется условие χ_э² ≤ χ² (для α = 0,05)  (1), то нулевая гипотеза H₀: φ = 0, не отвергается.

 

При χ_э² > χ² (для α = 0,01)  нулевая гипотеза H₀:  φ = 0, отвергается, и связь считается значимой.

ПРИМЕР.  Изучается общественное мнение по очень важному поводу. Распределение ответов респондентов, мужчин и женщин, приведено в таблице (рисунок 3). Требуется определить наличие связи между полом и определенным мнением.

 

Переменные		X - «Мнение»
		«положительное»	«отрицательное»
Y – «Пол»	мужчины	59	41
	женщины	36	64

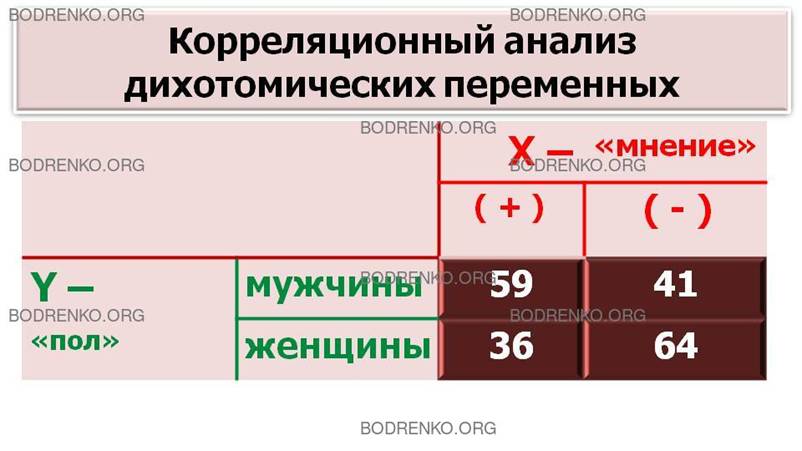
Рисунок 3. Тетрахорическая таблица.

РЕШЕНИЕ.  При корреляционном анализе дихотомических переменных используем коэффициент контингенции Пирсона (φ-коэффициент).

 

Нулевой гипотезой H₀ является предположение об отсутствии связи между рассматриваемыми переменными.  Для ее проверки определяем значение φ-коэффициента Пирсона и критическое значение «хи-квадрат»:

φ =   – 0, 23

 

N = 200

 

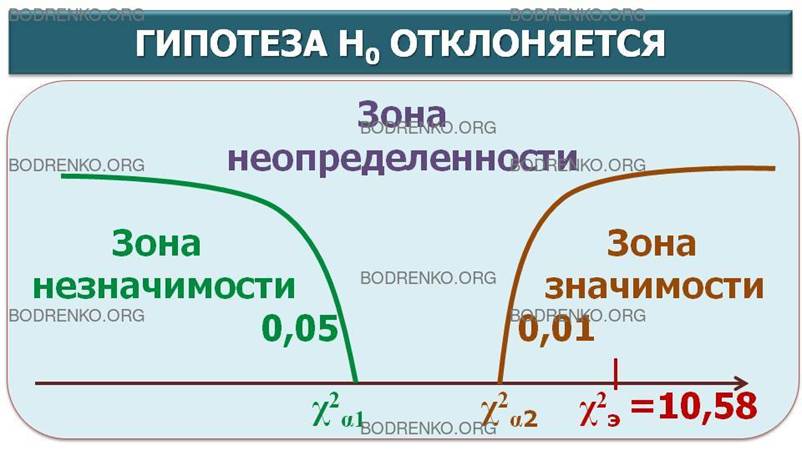
χ ²_э = (-0,23) ² · 200 = 10,580 > 6,635.

Вследствие того, что эмпирическое значение попало в критическую область: χ²_э > χ² (для α = 0,01) , нулевая гипотеза φ = 0 отвергается, связь между полом и определенным мнением можно считать значимой (α < 0,01).

СЛУЧАЙ 3. Данные представлены в порядковой шкале. Мерой связи, которая соответству­ет шкале порядка, является коэффициент ранговой корреляции Кендалла. Коэффициент корреляции «тау» Кендалла имеет те же свойства, что и коэффициент Спирмена (изменяется от –1 до +1, для независимых случайных величин равен нулю), однако он считается более информативным. Он основан на подсчете несов­падений в порядке следования ранжировок Х и Y.  (Например, есть ряд испытуемых: сначала мы выстраиваем этот ряд в порядке убывания массы тела, а затем — в порядке убыва­ния роста). Для каждой пары подсчитывается число совпадений и инверсий: совпа­дение, если их порядок по Х и Y одинаков; инверсия, если порядок различен. Разни­ца числа «совпадений» и числа «инверсий», деленная на N(N–1)/2, (N – число ранжируемых признаков, черт) дает коэффи­циент «тау». Число совпадений обозначим через P, число инверсий – через Q. Эмпирическое значение коэффициента ранговой корреляции «тау» вычисляется по формуле:

 

 

В ЧЕМ СОСТОИТ МЕТОД РАНГОВОЙ КОРРЕЛЯЦИИ СПИРМЕНА?

 

Часто для обработки данных, полученных с помощью шкалы порядка, используют коэффициент r_S ранговой корреляции Спирмена, его рекомендуют применять в том случае, если одно измерение произведено по шкале порядков, а другое — по шкале интер­валов.

 

Метод ранговой корреляции Спирмена является непараметрическим методом, является универсальным и работает с данными,  измеренными в любых шкалах, и прост в применении. Уникальность метода ранговой корреляции состоит в том, что он позволяет сопоставлять не индивидуальные показатели, а индивидуальные иерархии, или профили, что недоступно ни одному из других статистических методов, включая метод линейной корреляции.  Метод ранговой корреляции Спирмена позволяет определить тесноту (силу) и направление корреляционной связи между двумя признаками или двумя профилями (иерархиями) признаков. Для подсчета коэффициента ранговой корреляции Спирмена необходимо иметь два ряда значений, которые могут быть проранжированы.  Вначале показатели ранжируются отдельно по каждому из признаков A, B. Каждая из двух совокупностей располагается в виде вариационного ряда с присвоением каждому члену ряда соответствующего порядкового номера (ранга), выраженного положительным числом. Одинаковым значениям ряда присваивают среднее ранговое число. Сравниваемые признаки можно ранжировать в любом направлении как в сторону ухудшения качества (ранг 1 получает самый большой, быстрый, умный и т. д.), так и наоборот.  Главное, чтобы обе переменные были проранжированы одинаковым способом. Как правило, меньшему значению признака начисляется меньший ранг.

 

ПО КАКОЙ ФОРМУЛЕ ВЫЧИСЛЯЕТСЯ КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ СПИРМЕНА?

 

Коэффициент ранговой корреляции Спирмена находится по формуле

 

 

где d_i – разность рангов для каждой i–пары из N наблюдений.

 

Коэффициент r_s  ранговой корреляции Спирмена  изменяется от –1 до +1.  Для подсчета коэффициента ранговой корреляции Спирмена r_s необходимо определить разности

 

d_i=x_i – y_i

 

между рангами, полученными по обоим признакам.  Затем эти значения  d_i подставляем в формулу (1).  Чем меньше разности между рангами, тем больше будет r_s, тем ближе он будет к (+1). Если корреляция отсутствует, то все ранги будут перемешаны и между ними не будет никакого соответствия. Формула (1) составлена так, что в этом случае коэффициент r_s окажется близким к 0. В случае отрицательной корреляции низким рангам по одному признаку будут соответствовать высокие ранги по другому признаку, и наоборот. Чем больше несовпадение между рангами по двум переменным, тем ближе r_s к (– 1).

Если в вариационных рядах для Xi и Yi встречаются члены ряда с одинаковыми ранговыми числами, то в формулу для коэффициента корреляции Спирмена необходимо внести поправки T_X и T_Y на одинаковые ранги:

 

 

Где T_X  и  T_Y  вычисляются по формулам:

 

 

                                                                                    (3), (4)

В формуле (3) m – количество групп в ранговом ряду X с одинаковыми ранговыми числами; Соответственно, a₁, a₂, …, a_m  (a_j > 1) – это объемы  каждой группы с одинаковыми рангами  в первом ранговом ряду X.

 

В формуле (4) p – количество групп в ранговом ряду Y с одинаковыми ранговыми числами. Соответственно,  b₁, b₂, …, b_p (b_k > 1) – это объемы  каждой группы  с одинаковыми рангами во втором ранговом ряду Y.

 

СЛУЧАЙ 4. Данные получены по шкале интервалов, или отношений. В этом случае применяется стандартный коэффициент линейной корреляции Пирсона или коэффициент ранговой корреляции Спирмена.

 

В КАКИХ СЛУЧАЯХ ИСПОЛЬЗУЕТСЯ КОЭФФИЦИЕНТ ЛИНЕЙНОЙ КОРРЕЛЯЦИИ ПИРСОНА?

 

Коэффициент линейной корреляции Пирсона используется для оценки тесноты (силы) связи между двумя переменными в случаях, если: 1) рассматриваемая связь линейная; 2) обе переменные измерены в сильных шкалах (шкале отношений или интервальной шкале).

 

Если зависимость близка к линейной, т. е. точки заметным образом группируются вокруг некоторой прямой, то в таких случаях говорят о линейной корреляции величин X и Y. В этом случае определение степени  коррелированности случайных величин основано на вычислении коэффициента корреляции r_xy. Если понятно, о каких случайных величинах идет речь, будем вместо r_xy писать просто r.

 

Коэффициент корреляции обладает следующим свойством:

 

-1≤r≤+1.

 

При этом,  чем ближе r к нулю, тем слабее корреляция. И наоборот, чем ближе коэффициент корреляции r к (+1) или (-1), тем сильнее корреляция, т. е. зависимость между X и Y близка к линейной. Если значение r в точности равно (+1) или (- 1), то точки (*) лежат на одной прямой.

 

Подчеркнем, что коэффициент корреляции r отражает степень линейной зависимости между величинами. При наличии ярко выраженной зависимости другого вида (например, квадратичной) он может быть близок к нулю.

 

Приведем формулы для вычисления r_xy :

 

 

СЛУЧАЙ 5. Бисериальная  корреляция является методом корреляционного анализа между двумя переменными, одна из которых измерена в дихотомической шкале. В том случае, если одна переменная является дихотомиче­ской, а другая — интервальной, то используется так называемый точечный бисериальный коэф­фициент корреляции Пирсона. Если первая переменная измерена в дихотомической шкале, вторая переменная измерена в порядковой шкале, то решение задач данного класса осуществляется с помощью рангово-бисериального коэффициента корреляции.

СЛУЧАЙ 6. Если исследователь полагает, что связи между переменными нелиней­ны, он вычисляет корреляционное отношение, характеризующее величину нелиней­ной статистической зависимости двух переменных.

 

СЛУЧАЙ 7. Коэффициент конкордации (согласованности) Кендалла используется в случае, когда совокупность объектов характеризуется несколькими последовательностями рангов, исследователю необходимо установить статистическую связь между этими последовательностями. Такие задачи возникают, например, при анализе экспертных оценок: несколько экспертов ранжируют одних  и тех же испытуемых по определенному качеству, а исследователю для проведения углубленного анализа ситуации и принятия обоснованного решения требуется определить степень согласованности мнений группы экспертов.

 

Значения коэффициента конкордации W, в отличие от коэффициента корреляции, заключены в интервале 0 ≤ W ≤ 1 . Коэффициент конкордации равен единице при полном совпадении всех ранговых последовательностей. Если мнения экспертов (ранговые последовательности) полностью противоположны, коэффициент конкордации равен нулю (коэффициент корреляции в этом случае будет равен –1).

 

ЧЕМ ЗАВЕРШАЕТСЯ КОРРЕЛЯЦИОННОЕ ИССЛЕДОВАНИЕ?

 

Корреляционное исследование завершается выводом о статистической значимо­сти установленных (или неустановленных) зависимостей между переменными. Од­нако исследователи не ограничиваются такой констатацией. Одна из главных задач, которые возникают, выяснить, не обусловлены ли связи меж­ду отдельными параметрами скрытыми факторами? Для этой цели применяется, например, аппарат редукции числа переменных: методы многомер­ного анализа данных.

 

РЕГРЕССИЯ.

 

Односторонняя вероятностная зависимость между случайными  величинами есть регрессия. Она устанавливает соответствие между этими величинами. Односторонняя стохастическая зависимость выражается с помощью функции, которая называется регрессией.

 

Предположим, что зависимость между случайными величинами X и Y близка к линейной. В этом случае коэффициент корреляции r близок к (+1)  или (-1).

 

Тогда естественно ставить вопрос об отыскании функции

 

 y=ax+b,  (***)

 

которая наилучшим образом выражает зависимость Y от X. Для нахождения такой функции пользуются методом наименьших квадратов.

 

Итак, пусть даны n пар чисел (иначе говоря, n точек):

 

(x_l,y₁), (x₂,y₂), …, (x_n,y_n).       (*)

 

где n – число испытаний.

Требуется найти такую прямую, чтобы сумма квадратов «отклонений» этих точек от прямой (***) была как можно меньше. Это означает, что выражение (Δ)

 

должно быть минимальным (на рис. 5 отклонения изображены в виде вертикальных отрезков).

 

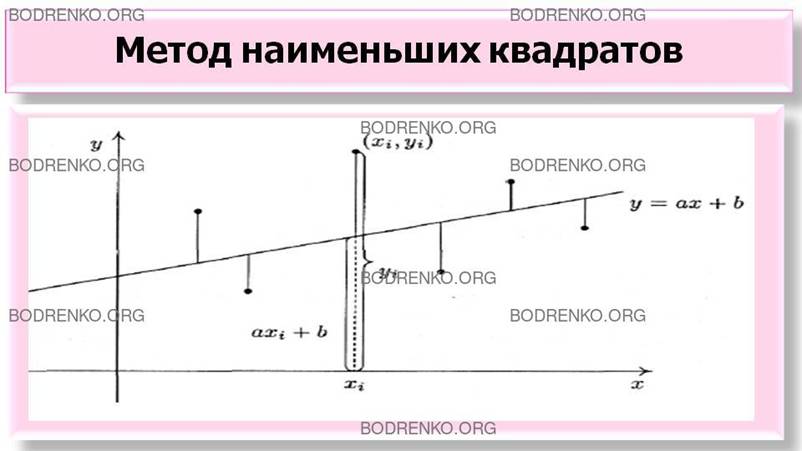
Рисунок 5. Метод наименьших квадратов.

 

Выражение (Δ) является функцией двух переменных а и b (поскольку результаты наблюдений заданы). Можно показать, что выражение (Δ) принимает минимальное значение, если величины а и b связаны соотношениями:

 

Эта система имеет единственное решение:

 

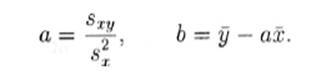
Найдя значения неизвестных параметров a и b, мы найдем тем самым прямую (***), наилучшим образом выражающую статистическую связь между величинами X и Y.

 

Полученная прямая (***) называется прямой регрессии Y на X.

 

ВИДЫ РЕГРЕССИЙ.

 

КАКИЕ ВИДЫ РЕГРЕССИЙ ОТНОСИТЕЛЬНО ЧИСЛА ПЕРЕМЕННЫХ СУЩЕСТВУЮТ?

 

Виды регрессии относительно числа переменных следующие.

 

1) простая регрессия — регрессия между двумя переменными;

 

2) множественная регрессия — регрессия между зависимой переменной y и несколькими объясняющими переменными х₁, x₂, ..., x_m.

 

ПРИМЕР. Например, множественная линейная регрессия имеет следующий вид:

 

y=a₀+a₁∙x₁+a₂∙x₂+ …+a_m∙x_m ,    (**)

 

где y – функция регрессии;

 

x₁, x₂, …, x_m – независимые переменные;

 

a1, a₂, ..., a_m – коэффициенты регрессии;

 

a0 – свободный член уравнения регрессии;

 

m – число факторов, включаемых в модель.

КАКИЕ ВИДЫ РЕГРЕССИЙ ОТНОСИТЕЛЬНО ФОРМЫ ЗАВИСИМОСТИ  СУЩЕСТВУЮТ?

 

Виды регрессии относительно формы зависимости следующие.

 

1) линейная регрессия, выражаемая линейной функцией;

 

2) нелинейная регрессия, выражаемая нелинейной функцией.

 

КАКИЕ ВИДЫ РЕГРЕССИЙ В ЗАВИСИМОСТИ ОТ ХАРАКТЕРА РЕГРЕССИИ  СУЩЕСТВУЮТ?

 

В зависимости от характера регрессии различаются следующие ее виды.

 

1) положительная регрессия: она имеет место, если с увеличением (уменьшением) объясняющей переменной значения зависимой переменной также соответственно увеличиваются (уменьшаются);

 

2) отрицательная регрессия: в этом случае с увеличением (или уменьшением) объясняющей переменной зависимая переменная уменьшается (или увеличивается).

 

КАКИЕ ВИДЫ РЕГРЕССИЙ В ЗАВИСИМОСТИ ОТ ТИПА СОЕДИНЕНИЯ ЯВЛЕНИЙ  СУЩЕСТВУЮТ?

 

Относительно типа соединения явлений различаются следующие виды регрессий.

 

1) непосредственная регрессия: в этом случае зависимая и объясняющая переменные связаны непосредственно друг с другом;

 

2) косвенная регрессия: в этом случае объясняющая переменная действует на зависимую через ряд других переменных;

 

3) ложная регрессия: она возникает при формальном подходе к исследуемым явлениям без уяснения того, какие причины обусловливают данную связь.

 

Регрессия тесно связана с корреляцией.

 

В  ЧЕМ ЗАКЛЮЧАЮТСЯ ЗАДАЧИ РЕГРЕССИОННОГО АНАЛИЗА?

 

Если случайные переменные причинно обусловлены и можно в вероятностном смысле высказаться об их связи, то имеется корреляция. Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила связи, а в регрессионном анализе исследуется ее форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.

 

Задачи регрессионного анализа следующие.

 

1. Установление формы зависимости (линейная или нелинейная; положительная или отрицательная и т. д.).

 

2. Определение функции регрессии и установление влияния факторов на зависимую переменную. Важно не только определить форму регрессии, указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую  переменную главных факторов, если бы прочие не изменялись и если бы были исключены случайные элементы. Для этого определяют функцию регрессии в виде математического уравнения того или иного типа.

 

3. Оценка неизвестных значений зависимой переменной, т. е. решение задач экстраполяции и интерполяции. В ходе экстраполяции распространяются тенденции, установленные в прошлом, на будущий период. Экстраполяция широко используется в прогнозировании. В ходе интерполяции определяют недостающие значения, соответствующие моментам времени между известными моментами, т. е. определяют значения зависимой переменной внутри интервала заданных значений факторов.

 

РАЗДЕЛ 3. ЭТАПЫ ПОСТРОЕНИЯ МНОГОФАКТОРНОЙ КОРРЕЛЯЦИОННО-РЕГРЕССИОННОЙ МОДЕЛИ.

 

Разработка многофакторной корреляционно-регрессионной модели и исследование экономических процессов должны выполняться по следующим этапам.

 

ЭТАП 1. Априорное исследование экономической проблемы.

 

ЭТАП 2. Формирование перечня факторов и их логический анализ.

 

ЭТАП 3. Сбор исходных данных и их первичная обработка.

 

ЭТАП 4. Спецификация функции регрессии.

 

ЭТАП 5. Оценка функции регрессии.

 

ЭТАП 6. Отбор главных факторов.

 

ЭТАП 7. Проверка адекватности модели.

 

ЭТАП 8. Экономическая интерпретация.

 

ЭТАП 9. Прогнозирование неизвестных значений зависимой переменной.

 

Рассмотрим подробнее содержание этапов.

 

Этап 1. Априорное исследование экономической проблемы.  

 

В соответствии с целью работы на основе знаний макро- и микроэкономики конкретизируются явления, процессы, зависимость между которыми подлежит оценке. При этом подразумевается, прежде всего, четкое определение экономических явлений, установление объектов и периода исследования. На этом этапе исследования должны быть сформулированы экономически осмысленные и приемлемые гипотезы о зависимости экономических явлений.

 

Этап 2. Формирование перечня факторов и их логический анализ.

 

Для определения наиболее разумного числа переменных в регрессионной модели прежде всего ориентируются на соображения профессионально-теоретического характера. Исходя из физического смысла явления, производят классификацию переменных на зависимую

и объясняющую.

 

Этап 3. Сбор исходных данных и их первичная обработка.

 

При построении модели исходная информация может быть собрана в трех видах:

 

1) динамические (временные) ряды;

 

2) пространственная информация — информация о работе нескольких объектов в одном разрезе времени;

 

3) сменная — табличная форма. Информация о работе нескольких объектов за разные периоды.

 

Объем выборки зависит от числа факторов, включаемых в модель с учетом свободного члена. Для получения статистически значимой модели требуется на один фактор объем выборки, равный 5 ÷ 8 наблюдений.

 

ПРИМЕР. Например, если в модель включаются три фактора, то минимальный объем выборки равен ≈20 наблюдений. Следовательно, если собирать данные в квартальном разрезе, то надо их собирать за 5 лет (5=20/4).

 

Этап 4. Спецификация функции регрессии.

 

На данном этапе исследования дается конкретная формулировка гипотезы о форме связи (линейная или нелинейная, простая или множественная и т. д.). Для этого используются различные критерии для проверки состоятельности гипотетического вида зависимости. На этом этапе проверяются предпосылки корреляционно-регрессионного анализа.

 

Этап 5. Оценка функции регрессии.  

 

Здесь определяются числовые значения параметров регрессии и вычисление ряда показателей, характеризующих точность регрессионного анализа.

 

Этап 6. Отбор главных факторов.

 

Выбор факторов - основа для построения многофакторной корреляционно-регрессионной модели. На этапе формирования перечня факторов и их логического анализа собираются все возможные факторы, обычно более 20-30 факторов. Но это неудобно для анализа, и модель, включающая 20—30 факторов, будет неустойчива. Неустойчивость модели находит выражение в том, что в ней изменение некоторых факторов ведет к увеличению Y вместо снижения Y. Мало факторов — тоже плохо. Это может привести к ошибкам при принятии решений в ходе анализа модели. Поэтому необходимо выбирать более рациональный перечень факторов. При этом проводят анализ факторов на мультиколлинеарность.

 

АНАЛИЗ И СПОСОБЫ СНИЖЕНИЯ ВЛИЯНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ НА ЗНАЧИМОСТЬ МОДЕЛИ.

 

ЧТО ТАКОЕ МУЛЬТИКОЛЛИНЕАРНОСТЬ?

 

Мультиколлинеарность – это попарная корреляционная зависимость между факторами.

 

Считается, что мультиколлинеарная зависимость между факторами X_i и  X_j присутствует, если коэффициент парной корреляции r_ij удовлетворяет соотношению:

 

r_ij ≥0,70 ÷ 0,80.

 

В ЧЕМ СОСТОИТ ОТРИЦАТЕЛЬНОЕ ВОЗДЕЙСТВИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ?

 

Отрицательное воздействие мультиколлинеарности состоит в следующем:

 

1) усложняется процедура выбора главных факторов;

 

2) искажается смысл коэффициента множественной корреляции (он предполагает независимость факторов);

 

3) усложняются вычисления при построении самой модели;

 

4) снижается точность оценки параметров регрессии, искажается оценка дисперсии.

 

Следствием снижения точности является ненадежность коэффициентов регрессии и отчасти неприемлемость их использования для интерпретации как меры воздействия соответствующей объясняющей переменной на зависимую переменную. Оценки коэффициента становятся очень чувствительными к выборочным наблюдениям. Небольшое увеличение объема выборки может привести к очень сильным сдвигам в значениях оценок. Кроме того, стандартные ошибки оценок входят в формулы критерия значимости, поэтому применение самих критериев становится также ненадежным. Из сказанного ясно, что исследователь должен пытаться установить стохастическую мультиколлинеарность и по возможности устранить ее. Для измерения мультиколлинеарности можно использовать коэффициент множественной детерминации.

 

КАКОЙ МЕТОД ИСПОЛЬЗУЕТСЯ ДЛЯ УСТРАНЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ?

 

Для устранения мультиколлинеарности используется МЕТОД ИСКЛЮЧЕНИЯ ПЕРЕМЕННЫХ. Этот метод заключается в том, что высоко коррелированные объясняющие переменные (факторы) устраняются из регрессии, и она заново оценивается. Отбор переменных, подлежащих исключению, производится с помощью коэффициентов парной корреляции r_yxj  (где r_yxj   – коэффициент парной корреляции между j-м фактором X_j и зависимой переменной Y).

 

Опыт показывает, что если |r_yxj|≥0,70, то одну из переменных можно исключить, но какую переменную исключить из анализа, решают исходя из управляемости факторов на уровне

предприятия. Обычно в модели оставляют тот фактор, на который можно разработать мероприятие, обеспечивающее улучшение значения этого фактора в планируемом году. Возможна ситуация, когда оба мультиколлинеарных фактора управляемы на уровне предприятия. Решить вопрос об исключении того или иного фактора можно только в соответствии с процедурой отбора главных факторов. Отбор факторов не самостоятельный процесс, он сопровождается построением модели. Принятие решения об исключении факторов производится на основе анализа значений специальных статистических характеристик и с учетом управляемости факторов на уровне предприятия.

 

КАКИЕ ЭТАПЫ ВКЛЮЧАЕТ ПРОЦЕДУРА ОТБОРА ГЛАВНЫХ ФАКТОРОВ?

 

Процедура отбора главных факторов обязательно включает следующие этапы:

 

1. Анализ факторов на мультиколлинеарностъ и ее исключение.

 

Здесь производится анализ значений коэффициентов парной корреляции r_ij между факторами X_i и X_j.

 

2.  Анализ тесноты взаимосвязи факторов (Х) с зависимой переменной (Y).

 

Для анализа тесноты взаимосвязи X и Y используются значения коэффициента парной корреляции между фактором X_i  и функцией Y: r_XiY.

 

Величина r_XiY определяется на ЭВМ и представлена в корреляционной матрице (таблица 4).

 

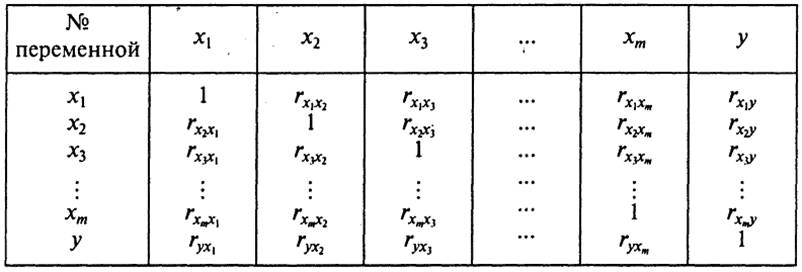
Таблица 4. Корреляционная матрица.

 

Факторы X_i, для которых r_XiY=0, т. е. не связанные с Y, подлежат исключению в первую очередь. Факторы, имеющие наименьшее значение r_XiY, могут быть потенциально исключены из модели. Вопрос об их окончательном исключении решается в ходе анализа других статистических характеристик.

 

3. Анализ коэффициентов  факторов, которые потенциально могут быть исключены.

 

4. Проверка коэффициентов регрессии на статистическую значимость.

 

Проверка может быть произведена двумя способами:

 

- проверка статистической значимости по критерию Стьюдента;

  

- проверка статистической значимости по критерию Фишера.

 

5. Анализ факторов на управляемость.

 

В ходе логического анализа на основе экономических знаний исследователь должен сделать вывод: можно ли разработать организационно-технические мероприятия, направленные на улучшение (изменение) выбранных факторов на уровне предприятия. Если это возможно, то данные факторы управляемы. Неуправляемые факторы на уровне предприятия могут быть исключены из модели.

 

6. Строится новая регрессионная модель без исключенных факторов.

 

Для этой модели определяется коэффициент множественной детерминации Д.

 

7. Исследование целесообразности исключения факторов из модели с помощью коэффициента детерминации.

 

Здесь,  прежде чем вынести решение об исключении переменных из анализа в силу их незначимого влияния на зависимую переменную, производят исследования с помощью коэффициента детерминации.

 

ЭТАП 7. Проверка адекватности модели.

 

Данный этап анализа включает следующие процедуры:

 

- оценку значимости коэффициента детерминации Д. Данная оценка необходима для решения вопроса: оказывают ли выбранные факторы влияние на зависимую переменную? Оценку значимости Д следует проводить, так как может сложиться такая ситуация, когда величина коэффициента детерминации будет целиком обусловлена случайными колебаниями в выборке, на основе которой он вычислен. Это объясняется тем, что величина Д существенно зависит от объема выборки.

 

-  проверку качества подбора теоретического уравнения. Она проводится с использованием средней ошибки аппроксимации.

 

-  вычисление специальных показателей, которые применяются для характеристики воздействия отдельных факторов на результирующий показатель. Это коэффициент эластичности, который показывает, на сколько процентов в среднем изменяется функция с изменением аргумента на 1% при фиксированных значениях других аргументов. Следует отметить, что система факторов, входящая в модель регрессии, - это не простая их сумма, так как система предполагает внутренние связи, взаимодействие составляющих ее элементов.  Действие системы не равно арифметической сумме воздействий составляющих ее элементов. Поэтому необходимо определить показатель системного эффекта факторов.  На основе анализа специальных показателей и значений парной корреляции X с Y делают вывод, какие из главных факторов оказывают наибольшее влияние на Y. После этого переходят к разработке организационно-технических мероприятий, направленных на улучшение значений этих факторов, с целью повышения (снижения) результативного показателя Y.

 

ЭТАП 8. Экономическая интерпретация.

 

На этом этапе результаты регрессионного анализа сравниваются с гипотезами, сформулированными на первом этапе исследования, и оценивается их правдоподобие с экономической точки зрения.

 

ЭТАП 9.  Прогнозирование неизвестных значений зависимой переменной.

 

Полученное уравнение регрессии находит практическое применение в прогностическом анализе. Прогноз получают путем подстановки в регрессию с численно оцененными параметрами значений факторов. Следует подчеркнуть, что прогнозирование результатов по регрессии лучше поддается содержательной интерпретации, чем простая экстраполяция тенденций, так как полнее учитывается природа исследуемого явления. Более подробно вопросы прогнозирования мы рассмотрим на следующей лекции № 5 «Методы и модели прогнозирования временных рядов экономических показателей». 

 

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Бережная Е.В., Бережной В.И. Математические методы моделирования экономических  систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с.: ил.

 

 [2] Колемаев В.А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем.  М.: ЮНИТИ-ДАНА, 2005. - 295 с.

[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. 4-е изд., испр. – М.: Дело, 2003. – 688 с.

 

[4] Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

 

[5] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).