Математическое моделирование экономических систем

 

Лекция 2

 

Тема лекции 2: «Моделирование экономических систем с использованием марковских случайных процессов»

Разделы лекции:

 

1. Случайные величины и законы их распределения. 

2. Основные понятия марковских случайных процессов.

3. Непрерывные марковские цепи.

 

РАЗДЕЛ 1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЗАКОНЫ ИХ РАСПРЕДЕЛЕНИЯ. 

На лекции 1 «Основы вероятностных методов анализа и моделирования экономических систем»  мы рассматривали события, состоящие в появлении того или иного числа. Например, среди трех изъятых из партии деталей может оказаться до трех стандартных. 

 

ЧТО НАЗЫВАЕТСЯ СЛУЧАЙНОЙ ВЕЛИЧИНОЙ?

 

ОПРЕДЕЛЕНИЕ 1. Величину называют случайной, если в результате испытания она примет лишь одно возможное значение, заранее не известное и зависящее от случайных причин.  Каждой случайной величине соответствует множество чисел (множество значений, которые она может принимать).

 

ПРИМЕР 1. Например, число заболевших гриппом в период эпидемии гриппа среди 30 учащихся одного класса школы – это случайная величина, которая может принимать значения от 0 до 30.

 

Далее будем обозначать случайные величины прописными буквами, а их возможные значения – строчными буквами.

 

ПРИМЕР 2. Например, случайная величина Х имеет два возможных значения х₁ и x₂.  

 

Другой пример: случайная величина Y принимает возможные значения, принадлежащие  интервалу (а, b) числовой прямой.

 

ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН.

 

КАКИЕ ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН СУЩЕСТВУЮТ?

 

Различают два вида случайных величин.  

 

ОПРЕДЕЛЕНИЕ 2. Случайная величина, принимающая отдельные возможные значения (числа) с определенными вероятностями, называется  ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНОЙ.

ОПРЕДЕЛЕНИЕ 3. НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНОЙ называется случайная величина, которая может принимать все значения из некоторого числового промежутка.

Как следует из определения 2, для задания дискретной случайной величины нужно задать не только перечень ее возможных значений, но и их вероятности. Иными словами, каждому возможному значению случайной величины соответствует определенное значение вероятности появления этого значения случайной величины.  

 

ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

 

ЧТО ТАКОЕ ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

ОПРЕДЕЛЕНИЕ 4. Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения дискретной случайной величины. 

 

Как и в случае функциональной зависимости, этот закон можно задать таблицей, аналитически (формулой) и графически.

 

В случае табличного задания закона распределения дискретной случайной величины соответствующая таблица состоит из двух строк: в первой строке указаны возможные значения, а во второй строке в соответствующих столбцах под возможными значениями указаны вероятности этих значений.

 

То есть имеем следующую таблицу.

 

Таблица 1.

X	x1	x2	…	xn
P	p1	p2	…	pn

Поскольку в одном испытании случайная величина принимает только одно возможное значение, то события Х=х₁, Х=х₂, ..., Х=х_n образуют полную группу, т.е. сумма их вероятностей равна единице: 

 

p₁+ p₂+ … + p_n = 1.  (1)

 

Если множество возможных значений Х дискретной случайной величины бесконечно, то соответствующий ряд вероятностей сходится и его сумма равна единице:

 

p₁+ p₂+ … + p_n + … = 1.

 

ПРИМЕР 3. В денежной лотерее на 100 билетов разыгрывается один выигрыш в 2000 руб., два выигрыша по 1000 руб. и 10 выигрышей по 100 р. Найти закон распределения случайной величины Х возможного выигрыша на один билет.

РЕШЕНИЕ. Запишем возможные значения случайной величины Х:

 

х₁=2000, х₂=1000, х₃=100, x₄=0.

 

Соответственно их вероятности равны:

 

p₁=0,01; p₂=0,02; р₃=0,1; р₄=1 – (p₁+p₂+p₃) = 1 – 0,13 = 0,87.

 

Таким образом, искомый закон распределения имеет следующий вид.

X	2000	1000	100	0
P	0,01	0,02	0,1	0,87

ПРИМЕР 4. Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.

 
РЕШЕНИЕ. Случайная величина Х – это ЧИСЛО стандартных изделий среди трех отобранных. Поэтому X может принимать 4 возможные значения: 0, 1, 2 и 3.

Вероятность события X=k, то есть того, что среди трех отобранных изделий окажется k стандартных деталей, определяется следующей формулой:

 
Р(Х=k)=(С^k₅∙С^{3 – k} ₃)/C³₈ .   (k=0,1,2,3).

 

В этой формуле

 

число сочетаний С³₈=56 – это число вариантов выбора трех изделий из 8;

 

число сочетаний С^k₅=5!/(k!∙(5 – k)!) – это число вариантов выбора k стандартных изделий из 5 стандартных изделий (здесь k принимает значения 0,1, 2, 3);

 

число сочетаний С^{3 – k} ₃=3!/((3 – k)!∙(k)!) – это число вариантов выбора (3 – k) нестандартных изделий из 3=8 – 5 нестандартных изделий (здесь k принимает значения 0,1, 2, 3);

 

тогда произведение

 

С^k₅∙С^{3 – k} ₃=(5!/(k!∙(5 – k)!))∙(3!/((3 – k)!∙(k)!))

 

дает число вариантов того, что в наудачу выбранных трех изделиях окажется k стандартных (k=0,1,2,3).

Варьируя значения случайной величины X от 0 до 3, найдем соответствующие вероятности:

 

Р(Х=0)=(С⁰₅∙С^{3 –0} ₃)/C³₈ =(1∙1)/56≈0,0179;

 

Р(Х=1)=(С¹₅∙С^{3 –1} ₃)/C³₈ =(5∙3)/56≈0,2679;

 

Р(Х=2)=(С²₅∙С^{3 –2} ₃)/C³₈ =(10∙3)/56≈0,5357;

 

Р(Х=3)=(С³₅∙С^{3 –3} ₃)/C³₈ =(10∙1)/56≈0,1786.

 

Итак, получаем искомое распределение:

 

X	0	1	2	3
P	0,0179	0,2679	0,5357	0,1786

ЧТО ТАКОЕ МНОГОУГОЛЬНИК РАСПРЕДЕЛЕНИЯ  ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

Закон распределения дискретной случайной величины можно изобразить графически, соединив в прямоугольной системе координат XOY точки (х_i; p_i) отрезками прямых. Такая фигура называется многоугольником распределения (рисунок 1).

 

 

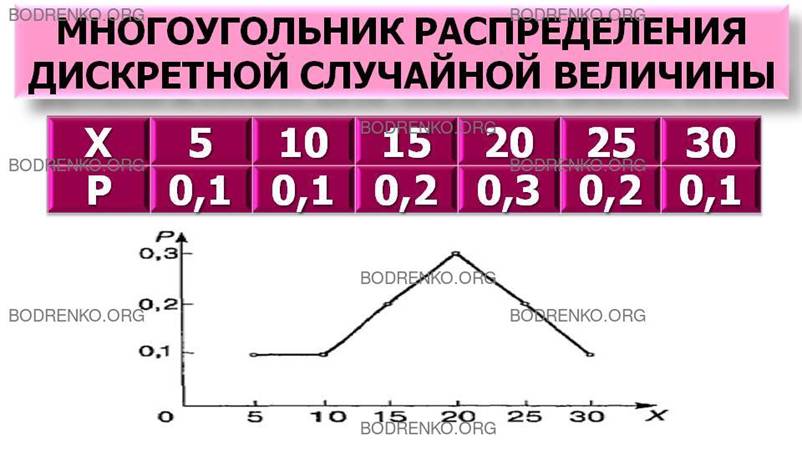
Рисунок 1. Многоугольник распределения дискретной случайной величины.

 

КАК ОПРЕДЕЛЯЕТСЯ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ?

 

БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.

 
Пусть производится n независимых испытаний,  и в каждом из них событие А может либо появиться, либо не появиться. Пусть также вероятность р появления события А в каждом испытании постоянна.

 

В качестве дискретной случайной величины Х рассмотрим число появления события А в этих испытаниях. Очевидно, что

 

х₁=0, x₂=1, x₃=2, ..., x_n+1=n. (2)

Вероятности этих возможных значений случайной величины X даются формулой Бернулли, которую мы ввели на лекции 1 «Основы вероятностных методов анализа и моделирования экономических систем»: 

 

Р_n(k)=C^k_n∙p^k∙q^{n – k}

 

или

 

Рn(k)=(n!/(k!∙(n – k)!))∙p^k∙q^{n – k}.     (3)  

 

где  через q=1 – p обозначена вероятность противоположного события (непоявление события А в одном испытании).

 

Формула (3) представляет собой аналитическую форму записи закона распределения  случайной величины X (числа появления события А в n независимых испытаниях), которое называется биномиальным распределением.  Этот закон получил свое название потому, что правая часть в формуле (3) представляет собой общий член разложения бинома Ньютона, который мы рассмотрели на лекции 1  «Основы вероятностных методов анализа и моделирования экономических систем».

 

КАК ЗАПИСАТЬ В ТАБЛИЧНОМ ВИДЕ БИНОМИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

Таким образом, табличная форма биномиального закона с учетом формулы (3) имеет вид
Р_n(k)=C^k_n∙p^k∙q^{n – k}

 

X	0	1	…	k	…	n
P	qn	n∙p∙qn –1		Ckn∙pk∙qn – k		pn

Можно показать, что сумма всех вероятностей второй строки этой таблицы равна единице, т.е.

n

∑ C^k_n∙p^k∙q^{n – k}  = qⁿ +n∙p∙q^{n –1}  + … + C^k_n∙p^k∙q^{n – k} + … + pⁿ = 1 .

k=0

ПРИМЕР 5. Банк выдает 5 кредитов. Вероятность невозврата кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувшиих кредит по окончании срока кредитования.  

 

РЕШЕНИЕ. Примем за событие А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу каждого из 5 кредитов можно считать за каждое из 5 независимых испытаний.  Вероятность невозврата k кредитов из 5 описывается биномиальным распределением (3),  где р =0,2, q=0,8,  k  принимает значения от нуля до 5.

 

Искомая таблица закона распределения составляется, согласно (3) при n=5,  и имеет следующий вид.

 

X	0	1	2	3	4	5
P	(0,8)5	5∙0,2∙(0,8)4	10∙(0,2)2∙(0,8)3	10∙(0,2)3∙(0,8)2	5∙(0,2)4∙0,8	(0,2)5

 

 

Или после необходимых вычислений окончательно получим:

 

X	0	1	2	3	4	5
P	0,32768	0,4096	0,2048	0,0512	0,0064	0,00032

РАСПРЕДЕЛЕНИЕ ПУАССОНА.

Пусть в каждом из n произвольных испытаний вероятность появления события А равна р. Как мы знаем, для определения вероятности k появлений события А используется формула Бернулли (3); при больших значениях n пользуются асимптотической формулой Лапласа. Однако эта формула плохо подходит для случая, когда р мало.

Для случая малых значений р и больших значений n используется асимптотическая формула Пуассона.  Эта формула выведена при важном допущении, что произведение n∙p  является постоянной величиной, те. n∙р=λ=const. Тогда вероятность того, что событие А наступит ровно k раз дается формулой, которая представляет собой закон распределения Пуассона вероятностей массовых и редких (т.е. маловероятных) событий.

Р_n(k)=λ^k∙exp{- λ}/k!  .  (4) 

ПРИМЕР 6. На базу отправлено 10000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0,0003. Найти вероятность того, что на базу прибудут 4 поврежденные изделия. 

 

РЕШЕНИЕ. По условию задачи n = 10000, р=0,0003,  k=4.

 

Находим  произведение  n∙p=10000∙0,0003=3=λ.

Затем по формуле (4)  найдем и искомую вероятность:  

Р_n(k)=3⁴∙exp{- 3}/4! =81∙exp{-3}/24≈0,168.  

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ  ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

 

Установленный закон распределения полностью характеризует случайную величину. Однако часто используются числовые характеристики случайной величины, которые дают некоторое осредненное описание случайной величины, получаемое на базе закона ее распределения.

 

КАК ОПРЕДЕЛЯЕТСЯ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ  ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

Пусть случайная величина Х может принимать значения x₁, x₂, …, x_n  с вероятностями соответственно p₁, p₂, …, p_n.

ОПРЕДЕЛЕНИЕ 1. Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности:

М(Х) =x₁∙р₁+x₂∙р₂+ … + x_n∙p_n .   (5) 

Из этого определения следует, что математическое ожидание есть некоторая постоянная (неслучайная) величина. Вероятностный же смысл математического ожидания состоит в том, что оно приближенно равно (в особенности для большого числа испытаний) среднему арифметическому значению случайной величины. Это хорошо видно в случае, когда вероятности всех возможных значений дискретной случайной величины равны:

р_i=р=1/n, i=1, 2, …, n.

Тогда из формулы (5) получаем  

М(Х) = (х₁ + x₂ + … + x_n)/n.   (6)  

ПРИМЕР 7. Найти математическое ожидание количества очков, выпадающих при бросании игральной кости.  

РЕШЕНИЕ. Выпадение каждой грани кубика от одного очка до шести имеет одинаковую вероятность р=1/6. Следовательно, по формуле (6) получаем искомое математическое ожидание:

М(Х) =(1+2+3+4+5+6)/6=3,5.  

ПРИМЕР 5 (ПРОДОЛЖЕНИЕ). Найти математическое ожидание числа невозврата кредитов по данным примера 5.  

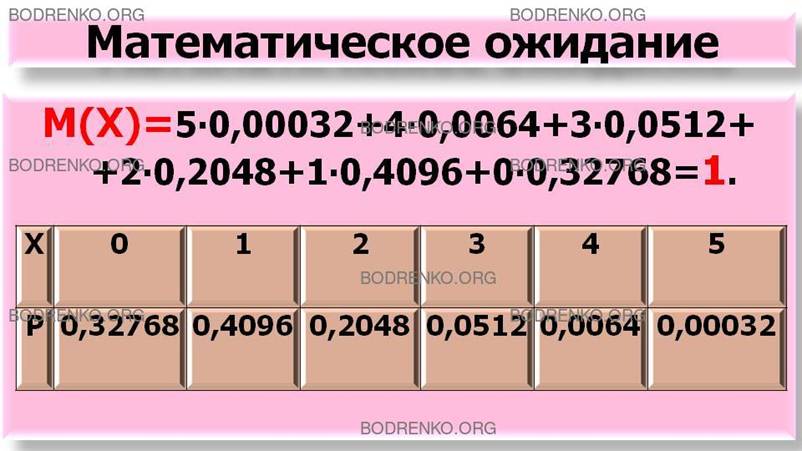
РЕШЕНИЕ. Воспользуемся итоговой таблицей распределения дискретной случайной величины, полученной в этом примере, и формулой (6). Мы имеем:

М(Х) =5∙0,00032+4∙0,0064+3∙0,0512+ 2∙0,2048 + 1∙0,4096 + 0∙0,32768 = 1.  

СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ.

Математическое ожидание обладает рядом свойств, которые мы укажем  ниже.

СВОЙСТВО 1. Математическое ожидание постоянной величины С равно этой постоянной:

М(С)=С.

СВОЙСТВО 2. Постоянный множитель можно выносить за знак математического ожидания:

М(С∙Х) = С∙М(Х).  

СВОЙСТВО 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:

М(Х₁+Х₂ + … + Х_m)= М(Х₁)+М(Х₂) + … + М(Х_m).  

СВОЙСТВО 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:  

М(Х₁∙Х₂ ∙ … ∙Х_m)=М(Х₁)∙М(Х₂)∙ … ∙М(Х_m).  

ПРИМЕР 8. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в некотором автосалоне составляют в среднем 100 тыс. руб., а число продаж Х автомашин в течение дня подчиняется следующему закону распределения:

 

X	0	1	2	3	4	5	6	7	8	9
P	0,25	0,2	0,1	0,1	0,1	0,1	0,05	0,05	0,025	0,025

Найти математическое ожидание ежедневной прибыли при цене на машину 1,5 млн. руб.

РЕШЕНИЕ. Ежедневная прибыль подсчитывается по формуле:

П=(1,5∙Х – 0,1) млн. руб.  

Искомая характеристика М(П) находится с использованием указанных выше свойств математического ожидания (в млн. руб.):

 М(П)=М(1,5∙Х – 0,1)=1,5∙М(Х) – 0,1=1,5∙ 2,675 – 0,1=3,9125 (млн. руб.).  

Если в n независимых испытаниях вероятность появления p в каждом из них события А постоянна, то ответ на вопрос о среднем числе появления события А дает следующая теорема.

ТЕОРЕМА 1. Математическое ожидание М(Х) числа появлений события А в n независимых испытаниях равно произведению числа испытаний n на вероятность появления p события A  в каждом  испытании:

М(Х) = n∙p .  (7)  

ПРИМЕР 9. Найти математическое ожидание числа выигрышных лотерейных билетов, если вероятность выигрыша по одному билету равна 0,015, причем куплено 200 билетов.

 
РЕШЕНИЕ. Поскольку приобретение каждого лотерейного билета является независимым испытанием относительно появления события А (выпадения выигрыша), то здесь применимы теорема 1 и формула (7). В нашем случае n=200, р=0,015, откуда мы получаем

М(200) = 200∙0,015 =3.  

ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

Как мы уже отметили, математическое ожидание является средней характеристикой случайной величины. Однако оно не характеризует случайную величину достаточно полно, и по этой причине рассматриваются и другие числовые характеристики. Пусть Х — случайная величина, а М(Х) — ее математическое ожидание.  

 

ЧТО ТАКОЕ ОТКЛОНЕНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

ОПРЕДЕЛЕНИЕ 2. Разность между случайной величиной X и ее математическим ожиданием M(X) называется отклонением.

 
Пусть закон распределения случайной величины Х дается таблицей 1, тогда отклонение (Х – М(Х)) имеет следующий закон распределения.

 

 

X – M(X)	x1 – M(X)	x2 – M(X)	…	xn – M(X)
P	p1	p2	…	pn

 

ЧЕМУ РАВНО МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ОТКЛОНЕНИЯ?

Отклонение имеет важное свойство, которое устанавливается непосредственно из свойств математического ожидания:

М(Х – М(Х))=0, (9)

т.е. математическое ожидание отклонения равно нулю.  

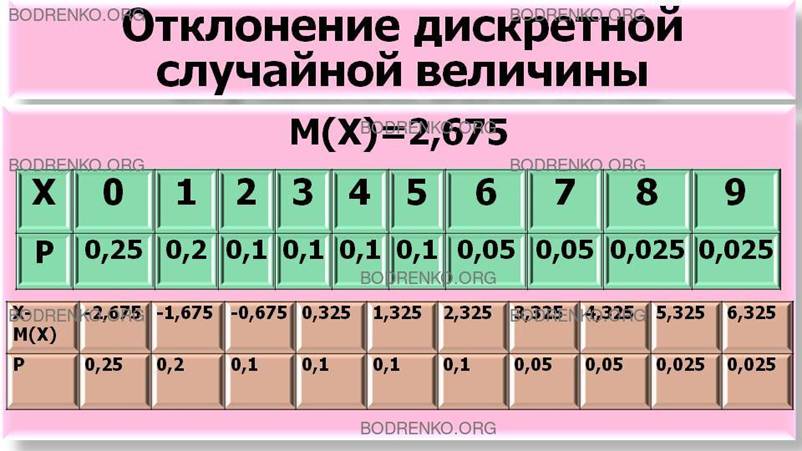
ПРИМЕР 8 (ПРОДОЛЖЕНИЕ). По данным примера 8 найти закон распределения отклонения числа проданных за день автомашин.

РЕШЕНИЕ. Как было подсчитано в примере 8, М(Х)=2,675. Тогда, согласно (18.8), искомый закон определяется следующей таблицей:

 

X-M(X)	-2,675	-1,675	-0,675	0,325	1,325	2,325	3,325	4,325	5,325	6,325
P	0,25	0,2	0,1	0,1	0,1	0,1	0,05	0,05	0,025	0,025

ЧТО ТАКОЕ ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

На практике важной характеристикой является рассеяние возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения, согласно (9), равно нулю.

 

Так как при непосредственном вычислении математического ожидания отклонения в общем случае суммируются отрицательные и положительные отклонения, умноженные на соответствующие вероятности  (см.: пример 8), то целесообразно ввести в рассмотрение абсолютные значения отклонений или их квадраты.

ОПРЕДЕЛЕНИЕ 3. Математическое ожидание квадрата отклонения называется дисперсией (или рассеянием) случайной величины X:  

 

D(Х)=М[Х – М(Х)]². (10)  

Пусть дискретная случайная величина X задана законом распределения (таблица 1), тогда квадрат отклонения этой случайной величины имеет следующий закон распределения:

[X – M(X)]2	[x1 – M(X)]2	[x2 – M(X)]2	…	[xn – M(X)]2
P	p1	p2	…	pn

 

Отсюда, согласно формуле (10), получаем формулу для вычисления дисперсии в развернутом виде:

 

D(Х) =p₁∙[x₁ – M(Х)]² + p₂∙[x₂ – M(Х)]² + … + p_n∙[x_n – M(Х)]² .

При вычислении дисперсии часто бывает удобно воспользоваться формулой, которая непосредственно выводится из формулы (10):

 

D(Х)=М(Х²) — [М(Х)]². (11)

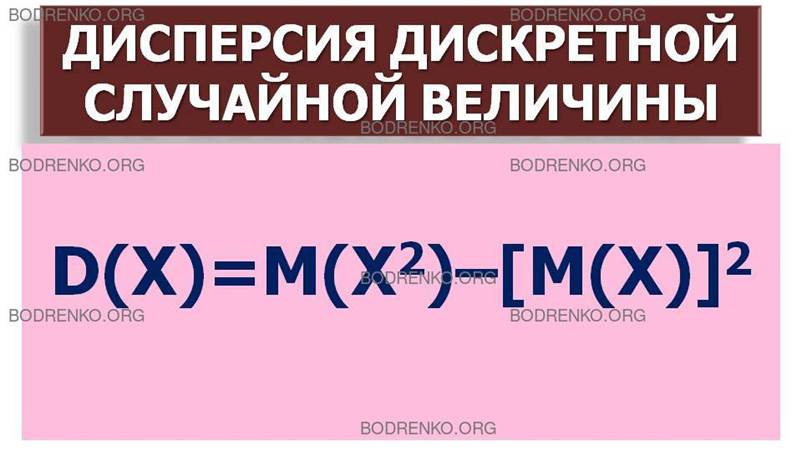
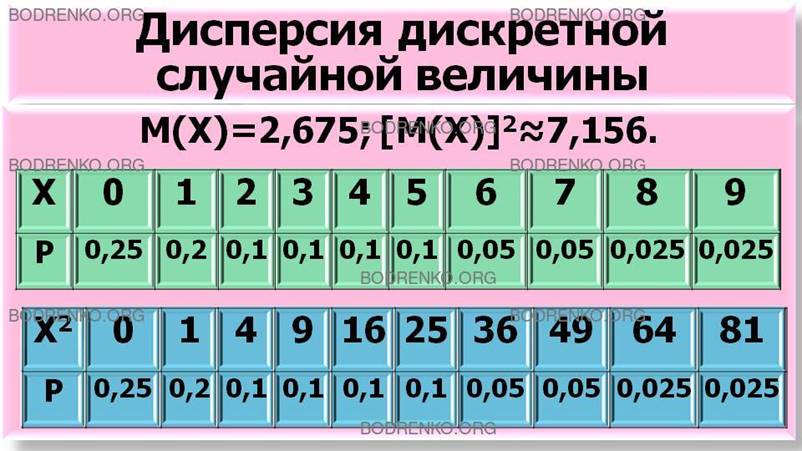
ПРИМЕР 8 (ПРОДОЛЖЕНИЕ). Найти дисперсию ежедневной продажи числа автомашин по данным примера 8.

 

РЕШЕНИЕ. Закон распределения случайной величины Х² имеет вид

X2	0	1	4	9	16	25	36	49	64	81
P	0,25	0,2	0,1	0,1	0,1	0,1	0,05	0,05	0,025	0,025

 

Математическое ожидание М(Х²) подсчитывается из этой таблицы:  

 

М(Х²) =0∙0,25+1∙0,2+4∙0,1+9∙0,1+16∙0,1+25∙0,1+ 36∙0,05 + 49∙0,05 +64∙0,025 +81∙0,025 =13,475.  

 

Математическое ожидание М(Х) =2,675, тогда [М(Х)]² ≈7,156.

Следовательно, согласно формуле (11), получаем искомую величину дисперсии:  

 

D(Х)=М(Х²) – [М(Х)]²= 13,475 – 7,156= 6,319.  

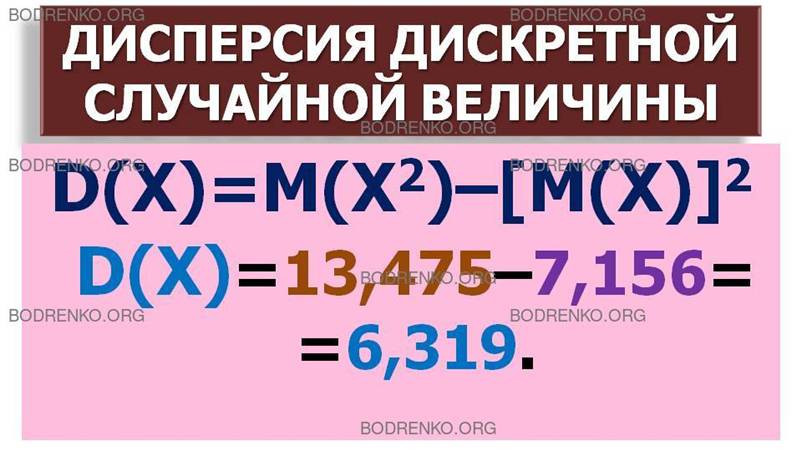
СВОЙСТВА ДИСПЕРСИИ.

 

Приведем здесь основные свойства дисперсии.  

 

СВОЙСТВО 1. Дисперсия постоянной величины С равна нулю:

D(С)=0.

СВОЙСТВО 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

 

D(С∙Х)=С²∙D(Х). (12)

 

СВОЙСТВО 3. Дисперсия алгебраической суммы независимых случайных величин равна сумме их дисперсий:  

 

D(Х₁+Х₂+… +Х_m)=D(Х₁)+D(Х₂) + … + D(Х_m). (13)

Перечисленные свойства дисперсии используются при вычислениях, когда мы имеем дело с несколькими случайными величинами.

 

Из свойств 1 и 3 следует важный вывод:

 

D(Х+С)=D(Х), где С — постоянная величина.

 

Кроме того, справедлива следующая теорема.

ТЕОРЕМА 2. Дисперсия числа появлений события А в n независимых испытаниях с вероятностью появления р в каждом из них этого события вычисляется по формуле

D(Х)=n∙р∙(1 – p)=n∙p∙q .  (14)

Приведем здесь еще два важных результата: для случайной величины, распределенной по закону Пуассона (4):  математическое ожидание и дисперсия равны параметру данного распределения.

 

ПРИМЕР 9 (ПРОДОЛЖЕНИЕ). Найти дисперсию числа выигрышных лотерейных билетов по данным примера 9.

 

РЕШЕНИЕ. Имеем 200=n независимых испытаний с вероятностью появления выигрышного билета р=0,015. Следовательно, q=1-0,015=0,985. Тогда по теореме 2 получаем искомую дисперсию:

 

D(Х)=200∙0,015∙0,985=2,955.

ПРИМЕР 10. Банк выдал ссуды n разным заемщикам в размере S руб. каждая под ставку ссудного процента r. Найти математическое ожидание и дисперсию прибыли банка, а также условную ставку ссудного процента, если вероятность возврата  ссуды заемщиком равна р.

 

РЕШЕНИЕ. Поскольку заемщики между собой не связаны,  то можно полагать, что мы имеем n независимых испытаний. Вероятность утери ссуды для банка в каждом испытании равна q=1 – p. Пусть Х — число заемщиков, возвративших ссуду с ссудным процентом, тогда прибыль банка определяется формулой:

П =(1+r/100)∙S∙Х – n∙S,

 

где Х является случайной величиной с биномиальным законом распределения.

 

Тогда, согласно теореме 1, математическое ожидание прибыли определяется с использованием формулы (7) и свойств математического ожидания. Применяя свойства математического ожидания, имеем:

M(П)=(1+r/100)∙S∙M(Х) – n∙S=(1+r/100)∙S∙n∙p – n∙S=((1+r/100)∙p – 1)∙n∙S=(r∙p/100 – q)∙n∙S.   

Поскольку выдача ссуды имеет смысл лишь при положительном математическом ожидании прибыли (положительная средняя величина прибыли), то из условия М(П)>0 вытекает условие на ставку ссудного процента:

 

(1+r/100)∙p – 1>0.   

Отсюда находим:

 

r>100∙(1 – p)/p=100∙q/p.

Дисперсия прибыли банка находится, согласно теореме 2, с использованием формулы (14) и свойств дисперсии:  

D(П)=((1+r/100)∙S)²∙D(Х)= (1+r/100)²∙S²∙n∙p∙q.

СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ.

Одной из основных оценок рассеяния возможных значений случайной величины служит среднее квадратическое отклонение.

 

КАК ОПРЕДЕЛЯЕТСЯ СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

ОПРЕДЕЛЕНИЕ 4. Средним квадратическим отклонением случайной величины Х (стандартом) называется квадратный корень из ее дисперсии:

 

σ(Х)=√D(X) . (15)

Согласно этому определению, из свойства 3 и формулы (13) следует, что в случае суммы взаимно независимых случайных величин справедлива формула

σ²(Х₁+Х₂+… +Х_m)= σ²(Х₁)+ σ²(Х₂) + … + σ²(X_m).  

ПРИМЕР 11. Найти дисперсию и среднее квадратическое отклонение случайной величины Х, заданной следующим распределением:

X	-5	2	3	4	6
P	0,1	0,2	0,3	0,3	0,1

 

РЕШЕНИЕ. Сначала вычислим математическое ожидание случайной величины X. Пользуясь данными из таблицы распределения случайной величины X, находим:

 

М(Х) = (-5)∙0,1+2∙0,2+3∙0,3+4∙0,3+6∙0,1=-0,5+0,4+0,9+1,2+0,6=2,6.

Затем составим таблицу распределения случайной величины Х²:

X2	25	4	9	16	36
P	0,1	0,2	0,3	0,3	0,1

 

Отсюда получаем, что

 

М(Х²)= 25∙0,1+4∙0,2+9∙0,3+16∙0,3+36∙0,1=2,5+0,8+2,7+4,8+3,6=14,4.

По формулам (11) и (15) окончательно получаем искомые значения дисперсии D(X) и среднего квадратического отклонения:

 
D(Х)=М(Х²) — [(М(Х)]²= 14,4 – (2,6)²=14,4 – 6,76=7,64.

σ(Х)=√D(X)=√7,64≈ 2,764.

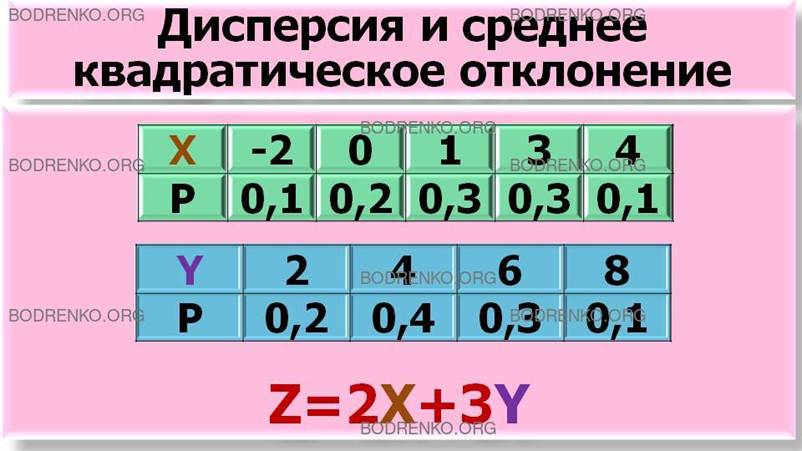
ПРИМЕР 12. Законы распределения независимых случайных величин Х и Y приведены соответственно в таблицах:

X	-2	0	1	3	4
P	0,1	0,2	0,3	0,3	0,1

 

Y	2	4	6	8
P	0,2	0,4	0,3	0,1

Найти дисперсию и среднее квадратическое отклонение случайной величины Z=2Х+3Y.

РЕШЕНИЕ. Согласно свойствам 2 и 3 дисперсии (формулы (12) и (13)), имеем

D(Z)= D(2X+3Y)=4∙D(Х)+9∙D(Y).

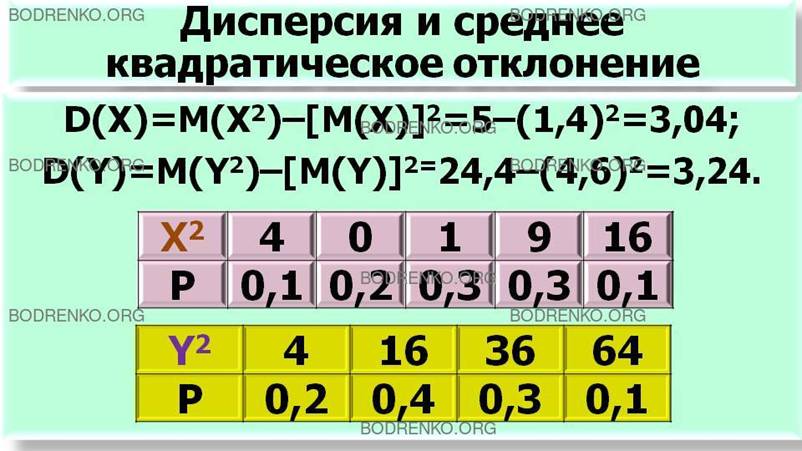
Для вычисления дисперсий D(X)и D(Y) составляем соответствующие таблицы — законы распределения случайных величин Х² и Y² . Мы имеем:

 

X2	4	0	1	9	16
P	0,1	0,2	0,3	0,3	0,1

 

Y2	4	16	36	64
P	0,2	0,4	0,3	0,1

 

Отсюда получаем

D(Х)=М(Х²) – [М(Х)]²=5 – (1,4)²=3,04;

D(Y)=М(Y²) – [М(Y)]²⁼24,4 – (4,6)²= 3,24.

Искомые дисперсия и среднее квадратическое отклонение случайной величины равны:

D(Z)= D(2X+3Y)=4∙D(Х)+9∙D(Y)=4∙3,04+9∙3,24=12,16+29,16=41,32.

σ(Z)= √41,32≈6,428.

ПРИМЕР 10 (ПРОДОЛЖЕНИЕ).  В условиях примера 10 найти математическое ожидание и среднее квадратическое отклонение прибыли при n=1000, р=0,8,  S=100 тыс. руб.,  и r=30% годовых.

РЕШЕНИЕ. Сначала проверим то, что ставка ссудного процента удовлетворяет условию, чтобы математическое ожидание прибыли было положительным:

r>100∙(1 – p)/p=100∙q/p.

В условиях задачи имеем:

 

30>100∙(1 – 0,8)/0,8=20/0,8=25.

 

Таким образом, 30>25, следовательно, условие выполнено.

Вычислим математическое ожидание прибыли:

M(П)=(r∙p/100 – q)∙n∙S=(30∙0,8/100 – 0,2)∙1000∙0,1= 4 (млн. руб.).   

Дисперсия  прибыли равна:  

D(П)=(1+r/100)²∙S²∙n∙p∙q=(1+30/100)²∙(0,1)²∙1000∙0,8∙0,2=1,69∙0,01∙1000∙0,16=2,704.

Теперь найдем среднее квадратическое отклонение прибыли:

σ(П)=√D(П)=√2,704=1,644384 (млн. руб.).

НАЧАЛЬНЫЕ И ЦЕНТРАЛЬНЫЕ МОМЕНТЫ.

 
ОПРЕДЕЛЕНИЕ 5. Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Х^k:

ν_k=М(Х^k). (16)

В частности,

ν₁=М(Х),

 

ν₂=М(Х²).

 

и тогда формула (11) для вычисления дисперсии принимает вид

D(X)=ν₂ – (ν₁)².  (17)

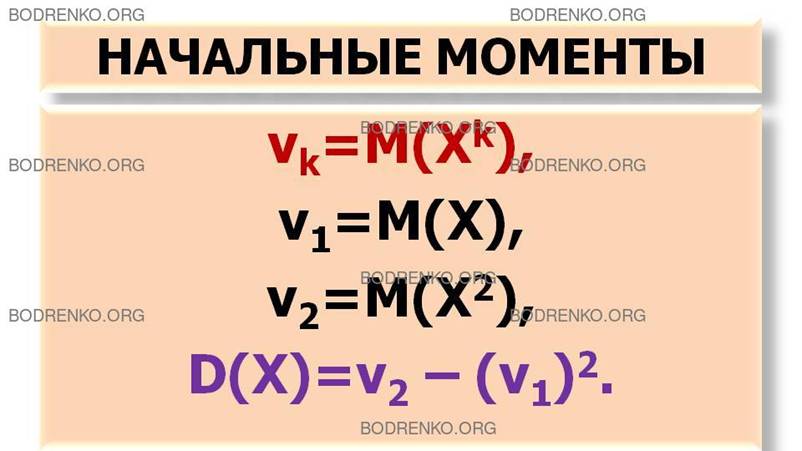
ОПРЕДЕЛЕНИЕ 6. Центральным моментом порядка  k случайной величины Х называется математическое ожидание k-й степени отклонения:

 

μ_k=M[(X – M(X))^k] . (18)

В частности, согласно формуле (9),

 

μ₁=0,

 

а дисперсия случайной величины Х является центральным моментом второго порядка:

D(X)=μ₂=M[(X – M(X))²] .   (19)

Таким образом,

 

μ₂=ν₂ – (ν₁)².  

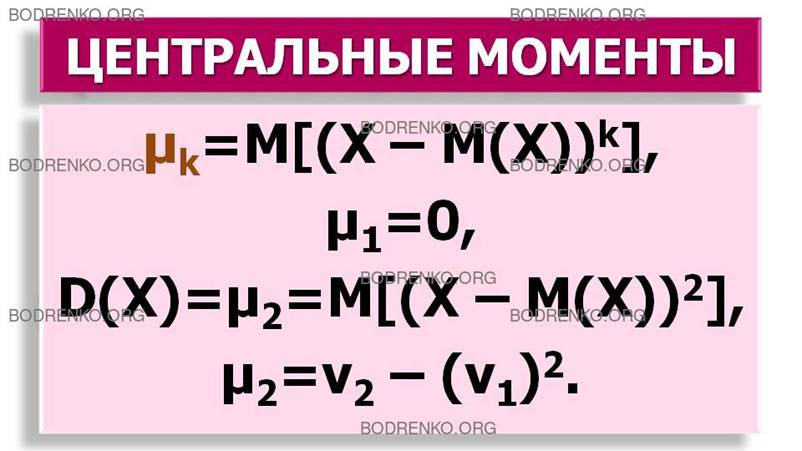
Соотношения, связывающие начальные и центральные моменты, также могут быть легко получены.

Приведем их здесь для моментов третьего и четвертого порядков (они наряду с моментами первого и второго порядков широко применяются в статистике):

μ₃=ν₃ – 3∙ν₂∙ν₁ +2∙(ν₁)³.  

 

μ₄=ν₄ – 4∙ν₃∙ν₁ +6∙ν₂∙(ν₁)² – 3∙(ν₁)⁴.  

Моменты более высоких порядков применяются крайне редко. Моменты, рассмотренные в этом разделе, называют теоретическими. В отличие от них, моменты, вычисляемые по данным наблюдений в математической статистике, называют «эмпирическими».

 

НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

 

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ  НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕЕ СВОЙСТВА.

 
Пусть Х — непрерывная случайная величина, значения которой сплошь заполняют числовой интервал (a, b). Теперь уже нельзя составить перечень всех возможных значений Х, так это было сделано в случае дискретной случайной величины. Тем не менее, существует способ задания любых видов случайных величия.

Пусть х — действительное число. Обозначим вероятность события того, что Х примет значение, меньшее х, через F(х).

 

ЧТО НАЗЫВАЕТСЯ ФУНКЦИЕЙ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 
ОПРЕДЕЛЕНИЕ 1. Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что Х примет значение, меньшее х:

F(х)= Р(Х<х). (20)

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ F(Х)?

 

F(x) – это вероятность того, что случайная величина Х примет значение, которое изображается точкой на числовой оси, расположенной левее точки х.

 

По виду функции F(х) определяется и вид случайной величины.

 

КАКИМИ СВОЙСТВАМИ ОБЛАДАЕТ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

Функция распределения обладает рядом фундаментальных свойств, указанных ниже.

СВОЙСТВО 1. Область значений функции распределения F(x) лежит на отрезке [0,1]:

0≤F(х)≤1.

СВОЙСТВО 2. Функция распределения является неубывающей, т.е.

F(х₂)≥F(х₁) при х₂>x₁.

 

СВОЙСТВО 3. Если возможные значения случайной величины находятся на интервале (а, b), то

 

F(x)=0  при x≤a,

 

и

F(x)=1 при x≥b.

 
Из указанных свойств вытекают важные следствия.

 

1. Вероятность того, что случайная величина Х принимает значения, заключенные внутри интервала (α, β),  равна разности значений функции распределения на концах этого интервала:

P(α≤Х<β) = F(β) – F(α). (21)

 

2. Вероятность того, что непрерывная случайная величина Х примет одно определенное  значение, равна нулю.

3. Если возможные значения непрерывной случайной величины Х расположены на всей числовой оси, то

 

lim F(х)=0,

x→-∞

 

и

 

lim F(x)=1.

x→+∞

ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ И ЕЕ СВОЙСТВА.

 

ЧТО ТАКОЕ ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ?

 

ОПРЕДЕЛЕНИЕ 3. Производная от функции распределения непрерывной случайной величины Х называется плотностью распределения вероятностей Х:

 

f(x)=F`(х). (22)

 

Из этого определения следует, что функция распределения является первообразной для плотности распределения или неопределенным интегралом от нее.

 

Плотность распределения – это скорость изменения вероятности Р(Х<х).

 

Из свойства 2 функции распределения следует справедливость следующей фундаментальной

теоремы.
 

ТЕОРЕМА 3. Вероятность того, что непрерывная случайная  величина Х примет значение на интервале (α, β), определяется по формуле

                  

        β
Р(α<Х<β) = ∫ f(х) dx. (23)

                  α

Вспоминая геометрический смысл определенного интеграла, можно сказать, что вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (α, β), равна площади криволинейной трапеции, ограниченной сверху кривой плотности распределения f(х), снизу – осью Оx, а с краев — вертикальными прямыми х =α‚ и х=β (рисунок 1).

 

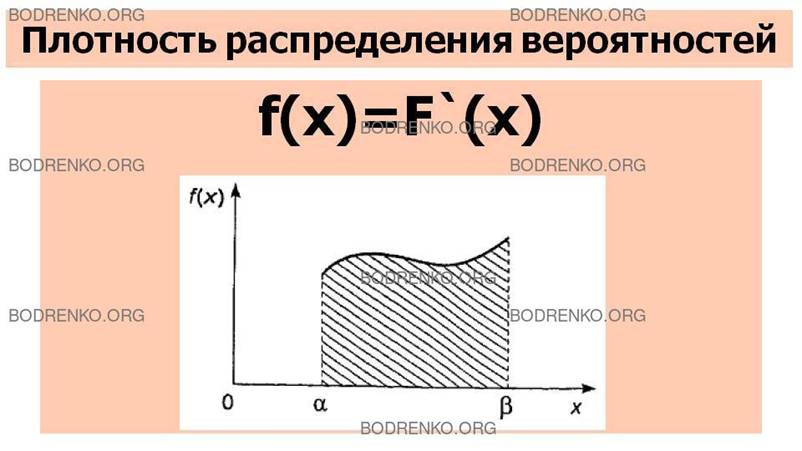
Рисунок 1.

 

Связь между функцией распределения и плотностью распределения вероятностей устанавливается, согласно (22), формулой

 

                      x

F(х)=P(Х<х) = ∫f(x) dx. (24)
                       -∞

ПРИМЕР 13. Случайная величина Х задана функцией распределения

F(x)=0, x≤0;

 

F(x)=sin (x), 0<x≤π/2;

F(х)=1, x>π/2.

Найти плотность распределения Х.

 

РЕШЕНИЕ. Функция F(х) является кусочно-дифференцируемой. Согласно формуле (22), дифференцируя F(х) по интервалам ее задания, получаем:

 

f(x)=F`(x)=0, x≤0;

 

 

f(x)=F`(x)=cos(x), 0<x≤π/2;

 

 

f(x)=F`(x)=0, x>π/2.

 

ПРИМЕР 3. Непрерывная случайная величина Х задана плотностью распределения на всей числовой оси:

 

f(x)=(1/π)∙(1/(1+x²)).

 

Найти вероятность того, что Х примет значение на интервале ( - 1, 1).

 

РЕШЕНИЕ. Согласно формуле (23), искомая вероятность  равна

 

         1
Р(-1<Х<1) = ∫ (1/π)∙(1/(1+x²))dx =(1/π)∙(arctg(1) – arctg(-1))=(1/π)∙(π/4 – (-π/4))=1/2.  

                  -1

КАКИМИ СВОЙСТВАМИ ОБЛАДАЕТ ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ?

 

Плотность распределения обладает рядом свойств, основные из них указаны ниже.

СВОЙСТВО 1. Плотность распределения является неотрицательной функцией:

 

f(X)≥0.

Это следует из характера функции распределения: она является неубывающей, и, значит, ее производная неотрицательна.

 

СВОЙСТВО 2. Несобственный интеграл от плотности распределения в пределах интегрирования по всей числовой оси равен единице:

 

+∞

∫f(x) dx.  =1.

 -∞

                             

Это равенство означает достоверность события, что случайная величина Х примет значение, принадлежащее интервалу (- ∞; +∞), т.е. вероятность этого события Р(-∞<Х<+∞)=1.

 

Так, если все возможные значения случайной величины Х лежат внутри интервала (a; b), то

b

∫f(x) dx =1.

a

 

(25)

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

Определения числовых характеристик дискретных случайных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (5) и (10) берутся их интегральные аналоги. 

КАК ОПРЕДЕЛЯЕТСЯ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

ОПРЕДЕЛЕНИЕ 4. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой находятся на отрезке [а,b], называется определенный интеграл:

          b

M(X)= ∫ x∙f(x) dx.  (26)

          a

В том случае, когда возможные значения случайной величины Х заполняют всю ось Ох, пределы интегрирования а и b бесконечны: а = -∞, b=+∞. Возможны также случаи, когда один из пределов интегрирования бесконечен (возможные значения Х лежат на полупрямой).

КАК ОПРЕДЕЛЯЕТСЯ ДИСПЕРСИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

ОПРЕДЕЛЕНИЕ 5. Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения:

          b

D(x)= ∫ [x – M(X)]²∙f(x)∙dx.  (27)

          a

Все сказанное выше о случаях бесконечных пределов интегрирования остается справедливым и для дисперсии.

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и прежде, по формуле (15):

 σ(Х)=√D(X).

Для вычисления дисперсии употребляется более удобная формула, которая выводится из (27):

          b

D(X)= ∫ x²∙f(x)∙dx – [M(X)]².  (28)

          a

ПРИМЕР 14. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной плотностью распределения на отрезке [0,1]:

f(х)=1, хÎ[0,1].

РЕШЕНИЕ. Согласно формулам (26), (28) и (15) последовательно вычисляем искомые величины:

 

          1

M(X)= ∫ x∙1∙dx = 1/2.  

          0

 

          1

D(X)= ∫ x²∙1∙dx – [1/2]²=1/3-1/4=1/12.

          0

σ(Х)=√D(X)= √(1/12)≈0,289.

ПРИМЕР 15. Найти основные числовые характеристики непрерывной случайной величины Х,  заданной функцией распределения на положительной полуоси Ох:

F(х)=1 – exp{-x}, х Î(0, +∞).

РЕШЕНИЕ. Найдем сначала плотность распределения:

f(x)=F`(х)=exp{-x}, хÎ(0,+∞).

Затем, как и в предыдущем примере, вычисляем соответствующие интегралы; при их вычислении  применяем правило интегрирования по частям для определенного интеграла. В итоге  получаем искомые величины:

         +∞

M(X)= ∫ x∙exp{-x}∙dx =1.  

          0

 

          +∞

D(X)= ∫ x²∙exp{-x}∙dx – [1]²= 2 – 1=1.

          0

 

σ(Х)=√D(X)=1.

ОСНОВНЫЕ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

КАКОЕ  РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НАЗЫВАЕТСЯ РАВНОМЕРНЫМ?
 
ОПРЕДЕЛЕНИЕ 1. Распределение вероятностей называется равномерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.

Пусть на интервале (а, b) плотность распределения является постоянной величиной: f(х)=С. Определим значение С из условия (25):

 

b

∫f(x) dx =1.

a

 

Отсюда получаем, что

C∙(b – a)=1,  

С=1/(b – a).

Значит, искомая плотность равномерного распределения дается формулой (29):

f(x)=0, x≤a;

 
f(х)=1/(b – a), a<х≤b;

f(x)=1, х>b.

График плотности равномерного распределения указан на рисунке 2.

Рисунок 2. График плотности равномерного распределения.

ПРИМЕР 16. Найти среднеквадратическое отклонение случайной величины Х, распределенной равномерно на интервале (1,5).

РЕШЕНИЕ. Согласно формуле (29), плотность распределения указанной случайной величины является ненулевой и равна ¼=0,25 на интервале (1,5).

По формулам (26) и (28)  последовательно вычисляем:

           5

M(X)= ∫ x∙(1/4)∙dx=(1/4)∙(25/2 – 1/2)=12/4=3.  

          1

          5

D(X)= ∫ x²∙(1/4)∙dx – [3]²=(1/4)∙(125/3 – 1/3) – 9=124/12 – 9=31/3 – 9=4/3.

          1

 

σ(Х)=√(4/3)=2/√3≈1,155.

КАКОЕ  РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НАЗЫВАЕТСЯ НОРМАЛЬНЫМ?

ОПРЕДЕЛЕНИЕ. Общим нормальным распределением вероятностей непрерывной случайной величины Х называется распределение с плотностью

f(х)=(1/(σ∙√(2π)))∙exp{-(x - a)²/(2∙σ²)}      . (30)

Нормальное распределение задается двумя параметрами: a и σ.

Согласно определениям математического ожидания и дисперсии (формулы (26) и (28)), после выполнения соответствующих интегрирований можно вывести, что для нормального распределения справедливы следующие формулы.

М(Х)=a,

D(Х)=σ²,

σ(Х)=σ.

КАКОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НАЗЫВАЕТСЯ НОРМИРОВАННЫМ?

ОПРЕДЕЛЕНИЕ. Нормальное распределение с параметрами a=0 и σ=1 называется нормированным; его плотность равна

f(х)=(1/√(2π))∙exp{-x ²/2}      . (31)

Рассмотрим функцию нормального распределения как первообразную плотности распределения вероятностей. Для случая нормированного нормального распределения (31) она, согласно формуле (24), имеет вид

                      x             x

F(х)=P(Х<х) = ∫f(z)∙dz = ∫ (1/√(2π))∙exp{-z ²/2}dz  . (32)
                       -∞            -∞

                                             

Поскольку функция f(x) (31) является четной, то неопределенный интеграл от нее является нечетной функцией, и потому вместо функции распределения (32) используется функция Лапласа:

                        x            

Φ(х)= (1/√(2π))∙ ∫exp{-z ²/2}∙dz  . (33)
                           0

ЗАМЕЧАНИЕ. Функции (31) и (33) табулированы.  Их значения находятся по специальным таблицам.

График плотности нормального распределения (30) для разных значений σ  показан на рисунке 3.

Рисунок 3.

ЧТО ТАКОЕ МОДА НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

ОПРЕДЕЛЕНИЕ. Модой Мo(Х) называется возможное значение случайной величины Х, при котором плотность распределения имеет максимум.

ЧТО ТАКОЕ МЕДИАНА НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

ОПРЕДЕЛЕНИЕ. Медианой Ме(Х) называется такое возможное значение случайной величины Х, что вертикальная прямая  х=Ме(Х) делит пополам площадь, ограниченную кривой плотности распределения.

 Нетрудно видеть, что график плотности нормального распределения симметричен относительно прямой х=a, и потому  и мода и медиана в данном случае совпадают с математическим ожиданием:

 
Mo(X)=Me(X)=М(Х)=a.

Пусть случайная величина Х задана плотностью нормального распределения (30), тогда вероятность того, что Х примет значение на интервале (α, β), согласно формуле (23), равна:

                                     β
Р(α<Х<β) =(1/(σ∙√(2π)))∙∫ exp{-(x - a)²/(2∙σ²)}∙dx.

                                    α

Преобразование этой формулы путем введения новой переменной интегрирования

z=(х - a)/σ

приводит к удобной вычислительной  формуле:

Р(α<Х<β) =Φ((β – a)/σ) – Φ((α –a)/σ),  (18.44)

 

где Ф — функция Лапласа, определенная по формуле (33).

ПРИМЕР 17. Случайная величина распределена по нормальному закону с математическим ожиданием и средним квадратическим отклонением, соответственно равными 10 и 5. Найти вероятность того, что Х примет значение на интервале (20,30).

РЕШЕНИЕ. Воспользуемся формулой (34). По условию задачи имеем:

а=10,σ=5, α=20 и β=30.

 

Следовательно,

Р(20<Х<30) =Φ((30 –10)/5) – Φ((20 –10)/5) =Φ(4) – Φ(2).

 

По специальной таблице находим соответствующие значения функции Лапласа и окончательно получаем

Р(20<Х<30)=0,5 – 0,4772=0,0228.

ПРИМЕР 18. Магазин производит продажу мужских костюмов. По данным статистики, распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, соответственно равными 48 и 2. Определить процент спроса на 50-й размер при условии разброса значений этой величины в интервале (49,51).

 

РЕШЕНИЕ. По условию задачи имеем:

а=48, σ=2, α=49, β=51.

 

Используя формулу (34), получаем, что вероятность спроса  на 50-й размер в заданном интервале равна:

Р(49<Х<50)=Ф((51–48)/2) – Ф((49–48)/2)= Ф(1, 5) – Ф(0,5)=0,4332 – 0,1915 = 0,2417.

Следовательно, спрос на 50-й размер костюмов составит около 24%, и магазину нужно предусмотреть это в общем объеме закупки.

АСИММЕТРИЯ И ЭКСЦЕСС.

В прикладных задачах, например в математической статистике, при теоретическом изучении эмпирических распределений, отличающихся от нормального распределения, возникает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.

ЧТО ТАКОЕ АСИММЕТРИЯ ТЕОРЕТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ?

 

ОПРЕДЕЛЕНИЕ. Асимметрией теоретического распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

Аs=μ₃/σ³. (35)

ЧТО ТАКОЕ ЭКСЦЕСС ТЕОРЕТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ?

 

ОПРЕДЕЛЕНИЕ. Эксцессом теоретического распределения называется величина, определяемая равенством

Еk= μ₄/σ⁴ – 3, (36)

где μ₄  – центральный момент четвертого порядка.

ЧЕМУ РАВНЫ АСИММЕТРИЯ И ЭКСЦЕСС ДЛЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ?

 

Для нормального распределения Аs=Ek=0.

 

При отклонении от нормального распределения асимметрия  положительна, если «длинная» и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствующей моде (рисунок 4).

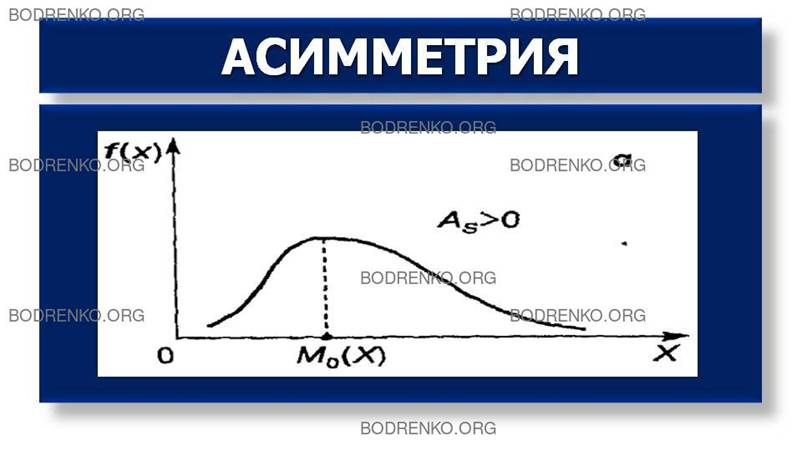
Рисунок 4.

 

Если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рисунок 5).

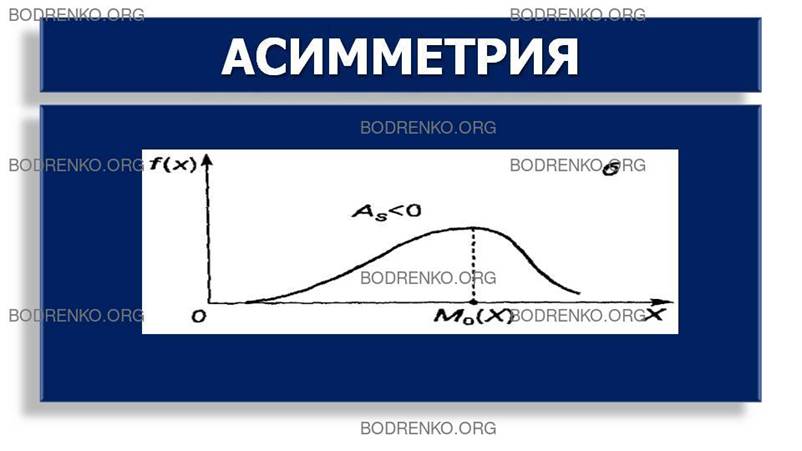
Рисунок 5. 

 

ЧТО ХАРАКТЕРИЗУЕТ ЭКСЦЕСС?

 

Эксцесс характеризует «крутизну» подъема кривой распределения по сравнению с нормальной кривой. Если эксцесс положителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину (рисунок 6).

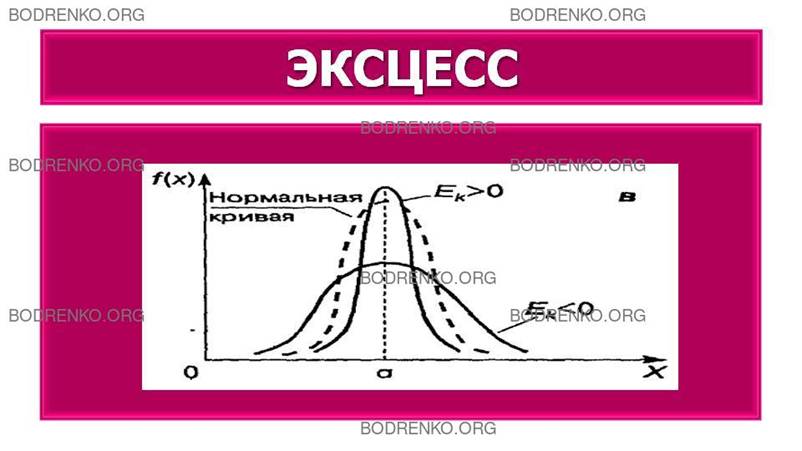
Рисунок 6.

РАЗДЕЛ 2. ОСНОВНЫЕ ПОНЯТИЯ МАРКОВСКИХ СЛУЧАЙНЫХ  ПРОЦЕССОВ.

 

КАКАЯ ФУНКЦИЯ НАЗЫВАЕТСЯ СЛУЧАЙНОЙ?

 

Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной.

 

ЧТО ТАКОЕ СЛУЧАЙНЫЙ ПРОЦЕСС?

 

Случайная функция X(t), аргументом которой является время, называется случайным процессом.

 

КАКОЙ СЛУЧАЙНЫЙ ПРОЦЕСС НАЗЫВАЕТСЯ МАРКОВСКИМ?

 

Марковские процессы являются частным видом случайных процессов. Особое место марковских процессов среди других классов случайных процессов обусловлено следующими обстоятельствами:

 

- для марковских процессов хорошо разработан математический аппарат, позволяющий решать многие практические задачи;

 

- с помощью марковских процессов можно описать (точно или приближенно) поведение достаточно сложных систем.

 

ОПРЕДЕЛЕНИЕ. Случайный процесс, протекающий в какой-либо системе S, называется марковским (или процессом  без последействия), если он обладает следующим свойством: для любого момента времени t₀ вероятность любого состояния системы в будущем (при t>t₀) зависит только от ее состояния в настоящем (при t =t₀),  и  не зависит от того, когда и каким образом система S пришла в это состояние.

 

КЛАССИФИКАЦИЯ МАРКОВСКИХ ПРОЦЕССОВ.

 

Классификация марковских случайных процессов производится в зависимости от непрерывности или дискретности множества значений функции X(t) и параметра t.

 

Различают следующие основные виды марковских случайных процессов:

 

- с дискретными состояниями и дискретным временем (цепь  Маркова);

 

-  с непрерывными состояниями и дискретным временем (марковские последовательности);

 

-  с дискретными состояниями и непрерывным временем (непрерывная цепь Маркова);

 

-  с непрерывным состоянием и непрерывным временем.

 

На этой лекции мы рассмотрим только марковские процессы с дискретными состояниями S₁, S₂, ..., S_n.

 

ЧТО ТАКОЕ ГРАФ СОСТОЯНИЙ?

 

Марковские процессы с дискретными состояниями удобно иллюстрировать с помощью, так называемого графа состояний (рисунок 7), где кружками обозначены состояния S1, S2, ... системы S, а стрелками — возможные переходы из состояния в состояние. На графе отмечаются только непосредственные переходы, а не переходы через другие состояния. Возможные задержки в прежнем состоянии изображают «петлей», т. е. стрелкой, направленной из данного состояния в него же. Число состояний системы может быть как конечным, так и бесконечным (но счетным). Пример графа состояний системы S представлен на рисунке 7.

 

Рисунок 7. Граф состояний системы S.

 

КАКОЙ МАРКОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС НАЗЫВАЕТСЯ МАРКОВСКОЙ ЦЕПЬЮ?

 

Марковский случайный процесс с дискретными состояниями и дискретным временем называют марковской цепью.

 

Для такого процесса моменты t₁, t₂, ..., когда система S может менять свое состояние, рассматривают как последовательные шаги процесса. А в качестве аргумента, от которого зависит процесс, выступает не время t, а номер шага 1,2,..., k, и т.д. Случайный процесс в этом случае характеризуется последовательностью состояний S(0), S(1), S(2), ..., S(k), ...,  где S(0) — начальное состояние системы (перед первым шагом); S(1) - состояние системы после первого шага; S(k) - состояние системы после k-го шага, и т.д.

 

Событие {S(k)=S_i}, состоящее в том, что сразу после k-го шага система находится в состоянии S_i (i=1, 2, ...), является случайным событием.

 

Последовательность состояний S(0), S(1), ..., S(k), ...,  можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния S_i в любое S_j не зависит от того, когда и как система пришла в состояние S_i. Начальное состояние S(0) может быть  заданным заранее или случайным.

 

ЧТО ТАКОЕ ВЕРОЯТНОСТИ СОСТОЯНИЙ ЦЕПИ МАРКОВА?

 

Вероятностями состояний цепи Маркова называются вероятности P_i(k) того, что после k-го шага (и до (k+1)-го) система S будет находиться в состоянии S_i (i=1, 2, ..., n).

 

Очевидно, для любого k выполнено равенство:

 

n

∑ P_i(k) = 1.  

i=1

 

 

ЧТО НАЗЫВАЕТСЯ НАЧАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ ВЕРОЯТНОСТЕЙ МАРКОВСКОЙ ЦЕПИ?

 

Начальным распределением вероятностей марковской цепи называется распределение вероятностей состояний в начале процесса:

 

P₁(0), P₂(0), ..., P_i(0), ..., Р_n(0) .   (*)

 

В частном случае, если начальное состояние системы S в точности известно S(0)=S_i, то начальная вероятность Р₁(0)=1, а все остальные начальные вероятности равны нулю.

 

 

ЧТО ТАКОЕ ПЕРЕХОДНАЯ ВЕРОЯТНОСТЬ?

 

Вероятностью перехода (переходной вероятностью) на  k-м шаге из состояния S_i в состояние S_j называется условная вероятность того, что система S после k-го шага окажется в состоянии S_j при условии, что непосредственно перед этим (после (k – 1)-го шага) она находилась в состоянии S_i.

 

ЧТО ТАКОЕ ПЕРЕХОДНАЯ МАТРИЦА? 

 

Поскольку система может пребывать в одном из n состояний, то для каждого момента времени t необходимо задать n² вероятностей перехода P_ij, которые удобно представить в виде следующей  матрицы:

 

P11	P12	…	P1j	…	P1n
P21	P22	…	P2j	…	P2n
…	…	…	…	…	…
Pi1	Pi2	…	Pij	…	Pin
…	…	…	…	…	…
Pn1	Pn2	…	Pnj	…	Pnn

 

где P_ij  - это вероятность перехода за один шаг из состояния S_i в состояние S_j, P_ii — это вероятность задержки системы в состоянии Si.

 

Матрица ||P_ij||  называется переходной или матрицей переходных вероятностей.

КАКАЯ МАРКОВСКАЯ ЦЕПЬ НАЗЫВАЕТСЯ ОДНОРОДНОЙ?

 

Если переходные вероятности не зависят от номера шага (от времени), а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая цепь Маркова называется однородной.

 

КАКОВЫ  СВОЙСТВА ПЕРЕХОДНОЙ МАТРИЦЫ ОДНОРОДНОЙ МАРКОВСКОЙ ЦЕПИ?

 

Переходные вероятности однородной марковской цепи Р_ij  образуют квадратную матрицу размера n x n. Отметим некоторые ее  особенности:

 

1. Каждая i-я строка матрицы характеризует выбранное состояние системы (i-е). Элементы i-той строки представляют собой вероятности всех возможных переходов за один шаг из выбранного (из i-го) состояния, в том числе и переход в самое себя.

 

2. Элементы каждого j-го столбца показывают вероятности всех возможных переходов системы за один шаг в заданное (j-е) состояние.

 

Другими словами, i-я строка характеризует вероятность перехода системы из i-го состояния, j-й столбец  - вероятность перехода в j-е состояние.

 

3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий.

 

4. По главной диагонали матрицы переходных вероятностей стоят вероятности Р_ii того, что система не выйдет из состояния S_i, а останется в нем.

 

КАК ОПРЕДЕЛЯЮТСЯ ВЕРОЯТНОСТИ СОСТОЯНИЙ СИСТЕМЫ ДЛЯ ОДНОРОДНОЙ МАРКОВСКОЙ ЦЕПИ?

 

Если для однородной марковской цепи заданы начальное распределение вероятностей (*) и матрица переходных вероятностей  ||Pij||, то вероятности состояний системы P_i(k) (i=1, …, n; j=1, …, n)  определяются по рекуррентной формуле:

 

РАЗДЕЛ 3. НЕПРЕРЫВНЫЕ ЦЕПИ МАРКОВА.

 

ЧТО ТАКОЕ НЕПРЕРЫВНАЯ ЦЕПЬ МАРКОВА?

 

Марковский случайный процесс с дискретными состояниями и  непрерывным временем называется непрерывной цепью Маркова при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.

 

В экономике часто встречаются ситуации, которые указать заранее невозможно. Например, любая деталь или агрегат автомобиля могут выйти из строя в любой, непредсказуемый заранее момент времени. Для описания таких систем в отдельных случаях можно использовать математический аппарат непрерывной цепи Маркова.

 

Пусть система характеризуется  состояниями S₀, S1, S₂, ..., S_n. При этом переход из состояния в состояние может осуществляться в любой момент времени.

 

Обозначим через Р_i(t) вероятность того, что в момент времени t система S будет находиться в состоянии S_i (i=0,1, ..., n). Требуется определить для любого t вероятности состояний

 Р₀(t), P₁(t), ..., P_n(t).

 

Очевидно, что выполняется равенство:

 

n

∑ P_i(t) = 1.  

i=0

 

ЧТО ТАКОЕ ПЛОТНОСТИ ВЕРОЯТНОСТЕЙ ПЕРЕХОДА?

 

Для процесса с непрерывным временем вместо переходных вероятностей P_ij рассматриваются плотности вероятностей перехода λ_ij, представляющие собой предел отношения вероятности перехода системы за время Δt из состояния S_i в состояние S_j к длине промежутка Δt:

 

где  P_ij(t; Δt) — вероятность того, что система, пребывавшая в момент t в состоянии Si, за время Δt перейдет из него в состояние Sj (при этом всегда i≠j).

 

Если λij=const, то процесс называется однородным, если плотность вероятности зависит от времени λij=λij(t), то - неоднородным.

 

 

ЧТО ТАКОЕ ПОТОК СОБЫТИЙ?

 

При рассмотрении непрерывных марковских процессов принято представлять переходы системы S из состояния в состояние как происходящие под влиянием некоторых потоков событий.

 

Потоком событий называется последовательность однородных событий, следующих одно за другим через какие-то, вообще говоря, случайные интервалы времени.

 

Плотность вероятности перехода интерпретируется как интенсивность λij соответствующих потоков событий.

 

Если все эти потоки пуассоновские, то процесс, протекающий в системе S, будет марковским.

 

КАКОЙ ГРАФ СОСТОЯНИЙ СИСТЕМЫ НАЗЫВАЮТ РАЗМЕЧЕННЫМ?

 

При изучении марковских случайных процессов с дискретными состояниями и непрерывным временем в графе состояний над стрелками, ведущими из состояния S_i в S_j, проставляют соответствующие интенсивности λ_ij. Такой граф состояний называют размеченным.

 

Пусть система S имеет конечное число состояний S₀, S₁, ..., S_n. Случайный процесс, протекающий в этой системе, описывается вероятностями состояний P₀(t), P₁(t), ... Р_n(t), где Р_i(t) — вероятность того, что система S в момент t находится в состоянии S_i.

 

Для любого t выполнено равенство:

 

n

∑ P_i(t) = 1.  

i=0

 

Вероятности состояний Р_i(t) находят путем решения системы дифференциальных уравнений (уравнений Колмогорова), имеющих вид:

где i=0,1, ..., n.

 

ЧТО ТАКОЕ ПОТОК ВЕРОЯТНОСТИ ПЕРЕХОДА?

 

Величина λ_ij∙P_i(t) называется потоком вероятности перехода из состояния S_i в S_j,  причем интенсивность потоков λ_ij может зависеть от времени или быть постоянной.

 

Уравнения Колмогорова  составляют по размеченному графу состояний системы, пользуясь следующим мнемоническим правилом: производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное состояние, минус сумма всех потоков вероятности, идущих из данного состояния в другие.

 

Чтобы решить систему дифференциальных уравнений Колмогорова, нужно задать начальное распределение вероятностей P₀(0), P₁(0),..., Р_i(0), ..., P_n(0). Для решения применяют численные методы.

 

Рассмотрим еще одну типичную схему непрерывных марковских цепей, так называемую схему гибели и размножения, часто  встречающуюся в разнообразных практических задачах.

 

ЧТО ТАКОЕ ПРОЦЕСС ГИБЕЛИ И РАЗМНОЖЕНИЯ?

 

Марковский процесс с дискретными состояниями S₀, S₁, S₂, ..., S_n называется процессом гибели и размножения, если все состояния можно вытянуть в одну цепочку так, что:

 

-  каждое из средних  состояний (S₁, S₂, ..., S_n-1) может переходить только в соседние состояния, которые, в свою очередь, переходят обратно;

 

- а крайние состояния (S₀ и S_n) переходят только в соседние состояния (рисунок 8).

 

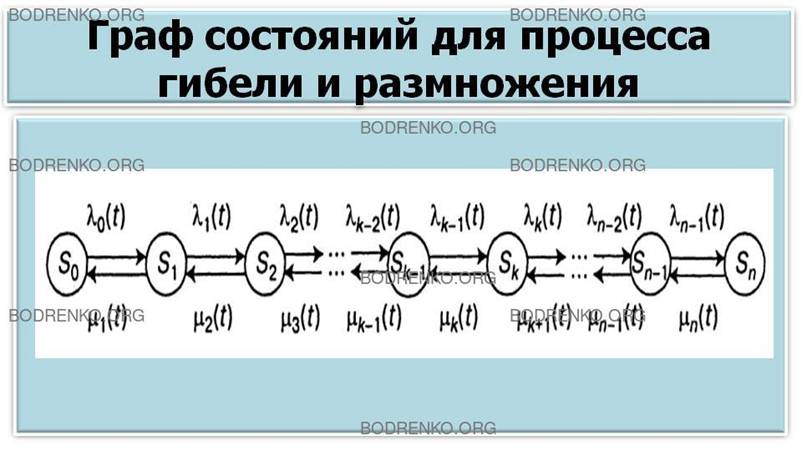
Рисунок 8. Граф состояний для процесса гибели и размножения.

Название взято из биологических задач, где состояние популяции S_k означает наличие в ней k единиц особей. Переход вправо связан с размножением единиц, а влево — с их гибелью.

 

 

λ₀(t), λ₁(t),  …, λ_n-1(t), … - интенсивности размножения,

 

 

μ₁(t), μ₂(t), …,μ_n(t)  -  интенсивности гибели.

 

 

Интенсивности  λ и μ имеют индексы того состояния, из которого стрелка выходит.

 

С состоянием S_k связана неслучайная величина Х_k: если система в момент времени t находится в состоянии S_k,   то дискретная случайная величина X(t), связанная с функционированием системы, принимает значение k. Таким образом, получаем случайный процесс X(t), который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние.

 

Марковским процессом гибели и размножения с непрерывным временем называется такой случайный процесс, который может принимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в любой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным.

 

ЧТО ТАКОЕ ПРОЦЕСС ЧИСТОГО РАЗМНОЖЕНИЯ, ЧИСТОЙ ГИБЕЛИ?

 

В практике встречаются процессы чистого размножения и чистой гибели.

 

Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю.

 

Аналогично процессом чистой гибели называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.

 

КАКИМИ ОСНОВНЫМИ СВОЙСТВАМИ ОБЛАДАЮТ СЛУЧАЙНЫЕ ПОТОКИ СОБЫТИЙ?

 

При исследовании непрерывных марковских цепей, как было уже отмечено, часто бывает удобно представить переход системы из состояния в состояние как воздействие каких-то потоков событий (поток заявок на обслуживание, поток автомобилей, поток документов и т. п.).

 

 

Различают следующие основные свойства, которыми могут обладать случайные потоки событий:

 

- стационарность;

 

- ординарность;

 

- отсутствие последействия.

 

Свойство стационарности проявляется в том, что вероятность попадания того или иного числа событий на участок времени (t, t+τ) зависит только от длины участка τ и не зависит от расположения этого временного участка на оси Ot. Другими словами, стационарность означает неизменность вероятностного режима потока событий во времени. Поток, обладающий свойством стационарности, называют стационарным. Для стационарного потока среднее число событий, воздействующих на систему в течение единицы времени, остается постоянным. Реальные потоки событий в экономике предприятия являются в действительности стационарными лишь на ограниченных участках времени.

 

Свойство ординарности потока присутствует, если вероятность попадания на элементарный участок времени двух и более событий пренебрежимо мала по сравнению с длиной этого участка. Свойство ординарности означает, что за малый промежуток времени практически невозможно появление более одного события. Поток, обладающий свойством ординарности, называют ординарным. Реальные потоки событий в различных экономических системах либо являются ординарными, либо могут быть достаточно просто приведены к ординарным.

 

Отсутствие последействия — это свойство потока, которое состоит в том, что для любых непересекающихся участков времени количество событий, попадающих на один из них, не зависит от того, сколько событий попало на другие участки времени. Поток, обладающий свойством отсутствия последействия, называют потоком без последействия.

 

ЧТО ТАКОЕ ПРОСТЕЙШИЙ ПОТОК СОБЫТИЙ?

 

Поток событий, одновременно обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим потоком событий.

 

ЧТО ТАКОЕ ИНТЕНСИВНОСТЬ ПОТОКА СОБЫТИЙ?

 

Под интенсивностью потока понимают

 

 

 

Где m(t, t+τ) – среднее число событий на временном промежутке (t, t+τ).

 

Для простейшего потока интенсивность λ = const.

 

КАКОЙ ПОТОК СЛУЧАЙНЫХ СОБЫТИЙ НАЗЫВАЮТ НЕСТАЦИОНАРНЫМ ПУАССОНОВСКИМ ПОТОКОМ?

 

Если поток  событий не имеет последействия, ординарен, но не стационарен,  то его называют нестационарным пуассоновским потоком, а его интенсивность зависит от времени, т. е. λ=λ(t).

 

Отметим еще одно важное свойство простейшего потока событий. Промежуток времени t между соседними событиями распределен по показательному закону, а его среднее значение Тср. и среднее  квадратическое отклонение σ равны, т. е.

 

Тср.=σ=1/λ ,

 

где λ – интенсивность потока.

 

Для нестационарного пуассоновского потока закон распределения промежутка t уже не является показательным, так как зависит от положения на оси Оt и вида зависимости λ(t).  Однако для некоторых задач при сравнительно небольших изменениях λ(t) его можно приближенно считать показательным с интенсивностью λ, равной среднему значению λ(t).

 

Таким образом, для исследуемой системы S с дискретными состояниями и непрерывным временем переходы из состояния в состояние происходят под действием пуассоновских потоков событий с определенной интенсивностью λ_ij.

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Бережная Е.В., Бережной В.И. Математические методы моделирования экономических  систем: Учеб. пособие. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. - 432 с.: ил.

 

 [2] Колемаев В.А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем.  М.: ЮНИТИ-ДАНА, 2005. - 295 с.

[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. 4-е изд., испр. – М.: Дело, 2003. – 688 с.

 

[4] Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.

 

[5] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).