Инвестиционный анализ

 

Лекция 7

 

Тема лекции: «Основы анализа инвестиционных рисков»

Разделы лекции:

 

1. Понятие риска и неопределенности. Классификация проектных рисков.

2. Подходы к оценке рисков инвестиционного проекта.

3. Измерение и количественная оценка риска.

РАЗДЕЛ 1. ПОНЯТИЯ РИСКА И НЕОПРЕДЕЛЕННОСТИ. КЛАССИФИКАЦИЯ ПРОЕКТНЫХ РИСКОВ.

 

Начиная рассмотрение вопроса об оценке инвестиционного проекта в условиях неопределенности и риска, необходимо различать понятия «риск» и «неопределенность».

 

Неопределенность предполагает наличие факторов, при которых результаты действий не являются детерминированными (о которых имеется полная и точная информация), а степень возможного влияния этих факторов на результаты неизвестна; это неполнота или неточность информации об условиях реализации проекта.

 

Факторы неопределенности подразделяются на ВНЕШНИЕ и ВНУТРЕННИЕ. Внешние факторы — законодательство, реакция рынка на выпускаемую продукцию, действия конкурентов и др. Внутренние — компетентность персонала фирмы, ошибочность определения характеристик проекта и т. д.

 

КАКОВЫ ОСОБЕННОСТИ УЧЕТА НЕОПРЕДЕЛЕННОСТИ В ИНВЕСТИЦИОННОМ ПРОЕКТЕ?

 

Отметим некоторые важные особенности, связанные с учетом неопределенности в инвестиционном проектировании:

 

- неопределенность нельзя трактовать как отсутствие какой бы то ни было информации об условиях реализации проекта, речь может идти только о неполноте и неточности имеющейся информации. Соответственно учет неопределенности подразумевает сбор и наиболее полное использование всей имеющейся полезной информации об условиях реализации проекта и степени возможности их осуществления. Иными словами, упор делается не на отсутствие, а на наличие информации, и именно эта имеющаяся информация и должна рассматриваться как точная и обоснованная и использоваться при оценке проекта;

 

- неопределенность может относиться не только к информации о будущих условиях реализации проекта, но и к использованной при проектировании информации об уже осуществленных действиях. Поэтому факторы неопределенности необходимо учитывать и при подготовке исходной информации для разработки проекта, и при оценке результатов его реализации, а также при корректировке хода реализации на основе поступающей новой информации.

 

ЧТО ТАКОЕ СИТУАЦИЯ РИСКА?

 

Под риском понимается вероятность возникновения условий, приводящих к негативным последствиям для всех или отдельных участников проекта. Однако приведенное определение не охватывает всего содержания риска. Для более полной характеристики определения «риск» целесообразно выявить понятие ситуация риска.

 

Понятие «ситуация» можно определить как сочетание, совокупность различных обстоятельств и условий, создающих определенную обстановку для того или иного вида деятельности.

 

Среди различных видов ситуаций особое место занимают ситуации риска. Функционированию и развитию многих экономических процессов присущи элементы неопределенности. Это обусловливает появление ситуаций, не имеющих однозначного исхода (решения). Если существует возможность количественно и качественно определять степень вероятности того или иного варианта, то это и будет ситуация риска.

 

ЧЕМ СИТУАЦИЯ РИСКА ОТЛИЧАЕТСЯ ОТ СИТУАЦИИ НЕОПРЕДЕЛЕННОСТИ?

 

Следует отметить, что ситуация риска качественно отличается от ситуации неопределенности. Ситуация неопределенности характеризуется тем, что вероятность наступления результатов решений или событий в принципе невозможно установить. Таким образом, ситуация риска — это разновидность неопределенности, при которой наступление событий вероятно и может быть определено.

 

Влияние факторов риска и неопределенности приводит к тому, что содержание, состав инвестиционного проекта и методы оценки его эффективности существенно изменяются. Основным отличием проектов, разрабатываемых и оцениваемых с учетом неопределенности, является то, что условия их реализации и соответствующие затраты и результаты точно не известны. Поэтому приходится принимать во внимание весь спектр их возможных значений, а также «степень возможности» каждого из них.

 

Из вышесказанного вытекают и другие отличия:

 

1. Необходимость введения новых и обобщения «обычных» показателей эффективности проекта.

 

2. Изменение экономического содержания понятия эффективности проекта.

 

3. Потребность в существенном изменении содержания инвестиционного проекта, прежде всего в части усложнения организационно-экономического механизма его реализации.

 

4. Необходимость введения в рассмотрение дополнительных показателей, характеризующих неопределенность и риск.

 

Рассмотрим эти отличия подробнее.

 

ПОЧЕМУ ВОЗНИКАЕТ НЕОБХОДИМОСТЬ ВВЕДЕНИЯ НОВЫХ ПОКАЗАТЕЛЕЙ?

 

НОВЫЕ ПОКАЗАТЕЛИ. Пусть проект реализуется в течение только одного первого года и обеспечивает получение эффекта либо 100, либо 300 единиц с равными вероятностями. Естественно считать, что ожидаемый эффект такого проекта составит 200 единиц, однако такой эффект не отвечает ни одному из двух возможных сценариев проекта.

 

С другой стороны, разброс возможных значений эффекта (в данном примере 300 - 100 = 200) дает определенную информацию о связанном с проектом риске. Аналогичного показателя в детерминированном случае просто не существует. Итак, принципиальным отличием недетерминированной ситуации является необходимость использования новых критериальных и оценочных показателей.

 

ПОЧЕМУ ПРОИСХОДИТ ИЗМЕНЕНИЕ СОДЕРЖАНИЯ ПОНЯТИЯ ЭФФЕКТИВНОСТИ?

 

ИЗМЕНЕНИЕ СОДЕРЖАНИЯ ПОНЯТИЯ ЭФФЕКТИВНОСТИ. Пусть мы определили показатель NPV проекта, и он оказался, например, положительным. В детерминированном случае его положительность означала бы, что участие в реализации такого проекта обеспечит больший эффект, чем альтернативные направления использования средств. В ситуации неопределенности положительный NPV не гарантирует от потерь и убытков.

 

ПОЧЕМУ ПРОИСХОДИТ ИЗМЕНЕНИЕ СОДЕРЖАНИЯ ПРОЕКТА?

 

ИЗМЕНЕНИЕ СОДЕРЖАНИЯ ПРОЕКТА. В детерминированном случае затраты и результаты проекта однозначно определяются предусмотренными в нем действиями. При этом подразумевается, что все они будут выполняться точно в срок (проект превращается в план-расписание). В то же время учет факторов неопределенности допускает возможность того, что некоторые из запланированных мероприятий выполняться не будут или будут выполняться иначе и в иное время, а некоторые, хотя и будут выполнены своевременно и точно, не дадут желаемых результатов. В такой ситуации значительно возрастает роль задачи формирования организационно-экономического механизма реализации проекта. Данный механизм должен обеспечить адаптацию проекта к меняющимся условиям, корректировку хода реализации проекта в зависимости от получаемой информации. При этом содержание проекта будет трансформироваться. Здесь надо иметь определенную «стратегию», некоторый набор инструкций, определяющих, как нужно поступать участникам проекта в тех или иных ситуациях, которые могут возникнуть в процессе осуществления проекта. Это ведет к превращению проекта из «плана-расписания» в «план-инструкцию», определяющую поведение участников не только в «штатных», но и в «нештатных» ситуациях. В проектных материалах необходимо описать, причем достаточно конкретно, ликвидационные процедуры, которые в момент прекращения проекта должны обеспечить наиболее эффективную ликвидацию предприятия, наиболее полное удовлетворение требований всех участников проекта и контрагентов.

 

ПОЧЕМУ ВОЗНИКАЕТ НЕОБХОДИМОСТЬ ВВЕДЕНИЯ ДОПОЛНИТЕЛЬНЫХ ПОКАЗАТЕЛЕЙ НЕОПРЕДЕЛЕННОСТИ И РИСКА?

 

ДОПОЛНИТЕЛЬНЫЕ ПОКАЗАТЕЛИ НЕОПРЕДЕЛЕННОСТИ И РИСКА. В условиях неопределенности эффект проекта может быть большим, но может оказаться и малым, возможно, даже отрицательным. К тому же каждый экономический субъект по-своему оценивает те или иные колебания доходов и расходов. Это требует введения в рассмотрение специальных показателей, характеризующих нестабильность затрат и результатов проекта, разброс возможных значений эффекта.

 

КЛАССИФИКАЦИЯ ПРОЕКТНЫХ РИСКОВ.

 

Риск является весьма сложной и многоаспектной категорией. Не случайно в научной литературе приводятся десятки видов риска, при этом классификационным признаком чаще всего служит объект, рисковость которого пытаются охарактеризовать и проанализировать.

 

Различные подходы к классификации в большинстве случаев можно объяснить различием целей и задач классификации. Однако в ряде случаев, даже при наличии одинаковых классификационных признаков, предлагаются разные, иногда противоречивые критерии отнесения рисков к той или иной группе. В таких случаях аналитику следует руководствоваться здравым смыслом и собственным пониманием проблемы.

 

КАК КЛАССИФИЦИРУЮТСЯ ПРОЕКТНЫЕ РИСКИ ПО ИСТОЧНИКУ ВОЗНИКНОВЕНИЯ?

 

С точки зрения источника возникновения риски делятся на:

 

-  СИСТЕМАТИЧЕСКИЕ (макроэкономические) и

 

- НЕСИСТЕМАТИЧЕСКИЕ (микроэкономические).

КАКИЕ ВИДЫ РИСКОВ ВКЛЮЧАЮТ СИСТЕМАТИЧЕСКИЕ РИСКИ ?

 

Систематические риски определяются внешними обстоятельствами, не зависят от субъекта и обычно не регулируются им. К ним относятся:

 

- страновый риск;

 

- риск форс-мажорных обстоятельств.

ЧТО ТАКОЕ РИСК ФОРС-МАЖОРНЫХ ОБСТОЯТЕЛЬСТВ?

 

Риск форс-мажорных обстоятельств определяет опасность воздействия на ход реализации проекта природных катаклизмов (землетрясений, наводнений, засух и т. п.). Методы оценки этого риска на лекции мы не рассматриваем.

 

Страновый риск непосредственно связан с интернационализацией бизнеса. Он актуален для всех участников внешнеэкономической деятельности и зависит от политико-экономической стабильности стран.

 

КАК КЛАССИФИЦИРУЕТСЯ СТРАНОВОЙ РИСК?

 

Данный риск подразделяется на

 

- ЭКОНОМИЧЕСКИЙ  РИСК и  

 

- ПОЛИТИЧЕСКИЙ РИСК.

ЧЕМ МОЖЕТ БЫТЬ ВЫЗВАН ЭКОНОМИЧЕСКИЙ РИСК?

 

Экономический риск может быть вызван возможностью значительных неблагоприятных изменений в экономической сфере страны. Основными факторами экономического риска, учитываемыми иностранными инвесторами при желании работать в определенной стране, являются:

 

- масштабы экономики;

 

- реальные темпы экономического роста;

 

- ставки налогообложения;

 

- уровень инфляции;

 

- внешний долг;

 

- платежный баланс;

 

- ставка рефинансирования;

 

- доход на душу населения и др.

 

С ЧЕМ СВЯЗАН ПОЛИТИЧЕСКИЙ РИСК?

 

Политический риск, как правило, связан с последствиями изменения политической ситуации в стране.

 

КАК КЛАССИФИЦИРУЮТСЯ ПОЛИТИЧЕСКИЕ РИСКИ?

 

К политическим рискам относят:

 

- возможность политических потрясений;

 

- неясность и непредсказуемость экономической политики государства;

 

- возможность неблагоприятных изменений в законодательстве;

 

- геополитические риски;

 

- социальные риски и др.

 

Очевидно, что данные риски являются тесно коррелированными и должны рассматриваться во взаимосвязи (как единый страновый риск).

 

КАКИЕ РИСКИ ОТНОСЯТСЯ К НЕСИСТЕМАТИЧЕСКИМ РИСКАМ?

 

Несистематические риски присущи конкретному субъекту, зависят от его состояния и определяются его конкретной спецификой. Этими рисками можно и нужно управлять. Остановимся на важнейших из них.

 

ДЕЛОВОЙ РИСК — риск, определяемый отраслевой спецификой компании, осуществляющей проект, или самого проекта.

 

РИСК ФИНАНСИРОВАНИЯ — риск отсутствия необходимых денежных средств на момент осуществления проекта, а также риск изменения условий кредитования или прямого инвестирования.

 

ТЕХНИЧЕСКИЙ РИСК — риск, вызванный ошибками в проектировании, недостатками выбранной технологии, нехваткой квалифицированной рабочей силы, срывом сроков производимых работ, повышением цен на сырье, энергию и комплектующие и т. д.

МАРКЕТИНГОВЫЙ РИСК — риск низкого уровня исследования рынка.

 

РИСК «СЛАБОГО» УПРАВЛЕНИЯ.

 

РИСК ЛИКВИДНОСТИ — риск, связанный с неспособностью быстро продать активы без существенной потери в цене (возникает при необходимости продажи объекта инвестирования).

Очевидно, что вышеперечисленные риски находятся во взаимосвязи, изменения в одном из них вызывают изменения в другом, что влияет на результаты проектной деятельности. Все это обусловливает необходимость и важность учета и анализа рисков.

 

Следующим классификационным признаком является степень наносимого ущерба.

 

КАК КЛАССИФИЦИРУЮТСЯ РИСКИ ПО СТЕПЕНИ НАНОСИМОГО УЩЕРБА?

 

В соответствии с ним проектные риски разделяют на:

 

- ЧАСТИЧНЫЕ — когда запланированные показатели, действия, результаты выполнены частично, но без потерь;

 

- ДОПУСТИМЫЕ — когда запланированные показатели, действия, результаты не выполнены, но потерь нет;

 

- КРИТИЧЕСКИЕ — когда запланированные показатели, действия, результаты не выполнены, есть определенные потери;

 

- КАТАСТРОФИЧЕСКИЕ — когда невыполнение запланированного результата влечет за собой разрушение субъекта (проекта, предприятия).

КАК КЛАССИФИЦИРУЮТСЯ РИСКИ ПО ВРЕМЕНИ ВОЗНИКНОВЕНИЯ?

 

По времени возникновения риски распределяются на

 

- РЕТРОСПЕКТИВНЫЕ,

 

- ТЕКУЩИЕ и

 

- ПЕРСПЕКТИВНЫЕ.

Анализ ретроспективных рисков,  их характера и способов снижения дает возможность более точно прогнозировать текущие и перспективные риски.

 

РАЗДЕЛ 2. ПОДХОДЫ К ОЦЕНКЕ РИСКОВ ИНВЕСТИЦИОННОГО ПРОЕКТА.

 

В процессе анализа инвестиционного проекта классификационные признаки могут быть расширены и конкретизированы в соответствии с целями и задачами исследования.

 

КАКОВЫ ЭТАПЫ ПРОЦЕССА ОЦЕНКИ РИСКА?

 

Общая последовательность оценки рисков типична и включает в себя следующие действия:

 

1. Выявление источников и причин риска, этапов и работ, при выполнении которых возникает риск.

 

2. Идентификацию всех возможных рисков, свойственных рассматриваемому проекту.

 

3. Оценку уровня отдельных рисков и риска проекта в целом, определяющую его экономическую целесообразность.

 

4. Определение допустимого уровня риска.

 

5. Разработку мероприятий по снижению риска.

 

В соответствии с данным алгоритмом оценка риска подразделяется на два взаимно дополняющих направления: качественный подход (этапы 1, 2, 5) и количественный подход (этапы 3,4).

 

КАЧЕСТВЕННЫЙ ПОДХОД К ОЦЕНКЕ РИСКОВ ИНВЕСТИЦИОННОГО ПРОЕКТА.

 

Методика качественной оценки рисков проекта внешне представляется очень простой — описательной, но по существу она должна привести аналитика-исследователя к количественному результату, к стоимостной оценке выявленных рисков, их негативных последствий и «стабилизационных» мероприятий. Таким образом, главная задача качественного подхода — с помощью приведенных ниже классификаций выявить и идентифицировать возможные виды рисков, свойственных проекту; также определяются и описываются причины и факторы, влияющие на уровень данного вида риска. Кроме того, необходимо описать и дать стоимостную оценку всех возможных последствий гипотетической реализации выявленных рисков и предложить мероприятия по минимизации и/или компенсации этих последствий, рассчитав стоимостную оценку необходимых мероприятий. Результаты качественного анализа служат важной исходной информацией для осуществления количественного анализа. В основе этапов 1 и 2 процесса оценки рисков лежит определение источников и причин риска, идентификация всех возможных рисков, свойственных рассматриваемому проекту. Данная часть анализа может быть выполнена с учетом конкретной ситуации и с применением и анализом общей классификации рисков, представленной в первом разделе этой лекции.

 

Рассмотрим этап 5, касающийся разработки мероприятий по снижению риска. Важно правильно выбрать способы, позволяющие снизить проектный риск. Прежде всего, к их числу следует отнести диверсификацию, например размывание, распределение усилий предприятия между видами деятельности, результаты которых непосредственно не связаны между собой.

 

КАКИЕ ПРОЕКТНЫЕ РИСКИ МОЖНО СНИЗИТЬ С ПОМОЩЬЮ ДИВЕРСИФИКАЦИИ?

 

Любое инвестиционное решение, связанное с конкретным проектом, требует от лица, принимающего это решение, рассмотрения проекта во взаимосвязи с другими проектами и с уже имеющимися видами деятельности предприятия. Для снижения риска желательно планировать производство таких товаров или услуг, спрос на которые изменяется в противоположных направлениях. Однако следует помнить, что диверсификация является способом снижения несистематического риска. СИСТЕМАТИЧЕСКИЙ РИСК ПОСРЕДСТВОМ ДИВЕРСИФИКАЦИИ НЕВОЗМОЖНО СОКРАТИТЬ.

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ СНИЖЕНИЕ ПРОЕКТНОГО РИСКА ПОСРЕДСТВОМ РАСПРЕДЕЛЕНИЯ ЕГО МЕЖДУ УЧАСТНИКАМИ ИНВЕСТИЦИОННОГО ПРОЕКТА?

 

Распределение проектного риска между участниками проекта является эффективным способом его снижения. Логичнее всего при этом сделать ответственным за конкретный вид риска того из его участников, который обладает возможностью точнее и качественнее рассчитывать и контролировать данный риск. Это распределение оформляется при разработке финансового плана проекта и контрактных документов.

 

В ЧЕМ СУЩНОСТЬ СТРАХОВАНИЯ КАК СПОСОБА СНИЖЕНИЯ ПРОЕКТНОГО РИСКА?

 

Наиболее распространенным способом снижения риска является его страхование, которое состоит, по существу, в передаче определенных рисков страховой компании. Зарубежная практика страхования использует полное страхование инвестиционных проектов. Условия российской действительности позволяют пока только частично страховать риски проекта: здания, оборудование, персонал, ущерб от некоторых экстремальных ситуаций и т. д.

 

КАКУЮ РОЛЬ ИГРАЕТ ПРИОБРЕТЕНИЕ ДОПОЛНИТЕЛЬНОЙ ИНФОРМАЦИИ ДЛЯ СНИЖЕНИЯ ПРОЕКТНЫХ РИСКОВ?

 

Важную роль в снижении рисков инвестиционного проекта играет приобретение дополнительной информации. Цель такого приобретения — уточнение некоторых параметров проекта, повышение уровня надежности и достоверности исходной информации, что позволит снизить вероятность принятия неэффективного решения. Способы получения дополнительной информации включают ее приобретение у других организаций (предприятий, научно-исследовательских и проектных организаций, консалтинговых фирм и т. п.), проведение дополнительного эксперимента и т. д.

 

КАКУЮ РОЛЬ ИГРАЕТ РЕЗЕРВИРОВАНИЕ СРЕДСТВ НА ПОКРЫТИЕ НЕПРЕДВИДЕННЫХ РАСХОДОВ ДЛЯ СНИЖЕНИЯ ПРОЕКТНЫХ РИСКОВ?

 

Резервирование средств на покрытие непредвиденных расходов также является одним из наиболее распространенных способов снижения риска инвестиционного проекта. Зарубежный опыт допускает увеличение стоимости проекта от 7 до 12% за счет резервирования средств на форс-мажор. Резервирование средств предусматривает установление соотношения между потенциальными рисками, изменяющими стоимость проекта, и размером расходов, связанных с преодолением нарушений в ходе его реализации.

 

В ЧЕМ СОСТОЯТ ОСНОВНЫЕ РЕЗУЛЬТАТЫ КАЧЕСТВЕННОГО АНАЛИЗА ПРОЕКТНЫХ РИСКОВ?

 

Итак, основными результатами качественного анализа рисков являются:

 

- выявление конкретных рисков проекта и порождающих их причин,

 

- анализ и стоимостный эквивалент гипотетических последствий возможной реализации отмеченных рисков,

 

- предложение мероприятий по минимизации ущерба и, наконец, их стоимостная оценка.

 

К дополнительным, но также весьма значимым, результатам качественного анализа следует отнести определение пограничных значений возможного изменения всех факторов (переменных) проекта, проверяемых на риск.

 

КОЛИЧЕСТВЕННЫЙ ПОДХОД К АНАЛИЗУ ПРОЕКТНЫХ РИСКОВ.

 

Количественный подход к анализу проектных рисков базируется на информации, полученной в ходе качественного анализа, и предполагает численное определение отдельных рисков и риска проекта (решения) в целом. На данном этапе определяются численные значения вероятности наступления рисковых событий и их последствий, осуществляется количественная оценка степени (уровня) риска, определяется допустимый в данной конкретной обстановке уровень риска.

 

В исследованиях, посвященных проблеме риска, встречается много различных методов количественной оценки риска.

 

КАКИЕ МЕТОДЫ КОЛИЧЕСТВЕННОГО АНАЛИЗА ПРОЕКТНЫХ РИСКОВ МОЖНО ВЫДЕЛИТЬ?

 

Наиболее часто встречающимися методами количественного анализа рисков проекта являются:

 

- СТАТИСТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ;

 

- МЕТОД ЭКСПЕРТНЫХ ОЦЕНОК;

 

- МЕТОД АНАЛОГИЙ;

 

- ГРУППА АНАЛИТИЧЕСКИХ МЕТОДОВ.

КАКИМ ОБРАЗОМ ОЦЕНИВАЮТСЯ РИСКИ С ПОМОЩЬЮ СТАТИСТИЧЕСКИХ МЕТОДОВ?

 

Основной задачей статистических методов оценки рисков является определение вероятности наступления отдельного неблагоприятного события на основе статистического исследования имеющихся данных о деятельности конкретного рискового объекта (организации) в прошлом. В наиболее простом случае количественно частные риски деятельности оцениваются с использованием показателей дисперсии, среднеквадратического отклонения, коэффициента вариации, а результаты их влияния — на основании средних ожидаемых значений исследуемых показателей (указанные критерии оценки мы рассмотрим в разделе 3 лекции «Измерение и количественная оценка риска»). В зависимости от глубины анализа возможны исследование и оценка отдельных неблагоприятных событий, но более корректным является представление о неблагоприятном событии как об интегральной (многопараметрической) величине, определенной на основе частных рисков.

 

Статистические методы количественной оценки риска являются одними из наиболее распространенных методов. К их преимуществам следует отнести несложность математических расчетов, а к недостаткам — необходимость большого числа наблюдений (чем больше массив данных, тем достовернее оценка рисков).

 

В ЧЕМ СОСТОИТ ПРЕИМУЩЕСТВО МЕТОДА ЭКСПЕРТНЫХ ОЦЕНОК?

 

Главное преимущество метода экспертных оценок заключается в возможности использования опыта экспертов в процессе анализа проекта и учета влияния разнообразных качественных факторов.

 

В ЧЕМ ОБЫЧНО СОСТОИТ ПРОЦЕДУРА ЭКСПЕРТНОЙ ОЦЕНКИ?

 

Формально процедура экспертной оценки чаще всего состоит в следующем. Руководство проекта (фирмы) разрабатывает перечень критериев оценки в виде экспертных (опросных) листов. Для каждого критерия назначаются (реже — исчисляются) соответствующие весовые коэффициенты, которые не сообщаются экспертам. Затем по каждому критерию составляются варианты ответов, веса которых также неизвестны экспертам.

 

Эксперты, проводя экспертизу, должны обладать полной информацией об оцениваемом проекте, анализировать поставленные вопросы и отмечать выбранный вариант ответа. Далее заполненные экспертные листы обрабатываются соответствующим образом (на основании известных статистических (компьютерных) пакетов обработки информации) и выдается результат (или результаты) проведенной экспертизы.

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ ОСОБЕННОСТЬ МЕТОДА ДЕЛЬФИ КАК МЕТОДА ЭКСПЕРТНЫХ ОЦЕНОК?

 

Метод экспертной оценки рисков, описанный выше, можно дополнить его разновидностью, так называемым методом Дельфи. Он характеризуется строгой процедурой организации проведения оценки рисков, при которой эксперты лишены возможности совместно обсуждать ответы на поставленные вопросы, что позволяет избежать «ловушек» группового принятия решения и доминирования мнения лидера, обеспечить анонимность оценок. Обработанные и обобщенные результаты через управляемую обратную связь сообщаются каждому члену экспертной комиссии. Таким образом, снимается возможность психологического дискомфорта, связанного с персонификацией каждой оценки, после чего оценка может быть повторена.

 

Качество экспертной оценки проектных рисков в большой степени зависит от качества подбора экспертов, чему необходимо уделять серьезное внимание.

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ СУЩНОСТЬ МЕТОДА АНАЛОГИЙ?

 

Сущность метода аналогий состоит в анализе всех имеющихся данных об уже реализованных инвестиционных проектах, имеющих высокую степень сходства с оцениваемым. Это делается с целью расчета вероятностей возникновения потерь. Наиболее часто метод аналогий применяется при оценке риска часто повторяющихся проектов, например в строительстве.

 

Метод аналогий чаще всего используется в том случае, если другие методы оценки риска неприемлемы, и связан с использованием базы данных о рисках аналогичных проектов. Важным подспорьем при проведении анализа проектных рисков с помощью метода аналогий является оценка проектов после их завершения, практикуемая рядом известных банков, например Всемирным банком. Полученные в результате таких исследований данные обрабатываются для выявления зависимостей в законченных проектах, что позволяет выявлять потенциальный риск при реализации нового инвестиционного проекта.

 

КАКИЕ ГРУППЫ АНАЛИТИЧЕСКИХ МЕТОДОВ МОЖНО ВЫДЕЛИТЬ?

 

Весь массив аналитических методов можно разделить на две подгруппы в зависимости от привлечения вероятностных распределений:

 

- МЕТОДЫ БЕЗ УЧЕТА РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТЕЙ;

 

- МЕТОДЫ С УЧЕТОМ РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТЕЙ.

1. МЕТОДЫ БЕЗ УЧЕТА РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТЕЙ являются относительно «старыми» способами учета риска и могут быть представлены:

 

- анализом чувствительности критериев эффективности проекта;

 

- анализом сценариев;

 

- методом корректировки отдельных параметров проекта.

В ЧЕМ ЗАКЛЮЧАЕТСЯ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ КРИТЕРИЕВ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА?

 

Анализ чувствительности критериев эффективности — простейший и поэтому наиболее часто используемый количественный метод исследования рисков. С его помощью можно показать, как изменяется значение некоторого критерия эффективности (например, NPV) при изменении значения заданной переменной (фактора воздействия). С помощью данного метода может быть охарактеризована степень устойчивости проекта к возможным изменениям условий реализации и выявлены наименее и наиболее рискованные для проекта факторы.

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ АНАЛИЗ СЦЕНАРИЕВ?

 

Анализ сценариев представляет собой развитие методики анализа чувствительности проекта, поскольку он предполагает, что одновременному изменению подвергается вся группа переменных, проверяемых на риск. В результате определяется воздействие одновременного изменения всех основных переменных проекта, характеризующих его денежные потоки, на критерии проектной эффективности. Важным преимуществом этого метода является тот факт, что отклонения параметров рассчитываются с учетом их взаимозависимостей (корреляции).

 

Более подробно анализ чувствительности и анализ сценариев мы рассматриваем далее.

 

В КАКИХ СЛУЧАЯХ ПРИМЕНЯЕТСЯ МЕТОД КОРРЕКТИРОВКИ ОТДЕЛЬНЫХ ПАРАМЕТРОВ ИНВЕСТИЦИОННОГО ПРОЕКТА?

 

Возможная неопределенность условий реализации проекта может учитываться путем корректировки параметров проекта:

 

- сроки строительства и выполнения других работ увеличиваются на среднюю величину возможных задержек;

 

- учитывается среднее увеличение стоимости строительства, обусловленное ошибками проектной организации, пересмотром проектных решений в ходе строительства и непредвиденными расходами;

 

- учитывается запаздывание платежей, неритмичность поставок сырья и материалов, допускаемые персоналом нарушения технологии и т. п.;

 

- увеличивается норма дисконта.

 

Далее, в разделе 3 этой лекции, мы рассмотрим наиболее интересную корректировку -  увеличение ставки дисконта на величину надбавки за риск при расчете эффективности проекта.

 

2. Вторую группу аналитических методов представляют МЕТОДЫ ОЦЕНКИ ПРОЕКТНЫХ РИСКОВ С УЧЕТОМ РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТЕЙ. Они предполагают, что построение и расчеты по модели осуществляются в соответствии с принципами теории вероятностей.

 

В рамках этой группы методов мы отметим самые популярные на сегодняшний день, а именно:

 

- методы, основанные на использовании теории принятия решений (критерии принятия решений в условиях неопределенности, в условиях риска, с помощью «дерева решений»);

 

- метод Монте-Карло.

КАКОВЫ ИСТОЧНИКИ НЕОПРЕДЕЛЕННОСТИ В ЭКОНОМИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ?

 

Любая сфера экономической деятельности, в особенности инвестиционное планирование, связана с принятием решений в условиях неполноты информации. Источники неопределенности могут быть разные: нестабильность экономической и/или политической ситуации, неопределенность действий партнеров по бизнесу, неточность информации и множество других случайных факторов. Экономические решения с учетом всех этих факторов принимаются в рамках так называемой теории принятия решений — аналитического подхода к выбору наилучшего действия или последовательности действий.

 

КАКИЕ МАТЕМАТИЧЕСКИЕ  МОДЕЛИ РАССМАТРИВАЮТСЯ В ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ?

 

В теории решений принято отличать ситуацию риска от ситуации неопределенности. В соответствии с этим в теории принятия решений выделяются два типа моделей, которые требуют разных подходов к выбору оптимальных решений и используют различные критерии.

 

Имитационное моделирование по методу Монте-Карло (Monte-Carlo Simulation) позволяет построить математическую модель для проекта с неопределенными значениями параметров и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию), получить распределение доходности проекта.

 

Данный метод является наиболее сложным, но и наиболее корректным методом учета и оценки рисков при принятии инвестиционного проекта, поскольку наиболее полно характеризует всю гамму неопределенностей, с которой может столкнуться реальный инвестиционный проект, и через задаваемые изначально ограничения позволяет учитывать всю доступную проектному аналитику информацию. Практическая реализация данного метода возможна только с применением компьютерных программ, позволяющих описывать прогнозные модели и рассчитывать большое число случайных сценариев.

 

Мы осуществили краткий обзор наиболее используемых методов учета факторов риска и неопределенности в инвестиционном проектировании. Перейдем к их более детальному рассмотрению в соответствии с предложенной классификацией.

 

РАЗДЕЛ 3.  ИЗМЕРЕНИЕ И КОЛИЧЕСТВЕННАЯ ОЦЕНКА РИСКА.

 

КАК МОЖНО ИЗМЕРИТЬ И ОЦЕНИТЬ РИСК?

 

Риск — категория вероятностная, поэтому в процессе оценки неопределенности и количественного определения степени риска используют вероятностные расчеты.

 

КАКОВЫ СТАНДАРТНЫЕ ХАРАКТЕРИСТИКИ РИСКА?

 

С использованием основных понятий теории вероятностей рассчитывают стандартные характеристики риска. Рассмотрим основные характеристики.

 

Прежде всего, напомним определение случайной величины.

 

ЧТО НАЗЫВАЕТСЯ СЛУЧАЙНОЙ ВЕЛИЧИНОЙ?

 

Величину называют случайной, если в результате испытания она примет лишь одно возможное значение, заранее не известное и зависящее от случайных причин.  Каждой случайной величине соответствует множество чисел (множество значений, которые она может принимать).

 

КАКИЕ ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН СУЩЕСТВУЮТ?

 

Различают два вида случайных величин.  

 

Случайная величина, принимающая отдельные возможные значения (числа) с определенными вероятностями, называется  ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНОЙ.

НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНОЙ называется случайная величина, которая может принимать все значения из некоторого числового промежутка.

Для задания дискретной случайной величины нужно задать не только перечень ее возможных значений, но и их вероятности. Иными словами, каждому возможному значению случайной величины соответствует определенное значение вероятности появления этого значения случайной величины. 

 

ЧТО ТАКОЕ ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

 Соответствие между отдельными возможными значениями и их вероятностями называется ЗАКОНОМ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. 

 

Как и в случае функциональной зависимости, этот закон можно задать таблицей, аналитически (формулой) и графически.

 

В случае табличного задания закона распределения дискретной случайной величины соответствующая таблица состоит из двух строк: в первой строке указаны возможные значения, а во второй строке в соответствующих столбцах под возможными значениями указаны вероятности этих значений. То есть имеем следующую таблицу.

 

Таблица 1.

X	x1	x2	…	xn
P	p1	p2	…	pn

Поскольку в одном испытании случайная величина принимает только одно возможное значение, то события Х=х₁, Х=х₂, ..., Х=х_n образуют полную группу, т.е. сумма их вероятностей равна единице: 

 

p₁+ p₂+ … + p_n = 1.  

 

Если множество возможных значений Х дискретной случайной величины бесконечно, то соответствующий ряд вероятностей сходится и его сумма равна единице:

 

p₁+ p₂+ … + p_n + … = 1.

 

ЧТО ТАКОЕ МНОГОУГОЛЬНИК РАСПРЕДЕЛЕНИЯ  ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

Закон распределения дискретной случайной величины можно изобразить графически, соединив в прямоугольной системе координат XOY точки (х_i; p_i) отрезками прямых. Такая фигура называется многоугольником распределения (рисунок 1).

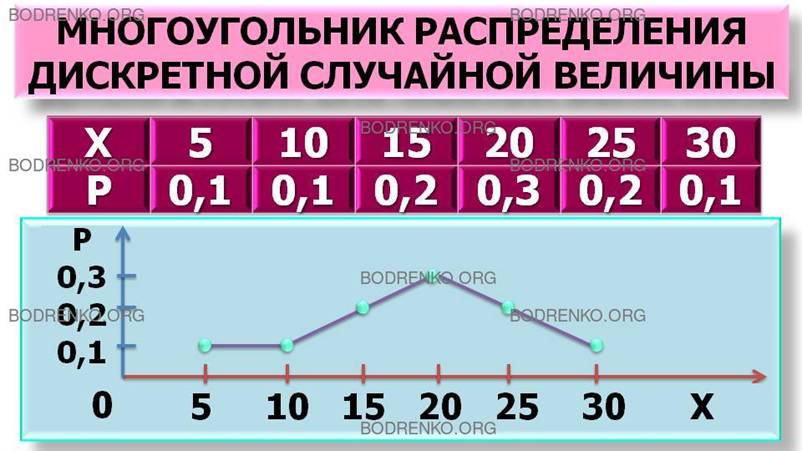
Рисунок 1. Многоугольник распределения дискретной случайной величины.

 

Рассмотрим основные числовые характеристики  дискретных случайных величин.

 

Установленный закон распределения полностью характеризует случайную величину. Однако часто используются числовые характеристики случайной величины, которые дают некоторое осредненное описание случайной величины, получаемое на базе закона ее распределения.

 

1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

КАК ОПРЕДЕЛЯЕТСЯ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ  ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

Пусть случайная величина Х может принимать значения x₁, x₂, …, x_n  с вероятностями соответственно p₁, p₂, …, p_n.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности:

М(Х) =x₁∙р₁+x₂∙р₂+ … + x_n∙p_n .    (1)

Из этого определения следует, что математическое ожидание есть некоторая постоянная (неслучайная) величина. Вероятностный же смысл математического ожидания состоит в том, что оно приближенно равно (в особенности для большого числа испытаний) среднему арифметическому значению случайной величины.  Таким образом, математическое ожидание представляет собой обобщенную количественную характеристику ожидаемого результата.

 

2. ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

Как мы уже отметили, математическое ожидание является средней характеристикой случайной величины. Однако оно не характеризует случайную величину достаточно полно, и по этой причине рассматриваются и другие числовые характеристики. Пусть Х — случайная величина, а М(Х) — ее математическое ожидание.  

 

ЧТО ТАКОЕ ОТКЛОНЕНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

 Разность между случайной величиной X и ее математическим ожиданием M(X) называется отклонением.

 
Пусть закон распределения случайной величины Х дается таблицей 1, тогда отклонение (Х – М(Х)) имеет следующий закон распределения.

 

 

X – M(X)	x1 – M(X)	x2 – M(X)	…	xn – M(X)
P	p1	p2	…	pn

ЧТО ТАКОЕ ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 

На практике важной характеристикой является рассеяние возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения равно нулю. Так как при непосредственном вычислении математического ожидания отклонения в общем случае суммируются отрицательные и положительные отклонения, умноженные на соответствующие вероятности, то целесообразно ввести в рассмотрение абсолютные значения отклонений или их квадраты.

Математическое ожидание квадрата отклонения называется дисперсией (или рассеянием) случайной величины X:  

 

D(Х)=М[Х – М(Х)]². (2)  

Пусть дискретная случайная величина X задана законом распределения (таблица 1), тогда квадрат отклонения этой случайной величины имеет следующий закон распределения:

 

[X – M(X)]2	[x1 – M(X)]2	[x2 – M(X)]2	…	[xn – M(X)]2
P	p1	p2	…	pn

 

Отсюда, согласно формуле (2), получаем формулу для вычисления дисперсии в развернутом виде:

 

D(Х) =p₁∙[x₁ – M(Х)]² + p₂∙[x₂ – M(Х)]² + … + p_n∙[x_n – M(Х)]² .

При вычислении дисперсии часто бывает удобно воспользоваться формулой, которая непосредственно выводится из формулы (2):

 

D(Х)=М(Х²) — [М(Х)]². (3)

3. СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. 

 

Одной из основных оценок рассеяния возможных значений случайной величины служит среднеквадратическое отклонение.

 

КАК ОПРЕДЕЛЯЕТСЯ СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

Среднеквадратическим отклонением случайной величины Х (стандартом) называется квадратный корень из ее дисперсии:

 

σ(Х)=√D(X) . (4)

Среднеквадратическое отклонение показывает степень разброса возможных результатов по проекту и, следовательно, степень риска; при этом более рискованные инвестиции дают большее значение данной величины. Среднеквадратическое отклонение является абсолютной мерой риска и измеряется в тех же физических единицах, в каких измеряется варьирующий признак.

 

4. КОЭФФИЦИЕНТ ВАРИАЦИИ. Для анализа меры изменчивости часто используют коэффициент вариации (V), который представляет собой отношение среднеквадратического отклонения к математическому ожиданию. Коэффициент вариации вычисляется по формуле:

 

V(X)=σ(X)/M(X).  (5)

Коэффициент вариации — относительная величина. Поэтому с его помощью можно сравнивать колеблемость признаков, выраженных в различных единицах измерения.

 

5. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

 

Пусть Х — непрерывная случайная величина, значения которой сплошь заполняют числовой интервал (a, b). Теперь уже нельзя составить перечень всех возможных значений Х, так это было сделано в случае дискретной случайной величины. Тем не менее, существует способ задания любых видов случайных величия.

 

Пусть х — действительное число. Обозначим вероятность события того, что Х примет значение, меньшее х, через F(х).

 

ЧТО НАЗЫВАЕТСЯ ФУНКЦИЕЙ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ?

 
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что Х примет значение, меньшее х:

 

F(х)= Р(Х<х). (6)

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ F(Х)?

 

F(x) – это вероятность того, что случайная величина Х примет значение, которое изображается точкой на числовой оси, расположенной левее точки х.  

 

По виду функции F(х) определяется и вид случайной величины.

6. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ.

 

ЧТО ТАКОЕ ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ?

 

Производная от функции распределения непрерывной случайной величины Х называется плотностью распределения вероятностей Х:

 

f(x)=F`(х). (7)

 

Из этого определения следует, что функция распределения является первообразной для плотности распределения или неопределенным интегралом от нее.

 

Плотность распределения – это скорость изменения вероятности Р(Х<х).

 

Связь между функцией распределения и плотностью распределения вероятностей устанавливается, согласно определению плотности распределения вероятностей (7), формулой

 

                      x

F(х)=P(Х<х) = ∫f(x) dx. (8)
                       -∞

Из формулы (8) следует справедливость следующей фундаментальной  теоремы.
 

ТЕОРЕМА. Вероятность того, что непрерывная случайная  величина Х примет значение на интервале (α, β), определяется по формуле

                  

        β
Р(α<Х<β) = ∫ f(t) dt. (9)

                  α

Вспоминая геометрический смысл определенного интеграла, можно сказать, что вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (α, β), равна площади криволинейной трапеции, ограниченной сверху кривой плотности распределения f(х), снизу – осью Оx, а с краев — вертикальными прямыми х =α‚ и х=β (рисунок 2).

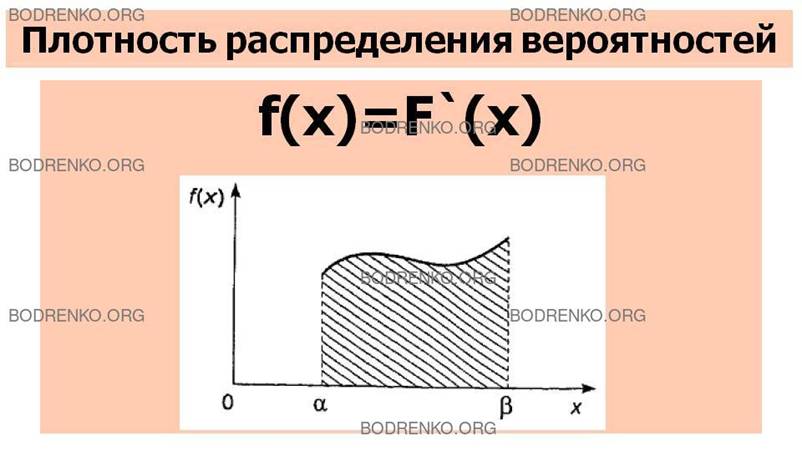
Рисунок 2. График функции f(x) плотности распределения вероятностей.

 

 

КАК ОПРЕДЕЛЯЮТСЯ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН?

 

Определения числовых характеристик дискретных случайных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (1) и (2) берутся их интегральные аналоги. 

 

Характер, тип распределения отражает общие условия, вытекающие из сущности и природы явления, и особенности, оказывающие влияние на вариацию исследуемого показателя (ожидаемого результата). Как показывает практика, для характеристики распределения социально-экономических явлений наиболее часто используется так называемое нормальное распределение.

 

КАКОЕ  РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НАЗЫВАЕТСЯ НОРМАЛЬНЫМ?  

 

Общим нормальным распределением вероятностей непрерывной случайной величины Х называется распределение с плотностью

f(х)=(1/(σ∙√(2π)))∙exp{-(x - a)²/(2∙σ²)}      . (10)

Нормальное распределение задается двумя параметрами: a и σ.

Согласно определениям математического ожидания и дисперсии, после выполнения соответствующих интегрирований можно вывести, что для нормального распределения справедливы следующие формулы.

М(Х)=a,

D(Х)=σ²,

σ(Х)=σ.

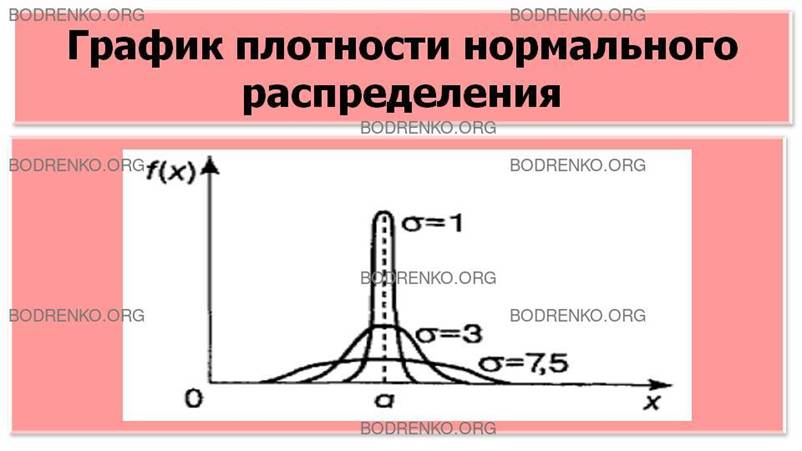
График функции f(X) для нормального распределения представляет собой, так называемую нормальную кривую (кривую Гаусса) (рисунок 3).

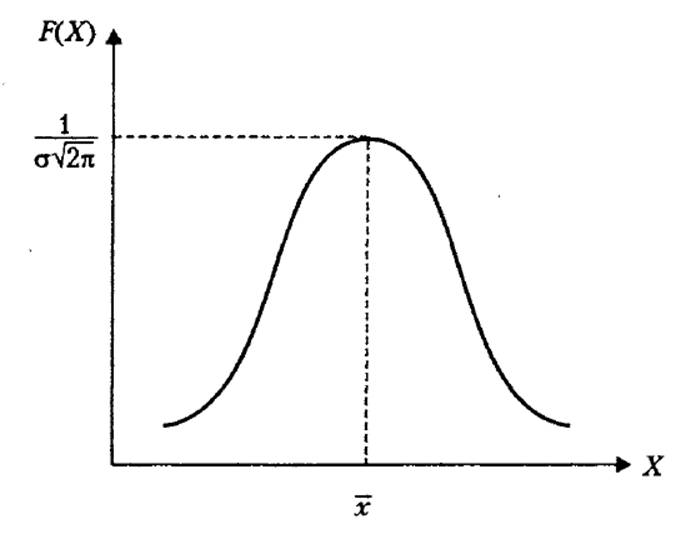
Рисунок 3. График плотности нормального распределения.

 

 

7. СТАТИСТИЧЕСКАЯ ЗАВИСИМОСТЬ МЕЖДУ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ.

 

Случайные величины X и Y подвержены действию различных случайных факторов, среди которых могут быть факторы, общие для двух случайных величин.

 

ПРИМЕР. Например, если на случайную величину X действуют факторы Z₁, Z₂, ..., V₁, V₂, а на случайную величину Y действуют факторы Z₀, Z₂, V₁, V₃..., то наличие двух общих факторов Z₂ и V₁ позволит говорить о вероятностной или статистической зависимости между случайными величинами X и Y.

 

ЧТО ТАКОЕ СТАТИСТИЧЕСКАЯ ЗАВИСИМОСТЬ МЕЖДУ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ?

 

Статистической называется зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины.

 

В ЧЕМ, В ЧАСТНОСТИ, МОЖЕТ ПРОЯВЛЯТЬСЯ СТАТИСТИЧЕСКАЯ ЗАВИСИМОСТЬ?

 

В частном случае статистическая зависимость проявляется в том, что при изменении одной из величин изменяется математическое ожидание другой. В этом случае говорят о корреляции или корреляционной зависимости. Статистическая зависимость проявляется только в массовом процессе, при большом числе единиц совокупности. При стохастической закономерности для заданных значений зависимой переменной можно указать ряд значений объясняющей переменной, случайно рассеянных в интервале. Каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это обусловливается тем, что зависимая переменная, кроме выделенной переменной, подвержена влиянию ряда неконтролируемых или неучтенных факторов. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.

 

Установление зависимости между двумя или более наблюдаемыми величинами является одним из важных приложений методов математической статистики. При этом наряду с раздельным анализом выборок, составленных из значений этих величин, возможен и их совместный анализ.  Наряду с анализом случайных величин X и Y по отдельности представляет интерес исследование возможной зависимости между ними. Являются ли величины X и Y независимыми? Если же между ними имеется некоторая зависимость, то какова она?

 

ЧТО ТАКОЕ КОРРЕЛЯЦИЯ?

 

КОРРЕЛЯЦИЯ (лат. correlatio - соотношение) – это понятие, указывающее на статистическую зависимость, существующую между изучаемыми явлениями.

 

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ. Коэффициент корреляции (R) показывает связь между переменными, состоящую в изменении средней величины одной из них в зависимости от изменения другой.

 

В КАКИХ СЛУЧАЯХ ИСПОЛЬЗУЕТСЯ КОЭФФИЦИЕНТ ЛИНЕЙНОЙ КОРРЕЛЯЦИИ ПИРСОНА?

 

Коэффициент линейной корреляции Пирсона используется для оценки тесноты (силы) связи между двумя переменными в случаях, если: 1) рассматриваемая связь линейная; 2) обе переменные измерены в сильных шкалах (шкале отношений или интервальной шкале).

 

Если зависимость близка к линейной, то есть  точки заметным образом группируются вокруг некоторой прямой, то в таких случаях говорят о линейной корреляции величин X и Y. В этом случае определение степени коррелированности случайных величин основано на вычислении коэффициента корреляции R_xy.  Коэффициент корреляции обладает следующим свойством:

 

-1≤R_xy≤+1.

 

При этом,  чем ближе R_xy к нулю, тем слабее корреляция. И наоборот, чем ближе коэффициент корреляции R_xy  к (+1) или (-1), тем сильнее корреляция, т. е. зависимость между случайными величинами X и Y близка к линейной. Если значение R_xy в точности равно (+1) или (- 1), то связь между X и Y линейная.

 

Коэффициент корреляции вычисляется по формуле:

 

 

 

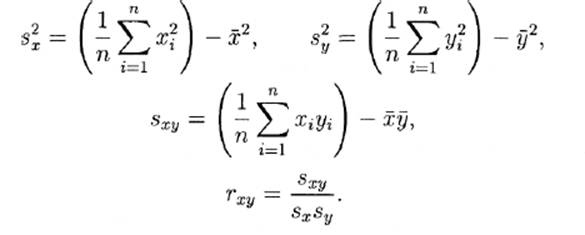
Поскольку на формирование ожидаемого результата воздействует множество случайных факторов, то он естественно является случайной величиной. Изложенные выше показатели являются исходной базой, применяемой для количественной оценки риска с применением, как статистических методов, так и других подходов, использующих теорию вероятностей.

 

МЕТОДЫ ОЦЕНКИ РИСКОВ БЕЗ УЧЕТА РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТЕЙ.

 

АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ.

 

В ходе анализа чувствительности (уязвимости) происходит последовательно-единичное изменение всех проверяемых на рискованность переменных: каждый раз, как только одна из переменных меняет свое значение на прогнозное число процентов, и на этой основе пересчитывается новая величина принятого критерия.

 

КАК ПРОВОДИТСЯ АНАЛИЗ БЕЗУБЫТОЧНОСТИ?

 

В международной практике широко используется анализ точки безубыточности (break even point analysis), который является простейшим способом, позволяющим проводить грубую оценку рисков проекта, и одним из элементов финансовой информации, используемой при оценке эффективности инвестиционных проектов.

 

Анализом безубыточности называется исследование взаимосвязи объема производства, себестоимости и прибыли при изменении этих показателей в процессе производства. Цель такого анализа — выявление сбалансированного соотношения между издержками, объемом производства и прибылями; в конечном счете — нахождение объема реализации, необходимого для возмещения издержек.

 

Проведение анализа безубыточности представляет собой моделирование реального процесса и базируется на следующих исходных предпосылках.

 

1. Неизменность цен реализации, с одной стороны, и цен на потребляемые производственные ресурсы — с другой.

 

2. Разделение затрат предприятия на постоянные, которые остаются неизменными при незначительных изменениях объема производства, и переменные, изменение которых предполагается пропорциональным объему.

 

3. Пропорциональность поступающей выручки и объема реализации.

 

4. Существование единственной точки критического объема производства (что вытекает из вышеперечисленных условий).

 

5. Равенство объема производства объему реализации.

 

6. Постоянство ассортимента изделий в случае выпуска нескольких изделий.

 

Как видно, описанная система предпосылок является весьма жесткой, что, естественно, не может не сказаться на точности результатов работы с моделью.

 

В КАКОЙ ФОРМЕ ПРОВОДИТСЯ АНАЛИЗ ТОЧКИ БЕЗУБЫТОЧНОСТИ?

 

Анализ точки безубыточности может иметь как графическую, так и аналитическую форму. В первом случае — это график взаимосвязи между названными показателями (см.: рисунок 2), где объем реализации, необходимый для возмещения издержек, характеризуется особой точкой — точкой критического объема производства (точкой безубыточности). При таком объеме выпуска предприятие не получает ни прибыли, ни убытка, т.е. выручка от реализации продукции равна ее полной себестоимости (издержкам).

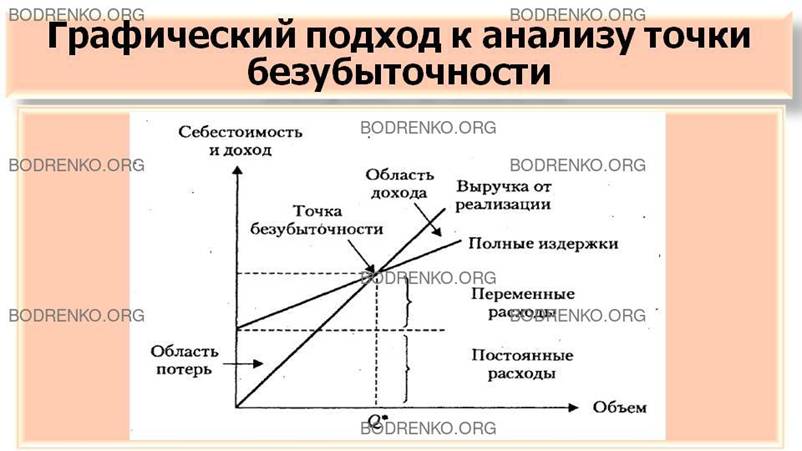
Рисунок 2. Графический подход к анализу точки безубыточности.

 

Аналитический подход предполагает выявление воздействия на прибыль изменений в объеме продаж (Q). Элементами, которые определяют соотношение между этими переменными, являются:

 

- цена единицы продукции (Р),

 

- переменные затраты на единицу продукции (AVC) и

 

- постоянные затраты (FC),

 

Общие затраты, равные сумме постоянных и переменных, составляют величину

(AVC∙Q + FC). Выручка равна величине (P∙Q). В точке безубыточности (Q*) соблюдается равенство общих затрат и выручки, т. е.

 

P∙Q* = AVC∙Q* + FC.

 

Решая данное уравнение относительно величины объема производства продукции, обеспечивающего это равенство, получим:

 

Q*=FC/(P – AVC)

 

(11)

Последовательно варьируя значения переменных в правой части этого выражения, можно проводить простейший анализ чувствительности.

 

Однако, как уже отмечалось, сильная система исходных предпосылок и различные способы расчетов как постоянных, так и переменных затрат (учет или неучет налогов, инфляции и т. д.) оказывают существенное влияние на конечный результат.

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ КЛАССИЧЕСКИЙ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ?

 

1. В ходе классического анализа чувствительности (уязвимости), применяемого к проекту, происходит последовательно-единичное изменение каждой переменной: только одна из переменных меняет свое значение на прогнозное число процентов, и на этой основе пересчитывается новая величина используемого критерия (например,  NPV или IRR). Затем оценивается процентное изменение критерия по отношению к базисному случаю и рассчитывается показатель чувствительности, представляющий собой отношение процентного изменения критерия к изменению значения переменной на один процент (так называемая эластичность изменения показателя). Таким же образом исчисляются показатели чувствительности по каждой из остальных переменных.

 

2. На следующем шаге, используя результаты проведенных расчетов, осуществляют экспертное ранжирование переменных по степени важности (например: очень высокая, средняя, невысокая) и экспертную оценку прогнозируемости (предсказуемости) значений переменных (например: высокая, средняя, низкая). Далее эксперт может построить так называемую «матрицу чувствительности», позволяющую выделить наименее и наиболее рискованные для проекта переменные (показатели).

 

Описанная методология проведения анализа чувствительности позволяет рекомендовать следующую достаточно формализованную конкретную процедуру (примерную схему) проведения анализа чувствительности инвестиционного проекта.

 

ПРИМЕР. Рассмотрим следующие условные данные (таблицы 1 -  3).

 

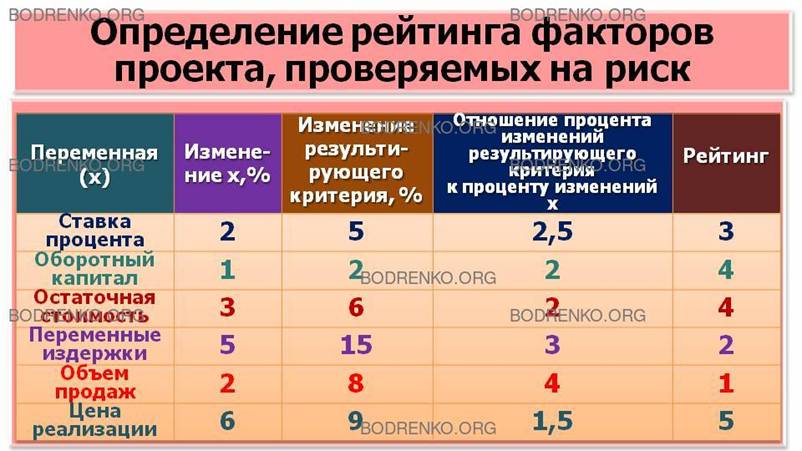
Таблица 1. Определение рейтинга факторов проекта, проверяемых на риск.

 

Переменная (х)	Изменение х,%	Изменение результирующего критерия, %	Отношение процента изменений результирующего критерия к проценту изменений x	Рейтинг
Ставка процента	2	5	2,5	3
Оборотный капитал	1	2	2	4
Остаточная стоимость	3	6	2	4
Переменные издержки	5	15	3	2
Объем продаж	2	8	4	1
Цена реализации	6	9	1,5	5

 

Таблица 2. Показатели чувствительности и прогнозируемости переменных в инвестиционном проекте.

 

Переменная (х)	Чувствительность	Возможность прогнозирования
Объем продаж	высокая	низкая
Переменные издержки	высокая	высокая
Ставка процента	средняя	средняя
Оборотный капитал	средняя	средняя
Остаточная стоимость	низкая	высокая
Цена реализации	низкая	низкая

 

КАК СТРОИТСЯ МАТРИЦА ЧУВСТВИТЕЛЬНОСТИ И ПРЕДСКАЗУЕМОСТИ?

 

На основе результатов анализа каждый фактор займет свое соответствующее место в поле матрицы чувствительности и предсказуемости. В соответствии с экспертным разбиением чувствительности и предсказуемости по их степеням матрица содержит девять элементов, которые можно распределить по зонам. Попадание фактора в определенную зону будет означать конкретную рекомендацию для принятия решения о дальнейшей работе с ним по анализу рисков.

 

Таблица 3. Матрица чувствительности и предсказуемости.

 

Чувствительность   Предсказуемость	Высокая	Средняя	Низкая
Низкая	I	I	II
Средняя	I	II	III
Высокая	II	III	III

 

Итак, первая зона (I) — левый верхний угол матрицы — зона дальнейшего анализа попавших в нее факторов, так как к их изменению наиболее чувствительна NPV проекта и они обладают наименьшей прогнозируемостью.

 

Вторая зона (II) совпадает с элементами побочной диагонали матрицы и требует пристального внимания к происходящим изменениям расположенных в ней факторов.

 

Наконец, третья зона (III), правый нижний угол таблицы, — зона наибольшего благополучия: в ней находятся факторы, которые при всех прочих предположениях и расчетах являются наименее рискованными и не подлежат дальнейшему рассмотрению.

 

В соответствии с данными таблицы 1 и таблицы 2 распределение факторов по зонам в нашем условном примере следующее.

 

1. Объем продаж необходимо подвергнуть дальнейшему исследованию на рискованность (зона I).

 

2. Внимательного наблюдения в ходе реализации проекта требуют переменные издержки, ставка процента, оборотный капитал и цена реализации (зона II).

 

3. Остаточная стоимость при сделанных экспертами-исследователями предпосылках не является для проекта рискованным фактором (зона III).

 

КАКИЕ НЕДОСТАТКИ ИМЕЕТ МЕТОД АНАЛИЗА ЧУВСТВИТЕЛЬНОСТИ?

 

Несмотря на все свои преимущества — теоретическую прозрачность, простоту расчетов, экономико-математическую естественность результатов и наглядность их толкования (именно эти критерии и лежат в основе его широкой практической применимости), — метод анализа чувствительности имеет существенные недостатки.  Первый и основной из них — его однофакторностъ, т. е. ориентация на изменения только одного фактора проекта. При этом не принимается во внимание возможная связь между отдельными факторами, или их корреляция. Кроме того, по своей основе этот метод является экспертным, т. е. разные группы экспертов могут получить различные результаты.

 

В ЧЕМ ЗАКЛЮЧАЕТСЯ МЕТОД «АНАЛИЗ СЦЕНАРИЕВ»?

 

Следующий метод, применяемый при количественной оценке риска, — анализ сценариев — позволяет отчасти исправить недостаток предыдущего метода, так как включает одновременное (параллельное) изменение факторов проекта, проверяемых на риск. По существу, этот метод анализа рисков инвестиционного проекта представляет собой развитие методики анализа чувствительности, заключающееся в одновременном непротиворечивом (реалистическом) изменении всей группы переменных проекта, проверяемых на риск.

 

В результате определяется воздействие одновременного изменения всех основных переменных проекта, характеризующих его денежные потоки, на критерии проектной эффективности. Важным преимуществом этого метода является тот факт, что отклонения параметров рассчитываются с учетом их взаимозависимостей (корреляции).

 

В качестве возможных вариантов целесообразно построить как минимум три сценария: пессимистический, оптимистический и наиболее вероятный (реалистический, или средний).

 

Построение пессимистического сценария связано с ухудшением значений переменных параметров до определенного разумного уровня по сравнению с базовыми (реалистическими). На основании полученных значений факторов (например цен на продукцию, объемов производства, капитальных вложений, текущих издержек, налоговых платежей и т. д.) рассчитываются значения критериев эффективности проекта (NPV, IRR и др.). Полученные значения сравниваются с их базисными значениями, и формулируются необходимые рекомендации. В основе рекомендаций лежит обязательное условие: даже в оптимистическом варианте нет возможности оставить проект для дальнейшего рассмотрения, если рассчитанное значение находится за пределами эффективности проекта (например,  NPV  проекта отрицательно), и, наоборот, при пессимистическом сценарии получение, например, положительного значения NPV позволяет говорить о приемлемости данного проекта.

 

Итак, анализ чувствительности и сценарный анализ являются последовательными шагами в количественном анализе рисков, при этом последний позволяет избавиться от некоторых недостатков метода анализа чувствительности. Однако следует отметить, что метод сценариев наиболее эффективно применим в случае, когда количество возможных значений NPV конечно. Вместе с тем, как правило, при проведении анализа рисков инвестиционного проекта эксперт сталкивается с неограниченным количеством различных вариантов развития событий.

 

Проведение анализа рисков проекта требует использования компьютерной техники и программных продуктов. Реализация и построение моделей сценарного подхода возможны, например, на основе электронных таблиц типа Excel, что помогает значительно упростить работу.

 

МЕТОД СТАВКИ ПРОЦЕНТА С ПОПРАВКОЙ НА РИСК.

 

Чем выше инвестор оценивает риск проекта, тем более высокие требования он обычно предъявляет к его доходности. Это может быть отражено в расчетах путем соответствующего увеличения нормы дисконта — включения в нее премии за риск.

 

Существуют две группы методов — агрегированные и пофакторные (кумулятивные), учитывающие, соответственно, риск сразу целиком и каждый вид риска в отдельности.

АГРЕГИРОВАННЫЕ МЕТОДЫ.

 

МЕТОД БЕТА-КОЭФФИЦИЕНТА (концепция β-коэффициента).

 

Метод бета-коэффициента для расчета нормы дисконта использует модель оценки капитальных активов (Capital Assets Prices Model — САРМ):

 

R=R_f + β∙(R_m – R_f),

 

где R — требуемая инвестором ставка дохода (на собственный капитал),

 

R_f — безрисковая ставка дохода;

 

β — коэффициент бета;

 

R_m — общая доходность рынка в целом (среднерыночного портфеля ценных бумаг).

Данная модель основана на анализе массивов информации фондового рынка, конкретно — изменения доходности свободно обращающихся акций.

 

В качестве безрисковой ставки дохода в мировой практике используется обычно ставка дохода по долгосрочным государственным долговым обязательствам; считается, что государство является самым надежным гарантом по своим обязательствам (вероятность его банкротства практически исключается).  В общем случае, для определения ставки дисконта в качестве безрисковой может быть принята ставка по вложениям, характеризующимся наименьшим уровнем риска. Безрисковая ставка используется как точка отсчета, к которой привязывается оценка различных видов риска, характеризующих вложения в данное предприятие, на основе чего и выстраивается требуемая ставка дохода.

 

Среднерыночная доходность должна рассматриваться как известная абстракция, поскольку полная информация о доходности всех обращающихся на рынке акций обычно отсутствует. На практике этот показатель рассчитывают по ограниченному числу представительных ценных бумаг, например по акциям «голубых фишек».

 

ЧТО ПРЕДСТАВЛЯЕТ СОБОЙ КОЭФФИЦИЕНТ БЕТА?

 

Коэффициент бета представляет собой меру риска. На фондовом рынке выделяются два вида риска: специфический для конкретной компании, еще называемый НЕСИСТЕМАТИЧЕСКИМ (определяется микроэкономическими факторами), и общерыночный, характерный для всех компаний, акции которых находятся в обращении, называемый также СИСТЕМАТИЧЕСКИМ (вызван макроэкономическими и политическими причинами).

 

В МОДЕЛИ ОЦЕНКИ КАПИТАЛЬНЫХ АКТИВОВ ПРИ ПОМОЩИ КОЭФФИЦИЕНТА БЕТА ОПРЕДЕЛЯЕТСЯ ВЕЛИЧИНА СИСТЕМАТИЧЕСКОГО РИСКА.

КАК ОПРЕДЕЛЯЕТСЯ ВЕЛИЧИНА КОЭФФИЦИЕНТА БЕТА?

 

Для определения величины коэффициента бета используют два метода.

 

1. Первый метод основывается на анализе коэффициентов бета действующих предприятий-аналогов. Такой расчет производится в два этапа.

 

ЭТАП 1.  На первом этапе выбирается анализируемый период, и собираются необходимые данные о доходности акций предприятия и о среднерыночной доходности на отдельные даты в этом периоде. Для m-го наблюдения обозначим указанные показатели через d_m и R_m .

 

При увеличении объема такой информации расчеты становятся более точными, однако если при этом анализируемый период «расширяется в прошлое», то получаемые значения коэффициента бета (β)   с меньшей долей уверенности можно будет распространить на перспективу.

 

ЭТАП 2. На втором этапе по отдельным конкретным величинам d_m и R_m вначале рассчитываются средние за период значения доходности d_cp. и R_cp.,  а затем вычисляется коэффициент бета (β) по следующей формуле:

 

β =(Σ_m (d_m – d_ср.)∙(R_m – R_ср.))/(Σ_m (R_m – R_ср.)²).

 

(12)

Подобные коэффициенты для различных предприятий и групп предприятий рассчитываются многими специалистами и агентствами и часто публикуются в прессе.

 

2. Второй подход к определению коэффициента бета опирается на анализ показателей и характеристик деятельности компании, которые предположительно влияют на степень инвестиционного риска. Подобный коэффициент называется «фундаментальным». Определение фундаментального бета основано на исследовании, которое выявляет тесную корреляцию между коэффициентом бета и показателями риска предприятия. Показатели риска включают следующее:

 

- финансовые риски, которые рассчитываются на основе финансовой отчетности компании и включают анализ тенденций и сравнительный анализ финансовых коэффициентов;

 

- отраслевые риски;

 

- влияние изменений общеэкономической ситуации на деятельность компании.

 

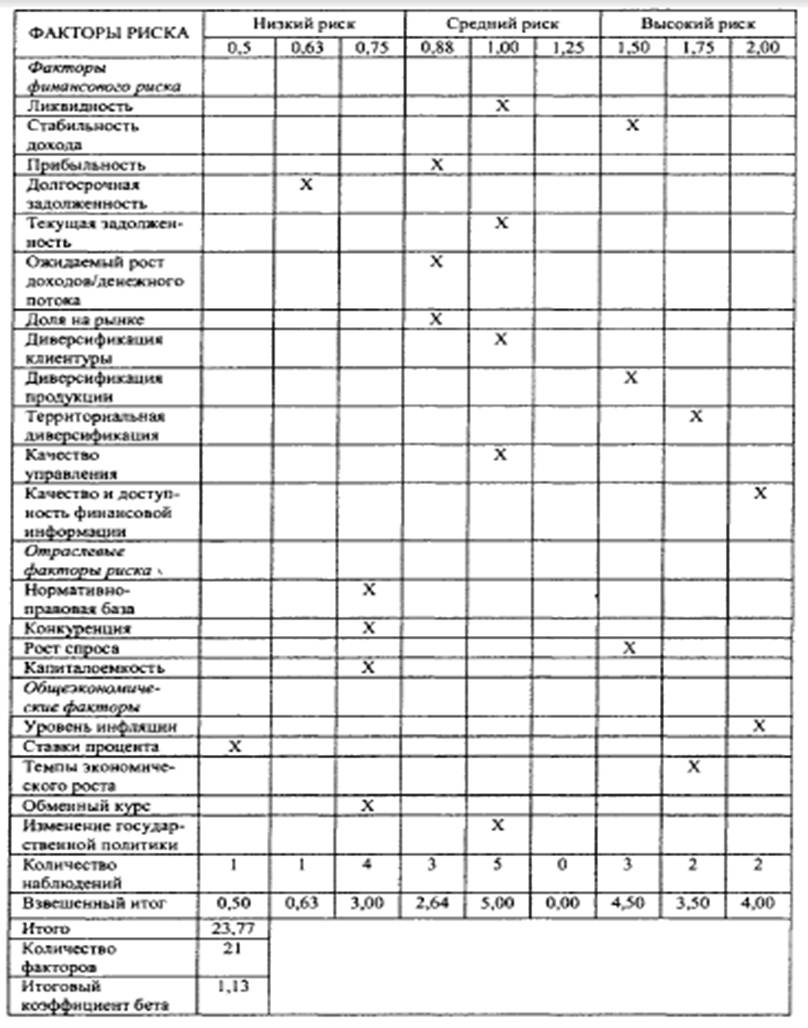
В таблице 4 содержится анализ 21 финансового, отраслевого и общеэкономического фактора риска, а также в качестве примера отражено мнение эксперта относительно влияния каждого фактора на риск инвестирования в некий проект.

 

Таблица 4. Анализ факторов риска с мнением эксперта.

 

КАК ИНТЕРПРЕТИРУЕТСЯ ЗНАЧЕНИЕ ФУНДАМЕНТАЛЬНОГО БЕТА ДЛЯ КОМПАНИИ?

 

Обычно коэффициент бета лежит в пределах от 0 до 2. Коэффициент бета для рынка в целом равен 1. Если у какой-либо компании коэффициент бета равен 1, то колебания ее общей доходности полностью коррелируют с колебаниями доходности рынка в целом и ее систематический риск равен среднерыночному риску. Общая доходность компании, у которой коэффициент бета равен 1,5, будет изменяться на 50% быстрее доходности рынка. Например, если среднерыночная доходность акций снизится на 10%, общая доходность данной компании упадет на 15%.

 

КАКОВЫ ОСОБЕННОСТИ МЕТОДА БЕТА-КОЭФФИЦИЕНТА?

 

Следует отметить ряд важных особенностей бета-метода, которые необходимо учитывать при попытках его применения.

 

1. В данном методе термином «риск» охватываются любые положительные или отрицательные отклонения доходности проекта от среднего значения. Тем самым если оценивать эффективность проекта, ориентируясь только на базовый сценарий его реализации (а именно для этой ситуации обычно применяется β-метод), то в этом сценарии должны быть предусмотрены средние, а не умеренно пессимистические значения всех показателей. Поэтому при применении бета-метода все технико-экономические параметры проекта должны быть скорректированы в сторону улучшения.

 

2. Как ни была бы похожа продукция предприятия-аналога и проектируемого, цена акций первого определяется не только этим, но и другими факторами (например, структурой капитала, дивидендной политикой и степенью диверсификации производства). Играет роль и то обстоятельство, что взаимоотношения с государством у них могут быть различными. Поэтому некритическое распространение значения β на другие предприятия неправильно.

 

3. В «чистом виде» β-метод учитывает только один тип рисков — СИСТЕМАТИЧЕСКИЙ. Этот недостаток поправим путем внесения в него дополнительных поправок на другие виды рисков. Для выравнивания результатов «чистого» β-метода до β-«фундаментального» перечень несистематических рисков следует, как минимум, соотнести со списком факторов финансового риска (таблица 4).

 

МЕТОД СРЕДНЕВЗВЕШЕННОЙ СТОИМОСТИ КАПИТАЛА.

 

Необходимо отметить, что метод β-коэффициента используется при установлении нормы дисконта для денежного потока только собственного капитала. Если необходимо установить норму дисконта для денежного потока всего инвестированного капитала, используют метод средневзвешенной стоимости капитала (Weighted Average Cost of Capital — WACC). В наиболее простом случае, когда в структуре инвестированного капитала вычленяются только собственные и заемные средства (без их дальнейшего подразделения), расчетная формула для нормы дисконта имеет вид:

 

R_WACC=R_c∙g_c + R_з.∙g_з. ,

 

(13)

 

где R_c — стоимость собственного капитала (требуемая отдача на акции),

 

R_з. — стоимость заемного капитала (ставка процента по займу),

 

g_c , g_з. — доли собственного и заемного капитала, соответственно, в общем капитале проекта.

В литературе часто встречается модификация указанной формулы.

 

По существующему западному законодательству, проценты по займу исключаются при налогообложении прибыли, так что, используя кредиты, фирма получает налоговую льготу, что эквивалентно для нее выплате процентов в меньшем размере. В результате формула (13) для расчета нормы дисконта принимает вид:

 

R_WACC=R_c∙g_c + R_з.∙g_з. ∙(1- t),

 

(14)

 

где t — ставка налога на прибыль предприятия.

В ЧЕМ ЗАКЛЮЧАЮТСЯ ТРУДНОСТИ ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ МЕТОДА WACC?

 

Оценим данный метод с точки зрения возможностей практического использования. Метод WACC применим к небольшим проектам, реализуемым на действующих предприятиях. Все входящие в формулу параметры должны задаваться в исходной информации о фирме, причем обычно берутся последние фактические данные о фирме, а получаемая норма дисконта распространяется на весь период осуществления проекта.

 

Однако, работая с данным методом, необходимо прогнозировать входящие в формулу параметры на перспективу и устанавливать норму дисконта переменной во времени.

 

Неоднозначно решается вопрос и о том, как устанавливать доли собственного и заемного капитала. К сравнительно крупным проектам, реализуемым на действующих предприятиях, применяются два варианта.

 

1. Первый вариант предусматривает, что веса g_c и g_з. устанавливаются по всей фирме. При этом очевидно, что в норме дисконта отражается риск, связанный с деятельностью фирмы в целом, а не риск, относящийся к данному проекту. Это может рассматриваться как недостаток метода. Но такой подход позволяет учесть то обстоятельство, что, реализуя разные проекты, фирма старается поддерживать определенную структуру своего капитала, и тем самым как бы устраняет их риски. В этом варианте норма дисконта на протяжении всего расчетного периода оказывается стабильной.

 

2. При втором варианте в формулы включается структура капитала, относящаяся не к фирме, а к рассматриваемому проекту. Это мотивируется тем, что данный вариант в отличие от первого приводит к переменной по шагам норме дисконта, что несколько усложняет оценку эффективности. Но как именно будет меняться норма дисконта во времени? Если на начальном этапе предусматривается получение большого займа, то в процессе реализации проекта и погашения долга доля собственного капитала, а значит, и норма дисконта будут возрастать. Между тем совершенно очевидно, что для самой фирмы, ее акционеров и кредитора риск проекта должен уменьшаться по мере того, как проект осуществляется, а заем погашается. Таким образом, динамику нормы дисконта второй вариант метода отражает неадекватно.

 

КУМУЛЯТИВНЫЙ МЕТОД ОЦЕНКИ РИСКОВ.

 

Данный метод исходит из определенной классификации факторов риска и оценок каждого из них. За базу расчетов берется безрисковая ставка. Принимается, что каждый фактор увеличивает данную ставку на определенную величину, и общая премия получается путем сложения «вкладов» отдельных факторов. Классификация факторов и размеры их «вкладов» могут быть различными. Вот одна из возможных таблиц для такого расчета (таблица 5), в основе которой заложены материалы Мирового банка и аудиторской фирмы «Большой пятерки» — Deloitte & Touche.

 

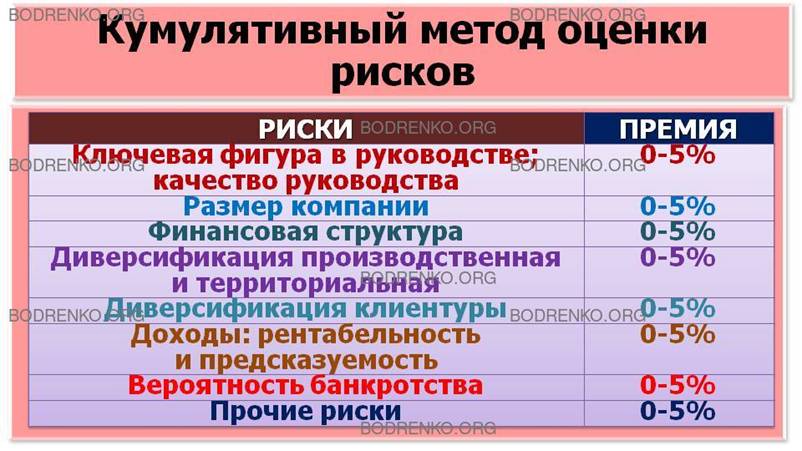
Таблица 5. Пример таблицы расчета рисков кумулятивным методом.

 

РИСКИ	ПРЕМИЯ
Ключевая фигура в руководстве; качество руководства	0-5%
Размер компании	0-5%
Финансовая структура	0-5%
Диверсификация производственная и территориальная	0-5%
Диверсификация клиентуры	0-5%
Доходы: рентабельность и предсказуемость	0-5%
Вероятность банкротства	0-5%
Прочие риски	0-5%

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

[1] Бузова И. А., Маховикова Г. А., Терехова В. В. Коммерческая оценка инвестиций /под ред. Есипова В.Е. — СПб.: Питер,  2004. — 432 с.: ил. — (Серия «Учебник для вузов»).

 

[2] Грачева Я. Б. Анализ проектных рисков: Учеб.пособие для вузов. — М.: ЗАО «Финстатинформ», 1999.

[3] Мельников А.В., Попова Н.В., Скорнякова B.C. Математические методы финансового анализа. — М.: «Анкил», 2006. — с. 440.

 

[4] Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. М.: Инфра-М., 1997. 

 

[5] Экономическая оценка инвестиций /под ред.  проф. М.И. Римера. 3-е изд., перераб. и доп. (+CD с учебными материалами). — СПб.: Питер, 2009. —416 с: ил. — (Серия «Учебник для вузов»).