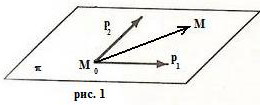
Пусть плоскость π с направленными векторами p1 и
p2 проходит через точку М0. Очевидно, точка М лежит в плоскости π тогда и только тогда, когда (рис. 1) векторы 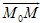 , p1,
p2 компланарны, т.е. линейно зависимы.
, p1,
p2 компланарны, т.е. линейно зависимы.
С учетом условия неколлиниарности векторов p1 и
p2 это равносильно тому, что вектор 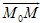 линейно выражается через p1 и p2:
линейно выражается через p1 и p2:
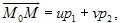
u, v ∈ R. (5.3.1)
Теорема 5.6. В пространстве в аффинной системе координат Oxyz уравнение плоскости π, проходящей через точки
М0(x0, y0, z0), с направляющими вектороми p1 = {m1, n1, k1} и
p2 = {m2, n2, k2} имеет вид
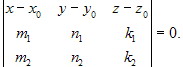
(5.3.2)
Доказательство теоремы повторяет доказательство теоремы 5.2.
Уравнеие (5.3.2) называется каноническим уравнением плоскости.
Cледствие 2.
Уравнение плоскости, проходящей через три точки
М0(x0, y0, z0), М1(x1, y1, z1) и
М2(x2, y2, z2), не лежащие на одной прямой, имеет вид
Параметрическое уравнение.Так же, как для прямой, условие (5.3.1) может быть переписано в виде
r = r0 + up1 + v2, u, v ∈ R, (5.3.3)
или, в координатной форме, в системе координат Oxyz
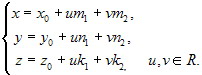
(5.3.4)
Уравнения (5.3.3), (5.3.4) называются параметрическими уравнениями плоскости в векторной и координатной формах.
Теорема 5.7. Поверхность в пространстве является плоскостью тогда и только тогда, когда она является алгебраической
поверхностью первого порядка.
Доказательство теоремы повторяет доказательство теоремы 5.3 с той лишь разницей, что уравнение
плоскости имеет вид
Ax + By + Cz + D = 0, где A2 + B2 + C2≠ 0,
(5.3.5).
а уравнение (5.3.5) может быть записано в виде
(случаи B ≠ 0 и C ≠ 0 рассматриваются аналогично). Теорема доказана.
Уравнение (5.3.5) называется общим уравнением плоскости в пространстве. Вектор n = {A, B, С} называется вектором нормали к плоскости относительно уравнения (5.3.5).
Общее уравнение плоскости называется полным, если все коэффициенты А, В, С, D отличны от нуля.
Теорема 5.8. В аффинной системе координат Oxyz в пространстве вектор а = {m, n, k}, параллелен плоскости, заданной
общим уравнением (5.3.5), тогда и только тогда, когда
Am + Bn + Сk = 0,
(5.3.6)
Доказательство теоремы повторяет доказательство теоремы 5.4.
Теорема доказана.
Замечание 3. Левые части условия (5.3.6) можно рассматривать как скалярные произведения
вектора нормали n и вектора а в ортонормированном базисе. Таким образом, в прямоугольной декартовой системе координат вектор нормали n = {A, B, С} к плоскости (5.3.5) перпендикулярен этой плоскости.
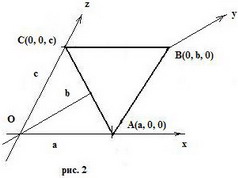
Уравнение в отрезках. Полное уравнение (5.3.5) плоскости в пространстве может быть записано в следующем виде:
Полагая а = - D/А, b = - D/B, c = - D/C, получим эквивалентное уравнение
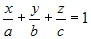
,
Векторное уравнение. 1. Параметрическое уравнение (5.3.3) представляет собой векторное уравнение плоскости
в пространстве через направляющие вектора. Оно пораждает другие формы векторных уравнений плоскости. Это уравнение означает компланарность векторов r - r0, p1 и
p2, что согласно критерию компланарности
(теорема 4.7) равносильно равенству
( r - r0, p1, p2) = 0
(5.3.7)
или, в силу линейности смешанного произведения, (r, p1, p2) = D
(5.3.8)
где D − константа, равная (r0, p1, p2).
2.
Из аксиом геометрии следует, что в пространстве через заданную точку проходит единственная плокость, перпендикулярная заданному вектору.
Теорема 5.9. Уравнение плоскости в пространстве, проходящей через точку М0(r0) перпендикулярно вектору n,
имеет вид
( r - r0, n) = 0,
(5.3.9)
или, что то же самое,( r, n) = D,
(5.3.10)
где D − константа, равная (r0, n).
Доказательство.Утверждение теоремы вытекает из того, что точка M(r) лежит на плоскости тогда итолько тогда, когда векторы
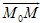 и n ортогональны. Теорема доказана.
и n ортогональны. Теорема доказана.
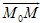 , p1,
p2 компланарны, т.е. линейно зависимы.
, p1,
p2 компланарны, т.е. линейно зависимы. 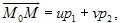 u, v ∈ R. (5.3.1)
u, v ∈ R. (5.3.1)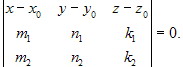 (5.3.2)
(5.3.2)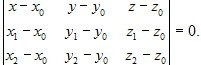
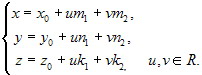 (5.3.4)
(5.3.4)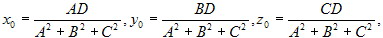
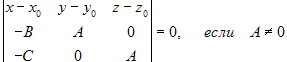
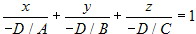
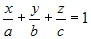 ,
, 