Если а ≠ 0, то для любого вектора b
(a, b) = |a| (prab) = (a, prab).
4.1.2
Доказательство.
Утверждение теоремы очевидно для b = 0 и  Пусть b ≠ 0 и
Пусть b ≠ 0 и 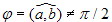 . Тогда (рис. 1)
. Тогда (рис. 1)
Отсюда следует, что
(prab) = |b| cos φ и, тем самым, (a, b) = |a| (prab). Вторая часть соотношения (4.1.1) вытекает из первой, так как praprab = prab.
Теорема доказана.
Теорема 4.2. Для любых векторов a, b, с и числа α ∈ R
- (a, b) = (b, a);
- (a + b, c) = (a, c) + (b, c);
- (αa, b) = α(a, b);
- (a, a) ≥ 0, причем (a, a) = 0 тогда и только тогда, когда а = 0.
Доказательство.Свойства 1 и 4 очевидны. Докажем свойство 2. Имеем (a + b, c) = (с, a + b) = |c| (prc(a + b)) =
{cогласно теореме 3.5} = |c| (prca) + |c| (prcb) = (a, c) + (b, c). Аналогично проверяется свойство 3.Теорема доказана.
Следствие 1. Из свойств 1-3 следует, скалярное произведение линейно и по второму множителю: (a, b + c) =
(a, b) + (a, c), (a, αb) = α(a, b).
Скалярное произведение в координатах.
Свойство линейности скалярного произведения позволяет перемножатьлинейные комбинации векторов (т.е. находить их скалярное произведение):
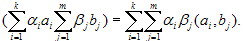
4.1.3
Это, в частности, означает, что скалярное произведение векторов может быть вычесленно
по их координатам, если известна "таблица умножения" базисных векторов. Возможность подобного вычисления скалярного произведения векторов позволяет определить по координатам длину вектора и
угол между векторами, так как 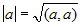 ,
, 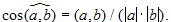
Задача вычисления скалярного произведения векторов по их координатам существенно упрощается,
если рассматривается ортонормированный базис. Векторы a и b называются ортогональными, если (a, b) = 0. Из определения следует, что векторы a и b ортогональны тогда и только тогда,
когда либо один из них нулевой, либо они перпендикулярны. В терминах ортогональности векторов ортонормированность базиса е1, … ,en, где n=1, 2, 3, означает, что
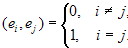
4.1.4
Теорема 4.3. Скалярное произведение векторов а = α1e1 +
α2e2 + α3e3 и b = β1e1 + β2e2 + β3e3
равно сумме попарных произведений координат 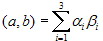
4.1.5
Следствие 2. Если векторы а = {α1,α2, α3},
b = {β1, β2, β3} заданы координатами в ортонормированном базисе, то 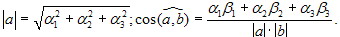
4.1.6
Следствие 3. В прямоугольной декартовой системе координат
расстояние ρ(A, B) между точками А(x1, y1, z1) и B(x2, y2, z2) равно
Это равенство следует из того, что 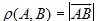 и
и  .
. 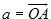 ,
, 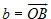 . Угол между векторами a и b называется наименьший угол между лучами [OA) и [OB).
Обозначение:
. Угол между векторами a и b называется наименьший угол между лучами [OA) и [OB).
Обозначение: 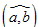 . Корректность определения очевидна. Из определения следует, что 0 ≤
. Корректность определения очевидна. Из определения следует, что 0 ≤ 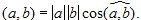 4.1.1
4.1.1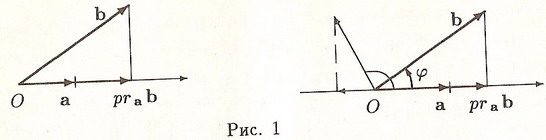
 Пусть b ≠ 0 и
Пусть b ≠ 0 и 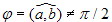 . Тогда (рис. 1)
. Тогда (рис. 1) 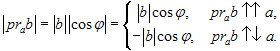
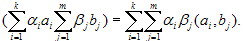 4.1.3
4.1.3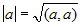 ,
, 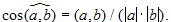
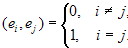 4.1.4
4.1.4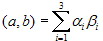 4.1.5
4.1.5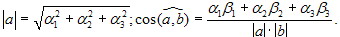 4.1.6
4.1.6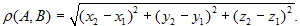
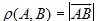 и
и  .
.