Теория риска и моделирование рисковых ситуаций. Матричные игры. Конечные антагонистические игры. Исходная модель матричной игры. Платежная матрица. Верхняя и нижняя цена игры. Понятие нулевой суммы. Стратегии игроков. Ситуации равновесия. Седловые точки. Нахождение седловых точек. Смешанные стратегии. Теорема Неймана
Решение задач и выполнение научно-исследовательских разработок: Отправьте запрос сейчас: irina@bodrenko.org
математика, IT, информатика, программирование, статистика, биостатистика, экономика, психология
Пришлите по e-mail: irina@bodrenko.org описание вашего задания, срок выполнения, стоимость
Теория риска и моделирование рисковых ситуаций.
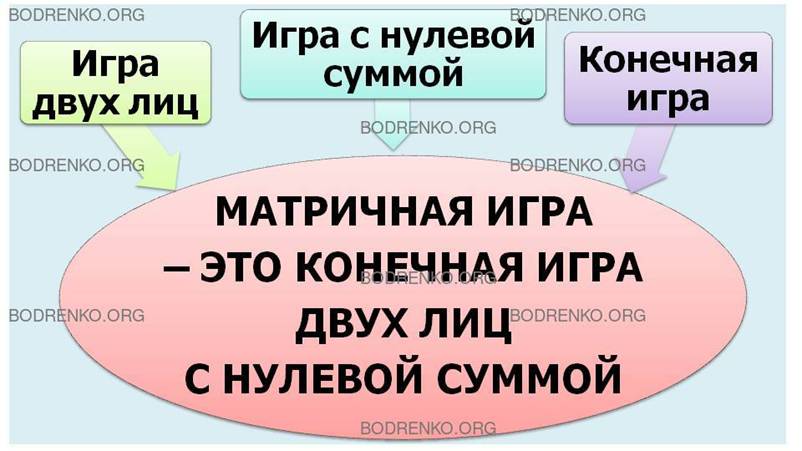
Лекция 2. Матричные игры.

1. Конечные антагонистические игры. Матричные игры.
2. Исходная модель матричной игры. Понятие нулевой суммы. Платежная матрица.
3. Стратегии игроков. Верхняя и нижняя цена игры. Ситуации равновесия (седловые точки). Нахождение седловых точек.

1. КОНЕЧНЫЕ АНТАГОНИСТИЧЕСКИЕ ИГРЫ. МАТРИЧНЫЕ ИГРЫ.
1.1.ЗАДАЧИ ТЕОРИИ ИГР В ЭКОНОМИКЕ.
Во многих задачах финансово-экономической сферы, в частности, в задачах маркетинга, менеджмента, финансово-банковских операций, инвестиций в различные проекты и т. д. возникает необходимость принятия решений. Проблема принятия решений осложняется тем, что ее приходится решать в условиях неопределенности.
Неопределенность может носить различный характер.
Неопределенными могут быть осознанные действия противоборствующей стороны, направленные на уменьшение эффективности решений, принимаемых противной стороной. Например, фирмы, конкурирующие на одном рынке, осуществляют действия, которые приводят к реализации своих интересов и препятствуют в этом конкурентам.
Неопределенность может относиться и к ситуациям риска, в которых сторона, принимающая решение, в состоянии установить все возможные результаты своих решений, вместе с вероятностями их появления. Эти вероятности представляют собой вероятности всевозможных условий, в которых решается данная задача. Условия, о которых идет речь, влияют на принятие решений неосознанно и формируются из многих факторов (общего состояния экономической и финансовой систем, курсов валют, уровня инфляции и т. д.).

Если же известны все возможные последствия принимаемых решений, но неизвестны их вероятности, то есть неизвестны вероятности возможных состояний внешней среды, окружающей решаемую задачу, то говорят, что решение принимается в условиях полной неопределенности.
Кроме того, неопределенностью может обладать и цель решаемой задачи, когда показатель эффективности принимаемого решения характеризуется единственным числом и не всегда отражает достаточно полную картину.
В условиях полной определенности теоретические и практические выводы носят однозначный характер и представляют собой четкое описание ситуации в рамках рассматриваемой модели (задачи).
В условиях же недостаточной информированности или полной неопределенности результаты анализа уже не обладают такой четкостью и однозначностью. Однако полученные при этом рекомендации оказываются полезными при выборе решений, так как они дают возможность обосновать варианты принимаемых решений с разных точек зрения (порой противоположных).
Попытка количественного анализа финансово-экономических ситуаций и принятия на их основе определенных решений и привела к созданию специальных экономико-математических методов обоснования выбора и принятия решений в условиях рыночной экономики. Такие методы позволяют находить количественные характеристики экономических процессов.
Это позволяет в одних, более простых и более определенных ситуациях, находить оптимальное решение, а в других, более сложных и неопределенных ситуациях, такие методы приводят к получению дополнительной информации, позволяющей провести детальный анализ каждого варианта решения, выявить его положительные и отрицательные стороны и остановиться на том варианте решения, которое будет более или менее полно проанализированным и предпочтительным для стороны, принимающей решение.
При выборе решения в условиях неопределенности всегда присутствует фактор действия наудачу без обоснованной уверенности в правильности принимаемого решения. То есть выбор решения в условиях неопределенности всегда сопряжен с риском.
Математические методы обоснования принимаемых в экономике решений дают возможность анализа различных вариантов решения с целью уменьшения уровня риска, которое иногда достигается за счет получения дополнительной информации. В этом случае возникает проблема расчета стоимости этой информации, приобретение которой позволит максимизировать экономический эффект принимаемого решения.
Математизация содержательных финансово-экономических задач о принятии решений в условиях неопределенности и риска приводит к соответствующим экономико-математическим моделям и методам, теоретический аспект которых составляет теорию игр.
Таким образом, задачами теории игр в экономике являются задачи о выборе решений в условиях экономической неопределенности и риска.
Содержание управления экономикой сводится к постоянному выбору оптимальных решений. От того, насколько эффективны принимаемые решения, зависит состояние производственно-технологической и социальной сфер экономики.
Сложный характер рыночной экономики предъявляет серьезные требования к обоснованию принятия решений. Одним из способов удовлетворения этих требований является постановка задач принятия решений на математическую основу.
Математическое описание постановок различных задач по принятию решений и математическое обоснование подходов к их анализу и решению помогают лицу, принимающему решение, провести критический анализ ситуации, и в результате более обоснованно и последовательно осуществлять определенную стратегию поведения при решении сложных экономических проблем.
Теория игр представляет собой теоретические основы математических моделей принятия оптимальных решений в конфликтных ситуациях рыночных отношений, носящих характер конкурентной борьбы, в которых одна противоборствующая сторона выигрывает за счет другой стороны.
Наряду с такой ситуацией в теории принятия решений рассматривают также ситуации риска и неопределенности, которые имеют различные модели и требуют разных критериев выбора оптимальных решений.
Теория игр получила широкое распространение и используется в различных областях экономики и производства, бизнеса и финансов, сельского хозяйства, военного дела, биологии и социологии, психологии и политологии. К настоящему времени теория игр развилась в самостоятельную область математики и может рассматриваться независимо от ее приложений к реальным игровым ситуациям.
1.2.КОНФЛИКТЫ И ТЕОРИЯ ИГР.
В практической деятельности часто приходится рассматривать явления и ситуации, в которых участвуют две (или более) стороны, имеющие различные интересы и обладающие соответствующими возможностями применять для достижения своих целей разнообразные действия. Подобные явления и ситуации называются конфликтными или просто конфликтами.
Типичная конфликтная ситуация характеризуется тремя основными составляющими:
1) заинтересованными сторонами (это потребители, фирмы, отдельные страны, финансовые и экономические союзы и т. д.);
2) интересами сторон (удовлетворение различных финансовых, экономических и политических потребностей, вытеснение конкурентов с рынка сбыта, повышение доходов и т. д.);
3) их возможными действиями (выбор объема потребления, способы формирования инвестиционного портфеля, выбор объема производства, выбор дивидендной политики и «демпинговая» политика и т. д.).

Любая конфликтная ситуация, взятая из реальной жизни, как правило, довольно сложна.
Ее изучение затруднено наличием многих разных обстоятельств, часть из которых не оказывает сколь-нибудь существенного влияния ни на развитие конфликта, ни на его исход.
Поэтому для того, чтобы анализ конфликтной ситуации оказался возможным, необходимо удалить эти второстепенные факторы, что при удачном стечении обстоятельств позволяет построить упрощенную формализованную математическую модель конфликта, которую принято называть игрой и которая отличается от реальной конфликтной ситуации еще и тем, что ведется по вполне определенным правилам.
Необходимость изучения и анализа конфликтов, представляемых в виде упрощенных моделей (игр) вызвала в жизни специальный математический аппарат — теорию игр. Обычно теорию игр определяют как раздел математики для изучения конфликтных ситуаций. Это значит, что можно выработать оптимальные правила поведения каждой стороны, участвующей в разрешении конфликтной ситуации.
Кроме того, в экономике, например, оказался недостаточным аппарат математического анализа, занимающийся определением экстремума функций. Появилась необходимость изучения так называемых оптимальных минимаксных и максиминных решений.
Следовательно, теорию игр можно рассматривать как раздел методов оптимизации, позволяющий решать задачи теории принятия решений, в частности управленческих решений в экономике.
Математико-игровые модели находят свое применение не только в конфликтных ситуациях социально-экономической области, но и во взаимодействии человека с природой, в политике,
биологии, военной области и т. д.
Игра — это упрощенная формализованная модель реальной конфликтной ситуации. Формализация означает выработку определенных правил действия сторон в процессе игры: варианты действия сторон, исход игры при данном варианте, степень информированности каждой стороны о поведении всех других сторон.
Заинтересованные играющие стороны (в частности, лица) называются игроками. Причем одну играющую сторону может представлять как один игрок, так и целый коллектив.
Стратегией игрока называется любое возможное для игрока действие в рамках заданных правил игры. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемых ситуацией.
Заинтересованность игроков в ситуации проявляется в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем в ней. Хотя не каждый выигрыш можно оценить количественно, но в теории игр качественные выигрыши не рассматриваются.
Изучение теории игр можно проводить с различных точек зрения. Мы будем стремиться решать следующие задачи:
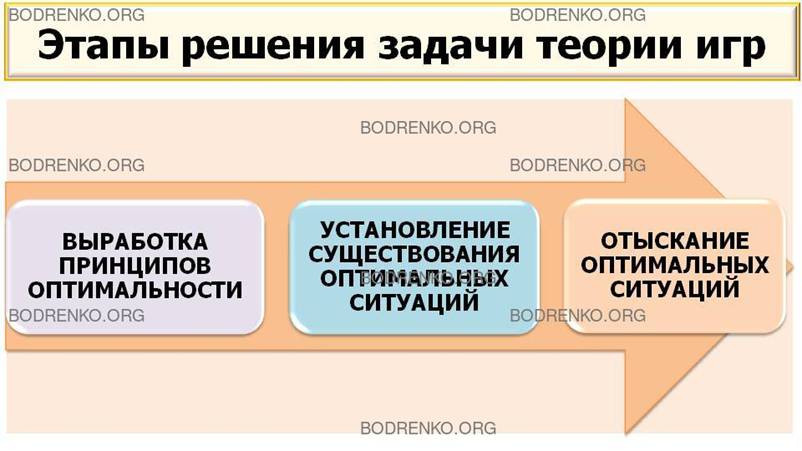
1. Выработка принципов оптимальности, то есть того, какое поведение игроков следует считать разумным или целесообразным.
2. Выяснение реализуемости принципов оптимальности, то есть установление существования оптимальных ситуаций (и стратегий).
3. Отыскание оптимальных ситуаций (реализация игры).
Отметим также, что оценка игроком ситуации путем указания его количественного выигрыша, вообще говоря, возможна не всегда, а иногда просто не имеет смысла.
В этом случае численное значение выигрыша в каждой ситуации заменяют на сравнительную предпочтительность ситуаций для отдельных игроков.
Тогда речь ведут о теории игр с предпочтениями, которая включает в себя теорию игр с выигрышами как частный случай.
Таким образом, основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявления для каждого из них «оптимальной стратегии».

Понятие оптимальной стратегии — одно из важнейших понятий теории игр, может пониматься в различных смыслах в зависимости от показателя оптимальности (эффективности). Стратегия, оптимальная по одному показателю, может не быть оптимальной по другому показателю. Поэтому чаще всего оптимальная стратегия, определенная в результате применения теории игр к реальным конфликтным ситуациям, является оптимальной теоретически и в большинстве случаев реально удовлетворительной.
1.3. КЛАССИФИКАЦИЯ ВИДОВ ИГР.
В теории игр не существует установившейся классификации видов игр. Однако по определенным критериям некоторые виды игр можно выделить. Игры можно классифицировать по следующим критериям.
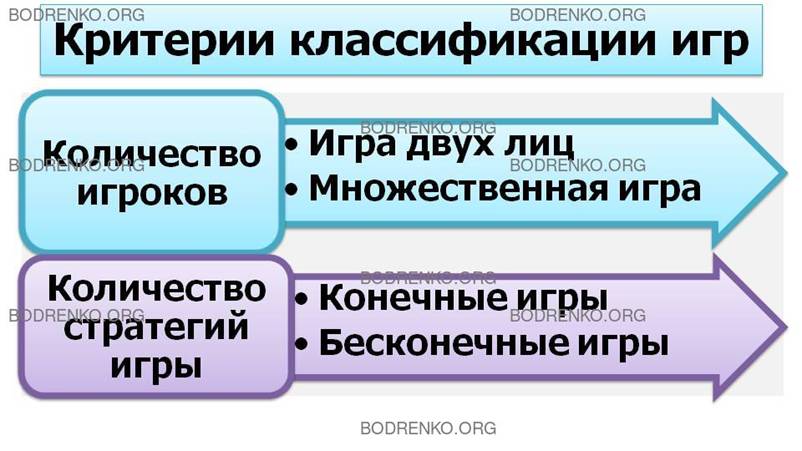
1. Количество игроков. Если в игре участвуют две стороны, то ее называют игрой двух лиц. Если число сторон больше двух, ее называют игрой N лиц (или множественной). Наиболее глубоко проработаны игры двух лиц.
2. Количество стратегий игры. По этому критерию игры делятся на конечные и бесконечные. В конечной игре каждый из игроков имеет конечное число возможных стратегий.
Игра является бесконечной, если хотя бы один из игроков имеет бесконечное число возможных стратегий.
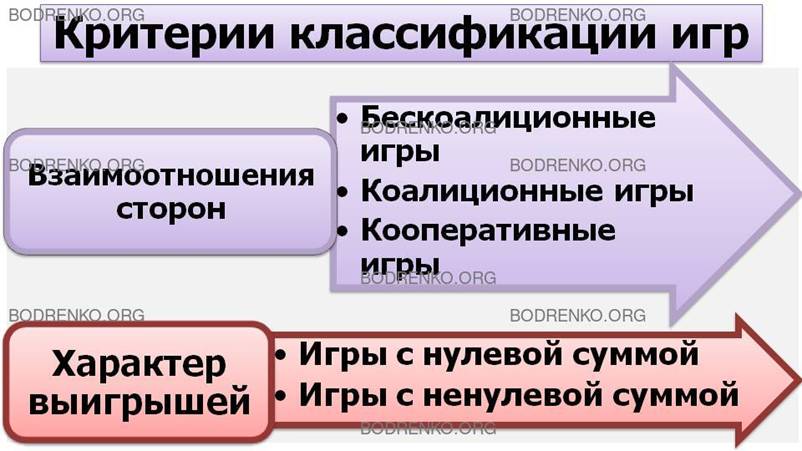
3. Взаимоотношения сторон. Согласно этому критерию игры подразделяются на бескоалиционные, коалиционные и кооперативные.
Бескоалиционной называется игра, в которой игроки не имеют права вступать в соглашения, образовывать коалиции.
В коалиционной игре игроки могут вступать в соглашения, создавать коалиции.
Если коалиции определены заранее, то такая игра называется кооперативной.
4. Характер выигрышей. По этому критерию игры подразделяются на игры с нулевой суммой и игры с ненулевой суммой.
Игра с нулевой суммой означает, что сумма выигрышей всех игроков в каждой партии равна нулю. Игры двух игроков с нулевой суммой относятся к классу антагонистических игр.
При этом выигрыш одного игрока равен, естественно, проигрышу другого игрока. Примерами игр с нулевой суммой служат многие экономические задачи. В них общий капитал всех игроков перераспределяется между игроками, но не меняется.
Игра, в которой нужно вносить взнос за право участия в ней, является игрой с ненулевой суммой. К играм с ненулевой суммой также можно отнести большое количество экономических задач. Например, в результате торговых взаимоотношений стран, участвующих в игре, все участники могут оказаться в выигрыше.
Экономические задачи теории игр относятся к обоим типам игр.
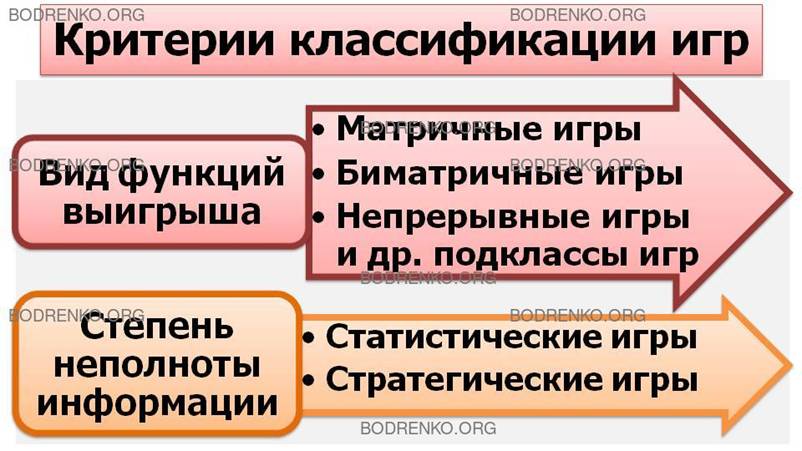
5. Вид функций выигрыша. По этому критерию игры подразделяются на матричные, биматричные, непрерывные, выпуклые, сепарабельные и т.д.
Матричная игра — конечная игра двух игроков с нулевой суммой.
Биматричная игра — конечная игра двух игроков с ненулевой суммой. Выигрыши каждого игрока задаются своей матрицей, в которой строка соответствует стратегии игрока 1, а столбец – стратегии игрока 2. Однако элемент первой матрицы показывает выигрыш игрока 1, а элемент второй матрицы – выигрыш игрока 2. Для биматричных игр так же, как и для матричных, разработана теория оптимального поведения игроков.
Если функция выигрышей каждого игрока в зависимости от стратегий является непрерывной, игра считается непрерывной.
Если функция выигрышей выпуклая, то и игра – выпуклая.
Если функция выигрышей может быть представлена в виде суммы произведений функций одного аргумента, то игра относится к сепарабельной.
6. Степень неполноты информации. По этому критерию игры делятся на статистические и стратегические.
Стратегические игры проходят в условиях полной неопределенности.
Статистические игры проводятся в условиях частичной неопределенности. В статистической игре имеется возможность получения информации на основе статистического эксперимента, по результатам которого оценивается распределение вероятностей стратегий игроков. С теорией статистических игр тесно связана теория принятия экономических решений.
7. Информированность сторон. По этому критерию различают игры с полной и неполной информацией.
Игра определяется как игра с полной информацией, если каждый игрок на каждом ходу игры знает все стратегии, примененные ранее другими игроками на предыдущих ходах.
Если же игроку известны не все стратегии предыдущих ходов других игроков, то игра называется игрой с неполной информацией.
8. Количество ходов. По этому критерию игры делятся на одношаговые или многошаговые. Одношаговые заканчиваются после одного хода каждого игрока, и происходит распределение выигрышей. Многошаговые игры бывают позиционными, стохастическими, дифференциальными и т.д.


1.4. ПОНЯТИЕ МАТРИЧНОЙ ИГРЫ.
В практических ситуациях часто появляется необходимость согласования действий компаний, объединений, министерств и других участников проектов в случаях, когда их интересы не совпадают. В подобных ситуациях теория стратегических игр позволяет найти оптимальное решение для поведения всех участников проектов, обязанных согласовывать действия при столкновении интересов.
Риск и неопределенность исходов игры обусловлены случайным состоянием среды, или выбором образа действия противоположной стороны, или вероятностным характером появления желаемого результата по возможным стратегиям.
В стратегических играх создание модели должно начинаться с построения платежной матрицы. Это наиболее трудоемкий и ответственный этап подготовки принятия решения, так как ошибки в платежной матрице не могут быть компенсированы никакими вычислительными методами и могут привести к неверному итоговому результату.
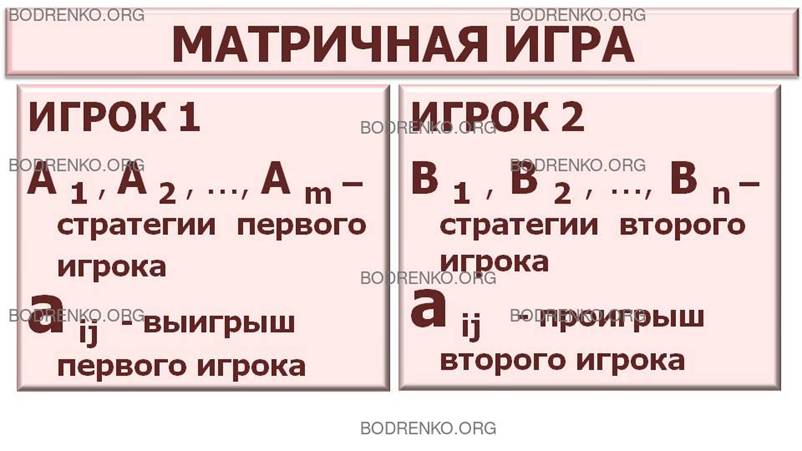
Начнем изучение теории игр с простейшей статической модели — матричной игры, в которой участвуют два игрока, множество стратегий каждого из игроков конечно, а выигрыш одного игрока равен проигрышу другого.
Для того чтобы составить экономико-математическую модель конфликтной ситуации в виде матричной игры, необходимо построить матрицу выигрышей. Это весьма нетривиальная задача особенно для игр большой размерности. В общем виде матрица игры (платежная матрица) строится следующим образом:
1) перечисляем все возможные чистые стратегии Ai и Bj игроков;
2) формализуем правила, по которым развивается конфликт, в виде функции выигрышей
![]()
В общем случае платежная матрица матричной игры является прямоугольной (рис. 1).
|
Игрок 2 Игрок
1 |
B1 |
B2 |
… |
Bn |
|
A1 |
a11 |
a12 |
… |
a1n |
|
A2 |
a21 |
a22 |
… |
a2n |
|
… |
… |
… |
… |
… |
|
Am |
am1 |
am2 |
… |
amn |
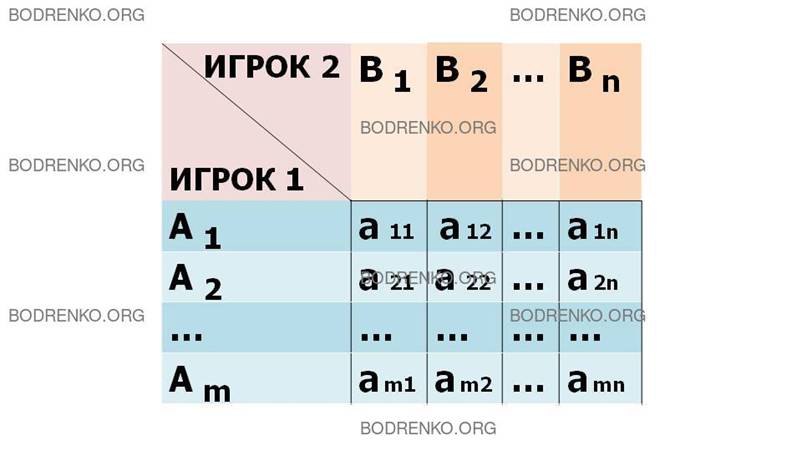
Рис. 1. Платежная матрица.
Номер строки матрицы соответствует номеру стратегии, применяемой игроком 1. Номер столбца соответствует номеру стратегии игрока 2. Выигрыш игрока 1 является элементом матрицы. Выигрыш игрока 2 равен проигрышу игрока 1.
Матричные игры всегда имеют решения в смешанных стратегиях. Они могут быть решены методами линейного программирования.
Пример построения платежной матрицы.
На каждой из двух баз ассортиментный минимум составляет один и тот же набор из n видов товаров. Каждая база должна поставить в свой магазин только одни из этих n видов товаров.
Магазины, назовем их «магазин A» и «магазин B», конкурируют между собой. Один и тот же вид товара продается в обоих магазинах по одной и той же цене. Однако товар, поставляемый в «магазин B», более высокого качества.
Если «магазин A» завезет с базы товар i-го вида, а «магазин B» завезет с базы товар j-го вида, отличный от товара i-го вида (то есть i ≠ j), то товар i-го вида в «магазине A» будет пользоваться спросом, и «магазин A» получит прибыль Ci у.е.
Если же в «магазин A» и «магазин B» завезены товары одинакового вида (то есть i = j), то товар i-го вида в «магазине A» не будет пользоваться спросом, так как такой же товар, но более высокого качества, продается в «магазине B» по такой же цене.
В этом случае (i=j) «магазин A» получит убытки Dj у.е. по транспортировке, хранению и, возможно, порче товара i-го вида в этом магазине.
Требуется составить платежную матрицу игры.
Решение.
Формализуем данную конфликтную ситуацию. Назовем ее игрой «Поставка товаров».
Пусть в качестве Игрока 1 выступает «магазин A», а в качестве Игрока 2 выступает «магазин B».
Игрок 1 с целью достижения прибыли имеет возможность выбрать одну из n стратегий Ai – завезти со своей базы товар i-го вида.
Игрок 2 также имеет возможность выбрать одну из n стратегий Bj – завезти со своей базы товар j-го вида.
Пусть игроки выбрали стратегии {Ai, Bj}.
Тогда можно определить следующую
функцию выигрышей Игрока 1.
![]()
Для каждого фиксированного номера i (i = 1, …, n) имеем:
f(1,j) = C1 при 1 ≠ j, f (1,1) = - D1, j = 1, … n;
f(2,j) = C2 при 2 ≠ j, f (2,2) = - D2, j = 1, … n;
…
f(n,j) = Cn при n ≠ j, f (n,n) = - Dn, j = 1, … n
Платежная матрица (квадратная матрица порядка n) будет иметь следующий вид (рис. 2).
|
Игрок 2 Игрок
1 |
B1 |
B2 |
… |
Bn |
|
A1 |
-D1 |
C1 |
… |
C1 |
|
A2 |
C2 |
-D2 |
… |
C2 |
|
… |
… |
… |
… |
… |
|
An |
Cn |
Cn |
… |
-Dn |
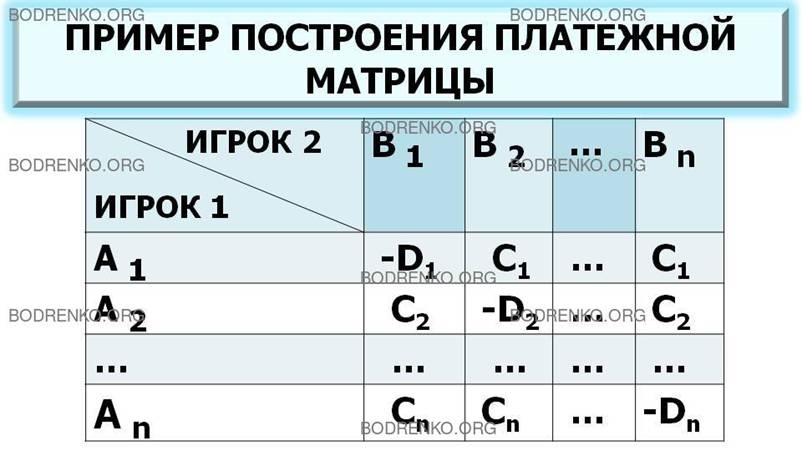
Рис. 2. Платежная матрица игры «Поставка товаров».
2. ИСХОДНАЯ МОДЕЛЬ МАТРИЧНОЙ ИГРЫ. ПОНЯТИЕ НУЛЕВОЙ СУММЫ. ПЛАТЕЖНАЯ МАТРИЦА.
Пусть игрок 1 имеет m стратегий A1, A2, …, Am , а игрок 2 имеет n стратегий B1, B2, …, Bn .
Игра может быть названа «игрой m x n».
Представим матрицу эффективности (платежную матрицу) игры двух лиц с нулевой суммой, сопроводив ее необходимыми обозначениями (рис. 3).
|
Игрок 2 Игрок 1 |
B1 |
B2 |
… |
Bn |
αi |
|
A1 |
a11 |
a12 |
… |
a1n |
α1 |
|
A2 |
a21 |
a22 |
… |
a2n |
α2 |
|
… |
… |
… |
… |
… |
… |
|
Am |
am1 |
am2 |
… |
amn |
αm |
|
β j |
β 1 |
β 2 |
… |
β n |
|
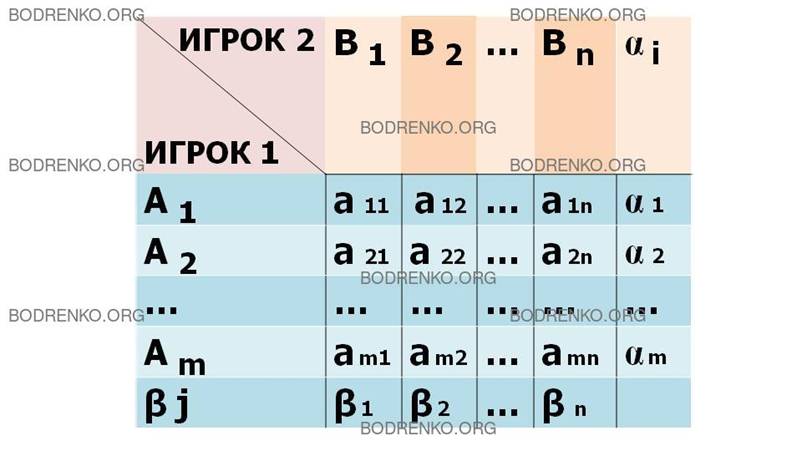
Рис. 3. Платежная матрица игры «m x n».
В данной матрице элементы aij — это значения выигрышей игрока 1, они могут означать и математическое ожидание выигрыша (среднее значение), если выигрыш является случайной величиной.
Величины α1,
α2, …, αm – это минимальные значения элементов a
ij по
строчкам.
Величины β1,
β2, …, βn – это максимальные значения элементов a
ij по столбцам.
![]()
![]()
Их содержательный смысл будет отражен ниже.
Рассмотрим матричную игру, представленную матрицей выигрышей m x n, где число строк равно числу m, а число столбцов равно числу n (рис. 3).
Применим принцип получения максимального гарантированного результата при наихудших условиях.
Игрок 1 стремится принять такую стратегию, которая должна обеспечить максимальный проигрыш игрока 2.
Соответственно игрок 2 стремится принять стратегию, обеспечивающую минимальный выигрыш игрока 1.

Рассмотрим оба этих подхода.
Подход игрока 1. Он должен получить максимальный гарантированный результат при наихудших условиях.
Значит, при выборе отвечающей этим условиям своей чистой i-й стратегии (на рис. 3 этой стратегии соответствует i-я строка выигрышей) он должен выбрать гарантированный результат в наихудших условиях, т.е. наименьшее значение своего выигрыша a ij , которое обозначим αi .
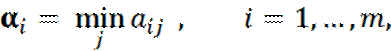
Чтобы этот гарантированный эффект в наихудших условиях был максимальным, нужно из всех αi выбрать наибольшее значение.
Обозначим его α и назовем чистой нижней ценой игры («максимин»):
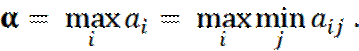
Таким образом, максиминной
стратегии отвечает строка матрицы, которой соответствует элемент α. Какие
бы стратегии ни применял игрок 2, игрок 1 максиминной чистой стратегией
гарантировал себе выигрыш не меньший, чем α.
Таково оптимальное поведение игрока 1.
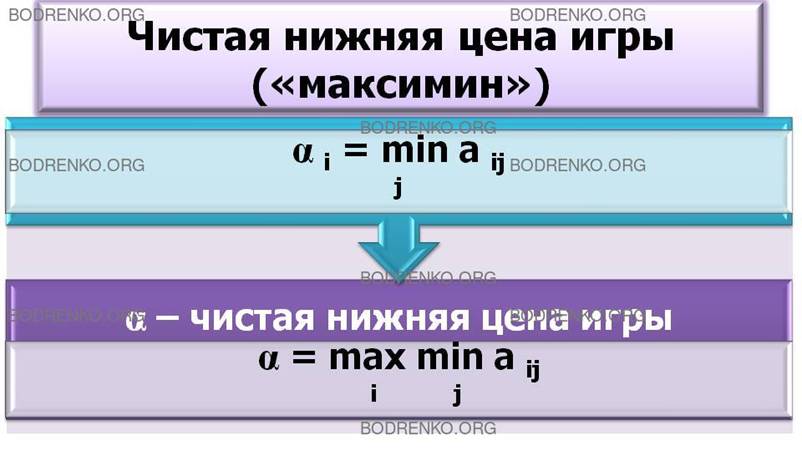
Подход игрока 2. Своими оптимальными стратегиями он стремится уменьшить выигрыш игрока 1, поэтому при каждой j-й чистой стратегии он отыскивает величину своего максимального проигрыша βj в каждом j-м столбце
![]()
То есть игрок 2 определяет максимальный выигрыш игрока 1, если игрок 2 применит j-ю чистую стратегию.
Из всех своих n чистых
стратегий B1, B2, …, Bn игрок 2 отыскивает такую,
при которой игрок 1 получит минимальный выигрыш, то есть игрок 2 определяет ![]() - чистую
верхнюю цену игры («минимакс»):
- чистую
верхнюю цену игры («минимакс»):
![]()
Чистая верхняя цена игры показывает, какой максимальный выигрыш может гарантировать игрок 1, применяя свои чистые стратегии, – выигрыш, не меньший, чем α.
Игрок 2 за счет указанного выше выбора своих чистых стратегий не допустит, чтобы иuрок 1 мог получить выигрыш, больший, чем β. Таким образом, минимаксная стратегия отображается столбцом платежной матрицы, в котором находится элемент β (рис. 3).
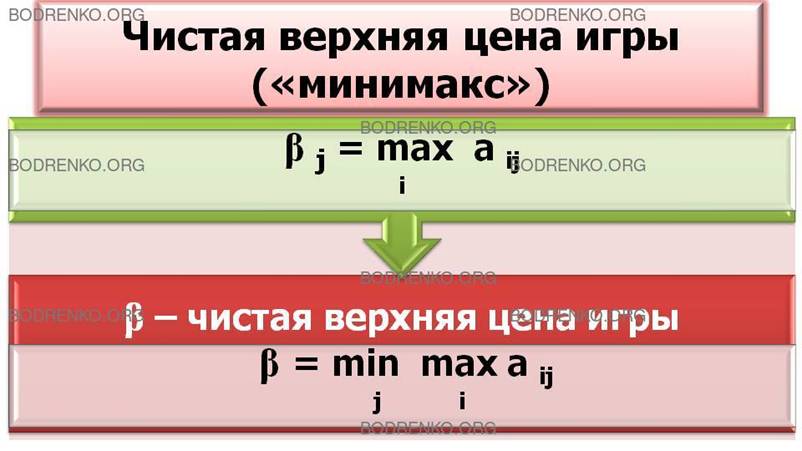
Она является оптимальной чистой гарантирующей стратегией игрока 2, если он ничего не знает о действиях игрока 1.
Чистая цена игры ν есть цена данной игры, если нижняя и верхняя ее цены совпадают, то есть
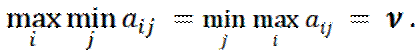
В этом случае игра называется игрой с седловой точкой.
Пример 1. Определить верхнюю и нижнюю цены при заданной матрице игры и указать максиминную и минимаксную стратегии.
Задана матрица игры (рис. 4).
|
Игрок 2 Игрок 1 |
B1 |
B2 |
B3 |
αi |
|
A1 |
2 |
1 |
3 |
1 |
|
A2 |
4 |
5 |
6 |
4 |
|
βj |
4 |
5 |
6 |
|
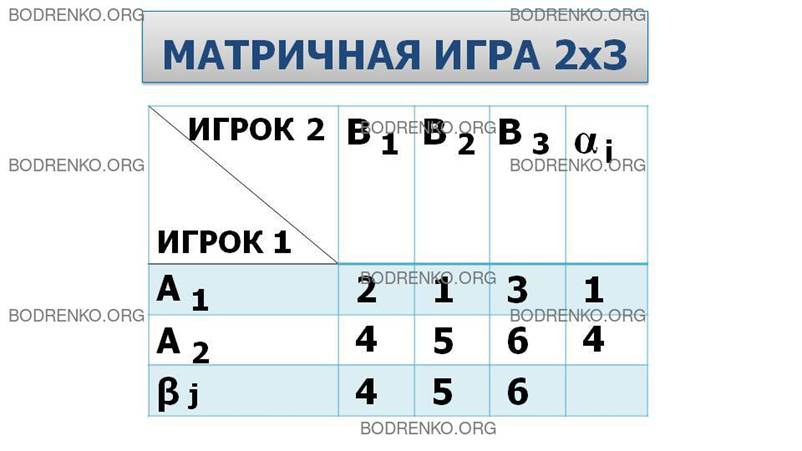
Рис. 4. Матричная игра 2 x 3 с седловой точкой.
Решение. Определим нижнюю цену игры α:
α 1 = 1; α 2 = 4; α = 4 (см. столбец αi).
Определим верхнюю цену игры β:
β 1 = 4; β 2 = 5; β 3 = 6; β = 4 (см. строку βj).
Таким образом, α = β = 4, т.е.
![]()
Значит, α = β = ν = 4 – чистая цена игры при стратегиях А2 и В 1 .
Следовательно, имеем игру с седловой точкой.
Максиминная стратегия игрока 1 – A2, минимаксная стратегия игрока 2 – B1.

Пример 2. Определим максиминную и минимаксную стратегии игроков при заданной платежной матрице (рис. 5).
|
Игрок 2 Игрок 1 |
B1 |
B2 |
B3 |
B4 |
αi |
|
A1 |
2 |
7 |
9 |
10 |
2 |
|
A2 |
8 |
5 |
4 |
6 |
4 |
|
β j |
8 |
7 |
9 |
10 |
|
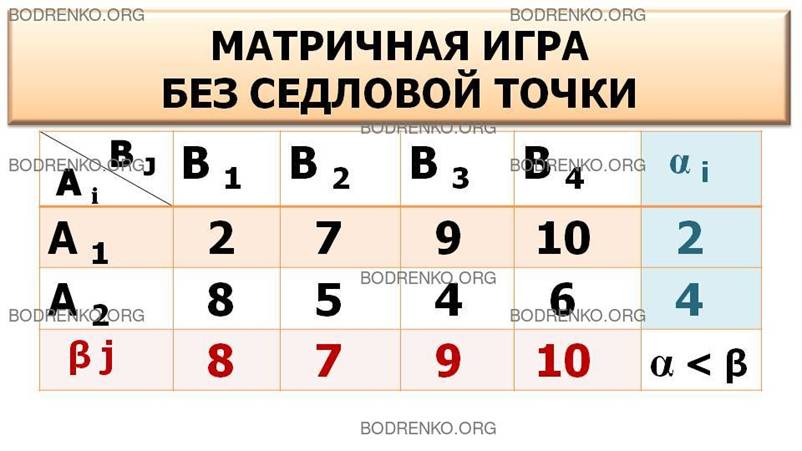
Рис. 5. Матричная игра «2 x 4» без седловой точки.
Решение. Определим максиминную стратегию:
α 1 = 2; α 2 = 4; α = 4 (см. столбец αi).
Максиминная стратегия игрока 1 – А2 .
Определим минимаксную стратегию:
β 1 = 8; β 2 = 7; β 3 = 9; β 4 = 10; β = 7 (см. строку βj).
Минимаксная стратегия игрока 2 – В2 . Здесь α< β, следовательно, седловой точки нет.

3. СТРАТЕГИИ ИГРОКОВ. ВЕРХНЯЯ И НИЖНЯЯ ЦЕНА ИГРЫ. СИТУАЦИИ РАВНОВЕСИЯ (СЕДЛОВЫЕ ТОЧКИ). НАХОЖДЕНИЕ СЕДЛОВЫХ ТОЧЕК.
3.1. ВЫБОР ОПТИМАЛЬНЫХ СТРАТЕГИЙ.
1. В игре с седловой точкой.
Если матрица игры содержит элемент, минимальный в своей строке и максимальный в своем столбце, то он, как уже сказано выше, является седловой точкой. В этом случае мы имеем игру с седловой точкой.
Если в игре с седловой точкой один игрок придерживается седловой точки, тогда другой получит лучший результат, если также будет придерживаться этой точки. Лучшее поведение игрока не должно повлечь уменьшение его выигрыша. Зато худшее поведение может привести к этому. В данном случае решением игры являются:
• чистая стратегия игрока 1;
• чистая стратегия игрока 2;
• седловой элемент.
В данном случае оптимальные чистые стратегии – это чистые стратегии, образующие седловую точку.
2. В игре без седловой точки.
Если игрок 1 информирован о стратегии, принятой игроком 2, он сможет принять оптимальную стратегию, которая не совпадает с максиминной.
Рассмотрим следующий пример.
Пример 3. Дана матрица игры (рис. 6):
|
Игрок 2 Игрок 1 |
B1 |
B2 |
B3 |
B4 |
B5 |
αi |
|
A1 |
7 |
5 |
3 |
6 |
11 |
3 |
|
A2 |
8 |
4 |
6 |
7 |
9 |
4 |
|
β j |
8 |
5 |
6 |
7 |
11 |
|

Рис. 6. Матричная игра «2 x 5» без седловой точки.
Определим минимаксную стратегию игрока 2:
β 1 = 8; β 2 = 5; β 3 = 6; β 4 = 7; β 5 = 11; β = 5 (см. строку βj).
Верхняя цена игры β = 5; минимаксная стратегия игрока 2 – В2 .
Допустим, что игроку 1 стало известно, что игрок 2 принял минимаксную стратегию. Игрок 1 должен выбрать оптимальную стратегию при условии, что В2 – стратегия игрока 2 (β =5).
Решение. Определим максиминную стратегию игрока 1:
α 1 = 3; α 2 = 4; α = 4 (см. столбец αi).
Максиминная стратегия игрока 1 – А2 .
Здесь α< β (4<5), следовательно, седловой точки нет.
Выберем оптимальную стратегию для игрока 1 при условии, что игрок 1 знает, что игрок 2 принял минимаксную стратегию B2.
Ею будет не максиминная А2,
дающая игроку 1 выигрыш α = 4, а та стратегия, которая соответствует
максимальному элементу в столбце В2.
То есть max a
i2 = 5 – это элемент a 12, который
находится в первой строке матрицы - в
строке A1.
В этом случае максимальный гарантированный выигрыш игрока 1 будет равен верхней цене игры β = 5, поэтому игрок 1 выбирает свою оптимальную стратегию А1 , зная, что игрок 2 выбрал свою стратегию В2 .
Таким образом, рассмотренный пример дает результат, отличный от результата при игре с седловой точкой. На примере 3 показано, что бывают ситуации, когда игрок 1 может получить выигрыш, превосходящий максиминный, если ему известны намерения игрока 2.
Стратегия является оптимальной, если ее применение обеспечит игроку наибольший гарантированный выигрыш при любых возможных стратегиях другого игрока. При многократном повторении игры в сходных условиях можно добиться гарантированного среднего выигрыша, превосходящего для игрока 1 максиминный.
3.2. СМЕШАННЫЕ СТРАТЕГИИ.
Рассмотрим теперь подробнее случай, когда в игре отсутствует седловая точка, то есть случай, когда α < β.
Если в матричной игре отсутствует седловая точка в чистых стратегиях, то находят верхнюю и нижнюю цены игры. Они показывают, что игроку 1 гарантирован выигрыш, не меньший нижней цены игры α. А игрок 2 может обеспечить себе проигрыш, не больший β, то есть игрок 1 не получит выигрыша, превосходящего верхнюю цену игры β.
В примере 3 игрок 1 получил при своей оптимальной стратегии А1, отличной от максиминной, выигрыш, равный верхней цене игры β = 5. Такова плата за информированность о стратегии игрока 2. Это крайний случай.
Не улучшится ли результат игрока 1, если информация о действиях противной стороны будет отсутствовать, но игрок будет многократно применять чистые стратегии случайным образом с определенной вероятностью?
Возникает вопрос, как «справедливо» разделить разность (β – α > 0) между игроками?
Оказывается, что компромиссного распределения разности (β – α) между игроками можно добиться путем случайного чередования игроками чистых стратегий.
При этом игрок 1 может получать выигрыши, в среднем большие нижней цены игры α, но меньшие верхней цены игры β.
Для этого применяют смешанные стратегии, которые можно представить в виде случайных величин, возможными значениями которых являются чистые стратегии.
Пусть для игрока 1 смешанная стратегия S1 заключается в применении чистых стратегий А1, А2,..., Аm с соответствующими вероятностями р1, р2, ..., pm:
![]()
где
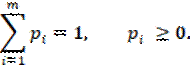
Число ![]() – это
вероятность того, что игрок 1 применит чистую стратегию
– это
вероятность того, что игрок 1 применит чистую стратегию ![]()

Для игрока 2 смешанная стратегия S2 заключается в применении чистых стратегий B1, B2, … Bn с вероятностями q1, q2, …, qn:
![]()
где
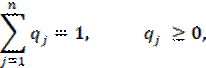

Число ![]() – это вероятность того, что игрок 2 применит
чистую стратегию
– это вероятность того, что игрок 2 применит
чистую стратегию ![]() .
.
В случае, когда pi = 1 , для игрока 1 имеем чистую стратегию:
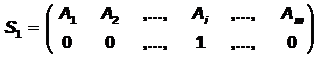
Если мы окажемся в
ситуации {Ai, Bj}, то есть когда игрок 1
применит стратегию Ai,
а игрок 2 при этом применит стратегию Bj, то она реализуется с вероятностью
![]() .
.
В матричной игре, зная платежную матрицу A (она относится и к игроку 1, и к игроку 2), можно определить средний выигрыш игрока 1:
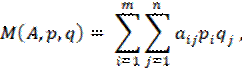
где p, q – векторы с компонентами pi, qj, соответственно.
Стратегии ![]() и
и ![]()
называются оптимальными смешанными стратегиями игроков, если выполнено следующее условие оптимальности:
![]() (*)
(*)

Поясним полученные соотношения.
Левая часть этого неравенства
![]()
означает, что если первый игрок отклоняется от оптимальной стратегии p0, то его выигрыш может только уменьшиться при условии, что второй игрок придерживается оптимальной стратегии q0.
Аналогично, неравенство
![]()
означает, что если второй игрок отклоняется от оптимальной стратегии q0, то его проигрыш может только увеличиться.
Условие оптимальности (*) аналогично условию:
![]()
Величина
![]()
называется ценой игры
Решить игру означает найти
цену игры и оптимальные стратегии. То есть решением игры является нахождение «набора»
(![]()
Естественно, что возникают следующие вопросы.
Какие матричные игры имеют решение в смешанных стратегиях и как найти это решение, если оно существует?
Ответ на этот вопрос дает основная теорема теории матричных игр.
Теорема (Неймана).
Для матричной игры с любой матрицей A величины
![]()
![]()
существуют и равны между собой:
![]()
Более того, существует, по крайней мере, одна ситуация
![]() ),
для которой выполняется соотношение:
),
для которой выполняется соотношение:
![]()


Другими словами, любая матричная игра имеет решение в смешанных стратегиях.
В состав оптимальных смешанных стратегий игроков могут входить не все чистые стратегии
Ai, B j. То
есть вероятности некоторых из них будут равны нулю: ![]() ,
, ![]()
Значит, не все заданные чистые стратегии игроков будут входить априори в их оптимальные смешанные стратегии.
Тогда те чистые стратегии, которые входят в оптимальные смешанные стратегии, называются активными чистыми стратегиями.
Справедлива следующая теорема.
Теорема.
Оптимальная смешанная стратегия p0
первого игрока смешивается только из тех чистых стратегий Ai, ![]() , для которых справедливы равенства:
, для которых справедливы равенства:
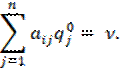
А
в оптимальной смешанной стратегии q0 второго игрока смешиваются только те стратегии Bj, ![]() ,
для которых справедливы равенства:
,
для которых справедливы равенства:
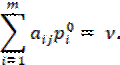


Перечислим условия
применения смешанных стратегий:
1.
Игра без седловой точки;
2.
Игроки используют случайную смесь чистых
стратегий с заданными вероятностями;
3.
Игра многократно повторяется в сходных условиях;
4.
При любом ходе ни один из игроков не
информирован о стратегии другого игрока;
5.
Допускается усреднение результатов игр.

3.3. ОПТИМАЛЬНЫЕ СМЕШАННЫЕ СТРАТЕГИИ В МАТРИЧНОЙ ИГРЕ 2x2
Рассмотрение методов нахождения оптимальных смешанных стратегий для матричных игр начнем с простейшей игры, описываемой матрицей 2х2.
При отсутствии седловой точки можно получить две оптимальные смешанные стратегии. Как уже отмечалось, эти смешанные стратегии записываются так:
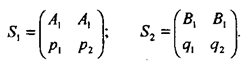
Значит, имеется платежная матрица
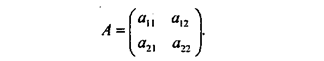
При этом
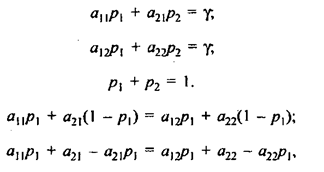
откуда получаем оптимальные значения ![]() и
и ![]() :
:
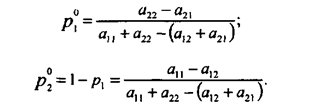

Зная ![]() и
и ![]() находим g:
находим g:
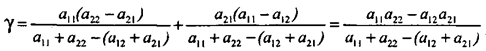
Вычислив g, находим ![]() и
и ![]() :
:
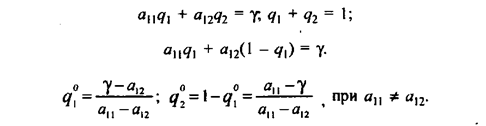

Задача решена, так как найдены векторы
и цена игры g.
3.4.
МАЖОРИРОВАНИЕ (ДОМИНИРОВАНИЕ) СТРАТЕГИЙ
Мажорирование представляет отношение между стратегиями, наличие которого во многих практических случаях дает возможность сократить размеры исходной платежной матрицы игры. Рассмотрим это понятие на примере матрицы
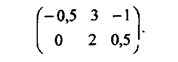
Рассуждая с позиции игрока 2, можно обнаружить преимущество его третьей стратегии перед второй, поскольку при первой стратегии игрока 1 выигрыш игрока 2 равен —3 (вторая стратегия) и 1 (третья стратегия), а при второй стратегии игрока 1 выигрыш игрока 2 равен —2 (вторая стратегия) и - 0,5 (третья стратегия).
Таким образом, при любой стратегии игрока 1 игроку 2 выгоднее применять свою третью стратегию по сравнению со второй; при наличии третьей стратегии игрок 2, если он стремится играть оптимально, никогда не будет использовать свою вторую стратегию, поэтому ее можно исключить из игры, т.е. в исходной платежной матрице можно вычеркнуть 2-й столбец:
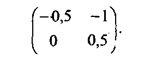
С позиции игрока 1 его первая стратегия
оказывается хуже второй, так как по первой стратегии он только проигрывает.
Поэтому первую стратегию можно исключить, а матрицу игры преобразовать к виду:
(0 0,5).
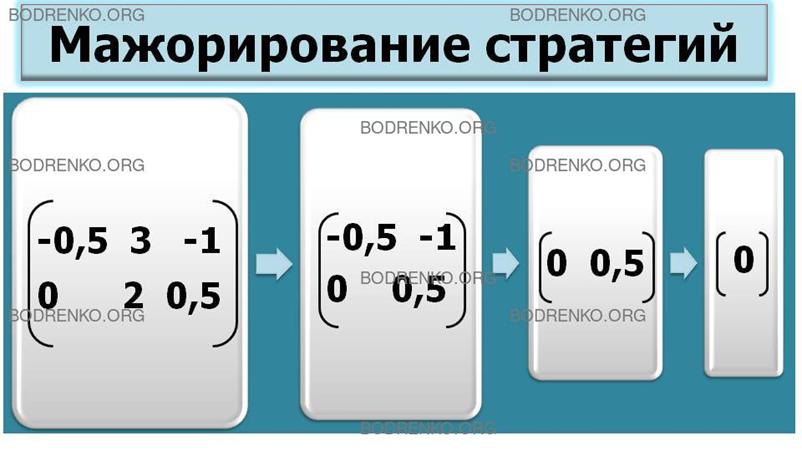
Учитывая интересы игрока 2, следует оставить только его первую стратегию, поскольку, выбирая вторую стратегию, игрок 2 оказывается в проигрыше (0,5 - выигрыш игрока 1), и матрица игры принимает простейший вид: (0), т.е. имеется седловая точка.
Мажорирование можно распространить и на смешанные стратегии. Если элементы одной строки не все меньше (или равны) соответствующих элементов других строк, но все меньше (или равны) некоторых выпуклых линейных комбинаций соответствующих элементов других строк, то эту стратегию можно исключить, заменив ее смешанной стратегией с соответствующими частотами использования чистых стратегий.
В качестве иллюстрации к сказанному рассмотрим матрицу игры:
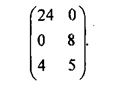
Для первых двух чистых стратегий игрока 1 возьмем частоты их применения (вероятности) равными 0,25 и 0,75.
Третья стратегия игрока 1 мажорируется линейной выпуклой комбинацией первой и второй чистых стратегий, взятых с частотами 0,25 и 0,75 соответственно, т.е. смешанной стратегией:
24*0,25 + 0*0,75 = 6 > 4;
0*0,25 + 8*0,75 = 6 > 5.
Поэтому третью стратегию игрока 1 можно исключить, используя вместо нее указанную выше смешанную стратегию.

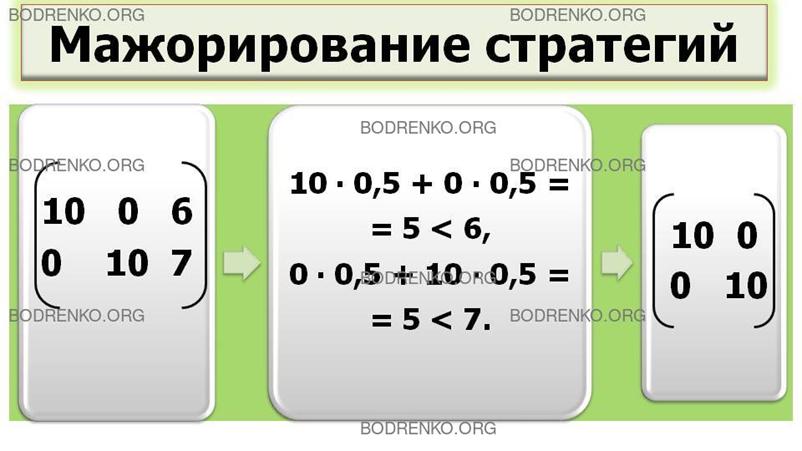
Аналогично если каждый элемент некоторого столбца больше или равен некоторой выпуклой линейной комбинации соответствующих элементов некоторых других столбцов, то этот столбец можно исключить из рассмотрения (вычеркнуть из матрицы). Например, для матрицы
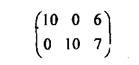
третья стратегия игрока 2 мажорируется смешанной стратегией из первой и второй его чистых стратегий, взятых с частотами 0,5 и 0,5:
10*0,5 + 0*0,5 = 5 < 6;
0*0,5 + 10*0,5 = 5 < 7.
Таким образом, исходная матрица игры эквивалентна матрице следующего вида:
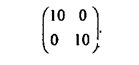
Как видно, возможности мажорирования смешанными стратегиями в отличие от чистых значительно менее прозрачны (нужно должным образом подобрать частоты применения чистых стратегий), но такие возможности есть, и ими полезно уметь пользоваться.
Список рекомендуемой литературы.
1. Данилов В.И. Лекции по теории игр. М.: Российская экономическая школа, 2001.
2. Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых ситуаций в экономике и бизнесе.

3. Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс. Учебное пособие. СПб.: 2001.
4. Шапкин А.С., Шапкин В.А. Теория риска и моделирование рисковых ситуаций. Учебник. М.: 2005.
5. Петросян Л.А., Зенкевич Н.А., Шевкопляс Е.В. Теория игр. Учебник. 2012.
